Angulos y distancias

Distancia entre dos puntos

$d = \sqrt{{(x_{2} - x_{1})}^{2} + {(y_{2} - y_{1})}^{2} + {(z_{2} - z_{1})}^{2}}$

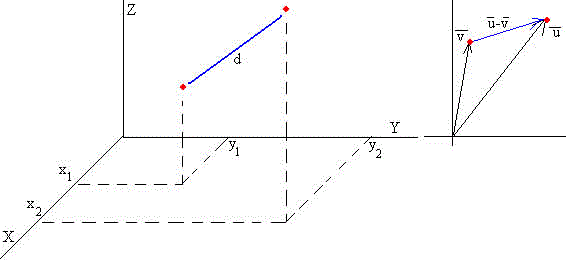
Calcular la distancia entre los puntos A (1,2,3) y B (4,-1,3)

La distancia entre dos puntos es el módulo del vector diferencia de los vectores $\vec{u} - \vec{v}$

>> u=[1,2,3];
>> v=[4,-1,3];
>> norm(u-v)
ans =    4.2426

Vector normal a un plano

Primero calculamos la ecuación del plano que pasa por un punto A y es perpendicular a un vector $\vec{n}$ tal como se muestra en la figura. El vector $\vec{u}$ va del punto A(x₀,y₀,z₀) al punto P(x,y,z)

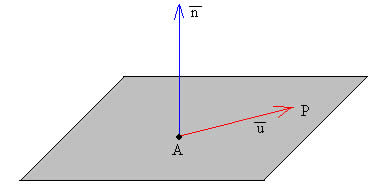
El producto escalar de los vectores $\vec{n}$ y $\vec{u}$ deberá ser cero.

$\begin{array}{l} \vec{u} = (x - x_{0}) \hat{i} + (y - y_{0}) \hat{j} + (z - z_{0}) \hat{k} \\ \vec{n} = a \hat{i} + b \hat{j} + c \hat{k} \\ \vec{u} \cdot \vec{n} = a (x - x_{0}) + b (y - y_{0}) + c (z - z_{0}) = 0 \\ a x + b y + c z = d \end{array}$

que es la ecuación del plano. Las componentes del vector $\vec{n}$ normal al plano son los coeficientes a, b, c de x, y y z en la ecuación del plano. El vector unitario normal al plano es

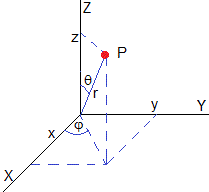
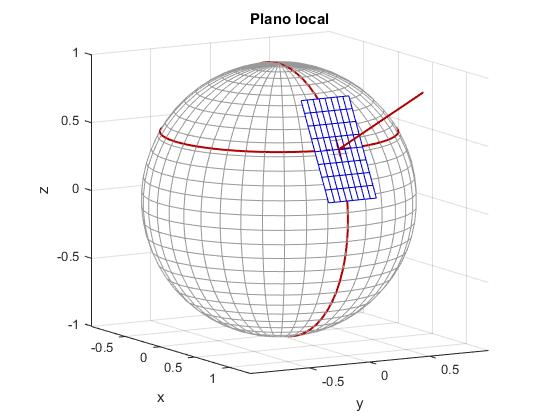
$\hat{n} = \frac{a}{\sqrt{a^{2} + b^{2} + c^{2}}} \hat{i} + \frac{b}{\sqrt{a^{2} + b^{2} + c^{2}}} \hat{j} + \frac{c}{\sqrt{a^{2} + b^{2} + c^{2}}} \hat{k}$

Queremos trazar el plano local, tangente a la superficie esférica de radio r en un punto de coordenadas φ (longitud) y θ (la latitud es λ=π/2-θ)

Las coordenadas del punto P son

${\begin{cases} x_{0} = r \sin θ \cos φ \\ y_{0} = r \sin θ \sin φ \\ z_{0} = r \cos θ \end{cases}$

La dirección del vector $\vec{n}$ perpendicular al plano tangente a la superficie esférica es radial, la recta que pasa por O y P

$\vec{n} = x_{0} \hat{i} + y_{0} \hat{j} + z_{0} \hat{k}$

Para determinar la ecuación del plano multiplicamos escalarmente $\vec{n} \cdot \vec{u}$

$\begin{array}{l} \vec{u} = (x - x_{0}) \hat{i} + (y - y_{0}) \hat{j} + (z - z_{0}) \hat{k} \\ \vec{n} \cdot \vec{u} = (x - x_{0}) x_{0} + (y - y_{0}) y_{0} + (z - z_{0}) z_{0} = 0 \\ x x_{0} + y y_{0} + z z_{0} = r^{2} \end{array}$

%esfera
R=1;
phi=linspace(0,pi,30);
theta=linspace(0,2*pi,40);
[phi,theta]=meshgrid(phi,theta);
x=R*sin(phi).*cos(theta);
y=R*sin(phi).*sin(theta);
z=R*cos(phi);
h1=mesh(x,y,z);
set(h1,'EdgeColor',[0.6,0.6,0.6]);
axis equal

%paralelo
theta=pi/3;
phi=0:0.1:2*pi;
x=sin(theta)*cos(phi);
y=sin(theta)*sin(phi);
z=cos(theta)*ones(1,length(x));
h1=line(x,y,z);
set(h1,'Color',[.7,0,0],'LineWidth',1.5)
%meridiano
phi=0;
theta=-pi:0.1:pi;
x=sin(theta)*cos(phi);
y=sin(theta)*sin(phi);
z=cos(theta);
h1=line(x,y,z);
set(h1,'Color',[.7,0,0],'LineWidth',1.5)

%plano tangente
phi=0;
theta=pi/3;
x0=sin(theta)*cos(phi);
y0=sin(theta)*sin(phi);
z0=cos(theta);
[x,y]=meshgrid(-0.2+x0:0.05:0.2+x0,-0.2+y0:0.05:0.2+y0);
z=(1-x*x0-y*y0)/z0;
hold on
h1=mesh(x,y,z);
set(h1,'EdgeColor',[0,0,0.8])
%normal al plano (dirección radial)
h1=quiver3(x0,y0,z0,0.5,0.5,0.5);
set(h1,'Color',[.7,0,0],'LineWidth',1.5)

axis equal
view(60,10)
hold off
xlabel('x'); ylabel('y'); zlabel('z')
title('Plano local')

Angulo entre dos planos

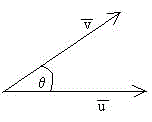
El producto escalar nos permite determinar el ángulo entre dos vectores $\vec{u}$ y $\vec{v}$ .

$\begin{array}{l} \vec{u} \cdot \vec{v} = u \cdot v \cdot \cos θ \\ \vec{u} \cdot \vec{v} = u_{x} v_{x} + u_{y} v_{y} + u_{z} v_{z} \\ \cos θ = \frac{\vec{u} \cdot \vec{v}}{u \cdot v} \end{array}$

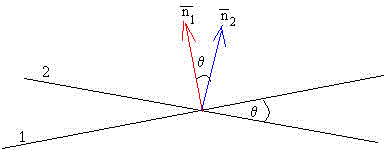
Si $\vec{n_{1}}$ y $\vec{n_{2}}$ son los vectores perpendiculares a cada uno de los dos planos, el ángulo θ entre estos dos vectores es el mismo que el ángulo entre los dos planos. El ángulo entre los dos planos se calcula mediante la siguiente fórmula

$\begin{array}{l} a_{1} x + b_{1} y + c_{1} z = d_{1} \vec{n_{1}} = a_{1} \hat{i} + b_{1} \hat{j} + c_{1} \hat{k} \\ a_{2} x + b_{2} y + c_{2} z = d_{2} \vec{n_{2}} = a_{2} \hat{i} + b_{2} \hat{j} + c_{2} \hat{k} \\ \cos θ = | \frac{\vec{n_{1}} \cdot \vec{n_{2}}}{n_{1} \cdot n_{2}} | \end{array}$

Calcular el ángulo determinado por los planos: x+2y-z=0, x-y+z=3.

>> n1=[1,2,-1];
>> n2=[1,-1,1];
>> coseno=abs(dot(n1,n2)/(norm(n1)*norm(n2)));
>> ang=acosd(coseno)
ang =   61.8745

Angulo entre una recta y un plano

Sea $\vec{n}$ un vector perpendicular al plano y sea $\vec{u}$ un vector cuya dirección es la recta. El ángulo entre el plano y la recta es el complementario al ángulo entre los vectores $\vec{n}$ y $\vec{u}$ .

$\begin{array}{l} a x + b y + c z = d \vec{n} = a \hat{i} + b \hat{j} + c \hat{k} \\ {\begin{cases} x = x_{0} + t u_{x} \\ y = y_{0} + t u_{y} \\ z = z_{0} + t u_{z} \end{cases} \\ \cos (\frac{π}{2} - θ) = | \frac{\vec{n} \cdot \vec{u}}{n \cdot u} | \end{array}$

Calcular el ángulo entre le plano x+y+z=0, y la recta: x=1+t, y=1+2t, z=1+4t.

>> n=[1,1,1];
>> u=[1,2,4];
>> coseno=abs(dot(n,u)/(norm(n)*norm(u)))
coseno =    0.8819
>> ang=90-acosd(coseno)
ang =   61.8745

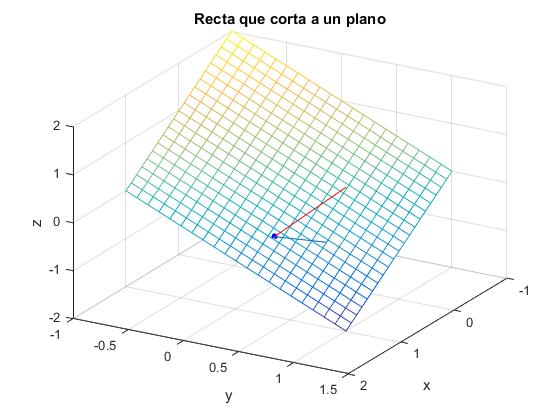
Calculamos la intersección entre el plano y la recta, de ecuaciones

$\begin{array}{l} x + y + z = 0 \\ {\begin{cases} 2 x - y = 1 \\ 4 x - z = 3 \end{cases} \end{array}$

En la figura, vemos el plano, la recta en color rojo, el vector perpendicular al plano en color azul y el punto de intersección de coordendas x=0.5714, y=0.1429, z=-0.7143.

%plano
[x,y] = meshgrid(-1:0.1:1);
z = -x-y;
hold on
mesh(x,y,z)
%recta
x=[0.5,1];
y=2*x-1;
z=4*x-3;
line(x,y,z,'color','r')
%punto de intersección
B=[1,1,1;2,-1,0;4,0,-1];
b=[0;1;3];
X=B\b
plot3(X(1),X(2),X(3),'bo','markersize',4,'markerfacecolor','b');

quiver3(X(1),X(2),X(3),1,1,1) %vector normal al plano
xlabel('x')
ylabel('y')
zlabel('z')
title('Recta que corta a un plano')
grid on
hold off
view(120,30)

Distancia de un punto a un plano

Distancia de un plano al origen

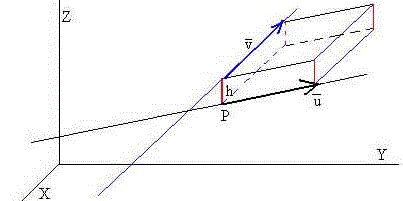
Queremos calcular la distancia h del origen O al plano de ecuación ax+by+cz=d. Tomemos un punto P (x,y,z) del plano,

La distancia h del origen al plano (segmento en color rojo) es la proyección del vector $\vec{u} = x \hat{i} + y \hat{j} + z \hat{k}$ a lo largo de la dirección del vector unitario $\vec{n}$ normal al plano, tal como apreciamos en la figura

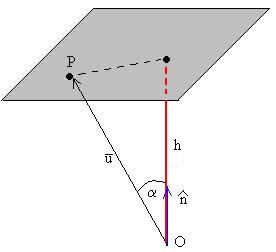
$h = \hat{n} \cdot \vec{u} = \frac{a}{\sqrt{a^{2} + b^{2} + c^{2}}} x + \frac{b}{\sqrt{a^{2} + b^{2} + c^{2}}} y + \frac{c}{\sqrt{a^{2} + b^{2} + c^{2}}} z = \frac{d}{\sqrt{a^{2} + b^{2} + c^{2}}}$

Distancia de un punto a un plano

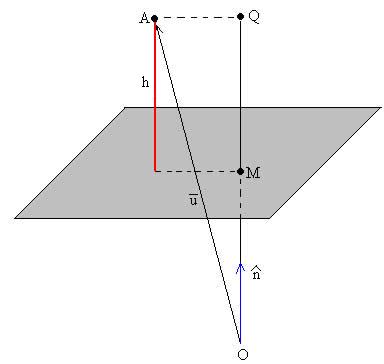
La distancia h del punto A (x₁,y₁,z₁) al plano de ecuación ax+by+cz=d (segmento en color rojo), es la diferencia entre la proyección del vector $\vec{u}$ a lo largo de la dirección $\vec{n}$ (segmento OQ) y la distancia del origen a dicho plano, (segmento OM). h=|OQ|-|OM|

$\begin{array}{l} h = \hat{n} \cdot \vec{u} - d = \frac{a}{\sqrt{a^{2} + b^{2} + c^{2}}} x_{1} + \frac{b}{\sqrt{a^{2} + b^{2} + c^{2}}} y_{1} + \frac{c}{\sqrt{a^{2} + b^{2} + c^{2}}} z_{1} - \frac{d}{\sqrt{a^{2} + b^{2} + c^{2}}} = \\ \frac{a x_{1} + b y_{1} + c z_{1} - d}{\sqrt{a^{2} + b^{2} + c^{2}}} \end{array}$

Calcular la distancia h del punto A (1,3,-2) al plano x-y+z=1

>> n=[1,-1,1];
>> u=[1,3,-2];
>> d=1;
>> h=abs((dot(n,u)-d)/norm(n))
h =    2.8868

Utilizando variables simbólicas

>> n=sym('[1,-1,1]');
>> u=sym('[1,3,-2]');
>> d=sym('1');
>> h=abs((dot(n,u)-d)/sqrt(dot(n,n)))
h =(5*3^(1/2))/3

El módulo de un vector que se calcula con la función norm no funciona con variables simbólicas, se utiliza la operación equivalente: la raíz cuadrada sqrt del producto escalar dot de un vector consigo mismo.

Distancia de un punto a una recta

Queremos calcular la distancia h desde el punto A (x₁,y₁,z₁) a la recta. Sea $\vec{u}$ un vector cuya dirección es la la recta y $\vec{v}$ el vector con origen en un punto P (x₀,y₀,z₀) de la recta y extremo en el punto A.

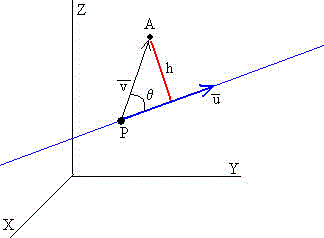
$\begin{array}{l} \vec{v} = (x_{1} - x_{0}) \hat{i} + (y_{1} - y_{0}) \hat{j} + (z_{1} - z_{0}) \hat{k} \\ h = v \cdot \sin θ = \frac{| \vec{u} \times \vec{v} |}{u} \end{array}$

Calcular la distancia entre el punto A (1,2,3) y la recta

${\begin{cases} x = 1 + 2 t \\ y = 1 + 3 t \\ z = 4 + 5 t \end{cases}$

$\begin{array}{l} \vec{u} = 2 \hat{i} + 3 \hat{j} + 5 \hat{k} \\ \vec{v} = (1 - 1) \hat{i} + (2 - 1) \hat{j} + (3 - 4) \hat{k} = \hat{j} - \hat{k} \end{array}$

>> u=[2,3,5];
>> v=[0,1,-1];
>> h=norm(cross(u,v))/norm(u)
h =    1.3765

Utilizando variables simbólicas

>> u=sym('[2,3,5]');
>> v=sym('[0,1,-1]');
>> u_v=cross(u,v);
>> h=sqrt(dot(u_v,u_v)/dot(u,u)) 
h =(6*19^(1/2))/19

Distancia entre dos rectas que se cruzan

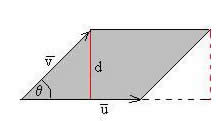
En la figura se muestra cómo se calcula un área a partir del módulo del producto vectorial de los vectores $\vec{u}$ y $\vec{v}$ .

$u \cdot d = u \cdot v \cdot \sin θ = | \vec{u} \times \vec{v} |$

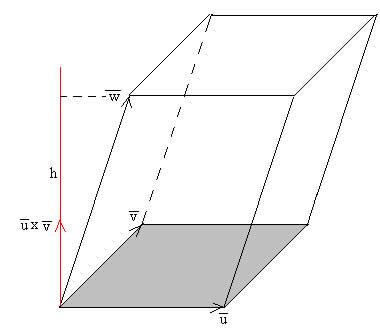
El volumen de un paralepípedo formado por tres vectores $\vec{u}$ , $\vec{v}$ y $\vec{w}$ , es igual al área de la base $| \vec{u} \times \vec{v} |$ por la altura h=w·cosθ. El módulo del producto mixto $(\vec{u} \times \vec{v}) \cdot \vec{w}$ .

Si r₁ y r₂ son dos rectas que se cruzan. Denominamos $\vec{w}$ al vector de origen P (x₁,y₁,z₁) en la recta r₁ y extremo Q (x₂,y₂,z₂) en la recta r₂. El volumen del paralepípedo formado por los vectores $\vec{u}$ , $\vec{v}$ y $\vec{w}$ es el módulo del producto mixto $(\vec{u} \times \vec{v}) \cdot \vec{w}$ . Por otra parte, el volumen del paralepípedo es igual al producto del área de la base $| \vec{u} \times \vec{v} |$ por la altura h que es la distancia entre las dos rectas que se cruzan.

Calcular la distancia h entre las rectas que se cruzan

$r_{1} {\begin{cases} x = 1 + 2 t \\ y = 2 + 3 t \\ z = 1 + 2 t \end{cases} r_{2} {\begin{cases} x = 2 + t \\ y = 2 + 2 t \\ z = 2 + 3 t \end{cases}$

Comprobamos que se cruzan

$r_{1} {\begin{cases} 3 x - 2 y = - 1 \\ x - z = 0 \end{cases} r_{2} {\begin{cases} 2 x - y = 2 \\ 3 x - z = 4 \end{cases}$

>> A=[3,-2,0;1,0,-1;2,-1,0;3,0,-1];
>> b=[-1;0;2;4];
>> Ab=[A b];
>> rank(A)
ans =     3
>> rank(Ab)
ans =     4

Definimos los vectores.

$\vec{u} = 2 \hat{i} + 3 \hat{j} + 2 \hat{k}$ , de la recta r₁

$\vec{v} = \hat{i} + 2 \hat{j} + 3 \hat{k}$ , de la recta r₂

El punto P de la recta r₁ es (1,2,1). El punto Q de la recta r₂ es (2,2,2). El vector $\vec{w}$ de origen P y extremo Q es

$\begin{array}{l} \vec{w} = \hat{i} + \hat{k} \\ h = \frac{| (\vec{u} \times \vec{v}) \cdot \vec{w} |}{| \vec{u} \times \vec{v} |} \end{array}$

>> u=[2,3,2];
>> v=[1,2,3];
>> w=[1,0,1];
>> h=abs(dot(w,cross(u,v)))/norm(cross(u,v))
h =    0.9258

Utilizando variables simbólicas

>> u=sym('[2,3,2]');
>> v=sym('[1,2,3]');
>> w=sym('[1,0,1]');
>> u_v=cross(u,v);
>> h=abs(dot(w,u_v))/sqrt(dot(u_v,u_v))
h =42^(1/2)/7

Referencias

Joaquín Arregui Fernández, Javier Lafuente López, Isabel Morales González, Francisco Padilla Garvi. Matemáticas. Curso de Orientación Universitaria. Editorial Magisterio Español S.A. (1978)