Usamos una jeringa de forma cilíndrica, de radio 1 cm y de longitud 20 cm, para producir la burbuja

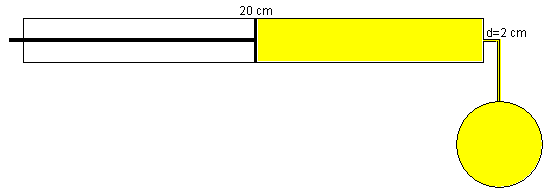
Al empujar el émbolo hasta el final de su recorrido se forma una pompa cuyo radio r₀ es

${\displaystyle \pi ·1^2·20=\frac{4}{3}\pi ·r_0^3}$

donde r₀=2.47 cm.

Fluido no viscoso

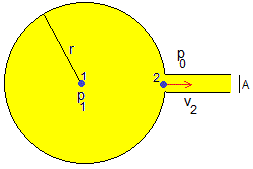
El aire escapa por el tubo horizontal de sección A, el flujo (volumen en la unidad de tiempo) es Av₂, en consecuencia, el radio r de la burbuja disminuye

${\displaystyle \begin{array}{l}-\frac{d}{dt}\left(\frac{4}{3}\pi r^3\right)=A{v}_2\\ 4\pi r^2\frac{dr}{dt}+A{v}_2=0\end{array}}$

Aplicamos la ecuación de Bernoulli en el estado estacionario. p₀ es la presión atmosférica y p₁ la presión en el interior de la burbuja

${\displaystyle p_1=p_0+\frac{1}{2}\rho v_2^2}$

La ecuación de Young-Laplace nos da la presión en el interior de la burbuja

${\displaystyle p_1-p_0=\frac{4\gamma }{r}}$

Despejamos la velocidad de salida v₂

${\displaystyle \begin{array}{l}\frac{4\gamma }{r}=\frac{1}{2}\rho v_2^2\\ v_2=2\sqrt{\frac{2\gamma }{r\rho }}\end{array}}$

Resolvemos la ecuación diferencial en r, separando las variables, con la condición inicial, en el instante t=0, el radio de la burbuja es r₀

${\displaystyle \begin{array}{l}4\pi r^2\frac{dr}{dt}+2A\sqrt{\frac{2\gamma }{r\rho }}=0\\ r^{5/2}dr=-\frac{A}{\pi }\sqrt{\frac{\gamma }{2\rho }}dt\\ {\displaystyle \underset{r_0}{\overset{r}{\int }}{r}^{5/2}dr}=-\frac{A}{\pi }\sqrt{\frac{\gamma }{2\rho }}{\displaystyle \underset{0}{\overset{t}{\int }}dt}\\ r^{7/2}=r_0^{7/2}-\frac{7A}{2\pi }\sqrt{\frac{\gamma }{2\rho }}t\end{array}}$

Fluido viscoso

Se conecta la burbuja al extremo del tubo capilar de longitud L y radio R. El aire que circula por el tubo se comporta como un fluido viscoso, aplicamos la ley de Poiseuille suponiendo que el aire fluye en régimen laminar.

${\displaystyle G=\frac{\pi }{8}\frac{\Delta p·R^4}{\eta L}}$

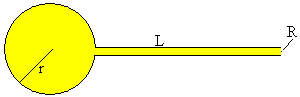
donde G es el gasto o volumen de fluido que fluye en la unidad de tiempo, Δp es la diferencia de presión entre los extremos del tubo, y η es la viscosidad del fluido.

La fórmula de Young-Laplace nos da el valor de la diferencia de presión entre el interior y el exterior de la burbuja, o entre los extremos del tubo capilar, Δp=4γ/r

El volumen de la burbuja disminuye con el tiempo al escaparse el aire por el tubo capilar, G=-dV/dt.

La ecuación que nos describe la variación del radio r de la burbuja con el tiempo será

${\displaystyle \begin{array}{l}-\frac{dV}{dt}=\frac{\pi }{8}\frac{4\gamma }{r}\frac{R^4}{\eta L}\\ r\left(\frac{dV}{dr}\right)dr=-\frac{\pi \gamma R^4}{2\eta L}dt\\ {\displaystyle \underset{r_0}{\overset{r}{\int }}r\left(\frac{dV}{dr}\right)dr=}-\frac{\pi \gamma R^4}{2\eta L}t\end{array}}$

Esta es la ecuación que emplearemos en el siguiente apartado para establecer la relación entre le radio r de la burbuja y el tiempo t, con diferentes expresiones para el volumen V en función de r

Aproximación

El caso más simple, consiste en considerar que la burbuja mantiene su forma aproximadamente esférica a medida que se desinfla. Esto es cierto, si el radio del tubo es muy pequeño frente al radio de la burbuja. Para una burbuja de forma esférica de radio r, el volumen V=4πr³/3.

En el instante t=0, el radio de la pompa de jabón es r₀, y en el tiempo t es r. Integrando entre estos límites se obtiene.

${\displaystyle r^4-r_0^4=-\frac{\gamma R^4}{2\eta L}t}$

El tiempo t que tarda en desaparecer la burbuja, r=0 es

${\displaystyle t=\frac{2\eta L}{\gamma }{\left(\frac{r_0}{R}\right)}^4}$

A partir de la medida del tiempo t, se despeja la tensión superficial γ de la solución jabonosa.

Ejemplo

Determinar la tensión superficial de una solución jabonosa, sabiendo que el tiempo que tarda en desaparecer una burbuja de radio r₀=2.47 cm es de t=57.8 s. El capilar empleado tiene un radio R=0.1 cm y una longitud de L=10 cm.

Dato, la viscosidad del aire es de η =1.72·10^-5 kg/(m·s).

${\displaystyle 57.8=\frac{2·1.72·{10}^{-5}·0.1}{\gamma }{\left(\frac{2.47}{0.1}\right)}^4\gamma =0.022\text{N/m}}$

Modelo de evolución de la burbuja

En al figura, se muestra la evolución de la burbuja, a medida que va perdiendo aire por el tubo. Se trata del mismo modelo estudiado en la página anterior, pero en sentido inverso

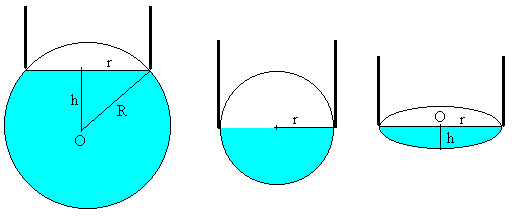
Cuando el radio de la burbuja r es mayor que el radio R del tubo

La burbuja tiene la forma de una esfera de radio R, cuyo centro está a una distancia h de la parte inferior del tubo.

${\displaystyle h=\sqrt{R^2-r^2}}$

Calculamos el volumen V de aire (en color azul).

${\displaystyle V=\pi \left(\frac{2}{3}{r}^3+r^2\sqrt{r^2-R^2}-\frac{1}{3}{\left(r^2-R^2\right)}^{3/2}\right)}$

Establecemos la relación entre el radio r de la burbuja y el tiempo t. Derivamos la expresión del volumen respecto de r, dV/dr, multiplicamos la expresión resultante por r e integramos entre el radio inicial r₀, en el instante t=0 y el radio r, en el instante t

${\displaystyle {\displaystyle \underset{r_0}{\overset{r}{\int }}\pi \left(2r^3+r^2\sqrt{r^2-R^2}+\frac{r^4}{\sqrt{r^2-R^2}}\right)}dr=-\frac{\pi \gamma R^4}{2\eta L}t}$

Esta integral se compone d ela suma de tres términos. La integral del primero es inmediata, la integral d elos otros dos términos requiere el cambio de variable r=Rcoshz. Los resultados parciales son los siguienets:

${\displaystyle \begin{array}{l}{\displaystyle \int r^2\sqrt{r^2-R^2}dr}=R^4{\displaystyle \int {\cosh }^{2}z{\sinh }^{2}z·dz=\frac{R^4}{8}}{\displaystyle \int \left(\cosh (4z)-1\right)dz}=\\ \frac{R^4}{8}\left(\frac{1}{4}\sinh (4z)-z\right)\\ {\displaystyle \int \frac{r^4}{\sqrt{r^2-R^2}}dr}=R^4{\displaystyle \int {\cosh }^{4}z·dz}=\frac{R^4}{8}{\displaystyle \int \left(\cosh (4z)+4\cosh (2z)+3\right)dz=}\\ \frac{R^4}{8}\left(\frac{1}{4}\sinh (4z)+2\sinh (2z)+3z\right)\end{array}}$

Sumando el segundo y tercer término del integrando

${\displaystyle R^4\left(\frac{1}{16}\sinh (4z)+\frac{1}{4}\sinh (2z)+\frac{1}{4}z\right)}$

Se deshacen los cambios utilizando las siguientes relaciones:

${\displaystyle \begin{array}{l}\sinh z=\frac{1}{2}\left(e^z-e^{-z}\right)\\ \cosh z=\frac{1}{2}\left(e^z+e^{-z}\right)\\ {\cosh }^{2}z-{\sinh }^{2}z=1\\ \sinh (2z)=2\sinh z·\cosh z\\ \cosh z=\frac{r}{R}z=\log \left(\frac{r}{R}+\sqrt{\frac{r^2}{R^2}-1}\right)\end{array}}$

El resultado final de la suma de los tres términos del integrando es

${\displaystyle {\frac{r^4}{2}+\frac{1}{2}{r}^3\sqrt{r^2-R^2}+\frac{1}{4}{R}^{2}r\sqrt{r^2-R^2}+\frac{1}{4}{R}^4\log \left(\frac{r}{R}+\sqrt{\frac{r^2}{R^2}-1}\right)|}_{r_0}^r=-\frac{\gamma R^4}{2\eta L}t}$

Dividiendo entre R⁴ y multiplicando por 2

${\displaystyle \begin{array}{l}f(x)-f(x_0)=-\frac{\gamma }{\eta L}t\\ f(x)=x^4+\frac{1}{2}\left(2x^2+1\right)x\sqrt{x^2-1}+\frac{1}{2}\log \left(x+\sqrt{x^2-1}\right)x=\frac{r}{R}\end{array}}$

Se trata de una ecuación implícita válida entre x=r₀/R y x=1

Cuando x=1, el radio de la burbuja se iguala al radio del tubo R empleando un tiempo t₀ en alcanzarlo

Cuando el radio de la burbuja r es menor que el radio R del tubo

La burbuja adopta la forma de un elipsoide de revolución. Una elipse de semieje mayor R y semieje menor h que gira alrededor del eje vertical Y

El volumen de la mitad del elipsoide (en color azul en la figura), es

${\displaystyle V=\frac{2}{3}\pi R^{2}h}$

El radio de curvatura de la elipse en la posición x=0 es r=R²/h.

Tenemos que relacionar h y el tiempo t

${\displaystyle \begin{array}{l}-\frac{dV}{dt}=\frac{\pi }{8}\frac{4\gamma }{r}\frac{R^4}{\eta L}\\ -\frac{d\left(\frac{2}{3}\pi R^{2}h\right)}{dt}=\frac{\pi }{8}\frac{4\gamma h}{R^2}\frac{R^4}{\eta L}\end{array}}$

Esta ecuación se integra de forma inmediata, sabiendo que en el instante t₀, h=R

${\displaystyle \begin{array}{l}{\displaystyle \underset{R}{\overset{h}{\int }}\frac{dh}{h}=}-\frac{3}{4}\frac{\gamma }{\eta L}{\displaystyle \underset{t_0}{\overset{t}{\int }}dt}\\ \frac{h}{R}=\exp \left(-\frac{3}{4}\frac{\gamma }{\eta L}(t-t_0)\right)\end{array}}$

Comparación del modelo y su aproximación

El tiempo que tarda la burbuja en alcanzar el radio R del tubo se calcula poniendo x=1 en las ecuaciones que describen cada una de las dos aproximaciones

${\displaystyle \begin{array}{l}f(x)-f(x_0)=-\frac{\gamma }{\eta L}t\\ x^4-x_0^4=-\frac{1}{2}\frac{\gamma }{\eta L}tx=\frac{r}{R}\end{array}}$

L=10;  %cm, longitud del tubo
R=0.1; %cm radio del tubo
r0=2.47;  %cm radio inicial de la pompa
eta=1.72e-5; %Ns/m^2, viscosidad del aire
gamma=0.022; %N/m, tensión superficial

%modelo 
k=gamma/(eta*L/100);
%primera etapa entre x0 y 1
x0=r0/R;
f=@(x) x.^4+(2*x.^2+1).*x.*sqrt(x.^2-1)/2+log(x+sqrt(x.^2-1))/2;
tf=(f(x0)-f(1))/k
%aproximación
tf=2*(x0^4-1)/k

t1 =   58.2001
t2 =   58.1999

Se obtiene el mismo tiempo

Calculamos el tiempo que la burbuja tarda en desaparecer r=0, o bien, x=0

${\displaystyle x_0^4=\frac{1}{2}\frac{\gamma }{\eta L}t}$

t2 =   58.2001

Un tiempo muy pequeño

En el modelo hemos supuesto que la burbuja toma la forma de un elipsoide de revolución de semiejes R el radio del tubo y h. La burbuja desaparece cuando h→0, se convierte en un disco plano de radio R. Tarda un tiempo infinito en desaparecer, aunque el valor elevado del exponente 3γ/(4ηL)=3200.7 hace que h→0 muy rápidamente

Representamos la evolución del radio r de la burbuja con el tiempo t, utilizando el modelo y la aproximación

L=10; %L=15.1; %cm, longitud del tubo
R=0.1;  %cm radio del tubo
r0=2.47; %cm radio inicial de la pompa
eta=1.72e-5;%eta=1.837e-5 %Ns/m^2, viscosidad del aire
gamma=0.022; %N/m, tensión superficial

%modelo de dos etapas
k=gamma/(eta*L/100);
%primera etapa entre x0 y 1
x0=r0/R;
f=@(x) x.^4+(2*x.^2+1).*x.*sqrt(x.^2-1)/2+log(x+sqrt(x.^2-1))/2;
x=linspace(x0,1,100);
t=(f(x0)-f(x))/k;
tf=(f(x0)-f(1))/k;
%segunda etapa entre 1 y 0
t2=linspace(tf,tf+0.5,10);
x1=exp(-3*k*(t2-tf)/4);
hold on
%aproximación
tf=2*(r0/R)^4/k;
y=@(t) ((r0/R)^4-k*t/2).^(1/4);
%gráficas
plot([t,t2],[x,x1])
fplot(y,[0,tf]);
line([0,t2(end)],[1,1],'LineStyle','--','Color','r')
hold off
grid on
legend('modelo','aproximación')
ylabel('r/R')
xlabel('t')
title('Burbuja que se desinfla')

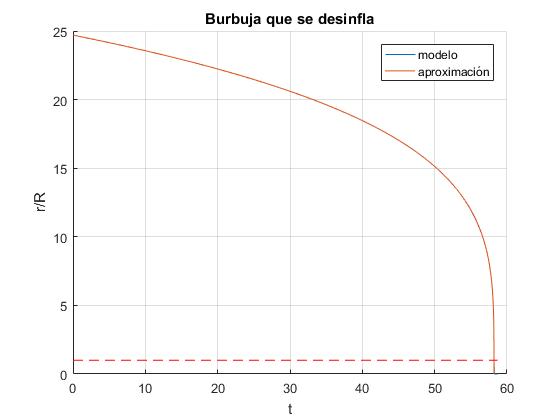
Vemos que el modelo de dos etapas explicado en esta sección coincide con la aproximación que hemos explicado en el primer apartado, el radio de la burbuja supuesta esférica disminuye con la raíz cuarta del tiempo

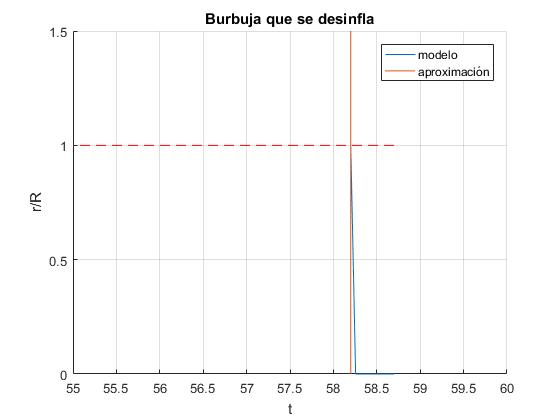
Las diferencias, aunque pequeñas, se manifiestan cuando el radio r de la burbuja es menor que el radio del tubo R. Añadimos las siguientes líneas de código al final del script, para apreciar esta pequeña diferencia

xlim([55,60])
ylim([0,1.5])

Actividades

1. Se introduce
• el radio R del capilar, en el control titulado Radio
• la longitud del capilar L, en el control titulado Longitud
2. Se pulsa el botón titulado Nuevo.
3. Se pulsa el botón titulado Inflar. El émbolo se desplaza en el interior de la jeringa, hasta su posición final, adquiriendo la burbuja un radio máximo r₀.
4. Se pulsa el botón titulado Desinflar. Se pone la burbuja en contacto con el tubo capilar. La burbuja se desinfla hasta que desaparece.
5. A partir de la medida del tiempo que tarda en desaparecer, se obtiene el valor de la tensión superficial de la solución jabonosa.

Referencias

Rämme G. Surface tension from deflating a soap bubble. Phys. Educ. 32 (3) May 1997. pp 191-194.

David P. Jackson, Sarah Sleyman. Analysis of a deflating soap bubble Am. J. Phys. 78 (10) October 2010