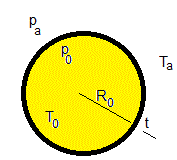
Supongamos una pompa jabón de forma esférica de radio R₀ y espesor t<<R₀, hecha de un jabón de tensión superficial γ y densidad ρ_s. El aire en su interior tiene densidad ρ₀, presión p₀, y temperatura T₀. El aire en el exterior tiene una presión p_a, densidad ρ_a y temperatura T_a.

Como se ha explicado en la página titulada 'Presión producida por la curvatura de una superficie', la diferencia entre las presión en el interior p₀ y exterior p_a de una pompa de jabón de radio R₀ es

${\displaystyle p_0-p_a=\frac{4\gamma }{R_0}}$

Escribimos la ecuación de los gases perfectos en términos de la presión p, densidad ρ y temperatura T del gas. M se denomina masa molar

${\displaystyle \begin{array}{l}pV=\frac{m}{M}RT\\ p=\frac{\rho }{M}RT\end{array}}$

Relacionamos las presiones, densidades y temperaturas del aire en el interior y en el exterior de la pompa de jabón

${\displaystyle \frac{{\rho }_0{T}_0}{{\rho }_a{T}_a}=\frac{p_0}{p_a}=1+\frac{4\gamma }{p_a{R}_0}}$

Con los datos de

• Tensión superficial del jabón, γ=0.025 N/m
• Radio de la pompa de jabón, R₀= 1.0 cm
• Presión atmosférica, p_a=1.013·10⁵ N/m²

${\displaystyle \frac{{\rho }_0{T}_0}{{\rho }_a{T}_a}=\frac{p_0}{p_a}=1+0.0000987}$

El efecto de la tensión superficial es muy pequeño

La pompa de jabón flota en el aire

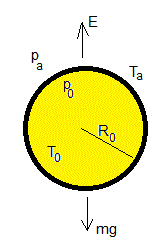
La pompa de jabón flota en el aire si la temperatura del aire en su interior T₀ es superior a un valor mínimo

Para que flote el peso mg de la pompa de jabón tiene que ser menor o igual al empuje E del aire.

La pompa de jabón se compone de una esfera hueca de radio R₀ y espesor t hecha de jabón de densidad ρ_s y el aire en su interior de densidad ρ₀. Si el espesor t de la esfera hueca es pequeño frente a radio R₀, el volumen de jabón es, aproximadamente

${\displaystyle \frac{4}{3}\pi {(R_0+t)}^3-\frac{4}{3}\pi R_0^3\approx 4\pi R_0^{2}t}$

El peso de la pompa es

${\displaystyle {\rho }_{s}g\left(4\pi R_0^{2}t\right)+{\rho }_{0}g\left(\frac{4}{3}\pi R_0^3\right)}$

El empuje que experimenta una esfera de radio R₀ en el aire exterior de densidad ρ_a es

${\displaystyle {\rho }_{a}g\left(\frac{4}{3}\pi R_0^3\right)}$

Para que la pompa flote en el aire se tiene que cumplir que

${\displaystyle \begin{array}{l}{\rho }_{a}g\left(\frac{4}{3}\pi R_0^3\right)\ge {\rho }_{s}g\left(4\pi R_0^{2}t\right)+{\rho }_{0}g\left(\frac{4}{3}\pi R_0^3\right)\\ \left({\rho }_a{R}_0-3{\rho }_{s}t\right)\ge \frac{{\rho }_a{T}_a}{T_0}{R}_0\left(1+\frac{4\gamma }{p_a{R}_0}\right)\\ T_0\ge \frac{{\rho }_a{R}_0}{{\rho }_a{R}_0-3{\rho }_{s}t}{T}_a\left(1+\frac{4\gamma }{p_a{R}_0}\right)\end{array}}$

Con los datos de

• Tensión superficial del jabón, γ=0.025 N/m
• Radio de la pompa de jabón, R₀= 1.0 cm
• Presión atmosférica, p_a=1.013·10⁵ N/m²
• Temperatura del aire exterior, T_a=300 K
• Densidad del aire exterior, ρ_a=1.30 kg/m³
• Densidad del jabón, ρ_s=1000 kg/m³
• Espesor de la pompa de jabón, t=100·10^-9 m

T₀>307.12 K. La temperatura del aire en el interior de la pompa de jabón tiene ser 7.12 °C más a caliente que la del aire que la rodea.

Movimiento de la pompa de jabón en el aire

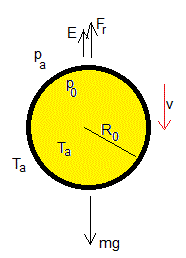
Supongamos que el aire en el interior y en el exterior de la pompa tienen la misma temperatura T_a, por que se ha establecido el equilibrio térmico.

Sobre la pompa de jabón actúan tres fuerzas: el peso, mg, el empuje E y la fuerza de rozamiento F_r. Suponiendo que el número de Reynolds es pequeño, la fórmula de Stokes para el movimiento del una esfera de radio R es F_r=6πRηv. Donde η es la viscosidad del fluido

${\displaystyle m\frac{dv}{dt}=(mg-E)-6\pi R_0\eta v}$

Se trata de una ecuación diferencial de variables separadas que se puede integrar fácilmente

${\displaystyle \begin{array}{l}\frac{dv}{dt}=a-bvv=\frac{a}{b}\left(1-\exp (-bt)\right)\\ b=\frac{9\eta }{2R_0\left(3{\rho }_{s}t+{\rho }_0{R}_0\right)}\\ a=g-\frac{E}{m}=g\left(1-\frac{{\rho }_a{R}_0}{3{\rho }_{s}t+{\rho }_0{R}_0}\right)\end{array}}$

En el primer apartado, relacionamos la densidad del aire en el interior de la pompa ρ₀, con la densidad en el exterior ρ_a y la temperaturas respectivas T₀ y T_a. Suponiendo que ambas temperaturas son iguales T₀=T_a

${\displaystyle {\rho }_0={\rho }_a\left(1+\frac{4\gamma }{p_a{R}_0}\right)}$

La contribución del término proporcional a la tensión superficial γ es pequeña frente a la unidad, por lo que ρ₀≈ρ_a

La velocidad límite constante vale

${\displaystyle v_{\infty }=\frac{a}{b}=\frac{2R_{0}g}{9\eta }\left(3{\rho }_{s}t+{\rho }_a\frac{4\gamma }{p_a}\right)}$

• La viscosidad del aire, η=1.8·10^-5 kg/(ms)

Con los datos proporcionados en el apartado anterior. La velocidad límite constante es v_∞=0.36 m/s. El parámetro b=0.609 s^-1 que aparece en la exponencial indica que la velocidad límite constante se alcanza en un tiempo pequeño 4 ó 5 segundos, aproximadamente

Como apreciamos de nuevo, el término prporcional a la tensión superficial γ es muy pequeño y por tanto, contribuye muy poco a la velocidad límite v_∞.

Se suministra una carga q a la pompa de jabón

La fuerza de repulsión entre las cargas eléctricas incrementa la presión del aire en el interior de la pompa de jabón. La presión electrostática es σ²/(2ε₀), donde σ es la densidad de carga en C/m²

La pompa de jabón incrementa su radio de R₀ a R₁, sin que haya cambio de temperatura (transformación isoterma)

${\displaystyle p_1\left(\frac{4}{3}\pi R_1^3\right)=p_0\left(\frac{4}{3}\pi R_0^3\right)}$

La diferencia de presión del aire en el interior p₁ y exterior p_a de la pompa de jabón vale

${\displaystyle p_1+\frac{{\sigma }^2}{2{\epsilon }_0}-p_a=\frac{4\gamma }{R_1}\sigma =\frac{q}{4\pi R_1^2}}$

Despejamos R₁/R₀

${\displaystyle {\left(\frac{R_1}{R_0}\right)}^4+\frac{4\gamma }{p_a{R}_0}{\left(\frac{R_1}{R_0}\right)}^3-\left(\frac{4\gamma }{p_a{R}_0}+1\right)\left(\frac{R_1}{R_0}\right)-\frac{q^2}{32{\pi }^2{\epsilon }_0{R}_0^4{p}_a}=0}$

• Carga eléctrica suministrada, q=256·10^-9 C

Con los datos de los apartados anteriores, calculamos los coeficientes del polinomio de cuarto grado en x=R₁/R₀

${\displaystyle x^4+9.872·{10}^{-5}·x^3-1.0001·x-0.0232=0}$

gamma=0.025; %tensión superficial
pA=1.013e5; %presión atmosférica
R0=0.01; %radio de la pompa
q=2.56e-7; %carga de la pompa

a=4*gamma/(pA*R0);
b=q^2*4*9e9/(32*pi*R0^4*pA);
roots([1,a,0,-(1+a),-b])

ans =
   1.0076 + 0.0000i
  -0.4923 + 0.8662i
  -0.4923 - 0.8662i
  -0.0232 + 0.0000i

La raíz real positiva es R₁/R₀=1.0076

Se desprecia la tensión superficial γ≈0

${\displaystyle {\left(\frac{R_1}{R_0}\right)}^4-\left(\frac{R_1}{R_0}\right)-\frac{q^2}{32{\pi }^2{\epsilon }_0{R}_0^4{p}_a}=0}$

Si R₁ y R₀ difieren en una pequeña cantidad por que la carga q es pequeña, R₁=R₀+ΔR

${\displaystyle \begin{array}{l}\frac{R_1}{R_0}=1+\frac{\Delta R}{R_0}\\ {\left(\frac{R_1}{R_0}\right)}^4=1+4\frac{\Delta R}{R_0}\end{array}}$

Despejamos ΔR

${\displaystyle \begin{array}{l}\Delta R\approx \frac{q^2}{96{\pi }^2{\epsilon }_0{R}_0^3{p}_a}\\ \frac{R_1}{R_0}=1+\frac{q^2}{96{\pi }^2{\epsilon }_0{R}_0^4{p}_a}\end{array}}$

Con los datos proporcionados, R₁=1.0019

La pompa de jabón cargada flota en el aire

Queremos calcular la carga mínima q necesaria para que la pompa de jabón flote.

Hemos calculado en el segundo apartado, el peso de una pompa de jabón de radio R₀

${\displaystyle {\rho }_{s}g\left(4\pi R_0^{2}t\right)+{\rho }_{0}g\left(\frac{4}{3}\pi R_0^3\right)}$

Donde ρ₀=ρ_a(1+4γ/(p_a·R₀)). La contribución del término proporcional a la tensión superficial γ es pequeña frente a la unidad, por lo que ρ₀≈ρ_a

Suministramos a la pompa de jabón una carga q, con lo que su radio aumenta a R₁. El peso no cambia y el empuje del aire es

${\displaystyle {\rho }_{a}g\left(\frac{4}{3}\pi R_1^3\right)}$

El empuje deberá se mayor que el peso

${\displaystyle \begin{array}{l}{\rho }_{a}g\left(\frac{4}{3}\pi R_1^3\right)\ge {\rho }_{s}g\left(4\pi R_0^{2}t\right)+{\rho }_{0}g\left(\frac{4}{3}\pi R_0^3\right)\\ {\rho }_a{R}_0^3{\left(1+\frac{\Delta R}{R_0}\right)}^3\ge 3{\rho }_s{R}_0^{2}t+{\rho }_a{R}_0^3\\ {\rho }_a\Delta R\ge {\rho }_{s}t\end{array}}$

Utilizamos la relación aproximada entre el incremento del radio ΔR y la carga q

${\displaystyle \frac{q^2}{96{\pi }^2{\epsilon }_0{R}_0^3{p}_a}\ge \frac{{\rho }_s}{{\rho }_a}t}$

Con los datos proporcionados, q≥2.56·10^-7 C

Referencias

Problema propuesto en la XLII Olimpiada Internacional de Física. Bangkok (2011)