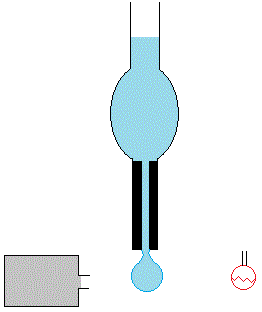
Para medir la tensión superficial se fotografían las gotas de líquido que cuelgan de un capilar conectado a un pequeño depósito de líquido, el estalagmómetro.

A la izquierda, se muestra la cámara fotográfica y a la derecha, la fuente de luz

Un programa de tratamiento de imágenes nos proporciona el perfil de la gota, a partir del cual se mide la tensión superficial del líquido. Véase el artículo mencionado en las referencias

El análisis del perfil de la gota se fundamenta en la ecuación de Young-Laplace que describe la diferencia de presión entre el interior y el exterior de la superficie curva de un líquido.

${\displaystyle \Delta p=p_{\text{int}}-p_{\text{ext}}=\gamma \left(\frac{1}{R_1}+\frac{1}{R_2}\right)}$

Donde R₁ y R₂ son los radios de curvatura de la superficie curva del líquido en el punto P

Radios de curvatura

La gota es una superficie de revolución que se obtiene haciendo girar la función z=f(x) alrededor del eje Z.

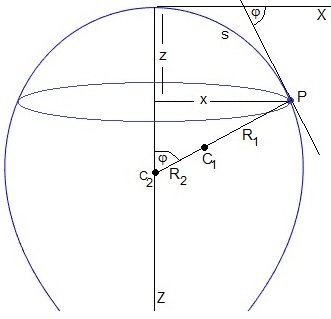
Trazamos un plano tangente a la superficie de la gota que pasa por el punto P. La recta perpendicular a dicho plano que pasa por P es la normal.

Se obtiene el perfil de la gota, cortando la gota por el plano y=0, el perfil de la gota viene descrito por la función z=f(x).

El radio de curvatura principal R₁ se obtiene igual que para cualquier otra función de una variable.

${\displaystyle R_1=\frac{{\left(1+{\left(\frac{dz}{dx}\right)}^2\right)}^{3/2}}{\frac{d^{2}z}{d{x}^2}}}$

Como se trata de una superficie de revolución, el centro de curvatura C₂ está en el eje y el radio de curvatura R₂, es

${\displaystyle R_2=\frac{x}{\sin \phi }}$

En la parte superior de la gota, x=0, z=0, los radios de curvatura son iguales R₁=R₂=R

La presión en P es la debida a la altura de fluido ρgz y a la presión debido a dicha curvatura

${\displaystyle \Delta p=\rho gz+\gamma \left(\frac{1}{R}+\frac{1}{R}\right)=\rho gz+\gamma \frac{2}{R}}$

La ecuación diferencial que describe el perfil de la gota suspendida

La ecuación de Young-Laplace se escribe

${\displaystyle \frac{1}{R_1}+\frac{\sin \phi }{x}=\frac{\rho gz}{\gamma }+\frac{2}{R}}$

Sustituyendo el radio de curvatura R₁ y teniendo en cuenta la relación trigonométrica,

${\displaystyle \sin \phi =\frac{\tan \phi }{\sqrt{1+{\tan }^2\phi }}=\frac{\frac{dz}{dx}}{\sqrt{1+{\left(\frac{dz}{dx}\right)}^2}}}$

Obtenemos la ecuacion diferencial

${\displaystyle \frac{\frac{d^{2}z}{d{x}^2}}{{\left(1+{\left(\frac{dz}{dx}\right)}^2\right)}^{3/2}}+\frac{1}{x}\frac{\frac{dz}{dx}}{\sqrt{1+{\left(\frac{dz}{dx}\right)}^2}}=\frac{\rho gz}{\gamma }+\frac{2}{R}}$

La escribimos en términos de variables adimensionales, X=x/R, Z=z/R

${\displaystyle \begin{array}{l}\frac{\frac{d^{2}Z}{d{X}^2}}{{\left(1+{\left(\frac{dZ}{dX}\right)}^2\right)}^{3/2}}+\frac{1}{X}\frac{\frac{dZ}{dX}}{\sqrt{1+{\left(\frac{dZ}{dX}\right)}^2}}=\frac{\rho g{R}^2}{\gamma }Z+2\\ \frac{d^{2}Z}{d{X}^2}+\left(1+{\left(\frac{dZ}{dX}\right)}^2\right)\frac{1}{X}\frac{dZ}{dX}=\left(\beta Z+2\right){\left(1+{\left(\frac{dZ}{dX}\right)}^2\right)}^{3/2}\end{array}}$

Esta ecuación no es adecuada para resolverla numéricamente con las condiciones iniciales, X=0, Z=0, dZ/dX=0. Vamos a sustituir esta ecuación diferencial por un sistema de tres ecuaciones diferenciales

Sistema de tres ecuaciones diferenciales

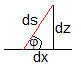
Sea s la longitud del arco del punto P medido desde el origen. La longitud ds de un elemento diferencial del perfil de la curva alrededor de P es

${\displaystyle \begin{array}{l}dx=ds\cos \phi ,dz=ds\sin \phi \\ ds=R_{1}d\phi \end{array}}$

La ecuación de Young-Laplace se escribe

${\displaystyle \frac{d\phi }{ds}+\frac{\sin \phi }{x}=\frac{\rho gz}{\gamma }+\frac{2}{R}}$

Resolveremos el sistema de tres ecuaciones diferenciales

${\displaystyle \{\begin{array}{l}\frac{d\phi }{ds}+\frac{\sin \phi }{x}=\frac{\rho gz}{\gamma }+\frac{2}{R}\\ \frac{dz}{ds}=\sin \phi \\ \frac{dx}{ds}=\cos \phi \end{array}}$

Es conveniente expresarlas en términos de variables adimensionales, X=x/R, Z=z/R, S=s/R

${\displaystyle \{\begin{array}{l}\frac{d\phi }{dS}+\frac{\sin \phi }{X}=\beta Z+2\\ \frac{dZ}{dS}=\sin \phi \\ \frac{dX}{dS}=\cos \phi \end{array}}$

En el artículo citado en las referencias, se emplea este sistema de tres ecuaciones diferenciales para representar el perfil de una gota suspendida en términos del parámetro β

Se resuelve numéricamente este sistema, mediante el procedimiento ode45 de MATLAB, con las siguientes condiciones iniciales φ=0, X≈0, Z≈0

beta=0.24;
%phi=x(1), x=x(2), z=x(3), s=t
f=@(t,x) [2-beta*x(3)-sin(x(1))/x(2); cos(x(1)); sin(x(1))]; 
[t,x]=ode45(f,[0,3],[0, 1e-23, 1e-23]);
phi=linspace(0,2*pi,length(x(:,2)));
X=x(:,2).*cos(phi);
Y=x(:,2).*sin(phi);
Z=repmat(x(:,3),1,length(x(:,3)));
surfl(X,Y,Z)
shading interp
colormap(gray);
axis equal
xlabel('x'); ylabel('y'); zlabel('z')
title('Gota de agua suspendida')
view(-33,16)

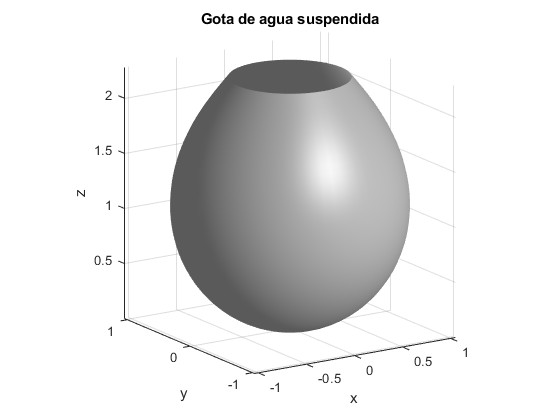
Representamos el perfil de la gota, la función Z=f(X), para tres valores del parámetro β, 0.15, 0.24 y 0.45

%phi=x(1), x=x(2), z=x(3), s=t
hold on
for beta=[0.15,0.24,0.45]
    f=@(t,x) [2-beta*x(3)-sin(x(1))/x(2); cos(x(1)); sin(x(1))]; 
    [t,x]=ode45(f,[0,3],[0, 1e-23, 1e-23]);
    plot(x(:,2),x(:,3),'displayName',num2str(beta))
end
hold off
grid on
axis equal
xlabel('X')
legend('-DynamicLegend','location','best')
ylabel('Z')
title('Gota de agua suspendida')

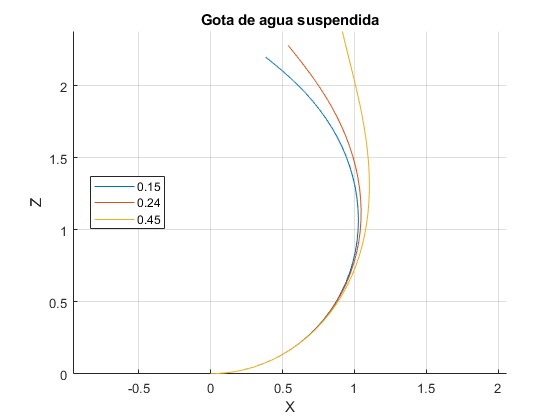
El perfil de la gota es simétrico respecto del eje Z, por lo que solamente representamos la solución del sistema de tres ecuaciones diferenciales para X≥0

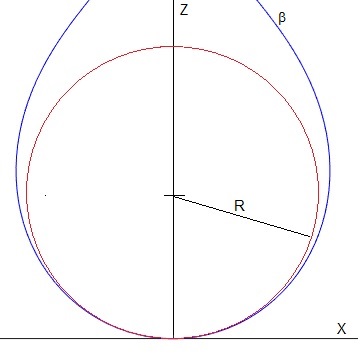
El procedimiento de medida de la tensión superficial γ es el siguiente:

• Determinamos el valor del parámetro β que mejor ajusta al perfil de la gota real

• Medimos el radio de curvatura R del la gota en el origen x=0, z=0

• Calculamos la tensión superficial γ, mediante la fórmula

${\displaystyle \gamma =\frac{\rho g{R}^2}{\beta }}$

ρ es la densidad del fluido y g=9.8 m/s² es la aceleración de la gravedad

Referencias

Ehsan Yakhshi-Tafti, Ranganathan Kumar, Hyoung J. Cho. Measurement of Surface Interfacial Tension as a Function of Temperature Using Pendant Drop Images. International Journal of Optomechatronics. 14 Dec 2011.