Forma de la superficie de un líquido en contacto con una placa vertical

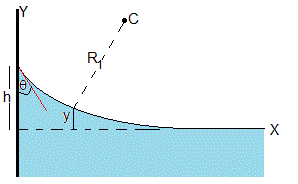
Supongamos que una placa muy larga se introduce en un líquido. La superficie del líquido cerca de la placa deja de ser plana. Vamos a obtener la ecuación del perfil de dicha superficie en términos de la densidad del líquido ρ, coeficiente de tensión superficial γ, y el ángulo de contacto θ

Cortamos la superficie del líquido por un plano vertical perpendicular a la placa. Establecemos los ejes X e Y. El perfil de dicha superficie es la función y=y(x) que vamos a determinar

Aplicamos la ecuación Young-Laplace para la superficie curva de un líquido

${\displaystyle \Delta p=\gamma \left(\frac{1}{R_1}+\frac{1}{R_2}\right)=\frac{\gamma }{R_1}}$

Uno de los radios de curvatura es infinito, 1/R₂=0. Se traza la tangente a la curva en el punto (x,y). En la perpendicular (normal) se encuentra el centro de curvatura C, cuyo radio es R₁

La presión es mayor del lado del centro de curvatura, la diferencia Δp es la altura y de la columna de fluido

${\displaystyle \rho gy=\gamma \frac{\frac{d^{2}y}{d{x}^2}}{{\left(1+{\left(\frac{dy}{dx}\right)}^2\right)}^{3/2}}}$

Para una función decreciente d²y/dx²>0

Multiplicamos el miembro izquierdo por dy y el miembro derecho, por su equivalente, (dy/dx)dx e integramos

${\displaystyle \frac{\rho g}{\gamma }{\displaystyle \int y·dy=}{\displaystyle \int \frac{\frac{d^{2}y}{d{x}^2}\frac{dy}{dx}}{{\left(1+{\left(\frac{dy}{dx}\right)}^2\right)}^{3/2}}dx}}$

La primera integral es inmediata, para la segunda hacemos el cambio de variable

${\displaystyle {\displaystyle \int \frac{u}{{\left(1+u^2\right)}^{3/2}}}·du=-\frac{1}{\sqrt{1+u^2}},u(x)=\frac{dy}{dx},du=\frac{d^{2}y}{d{x}^2}dx}$

El resultado es

${\displaystyle \frac{1}{2}\frac{\rho g}{\gamma }{y}^2=-\frac{1}{\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}}+c_1}$

La constante c₁ se determina, con la condición x→∞, y=0, dy/dx=0. Por tanto, c₁=1

${\displaystyle \frac{1}{2}\frac{\rho g}{\gamma }{y}^2=1-\frac{1}{\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}}}$

Para x=0 obtenemos la altura máxima del líquido h, donde la pendiente es -(π/2-θ)=-π/2+θ. Siendo θ el ángulo de contacto

${\displaystyle \frac{dy}{dx}=-\frac{1}{\tan \theta }}$

La altura h vale

${\displaystyle \begin{array}{l}\frac{1}{2}\frac{\rho g}{\gamma }{h}^2=1-\frac{1}{\sqrt{1+\frac{1}{{\tan }^2\theta }}}\\ \frac{1}{2}\frac{\rho g}{\gamma }{h}^2=1-\sin \theta \\ h^2=2\frac{\gamma }{\rho g}\left(1-\sin \theta \right)\end{array}}$

Integramos de nuevo, para obtener la ecuación del perfil de la superficie del líquido y=y(x)

${\displaystyle \begin{array}{l}\frac{1}{\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}}=1-\frac{k^2}{2}{y}^2,k^2=\frac{\rho g}{\gamma }\\ \frac{1}{1+{\left(\frac{dy}{dx}\right)}^2}={\left(1-\frac{k^2}{2}{y}^2\right)}^2\\ \frac{dy}{dx}=-k\frac{y\sqrt{1-\frac{k^2}{4}{y}^2}}{1-\frac{k^2}{2}{y}^2}\end{array}}$

Se elige el signo negativo de la raíz, por que la pendiente dy/dx es negativa. Integramos

${\displaystyle {\displaystyle \int \frac{1-\frac{k^2}{2}{y}^2}{y\sqrt{1-\frac{k^2}{4}{y}^2}}dy=-}k{\displaystyle \int dx}+c_2}$

La primera integral es la suma de dos

${\displaystyle {\displaystyle \int \frac{1-\frac{k^2}{2}{y}^2}{y\sqrt{1-\frac{k^2}{4}{y}^2}}dy=}{\displaystyle \int \frac{1}{y\sqrt{1-\frac{k^2}{4}{y}^2}}dy-}{\displaystyle \int \frac{\frac{k^2}{2}y}{\sqrt{1-\frac{k^2}{4}{y}^2}}dy}}$

Para la segunda integral, más sencilla, hacemos el cambio de variable

${\displaystyle u=1-\frac{k^2}{4}{y}^2,du=-\frac{k^2}{2}y·dy}$

Para la primera, hacemos el cambio de variable

${\displaystyle u^2=1-\frac{k^2}{4}{y}^2,y=\frac{2}{k}\sqrt{1-u^2},dy=-\frac{2}{k}\frac{u·du}{\sqrt{1-u^2}}}$

El resultado de la integral es

${\displaystyle {\displaystyle \int \frac{1-\frac{k^2}{2}{y}^2}{y\sqrt{1-\frac{k^2}{4}{y}^2}}dy=}-\text{arctanh}\left(\sqrt{1-\frac{k^2}{4}{y}^2}\right)+\sqrt{4-k^2{y}^2}}$

>> syms x k;
>> int((1-k*x^2/2)/(x*sqrt(1-k*x^2/4)),x)
ans =2*(1 - (k*x^2)/4)^(1/2) - atanh((1 - (k*x^2)/4)^(1/2))

Simplificamos algo más el resultado

${\displaystyle \begin{array}{l}t=\text{arctanh}\sqrt{1-\frac{k^2}{4}{y}^2}\\ \tanh t=\sqrt{1-\frac{k^2}{4}{y}^2}\\ \frac{k^2}{4}{y}^2=1-{\tanh }^{2}t\\ \frac{k}{2}y=\frac{1}{\cosh t}\\ t=\text{arccosh}\left(\frac{2}{ky}\right)\end{array}}$

El resultado es

${\displaystyle \sqrt{4-k^2{y}^2}-\text{arccosh}\left(\frac{2}{ky}\right)=-kx+c_2}$

La constante c₂ se calcula, con la condición, para x=0, y=h

${\displaystyle c_2=\sqrt{4-k{h}^2}-\text{arccosh}\left(\frac{2}{h\sqrt{k}}\right)}$

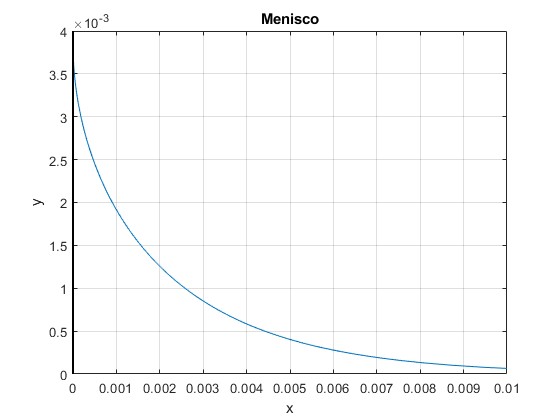
Llegamos a la ecuación implícita x=x(y) que describe el perfil de la superficie del líquido en contacto con una placa plana vertical

${\displaystyle \begin{array}{l}kx=\text{arccosh}\left(\frac{2}{ky}\right)-\sqrt{4-k^2{y}^2}-\text{arccosh}\left(\frac{2}{kh}\right)+\sqrt{4-k^2{h}^2},k^2=\frac{\rho g}{\gamma }\\ h^2=\frac{2}{k^2}\left(1-\sin \theta \right)\end{array}}$

Ejemplo

Para el agua en contacto con una placa plana metálica

• Angulo de contacto, θ≈0
• Densidad, ρ=1000 kg/m³
• Coeficiente de tensión superficial, γ=72.8·10^-3 N/m

k=sqrt(1000*9.8/72.8e-3);
h=sqrt(2)/k;
f=@(x,y) -sqrt(4-(k*y).^2)+acosh(2./(k*y))+sqrt(4-(k*h)^2)-acosh(2./(k*h))-x*k;
fimplicit(f,[0,0.01,0,h])
line([0,0],[0,4e-3],'lineWidth',1.5,'color','k')
grid on
xlabel('x')
ylabel('y')
title('Menisco')

Puente líquido entre dos placas planas paralelas

Dos placas planas se puede atraer con gran fuerza si el líquido entre ellas tiene un ángulo de contacto θ<π/2

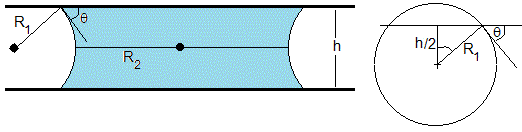
Un volumen V de líquido se sitúa entre dos placas planas paralelas separadas una distancia h. La ecuación de Young-Laplace se expresa de forma simple en el plano de simetría del puente líquido, donde los radios de curvatura son R₁ y R₂ y los centros de curvatura está señalados por pequeños círculos de color negro.

${\displaystyle \Delta p=\gamma \left(\frac{1}{R_1}-\frac{1}{R_2}\right)}$

Aproximamos la forma del menisco a un arco de circunferencia de radio R₁. El radio R₁ está relacionado con la separación entre las placas h y el ángulo de contacto θ

${\displaystyle R_1=\frac{h}{2\cos \theta }}$

Como R₁<R₂, la presión es menor en el interior del líquido y la fuerza que origina esta diferencia de presión es atractiva entre las placas.

Si h<<R₂, el volumen de líquido es $V\approx \pi R_2^{2}h$, la diferencia de presión y la fuerza de atracción son, aproximadamente,

${\displaystyle \begin{array}{l}\Delta p\approx \frac{2\gamma \cos \theta }{h}\\ F=\pi R_2^2\Delta p\end{array}}$

Ejemplo

Para R₂=1 cm y h=5μm. Suponiendo un ángulo de contacto θ≈0, si el líquido es agua, cuyo coeficiente de tensión superficial es γ=72.8·10^-3 N/m

Δp=29120 N/m²=0.29 atm

La fuerza de atracción entre las placas, F=9.1 N

Conocido el volumen del puente líquido

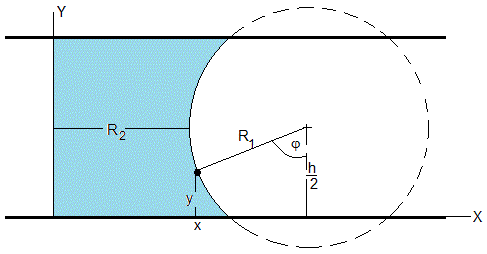
Conocido el volumen V de líquido determinamos el radio R₂

Las coordenadas de un punto del menisco son

${\displaystyle \{\begin{array}{l}x=R_1+R_2-R_1\sin \phi \\ y=\frac{h}{2}-R_1\cos \phi \end{array}}$

Eliminamos el ángulo φ, expresando x en función de la altura y comprendida entre 0 y h

${\displaystyle x=R_1+R_2-\sqrt{R_1^2-{\left(\frac{h}{2}-y\right)}^2}}$

El volumen de líquido es

${\displaystyle \begin{array}{l}V={\displaystyle \underset{0}{\overset{h}{\int }}(\pi x^2})dy\\ V=\pi {\displaystyle \underset{0}{\overset{h}{\int }}{\left(R_1+R_2-\sqrt{R_1^2-{\left(\frac{h}{2}-y\right)}^2}\right)}^2}dy\\ V=\pi {\displaystyle \underset{0}{\overset{h}{\int }}\left({\left(R_1+R_2\right)}^2+R_1^2-{\left(\frac{h}{2}-y\right)}^2-2\left(R_1+R_2\right)\sqrt{R_1^2-{\left(\frac{h}{2}-y\right)}^2}\right)}dy\\ V=\pi {\displaystyle \underset{0}{\overset{h}{\int }}\left(\left({\left(R_1+R_2\right)}^2+R_1^2-\frac{h^2}{4}\right)-y^2+hy-2\left(R_1+R_2\right)R_1\sqrt{1-{\left(\frac{\frac{h}{2}-y}{R_1}\right)}^2}\right)}dy\end{array}}$

Las primeras son integrales inmediatas, resolvemos la integral, haciendo el cambio de variable, h/2-y=R₁sint, dy=-R₁cost·dt

${\displaystyle \begin{array}{l}{\displaystyle \int \sqrt{1-{\left(\frac{\frac{h}{2}-y}{R_1}\right)}^2}·dy}=-R_1{\displaystyle \int {\cos }^{2}t·dt}=-\frac{R_1}{2}{\displaystyle \int \left(1+\cos (2t)\right)·dt}=-\frac{R_1}{2}\left(t+\frac{1}{2}\sin \left(2t\right)\right)=\\ -\frac{R_1}{2}\left(\arcsin \left(\frac{\frac{h}{2}-y}{R_1}\right)+\left(\frac{\frac{h}{2}-y}{R_1}\right)\sqrt{1-{\left(\frac{\frac{h}{2}-y}{R_1}\right)}^2}\right)\end{array}}$

Evaluamos el integrando entre los límites 0 y h

${\displaystyle \begin{array}{l}V=\pi {\left\{\left({\left(R_1+R_2\right)}^2+R_1^2-\frac{h^2}{4}\right)y-\frac{y^3}{3}+h\frac{y^2}{2}+\left(R_1+R_2\right)R_1^2\left(\arcsin \left(\frac{\frac{h}{2}-y}{R_1}\right)+\left(\frac{\frac{h}{2}-y}{R_1}\right)\sqrt{1-{\left(\frac{\frac{h}{2}-y}{R_1}\right)}^2}\right)\right\}}_0^h=\\ \pi \left\{\left({\left(R_1+R_2\right)}^2+R_1^2\right)h-\frac{h^3}{12}+\left(R_1+R_2\right)R_1^2\left(\arcsin \left(-\frac{h}{2R_1}\right)-\left(\frac{h}{2R_1}\right)\sqrt{1-{\left(\frac{-h}{2R_1}\right)}^2}\right)-\left(R_1+R_2\right)R_1^2\left(\arcsin \left(\frac{h}{2R_1}\right)+\left(\frac{h}{2R_1}\right)\sqrt{1-{\left(\frac{h}{2R_1}\right)}^2}\right)\right\}\end{array}}$

Simplificando la expresión, el volumen es

${\displaystyle \begin{array}{l}V=\pi \left\{\left({\left(R_1+R_2\right)}^2+R_1^2\right)h-\frac{h^3}{12}-\left(R_1+R_2\right)R_1^2\left(2\arcsin \left(\frac{h}{2R_1}\right)+\frac{h}{R_1}\sqrt{1-{\left(\frac{h}{2R_1}\right)}^2}\right)\right\}\\ R_1=\frac{h}{2\cos \theta }\end{array}}$

Con los datos del ejemplo anterior, calculmos los volúmenes

h=5e-6;
R2=0.01;
V=pi*R2^2*h; %aproximado
th=0;
R1=h/(2*cos(th));
V1=pi*(((R1+R2)^2+R1^2)*h-h^3/12-(R1+R2)*R1^2*(2*asin(h/(2*R1))+
h*sqrt(1-(h/(2*R1))^2)/R1)); %exacto
disp([V,V1])

   1.0e-08 *
    0.1571    0.1571

Obtenemos el mismo volumen

Conocidos el volumen, V, la separación entre las placas, h y el ángulo de contacto, θ, obtenemos una ecuación de segundo grado en R₂

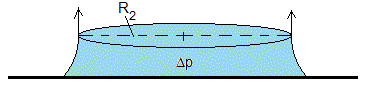
La fuerza en el plano de simetría del puente líquido

${\displaystyle F=2\pi R_2\gamma +\pi R_2^2\Delta p=2\pi R_2\gamma +\pi R_2^2\gamma \left(\frac{1}{R_1}-\frac{1}{R_2}\right)}$

El primer sumando es más pequeño que el segundo. La diferencia de presión y la tensión superficial contribuyen a mantener 'pegadas' las placas planas

Referencias

G. K. Batchelor. An Introduction to fluid dynamics. Cambridge University Press, pp. 66-67

James Bowen, David Cheneler. Closed-Form Expressions for Contact Angle Hysteresis: Capillary Bridges between Parallel Platens. Colloids and interfaces 2020 4, 13