La diferencia de presión Δp entre el interior y exterior de una burbuja esférica de radio r viene dada por la ecuación de Laplace

${\displaystyle \Delta p=\frac{4\gamma }{r}}$

El dispositivo experimental consiste en una jeringa conectada a un manómetro y a un tubo cilíndrico, de diámetro interior y exterior conocidos.

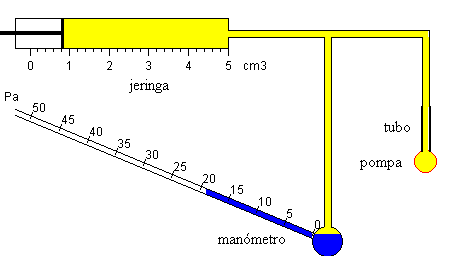
El manómetro consiste en un tubo inclinado conectado a un depósito de aceite de densidad conocida. El manómetro está graduado en Pa.

Se introduce y se saca el extremo libre de un tubo de diámetro conocido en una solución jabonosa. Se observa una lámina de fluido que se va convirtiendo en una burbuja a medida que se suministra aire con la jeringa. A su vez observamos en el manómetro que la presión crece hasta que se alcanza un máximo, cuando la burbuja tiene forma semiesférica con un radio igual al del tubo.

Una vez que se alcanza la máxima presión, si se continúa introduciendo aire actuando en la jeringa, el radio de la burbuja se incrementa mientras que la diferencia de presión entre el interior y el exterior de la burbuja disminuye de acuerdo a la ley de Laplace.

Cuando se ha introducido todo el aire de la jeringa, la burbuja tiene un radio r dado por

${\displaystyle V=\frac{4}{3}\pi r^3}$

donde V es el volumen de aire en la jeringa, que en nuestro caso es de 5 cm³

Modelo de evolución de la burbuja

En al figura, se muestra el modelo de la evolución de la burbuja, a medida que insuflamos un volumen de aire V con la jeringa, tal como ha sido simulada en el programa interactivo.

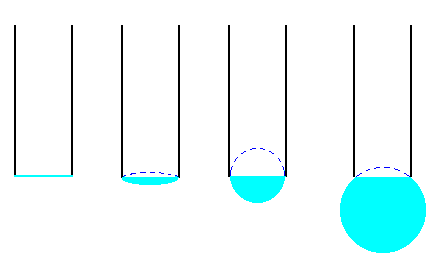
Vamos a calcular los volúmenes de aire (en color azul en las figuras) en los tres casos:

• r=R, el radio de la burbuja r es igual al radio del tubo R

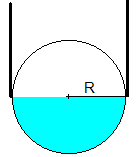
La situación límite se produce cuando el volumen de aire V (señalado en color azul en la figura), es igual al volumen de una semiesfera de radio R, el radio del tubo.

${\displaystyle V=\frac{2}{3}\pi R^3}$

 

• Cuando el volumen V de aire insuflado por la jeringa es mayor que 2πR³/3



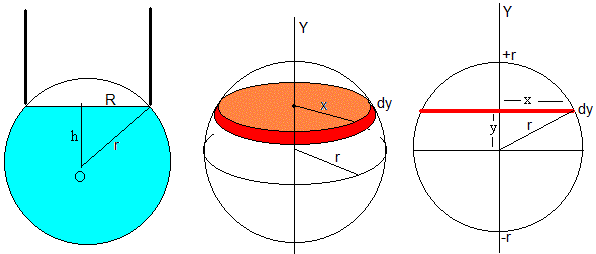
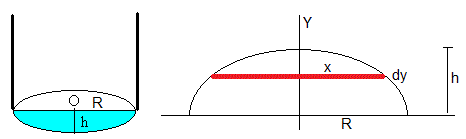
La burbuja tiene la forma de una esfera de radio R, cuyo centro está a una distancia h de la parte inferior del tubo.

${\displaystyle h=\sqrt{R^2-r^2}}$

Calculamos el volumen V de aire insuflado (en color azul) que es el volumen de la esfera de radio r, menos el volumen del casquete esférico que está en el interior del tubo.

El volumen del elemento diferencial señalado en color rojo en la figura central es un cilindro de radio x y de altura dy. Se suma todos los volúmenes comprendidos entre y=-r y y=h

${\displaystyle \begin{array}{l}V={\displaystyle \underset{-r}{\overset{h}{\int }}\pi x^{2}dy=}{\displaystyle \underset{-r}{\overset{h}{\int }}\pi \left(r^2-y^2\right)dy=}\pi \left(\frac{2}{3}{r}^3+r^{2}h-\frac{1}{3}{h}^3\right)=\\ \pi \left(\frac{2}{3}{r}^3+r^2\sqrt{r^2-R^2}-\frac{1}{3}{\left(r^2-R^2\right)}^{3/2}\right)\end{array}}$

Dado V y R, calculamos el radio de la burbuja x=r/R, mediante procedimientos numéricos

${\displaystyle \frac{V}{\frac{2}{3}\pi R^3}=\left(x^3+\frac{3}{2}{x}^2\sqrt{x^2-1}-\frac{1}{2}{\left(x^2-1\right)}^{3/2}\right)x=\frac{r}{R}}$

R=0.180; %cm radio del tubo
V=3.42; %cm3 volumen de aire
f=@(x) x.^3+3*(x.^2).*sqrt(x.^2-1)/2-(x.^2-1).^(3/2)/2-V/(2*pi*R^3/3);
r=fzero(f,[1,6])*R %radio de la burbuja

r =    0.9347

• Cuando el volumen V de aire insuflado por la jeringa es menor que 2πR³/3

La burbuja adopta la forma de un elipsoide de revolución. Una elipse de semieje mayor R y semieje menor h que gira alrededor del eje vertical Y

${\displaystyle \frac{x^2}{R^2}+\frac{y^2}{h^2}=1}$



El volumen de la mitad del elipsoide (en color azul en la figura), se calcula como la esfera, es

${\displaystyle V={\displaystyle \underset{0}{\overset{h}{\int }}\pi x^{2}dy=}{\displaystyle \underset{0}{\overset{h}{\int }}\pi R^2\left(1-\frac{y^2}{h^2}\right)dy=}\frac{2}{3}\pi R^{2}h}$

Calculamos el radio de curvatura de la elipse en la posición x=0. La fórmula que nos proporciona el radio de curvatura de una curva y=f(x) es

${\displaystyle r=\left|\frac{{\left(1+{\left(\frac{dy}{dx}\right)}^2\right)}^{3/2}}{\frac{d^{2}y}{d{x}^2}}\right|}$

Para una elipse

${\displaystyle \begin{array}{l}y=\frac{h}{R}\sqrt{R^2-x^2}\\ \frac{dy}{dx}=-\frac{h}{R}\frac{x}{\sqrt{R^2-x^2}}\\ \frac{d^{2}y}{d{x}^2}=-\frac{hR}{{\left(R^2-x^2\right)}^{3/2}}\end{array}}$

El radio de curvatura de la elipse en x=0 es r=R²/h. Cuando h→0, (tenemos una lámina circular en el extremo del tubo), el radio tiende a infinito r→∞.

Diferencia de presión

Una vez que disponemos del radio r de la burbuja calculamos la diferencia de presión del aire en el interior y exterior de la burbuja que marca el manómetro mediante la fórmula de Laplace.

${\displaystyle \Delta p=\frac{4\gamma }{r}}$

Cuando el volumen V de aire insuflado es cero, h=0 (r→∞) por tanto, no hay diferencia de presión Δp=0

R=0.405; %cm radio del tubo
gamma=0.025; %tensión superficial
V0=2*pi*R^3/3;
k=1;
V_=linspace(0,5,200);%cm3 volumen de aire
r=zeros(0,length(V_));
for V=V_
    if V<V0
        h=3*V/(2*pi*R^2); %semieje elipse
        r(k)=R^2/h;
    elseif V==V0
        r(k)=R; %radio del tubo
    else
        f=@(x) x.^3+3*(x.^2).*sqrt(x.^2-1)/2-(x.^2-1).^(3/2)/2-V/(2*pi*R^3/3);
        r(k)=fzero(f,[1,6])*R; %radio de la burbuja
    end
    k=k+1;
end
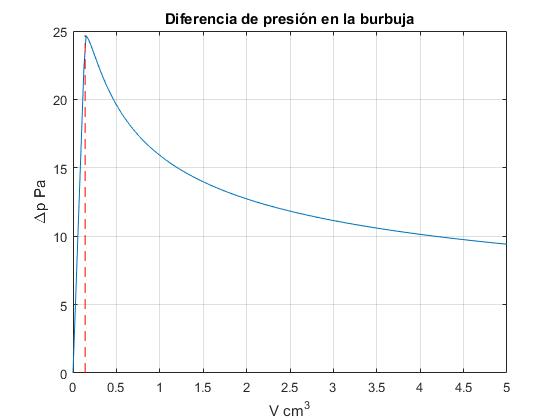
plot(V_,400*gamma./r)
line([V0,V0],[0,400*gamma./R], 'LineStyle','--','Color','r')
grid on
xlabel('V cm^3')
ylabel('\Deltap Pa')
title('Diferencia de presión en la burbuja')

Actividades

La tensión superficial se ha fijado en γ=0.025 N/m

• Se elige el radio r del tubo entre los siguientes (0.180, 0.220, 0.245, 0.300 y 0.405 cm) en el control titulado Radio del tubo:

Se pulsa el botón titulado Nuevo

• Se actúa sobre la barra de desplazamiento titulada Posición del émbolo para incrementar el radio de la burbuja

Observamos como cambia la diferencia de Δp presión en el manómetro.

Obtenemos el valor de la tensión superficial γ, cuando esta diferencia de presión se hace máxima entonces el radio de la burbuja r es igual al radio del tubo R.

${\displaystyle \gamma =\frac{\Delta p_{máx}·R}{4}}$

Alternativamente, obtenemos el valor de la tensión superficial γ cuando se ha insuflado todo el aire contenido en la jeringa V=5 cm³, el radio r de la burbuja es

${\displaystyle V=\frac{4}{3}\pi r^3\gamma =\frac{\Delta p·r}{4}}$

Al efectuar este cálculo, hemos despreciado el casquete esférico que está en el interior del tubo.

Referencias

Román F.L., Faro J., Velasco S. A simple experiment for measuring the surface tension of soap solutions. Am. J. Phys. 69 (8) August 2001 pp. 920-921.