El comando int(f,x,a,b) calcula la integral de la expresión f, respecto de la variable x, en el intervalo [a,b] donde a y b pueden ser cantidades numéricas o variables simbólicas.

Integrales indefinidas

Integrales inmediatas

${\displaystyle \begin{array}{l}\begin{array}{l}{{\displaystyle \int }}^{\text{}}{x}^{n}dx=\frac{x^{n+1}}{n+1}+C\hfill \\ {{\displaystyle \int }}^{\text{}}\frac{dx}{x}=\ln \left|x\right|+C\hfill \\ {{\displaystyle \int }}^{\text{}}{a}^{x}dx=\frac{a^x}{\ln a}+Ca>0{{\displaystyle \int }}^{\text{}}{e}^{x}dx=e^x+C\hfill \\ {{\displaystyle \int }}^{\text{}}\sin x·dx=-\cos x+C\hfill \\ {{\displaystyle \int }}^{\text{}}\cos x·dx=\sin x+C\hfill \\ {{\displaystyle \int }}^{\text{}}\frac{dx}{{\cos }^{2}x}=\tan x+C\hfill \\ {{\displaystyle \int }}^{\text{}}\frac{dx}{{\sin }^{2}x}=-\frac{1}{\tan x}+C\hfill \\ {{\displaystyle \int }}^{\text{}}\sinh x·dx=\cosh x+C\hfill \\ {{\displaystyle \int }}^{\text{}}\cosh x·dx=\sinh x+C\hfill \\ {{\displaystyle \int }}^{\text{}}\frac{dx}{{\cosh }^{2}x}=\tanh x+C\hfill \\ {{\displaystyle \int }}^{\text{}}\frac{dx}{{\sinh }^{2}x}=-\frac{1}{\tanh x}+C\hfill \\ {{\displaystyle \int }}^{\text{}}\frac{dx}{\sqrt{a^2-x^2}}=\arcsin \left(\frac{x}{a}\right)+C=-\arccos \left(\frac{x}{a}\right)+Ca>0\hfill \\ {{\displaystyle \int }}^{\text{}}\frac{dx}{x^2+a^2}=\frac{1}{a}\arctan \left(\frac{x}{a}\right)+C\hfill \end{array}\\ {{\displaystyle \int }}^{\text{}}\frac{dx}{\sqrt{x^2-a^2}}=\text{arccosh}\left(\frac{x}{a}\right)+C=\ln \left(x+\sqrt{x^2-a^2}\right)+C\\ {{\displaystyle \int }}^{\text{}}\frac{dx}{\sqrt{x^2+a^2}}=\text{arcsinh}\left(\frac{x}{a}\right)+C=\ln \left(x+\sqrt{x^2+a^2}\right)+C\\ {{\displaystyle \int }}^{\text{}}\frac{dx}{x^2-a^2}=-\frac{1}{a}\text{arctanh}\left(\frac{x}{a}\right)+C=-\frac{1}{a}\ln \sqrt{\frac{a+x}{a-x}}\end{array}}$

Si no ponemos límites a la integral, obtenemos la integral indefinida, la función cuya derivada es el integrando

${\displaystyle {\displaystyle \int {\sin }^2(x)·dx={\displaystyle \int \frac{1-\cos (2x)}{2}dx=}}\frac{1}{2}x-\frac{\sin (2x)}{4}+C}$

>> syms x;
>> z=int(sin(x)^2)
z =x/2 - sin(2*x)/4
>> y=diff(z)
y =1/2 - cos(2*x)/2
>> simplify(y)
ans =sin(x)^2

Calculamos la derivada con diff, simplificamos la expresión obtenida con simplify y obtenemos el integrando.

Integales definidas

${\displaystyle {\displaystyle \underset{a}{\overset{b}{\int }}f(x)dx}={F(x)|}_a^b=F(b)-F(a)}$

Siendo F(x) el integrando de f(x), es decir dF(x)/dx=f(x)

${\displaystyle {\displaystyle \underset{0}{\overset{\pi }{\int }}{\sin }^2(x)·dx}={\displaystyle \underset{0}{\overset{\pi }{\int }}\frac{1-\cos (2x)}{2}}dx={\frac{1}{2}x-\frac{\sin (2x)}{4}|}_0^{\pi }=\frac{\pi }{2}}$

>> syms x;
>> int(sin(x)^2,0,pi)
ans =pi/2

En este ejemplo, uno o los dos límites de integración respecto de la variable por defecto son simbólicos.

Un cuerpo se mueve a lo largo de una línea recta de acuerdo a la ley v=t³-4t² +5 m/s. Si en el instante t₀=2 s está situado a x₀=4 m del origen. Calcular la posición x del móvil en cualquier instante.

${\displaystyle \begin{array}{l}x-4=\underset{2}{\overset{t}{\int }}(t^3-4t^2+5)dt\\ x=\frac{1}{4}{t}^4-\frac{4}{3}{t}^3+5t+\frac{2}{3}\text{m}\end{array}}$

>> syms t;
>> v=t^3-4*t^2+5;
>> x=int(v,2,t)+4
x =t*(t^2*(t/4 - 4/3) + 5) + 2/3
>> expand(x)
ans =t^4/4 - (4*t^3)/3 + 5*t + 2/3

Integrales de funciones trigonoméricas

Omitimos la constante C de integración en la solución de la integral indefinida

• ${\displaystyle {\displaystyle \int \frac{dx}{\sin x}}}$

${\displaystyle \frac{1}{2}{\displaystyle \int \frac{dx}{\sin \frac{x}{2}\cos \frac{x}{2}}=}\frac{1}{2}{\displaystyle \int \frac{dx}{\tan \frac{x}{2}{\cos }^2\frac{x}{2}}=}{\displaystyle \int \frac{d\left(\tan \frac{x}{2}\right)}{\tan \frac{x}{2}}=}\ln \left|\tan \left(\frac{x}{2}\right)\right|}$

>> syms x;
>> int(1/sin(x))
ans =log(tan(x/2))

• ${\displaystyle {\displaystyle \int \frac{dx}{\cos x}}}$

${\displaystyle {\displaystyle \int \frac{dx}{{\cos }^2\frac{x}{2}-{\sin }^2\frac{x}{2}}=}{\displaystyle \int \frac{dx}{\left(1-{\tan }^2\frac{x}{2}\right){\cos }^2\frac{x}{2}}=2}{\displaystyle \int \frac{d\left(\tan \frac{x}{2}\right)}{\left(1-{\tan }^2\frac{x}{2}\right)}}}$

Llamamos u=tan(x/2)

${\displaystyle 2{\displaystyle \int \frac{du}{1-u^2}}={\displaystyle \int \frac{du}{1+u}}+{\displaystyle \int \frac{du}{1-u}}=\ln \frac{1+u}{1-u}}$

Volviendo a la variable x

${\displaystyle \begin{array}{l}\ln \left|\frac{1+\tan \frac{x}{2}}{1-\tan \frac{x}{2}}\right|=\ln \left|\frac{\cos \frac{x}{2}+\sin \frac{x}{2}}{\cos \frac{x}{2}-\sin \frac{x}{2}}\right|=\ln \left|\frac{\cos \frac{x}{2}\sin \frac{\pi }{4}+\sin \frac{x}{2}\cos \frac{\pi }{4}}{\cos \frac{x}{2}\cos \frac{\pi }{4}-\sin \frac{x}{2}\sin \frac{\pi }{4}}\right|=\ln \left|\tan \left(\frac{x}{2}+\frac{\pi }{4}\right)\right|\\ \ln \left|\frac{\cos \frac{x}{2}+\sin \frac{x}{2}}{\cos \frac{x}{2}-\sin \frac{x}{2}}\right|=\ln \left|\frac{{\left(\cos \frac{x}{2}+\sin \frac{x}{2}\right)}^2}{\left(\cos \frac{x}{2}-\sin \frac{x}{2}\right)\left(\cos \frac{x}{2}+\sin \frac{x}{2}\right)}\right|=\ln \left|\frac{1+\sin x}{\cos x}\right|\end{array}}$

>> int(1/cos(x))
ans =log(1/cos(x)) + log(sin(x) + 1)

• ${\displaystyle {\displaystyle \int {\tan }^{4}x·dx}}$

${\displaystyle \begin{array}{l}{\displaystyle \int {\tan }^{2}x\left(\frac{1}{{\cos }^{2}x}-1\right)}dx=\frac{{\tan }^{3}x}{3}-{\displaystyle \int {\tan }^{2}x·dx=}\frac{{\tan }^{3}x}{3}-{\displaystyle \int \left(\frac{1}{{\cos }^{2}x}-1\right)·dx=}\\ \frac{{\tan }^{3}x}{3}-\tan x+x\end{array}}$

>> int(tan(x)^4)
 ans =x - tan(x) + tan(x)^3/3

• ${\displaystyle {\displaystyle \int \frac{dx}{{\cos }^{4}x}}}$

${\displaystyle {\displaystyle \int \frac{1}{{\cos }^{2}x}}d\left(\tan x\right)={\displaystyle \int \left(1+{\tan }^{2}x\right)}d\left(\tan x\right)=\tan x+\frac{1}{3}{\tan }^{3}x}$

>> int(1/cos(x)^4)
 ans =(sin(x) + 2*cos(x)^2*sin(x))/(3*cos(x)^3)

• ${\displaystyle {\displaystyle \int \frac{dx}{{\sin }^{3}x}}}$

${\displaystyle \begin{array}{l}\frac{1}{8}{\displaystyle \int \frac{dx}{{\sin }^3\left(\frac{x}{2}\right){\cos }^3\left(\frac{x}{2}\right)}}=\frac{1}{8}{\displaystyle \int \frac{dx}{{\tan }^3\left(\frac{x}{2}\right){\cos }^6\left(\frac{x}{2}\right)}}=\frac{1}{8}{\displaystyle \int \frac{{\left(1+{\tan }^2\left(\frac{x}{2}\right)\right)}^2}{{\tan }^3\left(\frac{x}{2}\right){\cos }^2\left(\frac{x}{2}\right)}dx}\\ \frac{1}{8}{\displaystyle \int \left(\frac{1}{{\tan }^3\left(\frac{x}{2}\right)}+\frac{2}{\tan \left(\frac{x}{2}\right)}+\tan \left(\frac{x}{2}\right)\right)\frac{dx}{{\cos }^2\left(\frac{x}{2}\right)}=}\\ \frac{2}{8}{\displaystyle \int \left(\frac{1}{{\tan }^3\left(\frac{x}{2}\right)}+\frac{2}{\tan \left(\frac{x}{2}\right)}+\tan \left(\frac{x}{2}\right)\right)d\left(\tan \left(\frac{x}{2}\right)\right)=}\\ \frac{1}{4}\left(-\frac{1}{2{\tan }^2\left(\frac{x}{2}\right)}+2\ln \left|\tan \left(\frac{x}{2}\right)\right|+\frac{{\tan }^2\left(\frac{x}{2}\right)}{2}\right)=\frac{1}{2}\left(\ln \left|\tan \left(\frac{x}{2}\right)\right|-\frac{\cos x}{{\sin }^{2}x}\right)\end{array}}$

>> int(1/sin(x)^3)
 ans =log(tan(x/2))/2 - cos(x)/(2*sin(x)^2)

• ${\displaystyle {\displaystyle \int \frac{dx}{{\cos }^{3}x}}}$

${\displaystyle {\displaystyle \int \frac{{\sin }^{2}x+{\cos }^{2}x}{{\cos }^{3}x}dx=}{\displaystyle \int \sin x\frac{\sin x}{{\cos }^{3}x}}dx+{\displaystyle \int \frac{dx}{\cos x}}=}$

Integrando por partes la primera integral

${\displaystyle \frac{\sin x}{2{\cos }^{2}x}-\frac{1}{2}{\displaystyle \int \frac{dx}{\cos x}}+{\displaystyle \int \frac{dx}{\cos x}}=\frac{\sin x}{2{\cos }^{2}x}+\frac{1}{2}\ln \left|\tan x+\frac{1}{\cos x}\right|}$

>>  int(1/cos(x)^3)
 ans =log(tan(x/2 + pi/4))/2 + tan(x)/(2*cos(x))

Integración por sustitución

• ${\displaystyle {\displaystyle \int \frac{x}{\sqrt{x^2+1}}dx}}$

Se hace la sustitución, z=x²+1, dz=2x·dx

${\displaystyle \frac{1}{2}{\displaystyle \int \frac{dz}{\sqrt{z}}}=\frac{1}{2}\frac{z^{1/2}}{\frac{1}{2}}=\sqrt{x^2+1}}$

>> int(x/sqrt(x^2+1))
 ans =(x^2 + 1)^(1/2)

• ${\displaystyle {\displaystyle \int \frac{dx}{\cosh x}}}$

${\displaystyle {\displaystyle \int \frac{2}{e^x+e^{-x}}}dx={\displaystyle \int \frac{2e^x}{e^{2x}+1}}dx}$

Se hace la sustitución, z=e^x, dz=e^xdx

${\displaystyle 2{\displaystyle \int \frac{dz}{z^2+1}}=2{\tan }^{-1}z=2{\tan }^{-1}{e}^x}$

>> int(1/cosh(x))
 ans =2*atan(exp(x))

• ${\displaystyle {\displaystyle \int \frac{\sqrt{x^2+1}}{x^2}dx}}$

Se hace la sustitución, x=tant, dx=dt/cos²t

${\displaystyle \begin{array}{l}{\displaystyle \int \frac{\sqrt{{\tan }^{2}t+1}}{{\tan }^{2}t}}\frac{dt}{{\cos }^{2}t}={\displaystyle \int \frac{dt}{{\sin }^{2}t\cos t}}={\displaystyle \int \frac{{\sin }^{2}t+{\cos }^{2}t}{{\sin }^{2}t\cos t}}dt=\\ {\displaystyle \int \frac{dt}{\cos t}}+{\displaystyle \int \frac{\cos t}{{\sin }^{2}t}}dt=\ln \left|\tan t+\frac{1}{\cos t}\right|-\frac{1}{\sin t}=\ln \left|x+\sqrt{x^2+1}\right|-\frac{\sqrt{x^2+1}}{x}\end{array}}$

>> int(sqrt(x^2+1)/x^2)
 ans =asinh(x) - (x^2 + 1)^(1/2)/x

Véase la definición de la función asinh(x)

• ${\displaystyle {\displaystyle \int \sqrt{a^2-x^2}}dx}$

Se hace la sustitución, x=asint, dx=acost·dt

${\displaystyle \begin{array}{l}{\displaystyle \int a\cos t·a\cos t·dt=a^2}{\displaystyle \int {\cos }^{2}t·dt=a^2{\displaystyle \int \frac{1+\cos (2t)}{2}}}dt=\\ \frac{a^2}{2}\left(\frac{1}{2}\sin (2t)+t\right)=\frac{a^2}{2}\left(\sin t·\cos t+t\right)\end{array}}$

Como

${\displaystyle \sin t=\frac{x}{a}\cos t=\frac{\sqrt{a^2-x^2}}{a}}$

Obtenemos

${\displaystyle =\frac{x}{2}\sqrt{a^2-x^2}+\frac{a^2}{2}\arcsin \left(\frac{x}{a}\right)}$

>> int(sqrt(a^2-x^2))
 ans =(x*(a^2 - x^2)^(1/2))/2 - (a^2*log((a^2 - x^2)^(1/2) + x*1i)*1i)/2

• ${\displaystyle {\displaystyle \int \sqrt{a^2+x^2}}dx}$

Se hace la sustitución, x=ax=sinht, dx=acosht·dt

${\displaystyle \begin{array}{l}{\displaystyle \int a\cosh t·a\cosh t·dt=a^2}{\displaystyle \int {\cosh }^{2}t·dt=a^2{\displaystyle \int \frac{1+\cosh (2t)}{2}}}dt=\\ \frac{a^2}{2}\left(\frac{1}{2}\sinh (2t)+t\right)=\frac{a^2}{2}\left(\sinh t·\cosh t+t\right)\end{array}}$

Como

${\displaystyle \begin{array}{l}\sinh t=\frac{x}{a}\cosh t=\frac{\sqrt{a^2+x^2}}{x}\\ e^t=\cosh t+\sinh t=\frac{x+\sqrt{a^2+x^2}}{a}\end{array}}$

Obtenemos

${\displaystyle =\frac{x}{2}\sqrt{a^2+x^2}+\frac{a^2}{2}\ln \left(x+\sqrt{a^2+x^2}\right)}$

>> int(sqrt(a^2+x^2))
 ans =(x*(a^2 + x^2)^(1/2))/2 + (a^2*log(x + (a^2 + x^2)^(1/2)))/2

• ${\displaystyle {\displaystyle \int \sqrt{1-2x-x^2}·dx}}$

Las integrales del tipo

${\displaystyle {\displaystyle \int \sqrt{a{x}^2+bx+c}·dx}}$

Se reducen a integrales de los dos tipos estudiados anteriormente, tal como apreciamos en este ejemplo

${\displaystyle {\displaystyle \int \sqrt{2-{(1+x)}^2}d(1+x)=\frac{1+x}{2}}\sqrt{1-2x-x^2}+\arcsin \left(\frac{1+x}{\sqrt{2}}\right)}$

>> int(sqrt(1-2*x-x^2))
 ans =asin((2^(1/2)*(x + 1))/2) + (x/2 + 1/2)*(- x^2 - 2*x + 1)^(1/2)

Integración por partes

${\displaystyle {\displaystyle \int u·dv=uv-{\displaystyle \int vdu}}}$

Donde u y v son funciones de x

• ${\displaystyle {\displaystyle \int x\sin (2x)dx}}$

u=x, du=dx, dv=sin(2x)dx, v=-cos(2x)/2

${\displaystyle -\frac{1}{2}x\cos (2x)+\frac{1}{2}{\displaystyle \int \cos (2x)dx=}-\frac{1}{2}x\cos (2x)+\frac{1}{4}\sin (2x)}$

>> int(x*sin(2*x))
 ans =sin(2*x)/4 + (x*(2*sin(x)^2 - 1))/2
>> simplify(ans)
ans =sin(2*x)/4 - (x*cos(2*x))/2

• ${\displaystyle {\displaystyle \int e^{2x}\sin (3x)·dx}}$

u=e^2x, du=2e^2x·dx, dv=sin(3x)dx, v=-cos(3x)/3

${\displaystyle \begin{array}{l}{\displaystyle \int e^{2x}\sin (3x)·dx}=-\frac{1}{3}{e}^{2x}\cos (3x)+\frac{2}{3}{\displaystyle \int e^{2x}\cos (3x)dx}\\ {\displaystyle \int e^{2x}\sin (3x)·dx}=-\frac{1}{3}{e}^{2x}\cos (3x)+\frac{2}{3}\left(\frac{1}{3}{e}^{2x}\sin (3x)-\frac{2}{3}{\displaystyle \int e^{2x}\sin (3x)dx}\right)\\ \left(1+\frac{4}{9}\right){\displaystyle \int e^{2x}\sin (3x)·dx}=-\frac{1}{3}{e}^{2x}\cos (3x)+\frac{2}{9}{e}^{2x}\sin (3x)\\ {\displaystyle \int e^{2x}\sin (3x)·dx}=\frac{1}{13}{e}^{2x}\left(-3\cos (3x)+2\sin (3x)\right)\end{array}}$

>> int(exp(2*x)*sin(3*x))
 ans =-(exp(2*x)*(3*cos(3*x) - 2*sin(3*x)))/13

Integración de funciones racionales

${\displaystyle {\displaystyle \int \frac{P(x)}{Q(x)}}dx}$

Donde P(x) y Q(x)) son polinomios, siendo el grado del numerador menor que el grado del denominador.

Si Q(x)) tiene raíces reales r₁, r₂, ... r_n de multiplicidades m₁, m₂, ... m_n

${\displaystyle \begin{array}{l}\frac{P(x)}{Q(x)}=\frac{A_{11}}{(x-r_1)}+\frac{A_{12}}{{(x-r_1)}^2}+\mathrm{...}\frac{A_{1m_1}}{{(x-r_1)}^{m_1}}+\frac{A_{21}}{(x-r_2)}+\frac{A_{22}}{{(x-r_2)}^2}+\mathrm{...}\frac{A_{2m_2}}{{(x-r_2)}^{m_{12}}}+\mathrm{...}\\ \frac{A_{n1}}{(x-r_n)}+\frac{A_{n2}}{{(x-r_n)}^2}+\mathrm{...}\frac{A_{n{m}_n}}{{(x-r_n)}^{m_n}}\end{array}}$

Si Q(x)) tiene raíces complejas a+ib y a-ib
(x-(a+ib))(x-(a-ib))=x²+px+q

${\displaystyle \frac{P(x)}{Q(x)}=\frac{M_{1}x+N_1}{x^2+px+q}+\mathrm{...}\frac{M_{n}x+N_n}{{(x^2+px+q)}^n}}$

• ${\displaystyle {\displaystyle \int \frac{x}{(x-1){(x+1)}^2}dx}}$

${\displaystyle \frac{x}{(x-1){(x+1)}^2}=\frac{A}{x-1}+\frac{B_1}{x+1}+\frac{B_2}{{(x+1)}^2}}$

Se obtiene, A=1/4, B₁=-1/4, B₂=1/2

${\displaystyle \frac{1}{4}{\displaystyle \int \frac{dx}{x-1}}-\frac{1}{4}{\displaystyle \int \frac{dx}{x+1}}+\frac{1}{2}{\displaystyle \int \frac{dx}{{(x+1)}^2}}=\frac{1}{4}\ln \left|x-1\right|-\frac{1}{4}\ln \left|x+1\right|-\frac{1}{2(x+1)}}$

>> int(x/((x-1)*(x+1)^2))
 ans =- atanh(x)/2 - 1/(2*(x + 1))

Véase la definición de la función atanh(x)

• ${\displaystyle {\displaystyle \int \frac{dx}{x^3-1}}}$

${\displaystyle \frac{1}{x^3-1}=\frac{A}{x-1}+\frac{Mx+N}{x^2+x+1}}$

Se obtiene, A=1/3, M=-1/3, N=-2/3

${\displaystyle \begin{array}{l}\frac{1}{3}{\displaystyle \int \frac{dx}{x-1}}-\frac{1}{3}{\displaystyle \int \frac{x+2}{x^2+x+1}dx=}\frac{1}{3}\ln \left|x-1\right|-\frac{1}{3}{\displaystyle \int \frac{4x+8}{{\left(2x+1\right)}^2+3}dx}=\\ \frac{1}{3}\ln \left|x-1\right|-\frac{1}{6}{\displaystyle \int \frac{2x+1}{x^2+x+1}dx}-\frac{1}{3}{\displaystyle \int \frac{6}{{\left(2x+1\right)}^2+3}dx}=\\ \frac{1}{3}\ln \left|x-1\right|-\frac{1}{6}\ln \left|x^2+x+1\right|-\frac{1}{\sqrt{3}}\arctan \left(\frac{2x+1}{\sqrt{3}}\right)\end{array}}$

>> int(1/(x^3-1))
 ans =log(x - 1)/3 + log(x - (3^(1/2)*1i)/2 + 1/2)*((3^(1/2)*1i)/6 - 1/6) - 
log(x + (3^(1/2)*1i)/2 + 1/2)*((3^(1/2)*1i)/6 + 1/6)

Integrales definidas útiles en Física

${\displaystyle \underset{-\infty }{\overset{+\infty }{{\displaystyle \int }}}\exp (-a{x}^2)dx=2\underset{0}{\overset{+\infty }{{\displaystyle \int }}}\exp (-a{x}^2)dx}$

Dibujamos la función y=exp(-αx²), para α=1/2

>> syms x;
>> ezplot(exp(-x^2/2))
>> grid on
>> xlabel('x')
>> ylabel('y')

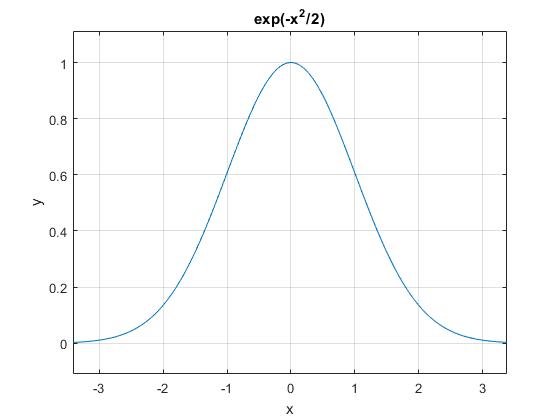
Llamemos I a la integral

${\displaystyle I={\displaystyle \underset{0}{\overset{\infty }{\int }}\exp \left(-\alpha x^2\right)dx}}$

El cuadrado de I es

${\displaystyle I^2={\displaystyle \underset{0}{\overset{\infty }{\int }}{\displaystyle \underset{0}{\overset{\infty }{\int }}\exp \left(-\alpha (x^2+y^2)\right)dxdy}}}$

Cambiamos de coordendas rectangulares a polares, r²=x²+y², dx·dy=rdθ·dr

${\displaystyle I^2={\displaystyle \underset{0}{\overset{\pi /2}{\int }}{\displaystyle \underset{0}{\overset{\infty }{\int }}\exp \left(-\alpha r^2\right)dr·rd\theta }}=\frac{\pi }{2}{\displaystyle \underset{0}{\overset{\infty }{\int }}\exp \left(-\alpha r^2\right)r·dr=\frac{\pi }{4\alpha }}}$

El resultado es

${\displaystyle I={\displaystyle \underset{0}{\overset{\infty }{\int }}\exp \left(-\alpha x^2\right)dx}=\frac{1}{2}\sqrt{\frac{\pi }{\alpha }}}$

La integral no se puede calcular salvo que el parámetro a se declare positivo

>> syms x a;
>> y=exp(-a*x^2);
>> int(y,x,-inf,inf)
Warning: Explicit integral could not be found. 
 
>> clear
>> syms x;
>> syms a positive;
>> y=exp(-a*x^2);
>> int(y,x,-inf,inf)
ans =pi^(1/2)/a^(1/2)

Derivando respecto de α

${\displaystyle {\displaystyle \underset{0}{\overset{\infty }{\int }}{x}^2\exp \left(-\alpha x^2\right)dx}=\frac{1}{4}\sqrt{\frac{\pi }{{\alpha }^3}}}$

Esta integral es inmediata

${\displaystyle {\displaystyle \underset{0}{\overset{\infty }{\int }}x\exp \left(-\alpha x^2\right)dx}=\frac{1}{2\alpha }}$

Derivando respecto de α

${\displaystyle {\displaystyle \underset{0}{\overset{\infty }{\int }}{x}^3\exp \left(-\alpha x^2\right)dx}=\frac{1}{2{\alpha }^2}}$

Ejemplos en el curso de Física

Movimiento rectilíneo

Movimiento curvilíneo

El disco compacto CD

Un cohete de empuje constante

Rozamiento en el bucle

El problema de Kepler

Movimiento de dos cuerpos bajo la fuerza de atracción mutua

Movimiento de dos cuerpos bajo las fuerzas de interacción mutua (gavitatoria y eléctrica)

Series de Fourier

Respuesta del oscilador a una fuerza periódica

Péndulo simple (II)

Un modelo para el coeficiente de restitución

Transformada de Fourier

Las leyes del enfriamiento y calentamiento

La conducción del calor. Ley de Fourier

La conducción del calor en una barra

Ondas térmicas

Distribución de la energía entre las moléculas de un gas ideal

La ley de distribución de las velocidades moleculares

Enfriamiento de un gas

Efusión de un gas

Aproximación al equilibrio de dos gases contenidos en un recinto adiabático y separados por un émbolo (II)

Fómula de Stokes

Movimiento de un imán en un tubo metálico vertical (I)

Elementos de un circuito de corriente alterna

Datos de las olas del mar

Análisis de las alturas y periodos de las olas

Bibliografía

G. Baranenkov, B. Demidovich, V. Efimenko, S. Kogan, G. Lunts, E. Porsheneva, E. Sichova, S. Frolov, R. Shostak, A. Yanpolski. Problemas y ejercicios de Análisis Matemático. Edt. Paraninfo, 1975