La ecuación diferencial del Movimiento Ondulatorio es

${\displaystyle \frac{{\partial }^2\psi }{\partial t^2}=c^2\frac{{\partial }^2\psi }{\partial x^2}}$

Donde c es la velocidad de propagación de las ondas transversales en una cuerda.

${\displaystyle c=\sqrt{\frac{T}{\mu }}}$

• T  es la tensión de la cuerda en N
• μ  es la densidad lineal en kg/m

Condiciones iniciales y de contorno

Para resolver la ecuación diferencial en derivadas parciales que es de segundo orden en x y en t, se precisa especificar dos condiciones inciales: la deformación inicial de la cuerda y la velocidad inicial de cada uno de los puntos de la cuerda

${\displaystyle t=0\{\begin{array}{l}\psi (x\mathrm{,0})={\psi }_0(x)\\ {\frac{\partial \psi (x,t)}{\partial t}|}_{t=0}={\dot{\psi }}_0(x)\end{array}}$

y otras dos condiciones de contorno:

• Un extremo en x=0, es fijo

${\displaystyle \psi (\mathrm{0,}t)=0}$

• El otro extremo en x=l está fijo

${\displaystyle \psi (l,t)=0}$

Pero pueden darse otras posibilidades en los extremos de la cuerda.

Modos de vibración

Para resolver la ecuación diferencial dividimos la solución en producto de dos funciones una dependiente de x y la otra de t.

${\displaystyle \begin{array}{l}\psi (x,t)=\Phi (x)·T(t)\\ \frac{1}{T(t)}\frac{d^{2}T}{d{t}^2}=\frac{c^2}{\Phi (x)}\frac{d^2\Phi }{d{x}^2}=-{\omega }^2\end{array}}$

Como el miembro izquierdo depende solamente de t y el derecho solamente de x, entonces, igualamos ambos a una constante que denominaremos -ω²

${\displaystyle \begin{array}{l}\frac{d^{2}T}{d{t}^2}+{\omega }^2·T=0\\ \frac{d^2\Phi }{d{x}^2}+\frac{{\omega }^2}{c^2}\Phi =0\end{array}}$

Hemos sustituimos una ecuación diferencial en derivadas parciales por dos ecuaciones diferenciales. Ambas ecuaciones tienen soluciones conocidas, ecuación de las oscilaciones libres

${\displaystyle \begin{array}{l}T(t)=A\cos (\omega t)+B\sin (\omega t)\\ \Phi (x)=C\cos \left(\frac{\omega }{c}x\right)+D\sin \left(\frac{\omega }{c}x\right)\end{array}}$

Donde A, B, C y D se determinan a partir de las dos condiciones iniciales y las otras dos de contorno.

Si la cuerda está sujeta por el extremo izquierdo x=0, entonces Φ(0)=0 y C=0. Si está sujeta por el extremo derecho Φ(l)=0, entonces y D no podrá ser nulo en una solución no trivial, sino que

${\displaystyle \sin \left(\frac{\omega }{c}l\right)=0{\omega }_n=n\pi \frac{c}{l}n=\mathrm{1,2,3...}}$

Las frecuencias ω_n se denominan naturales o propias de la cuerda.

${\displaystyle {\Phi }_n(x)=\sin \left(\frac{{\omega }_n}{c}x\right)=\sin \left(n\pi \frac{x}{l}\right)}$

En la figura se muestran los cuatro primeros modos de vibración.

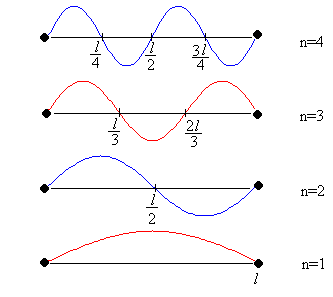
La solución de la ecuación diferencial correspondiente al modo n de vibración de la cuerda es

${\displaystyle {\psi }_n(x,t)={\Phi }_n(x)T_n(t)=\sin \left(n\pi \frac{x}{l}\right)\left(A_n\cos \left(n\pi \frac{c}{l}t\right)+B_n\sin \left(n\pi \frac{c}{l}t\right)\right)}$

donde A_n y B_n son coeficientes que se determinarán a partir de las condiciones iniciales

Superposición

La solución general que satisface las condiciones de contorno Φ(0)=0, y Φ(l)=0, es la superposición

${\displaystyle \begin{array}{l}\psi (x,t)={\displaystyle \sum _{n=1}^{\infty }{\psi }_n(x,t)}={\displaystyle \sum _{n=1}^{\infty }{\Phi }_n(x)\left(A_n\cos \left({\omega }_{n}t\right)+B_n\sin \left({\omega }_{n}t\right)\right)}\\ \psi (x,t)={\displaystyle \sum _{n=1}^{\infty }\sin \left(n\pi \frac{x}{l}\right)\left(A_n\cos \left(n\pi \frac{c}{l}t\right)+B_n\sin \left(n\pi \frac{c}{l}t\right)\right)}\end{array}}$

Esta ecuación describe todos los posibles modos de vibración de la cuerda sujeta por ambos extremos. La vibración particular que experimenta la cuerda está únicamente determinada por las condiciones iniciales, que a su vez determinan los valores de los coeficientes A_n y B_n.

${\displaystyle \begin{array}{l}\psi (x\mathrm{,0})={\psi }_0(x)\to {\displaystyle \sum _{n=1}^{\infty }{A}_n\sin \left(n\pi \frac{x}{l}\right)=}{\psi }_0(x)\\ {\frac{\partial \psi (x,t)}{\partial t}|}_{t=0}={\dot{\psi }}_0(x)\to {\displaystyle \sum _{n=1}^{\infty }n\pi \frac{c}{l}{B}_n\sin \left(n\pi \frac{x}{l}\right)=}{\dot{\psi }}_0(x)\end{array}}$

Teniendo en cuenta el resultado de las integrales

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{l}{\int }}{\sin }^2\left(n\pi \frac{x}{l}\right)}dx=\frac{l}{2}\\ {\displaystyle \underset{0}{\overset{l}{\int }}\sin \left(n\pi \frac{x}{l}\right)\sin \left(m\pi \frac{x}{l}\right)}dx=0m\ne n\end{array}}$

>> syms n x L;
>> assume(n,'integer');
>> int('sin(n*pi*x/L)^2',x,0,L)
ans =L/2 - (L*sin(2*pi*n))/(4*n*pi)
>> simplify(ans)
ans =L/2

Los valores de A_n y B_n se determinan de modo análogo a los coeficientes de un desarrollo en serie de Fourier.

${\displaystyle \begin{array}{l}{A}_n=\frac{2}{l}{\displaystyle \underset{0}{\overset{l}{\int }}{\psi }_0(x)\sin \left(n\pi \frac{x}{l}\right)}dx\\ B_n=\frac{2}{n\pi c}{\displaystyle \underset{0}{\overset{l}{\int }}{\dot{\psi }}_0(x)\sin \left(n\pi \frac{x}{l}\right)}dx\end{array}}$

Cuerda punzada

Perturbación inicial

Una cuerda de longitud l está sometida a una tensión T, tiene una masa μ por unidad de longitud. La cuerda está fija por ambos extremos. La cuerda que está inicialmente en reposo, deformada

${\displaystyle \begin{array}{l}\psi (x\mathrm{,0})=\{\begin{array}{l}\frac{h}{a}x0\le x\le a\\ \frac{h}{l-a}(l-x)a<x\le l\end{array}\\ {\frac{\partial \psi (x,t)}{\partial x}|}_{t=0}=0\end{array}}$

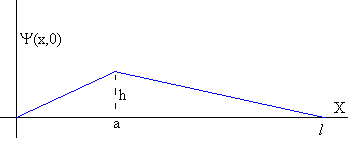
Para calcular la deformación Ψ(x,t) de la cuerda en cualquier punto x y en cualquier instante t, primero calculamos los coeficientes A_n. Los coeficientes B_n=0, son nulos.

${\displaystyle \begin{array}{l}{A}_n=\frac{2}{l}{\displaystyle \underset{0}{\overset{l}{\int }}{\psi }_0(x)\sin \left(n\pi \frac{x}{l}\right)}dx=\\ \frac{2}{l}\left({\displaystyle \underset{0}{\overset{a}{\int }}\frac{h}{a}x\sin \left(n\pi \frac{x}{l}\right)}dx+{\displaystyle \underset{a}{\overset{l}{\int }}\frac{h}{l-a}(l-x)\sin \left(n\pi \frac{x}{l}\right)}dx\right)\\ =\frac{2h{l}^2}{n^2{\pi }^{2}a(l-a)}\sin \left(n\pi \frac{a}{l}\right)\end{array}}$

>> syms x h a L n;
>> assume(n,'integer')
>> an=2*(int('x*sin(n*pi*x/L)',x,0,a)*h/a+
int('(L-x)*sin(n*pi*x/L)',x,a,L)*h/(L-a))/L;
>> simplify(an)
ans =(2*L^2*h*sin((pi*a*n)/L))/(a*n^2*pi^2*(L - a))

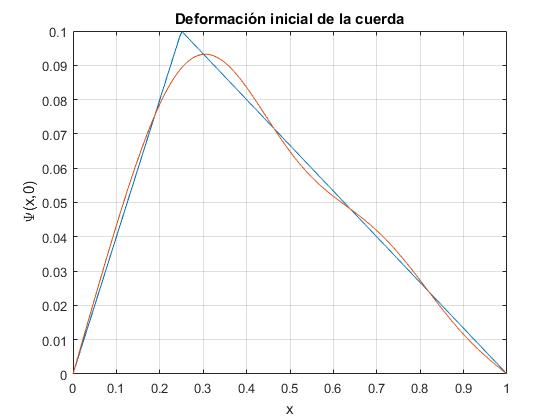
Aproximamos la deformación inicial de la cuerda Ψ(x,0) con los primeros cinco términos del desarrollo en serie

L=1; %longitud de la cuerda
h=0.1; %deformación máxima
a=L/4; %punto de máxima deformación
x=linspace(0,L,200);
y=(h*x/a).*(heaviside(x)-heaviside(x-a))
+(h*(L-x)/(L-a)).*(heaviside(x-a)-heaviside(x-L));
yy=zeros(1,length(x));
for n=1:5; %aproxima con cinco términos
    yy=yy+(2*h*L^2/(pi^2*a*(L-a)))*sin(n*pi*a/L)*sin(n*pi*x/L)/n^2;
end
plot(x,y,x,yy)
xlabel('x')
ylabel('\Psi(x,0)')
title('Deformación inicial de la cuerda')
grid on

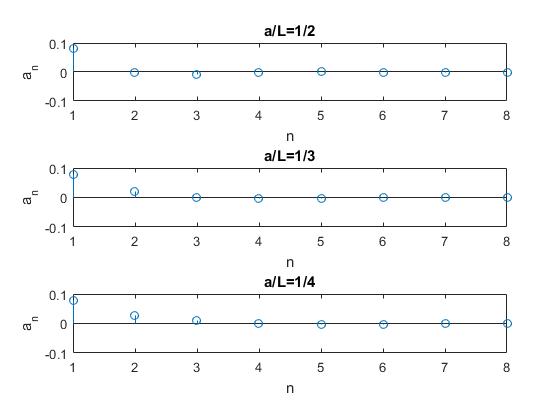
Representamos los primeros coeficientes A_n para tres valores del cociente z=a/l: 1/2, 1/3 y 1/4

${\displaystyle A_n=\frac{2h}{n^2{\pi }^{2}z\left(1-z\right)}\sin \left(n\pi z\right)}$

h=0.1; %deformación máxima
an=@(n,z) 2*h*sin(n*pi*z)./(pi^2*z*(1-z)*n.^2);

subplot(3,1,1)
stem(an(1:8,1/2))
xlabel('n');
ylabel('a_n')
title('L/a=1/2')

subplot(3,1,2)
stem(an(1:8,1/3))
xlabel('n');
ylabel('a_n')
title('L/a=1/3')

subplot(3,1,3)
stem(an(1:8,1/4))
xlabel('n');
ylabel('a_n')
title('L/a=1/4')

>> an(1:8,1/2)
ans =0.0811   0.0000  -0.0090  -0.0000   0.0032   0.0000  -0.0017  -0.0000
>> an(1:8,1/3)
ans =0.0790   0.0197   0.0000  -0.0049  -0.0032  -0.0000   0.0016   0.0012
>> an(1:8,1/4)
ans =0.0764   0.0270   0.0085   0.0000  -0.0031  -0.0030  -0.0016  -0.0000

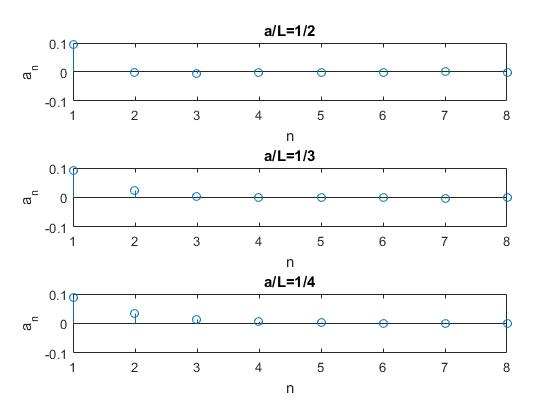
• Cuando a/l=1/2, A₂, A₄, A₆... son nulos
• Cuando a/l=1/3, A₃, A₆, ... son nulos
• Cuando a/l=1/4, A₄, A₈, ... son nulos

Propagación

${\displaystyle \psi (x,t)=\frac{2h{l}^2}{{\pi }^{2}a(l-a)}{\displaystyle \sum _{n=1}^{\infty }\frac{1}{n^2}}\sin \left(n\pi \frac{a}{l}\right)\sin \left(n\pi \frac{x}{l}\right)\cos \left(n\pi \frac{ct}{l}\right)}$

Actividades

La cuerda se desplaza h desde la posición a, tal como se indica en la figura

Se introduce

• La posición a de máximo desplazamiento inicial de la cuerda, en el control titulado Cociente a/l
• Se ha fijado el máximo desplazamiento h=0.1, la longitud de la cuerda l=1 y la velocidad de propagación de las ondas en la cuerda c=1

Se pulsa el botón titulado Nuevo

Se suelta la cuerda y se observa su movimiento, en la parte superior se proporciona el dato del tiempo t

Cuerda pulsada

Perturbación inicial

Una posible representación de la perturbación inicial de la cuerda cuando se actúa con el dedo, en una guitarra o en un arpa sería la siguiente

${\displaystyle $ \begin{array}{l}\psi (x\mathrm{,0})=\{\begin{array}{l}h\frac{x}{a-w}0<x<a-w\\ ha-w<x<a+w\\ h\frac{l-x}{l-(a+w)}x>a+w\end{array}\\ {\frac{\partial \psi (x,t)}{\partial t}|}_{t=0}=0\end{array}$}$

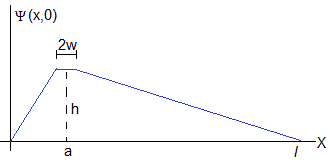
Los coeficientes B_n=0. Calculamos los coeficientes A_n

${\displaystyle \begin{array}{l}{A}_n=\frac{2}{l}{\displaystyle \underset{0}{\overset{l}{\int }}\psi (x\mathrm{,0})\sin \left(n\pi \frac{x}{l}\right)}dx=\\ \frac{2}{l}\left(\begin{array}{l}{\displaystyle \underset{0}{\overset{a-w}{\int }}\frac{h}{a-w}}x\sin \left(n\pi \frac{x}{l}\right)dx+{\displaystyle \underset{a-w}{\overset{a+w}{\int }}h}\sin \left(n\pi \frac{x}{l}\right)dx+\\ {\displaystyle \underset{a+w}{\overset{l}{\int }}\frac{h}{l-a-w}}(l-x)\sin \left(n\pi \frac{x}{l}\right)dx\end{array}\right)\\ =\frac{2hl}{n^2{\pi }^2}\left(\frac{\sin \left(n\pi \frac{a-w}{l}\right)}{a-w}+\frac{\sin \left(n\pi \frac{a+w}{l}\right)}{l-(a+w)}\right)\end{array}}$

Cuando w=0, comprobamos que obtenemos la misma expresión para A_n que en el caso anterior de la cuerda punzada

L=1; %longitud de la cuerda
h=0.1; %deformación máxima
a=L/4; %punto de máxima deformación
w=0.1; %anchura 2w
x=linspace(0,L,200);
y=(h*x/(a-w)).*(heaviside(x)-heaviside(x-a+w))+h*(heaviside(x-a+w)-
heaviside(x-a-w))+(h*(L-x)/(L-a-w)).*(heaviside(x-a-w)-heaviside(x-L));
yy=zeros(1,length(x));
for n=1:10; %aproxima con diez términos
    yy=yy+2*h*L*(sin(n*pi*(a-w)/L)/(a-w)+sin(n*pi*(a+w)/L)/(L-a-w))
*sin(n*pi*x/L)/(pi^2*n^2);
end
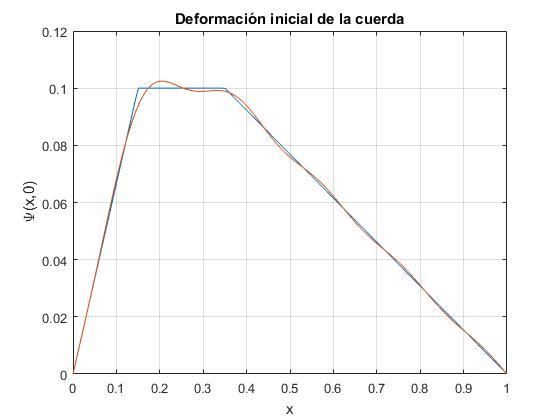
plot(x,y,x,yy)
xlabel('x')
ylabel('\Psi(x,0)')
title('Deformación inicial de la cuerda')
grid on

Representamos los primeros coeficientes B_n para tres valores del cociente z=a/l: 1/2, 1/3 y 1/4

h=0.1; %deformación máxima
w=0.1; %anchura 2w
an=@(n,z) 2*h*(sin(n*pi*(z-w))/(z-w)+sin(n*pi*(z+w))/(1-z-w))./(pi^2*n.^2);

subplot(3,1,1)
stem(an(1:8,1/2))
xlabel('n');
ylabel('a_n')
title('a/L=1/2')

subplot(3,1,2)
stem(an(1:8,1/3))
xlabel('n');
ylabel('a_n')
title('a/L=1/3')

subplot(3,1,3)
stem(an(1:8,1/4))
xlabel('n');
ylabel('a_n')
title('a/L=1/4')

>> an(1:8,1/2)
ans =0.0964   0.0000  -0.0066  -0.0000   0.0000  -0.0000   0.0012   0.0000
>> an(1:8,1/3)
ans =0.0931   0.0252   0.0046  -0.0005  -0.0010  -0.0013  -0.0017  -0.0011
>> an(1:8,1/4)
ans =0.0891   0.0336   0.0143   0.0062   0.0029   0.0014   0.0002  -0.0010

Propagación

${\displaystyle \psi (x,t)=\frac{2hl}{{\pi }^2}{\displaystyle \sum _{n=1}^{\infty }\frac{1}{n^2}\left(\frac{\sin \left(n\pi \frac{a-w}{l}\right)}{a-w}+\frac{\sin \left(n\pi \frac{a+w}{l}\right)}{l-(a+w)}\right)}\sin \left(n\pi \frac{x}{l}\right)\sin \left(n\pi \frac{c}{l}t\right)}$

Cuerda percutida

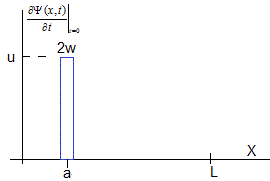
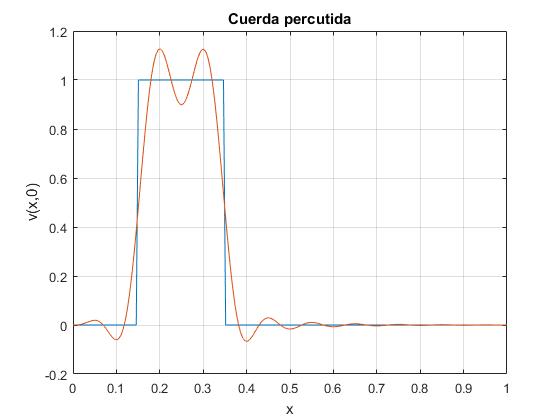
En el caso del piano, al instante t=0, la cuerda está inmóvil en su posición inicial sin perturbar, Ψ(x,0)=0. Se golpea con un martillo de ancho 2w<<L situado entre las abscisas x=a-w y x=a+w que comunica un impulso inicial a este segmento de cuerda. En estas condiciones, la velocidad de cada punto de la cuerda al instante t=0 esta dada por la función de la figura

${\displaystyle \begin{array}{l}{\frac{\partial \psi (x,t)}{\partial t}|}_{t=0}=\{\begin{array}{l}0x<a-wx>a+w\\ ua-w\le x\le a+w\end{array}\\ \psi (x\mathrm{,0})=0\end{array}}$

Los coeficientes A_n=0, son nulos y los coeficientes B_n se calculan

${\displaystyle \begin{array}{l}{B}_n=\frac{2}{n\pi c}{\displaystyle \underset{0}{\overset{l}{\int }}{\frac{\partial \psi (x,t)}{\partial t}|}_{t=0}\sin \left(n\pi \frac{x}{l}\right)}dx=\\ \frac{2}{n\pi c}{\displaystyle \underset{a-w}{\overset{a+w}{\int }}u\sin \left(n\pi \frac{x}{l}\right)dx=\frac{4ul}{n^2{\pi }^{2}c}}\sin \left(n\pi \frac{w}{l}\right)\sin \left(n\pi \frac{a}{l}\right)\end{array}}$

Aproximamos el pulso rectangular tomando 20 términos del desarrollo en serie

${\displaystyle \begin{array}{l}{\frac{\partial \psi (x,t)}{\partial t}|}_{t=0}=\frac{\pi c}{l}{\displaystyle \sum _{n=1}^{\infty }n{B}_n\sin \left(n\pi \frac{x}{l}\right)}=\\ \frac{4u}{\pi }{\displaystyle \sum _{n=1}^{\infty }\frac{1}{n}\sin \left(n\pi \frac{w}{l}\right)\sin \left(n\pi \frac{a}{l}\right)\sin \left(n\pi \frac{x}{l}\right)}\end{array}}$

L=1; %longitud de la cuerda
u=1; %velocidad
a=L/4; 
w=0.1; %anchura es 2w
x=linspace(0,L,200);
y=u*(heaviside(x-a+w)-heaviside(x-a-w));
yy=zeros(1,length(x));
for n=1:20; %aproxima con veinte términos
    yy=yy+4*u*sin(n*pi*w/L)*sin(n*pi*a/L)*sin(n*pi*x/L)/(n*pi);
end
plot(x,y,x,yy)
xlabel('x')
ylabel('v(x,0)')
title('Cuerda percutida')
grid on

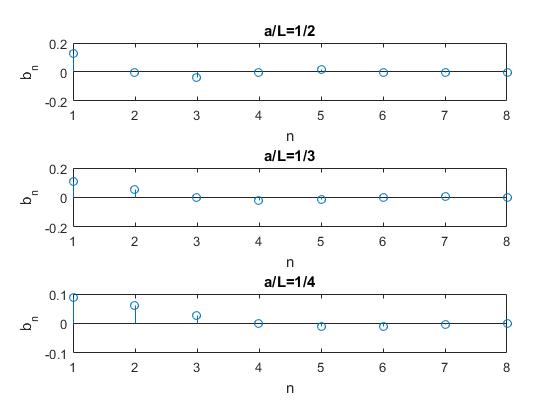
Representamos los primeros coeficientes B_n para tres valores del cociente z=a/l: 1/2, 1/3 y 1/4

u=1; %velocidad
w=0.1; %anchura 2w
bn=@(n,z) 4*u*(sin(n*pi*w).*sin(n*pi*z))./(n.^2*pi^2);
subplot(3,1,1)
stem(bn(1:8,1/2))
xlabel('n');
ylabel('b_n')
title('a/L=1/2')

subplot(3,1,2)
stem(bn(1:8,1/3))
xlabel('n');
ylabel('b_n')
title('a/L=1/3')

subplot(3,1,3)
stem(bn(1:8,1/4))
xlabel('n');
ylabel('b_n')
title('a/L=1/4')

>> bn(1:8,1/2)
ans =0.1252   0.0000  -0.0364  -0.0000   0.0162   0.0000  -0.0067  -0.0000
>> bn(1:8,1/3)
ans =0.1085   0.0516   0.0000  -0.0209  -0.0140  -0.0000   0.0058   0.0032
>> bn(1:8,1/4)
ans =0.0886   0.0596   0.0258   0.0000  -0.0115  -0.0107  -0.0047  -0.0000

B_n se hace nulo cuando na/L es un número entero, 0, 1,2,3.... Por ejemplo, si se golpea la cuerda en la mitad, a=L/2, los coeficientes B_n se hacen nulos para n=2, 4, 6,... Si se golpea la cuerda en, a=L/3, los coeficientes B_n se hacen nulos para n=3, 6, 9,.... La posición a donde se percute la cuerda selecciona los armónicos y sus amplitudes

Propagación

${\displaystyle \psi (x,t)=\frac{4ul}{{\pi }^{2}c}{\displaystyle \sum _{n=1}^{\infty }\frac{1}{n^2}\sin \left(n\pi \frac{w}{l}\right)\sin \left(n\pi \frac{a}{l}\right)}\sin \left(n\pi \frac{x}{l}\right)\sin \left(n\pi \frac{c}{l}t\right)}$

Actividades

La cuerda se percute en la posición a, tal como se indica en la figura

Se introduce

• La posición a, en el control titulado Cociente a/l
• La anchura 2w del percutor, en el control titulado Anchura pulso w
• Se ha fijado la velocidad u=1 del percutor, la longitud de la cuerda l=1 y la velocidad de propagación de las ondas en la cuerda c=0.2

Se pulsa el botón titulado Nuevo

Se percute la cuerda horizontal y en reposo con un dispositivo (rectángulo de color gris) y se observa su movimiento, en la parte superior se proporciona el dato del tiempo t