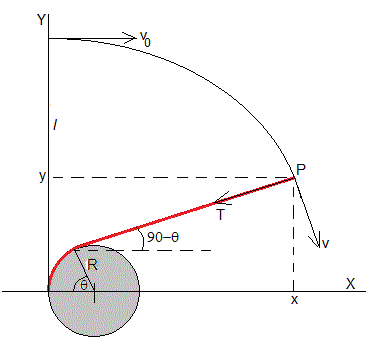
En la figura se muestra la situación inicial de la cuerda de longitud l sin enrollar, tiene la dirección del eje Y, y la partícula cuya posición es (0,l) se lanza con velocidad v₀.

En el instante t, la cuerda se ha enrollado en el tubo de radio R, cubriendo un arco de ángulo θ

La cuerda ejerce una fuerza igual a tensión T sobre la partícula de masa m

Posición y velocidad de la partícula

La posición de la partícula es (x,y).

${\displaystyle \begin{array}{l}\{\begin{array}{l}x=R-R\cos \theta +(l-R\theta )\cos (90-\theta )\\ y=R\sin \theta +(l-R\theta )\sin (90-\theta )\end{array}\\ \{\begin{array}{l}x=R(1-\cos \theta )+(l-R\theta )\sin \theta \\ y=R\sin \theta +(l-R\theta )\cos \theta \end{array}\end{array}}$

Calculamos la pendiente de la recta tangente a la trayectoria en P.

${\displaystyle \begin{array}{l}\frac{dx}{d\theta }=(l-R\theta )\cos \theta \\ \frac{dy}{d\theta }=-(l-R\theta )\sin \theta \end{array}\}\frac{dy}{dx}=-\frac{1}{\tan \theta }}$

La recta tangente es perpendicular a la dirección de la cuerda, tal como se aprecia en la figura. La tensión T y el vector velocidad $\overrightarrow{v}$ o el vector desplazamiento $\overrightarrow{dr}$ son perpendiculares, por lo que la tensión de la cuerda no realiza trabajo alguno. La velocidad de la partícula se mantiene constante e igual a v₀

Las componentes del vector velocidad de la partícula son

${\displaystyle \{\begin{array}{l}\frac{dx}{dt}=\frac{dx}{d\theta }\frac{d\theta }{dt}=(l-R\theta )\cos \theta \frac{d\theta }{dt}\\ \frac{dy}{dt}=\frac{dy}{d\theta }\frac{d\theta }{dt}=-(l-R\theta )\sin \theta \frac{d\theta }{dt}\end{array}}$

El módulo de la velocidad es constante v₀

${\displaystyle \begin{array}{l}{v}_0^2={\left(l-R\theta \right)}^2{\left(\frac{d\theta }{dt}\right)}^2\\ \frac{d\theta }{dt}=\frac{v_0}{l-R\theta }\end{array}}$

Integramos la ecuación diferencial con la condición inicial de que en el instante t=0, θ=0

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{\theta }{\int }}\left(l-R\theta \right)d\theta =v_0{\displaystyle \underset{0}{\overset{t}{\int }}dt}}\\ t=\frac{l\theta -\frac{1}{2}R{\theta }^2}{v_0}\\ \theta =\frac{l}{R}\left(1-\sqrt{1-2\frac{R{v}_{0}t}{l^2}}\right)\end{array}}$

El tiempo total que tarda en enrollarse completamente la cuerda θ=l/R es

${\displaystyle \tau =\frac{1}{2}\frac{l^2}{R{v}_0}}$

En este instante, la partícula toca el tubo

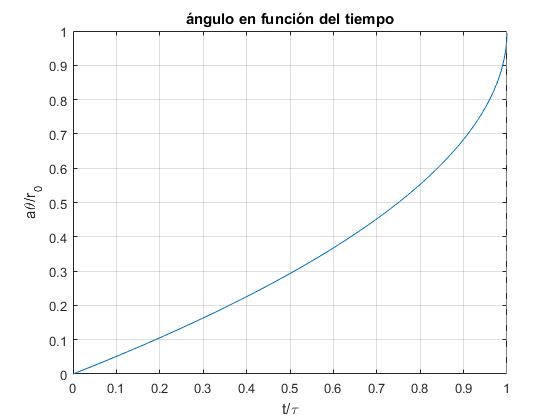
Representamos gráficamente θ o mejor θ·R/l en función de t/τ

${\displaystyle \theta =\frac{l}{R}\left(1-\sqrt{1-\frac{t}{\tau }}\right)}$

f=@(t) 1-sqrt(1-t);
fplot(f,[0,1])
grid on
ylim([0,1])
xlabel('t/\tau')
ylabel('R\theta/l')
title('ángulo en función del tiempo')

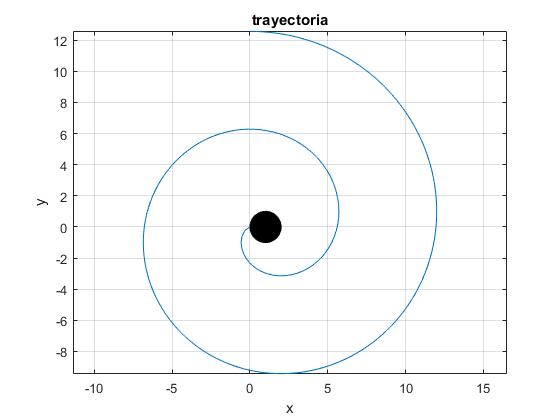
Conocido el ángulo θ en función del tiempo t, obtenemos las coordenadas (x,y) de la partícula en función del tiempo y dibujamos la trayectoria

R=1; %radio del tubo
l=R*4*pi; %longitud de la cuerda
%tubo
t=(0:1:360)*pi/180;
x1=R*cos(t);
y1=R*sin(t);
fill(x1+R,y1,'k')
%trayectoria
tt=linspace(0,1,200);
ang=l*(1-sqrt(1-tt))/R;
x=R*(1-cos(ang))+(l-R*ang).*sin(ang);
y=R*sin(ang)+(l-R*ang).*cos(ang);
hold on
plot(x,y) 
axis equal
grid on
xlabel('x')
ylabel('y')
title('trayectoria')

La tensión T de la cuerda

Conocido dθ/dt, las expresiones de las componentes de la velocidad se simplifican

${\displaystyle \{\begin{array}{l}\frac{dx}{dt}=v_0\cos \theta \\ \frac{dy}{dt}=-v_0\sin \theta \end{array}}$

Derivamos para obtener las componentes de la aceleración

${\displaystyle \{\begin{array}{l}\frac{d^{2}x}{d{t}^2}=-v_0\sin \theta \frac{d\theta }{dt}=-\frac{v_0^2}{l-R\theta }\sin \theta \\ \frac{d^{2}y}{d{t}^2}=-\frac{v_0^2}{l-R\theta }\cos \theta \end{array}}$

El módulo de la aceleración a y la tensión T de la cuerda son, respectivamente

${\displaystyle \begin{array}{l}a=\frac{v_0^2}{l-R\theta }\\ T=ma=\frac{v_0^2}{l-R\theta }\end{array}}$

La tensión T se incrementa sin límite a medida que la partícula se acerca al tubo, θ=l/R, T→∞

Momento angular

El momento angular inicial de la partícula respecto del origen (véase la primera figura), es

L₀=mlv₀. La dirección es el eje Z y el sentido negativo

El momento angular cuando la partícula se encuentra en la posición (x,y) es

${\displaystyle \begin{array}{l}\overrightarrow{L}=m\overrightarrow{r}\times \overrightarrow{v}\\ \overrightarrow{r}=x\widehat{i}+y\widehat{j}\\ v=\frac{dx}{dt}\widehat{i}+\frac{dy}{dt}\widehat{j}\\ \overrightarrow{L}=m\left(x\frac{dy}{dt}-y\frac{dx}{dt}\right)\widehat{k}\end{array}}$

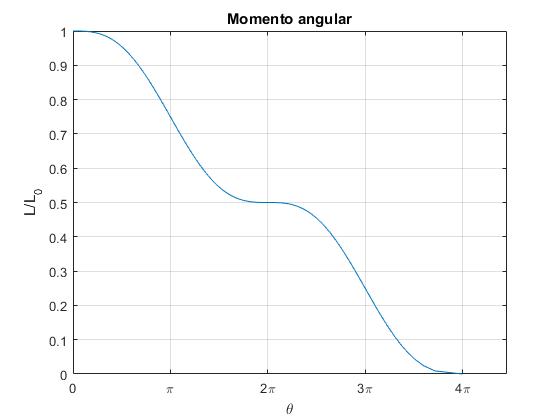
Introduciendo las expresiones de x, y y sus derivadas, el momento angular L tiene la dirección del eje Z, sentido negativo, su módulo es

${\displaystyle L=m{v}_0\left(R\sin \theta +l-R\theta \right)}$

El momento angular L no es constante, ya que la fuerza sobre la partícula T no es central

${\displaystyle \frac{L}{L_0}=1+\left(\sin \theta -\theta \right)\frac{R}{l}}$

R=1; %radio del tubo
l=R*4*pi; %longitud de la cuerda
tt=linspace(0,1,200);
ang=l*(1-sqrt(1-tt))/R;
L=1+(sin(ang)-ang)*R/l;
plot(ang,L)
grid on
set(gca,'XTick',0:pi:4*pi)
set(gca,'XTickLabel',{'0','\pi','2\pi','3\pi','4\pi'})

xlabel('\theta')
ylabel('L/L_0')
title('Momento angular')

Actividades

Se introduce

• El cociente l/R en unidades de π en el control titulado l/R
• Se ha fijado el radio del cilindro en R=1

Se pulsa el botón titulado Nuevo

Observamos el movimiento de la partícula hasta que la cuerda se enrolla completamente en el cilindro

En la parte superior izquierda, se proporcionan los datos de:

• El tiempo t. Cuando la cuerda se enrolla completamente en el cilindro, obtenemos el tiempo total τ
• La posición (x,y) de la partícula
• La parte de la cuerda que se enrolla en el cilindro, es decir, el arco que subtiende un ángulo θ. Cuando la cuerda se ha enrollado completamente en el cilindro θ=l/R

Referencias

O.L. de Lange, J. Pierrus. Solved Problems in Classical Mechanics. Analytical and numerical solutions with comments. Oxford University Press (2010). Questions 6.17, pp. 147-151