Supongamos una varilla metálica de longitud L, conectada por sus extremos a dos focos de calor a temperaturas T_a y T_b respectivamente. Sea T₀ la temperatura inicial de la varilla cuando se conectan los focos a los extremos de la varilla.

Para calcular la temperatura T(x,t) en un punto x de la varilla y en un isntante t, resolvemos la ecuación de la conducción del calor

${\displaystyle \frac{1}{\alpha }\frac{\partial T}{\partial t}=\frac{{\partial }^{2}T}{\partial x^2}0<x<Lt>0}$

con las siguientes condiciones de contorno: T(0,t)=T_a, T(L,t)=T_b

y la temperatura inicial T(x,0)=T₀ constante en todos los puntos de la varilla

El estado estacionario

Al cabo de cierto tiempo, teóricamente infinito, que en la práctica depende del tipo de material que empleamos, se establece un estado estacionario en el que la temperatura de cada punto de la varilla no varía con el tiempo.

${\displaystyle \begin{array}{l}\frac{{\partial }^{2}T}{\partial x^2}=0\\ T(x)=Ax+B\end{array}}$

donde A y B se determinan a partir de las condiciones de contorno en x=0

T(0)=T_a. El coeficiente B=T_a

y en x=L, T(L)=T_b

${\displaystyle T(x,\infty )=T_a+\frac{T_b-T_a}{L}x}$

Solución de la ecuación de la conducción del calor

Definimos la función u(x,t)=T(x,t)-T(x,∞), en términos de esta nueva función, la ecuación de la conducción del calor se escibe,

${\displaystyle \frac{1}{\alpha }\frac{\partial u}{\partial t}=\frac{{\partial }^{2}u}{\partial x^2}0<x<Lt>0}$

Condición inicial

u(x,0)=T(x,0)-T(x,∞)

${\displaystyle u(x\mathrm{,0})=T_0-T_a-(T_b-T_a)\frac{x}{L}}$

Condiciones de contorno

En el extremo izquierdo, x=0

u(0,t)=T(0,t)-T(0,∞)

u(0,t)=T_a-T_a=0

En el extremo derecho, x=L

u(L,t)=T(L,t)-T(L,∞)

u(L,t)=T_b-T_b=0

Variables separadas

Buscamos una solución de la forma u(x,t)=F(x)·G(t), variables separadas

${\displaystyle \frac{1}{\alpha }\frac{1}{G(t)}\frac{dG(t)}{dt}=\frac{1}{F(x)}\frac{d^{2}F(x)}{d{x}^2}=-{\omega }^2}$

A la izquierda, tenemos una función que depende solo de t, a la derecha, otra función que solamente depende de x, ambas son iguales a una constante que denominamos -ω²

Integramos la primera ecuación diferencial

${\displaystyle \begin{array}{l}\frac{dG(t)}{dt}+\alpha {\omega }^{2}G(t)=0\\ G(t)=G(0)·\exp \left(-\alpha {\omega }^{2}t\right)\end{array}}$

Integramos la segunda ecuación diferencial

${\displaystyle \frac{d^{2}F(x)}{d{x}^2}+{\omega }^{2}F(x)=0}$

Es una ecuación diferencial similar a la de un Movimiento Armónico Simple, cuya solución es F(x)=Asin(ωx)+Bcos(ωx)

Solución general

• En el extremo izquierdo de la varilla x=0, u(0, t)=0,

F(0)=0, por lo que B=0

• En el extremo derecho de la varilla x=L, u(L, t)=0

F(L)=Asin(ωL)=0, ωL=nπ, n=1,2,3...

La solución completa u(x,t) es la superposición de los productos de las funciones F_n(x)·G_n(x) para cada ω_n=nπ/L

${\displaystyle u(x,t)={\displaystyle \sum _{n=1}^{\infty }{a}_n\sin \left({\omega }_{n}x\right)\exp \left(-\alpha {\omega }_n^{2}t\right)}}$

Coeficientes a_n

Solamente, queda por determinar los coeficientes A_n, identificando la solución para t=0 con la condición inicial u(x,0)

${\displaystyle u(x,0)={\displaystyle \sum _{n=1}^{\infty }{a}_n}\sin \left(\frac{n\pi }{L}x\right)u(x,0)=T_0-T_a-\frac{T_b-T_a}{L}x}$

Multiplicamos ambos miembros por sin(mπx/L) e integramos entre 0 y L

${\displaystyle {\displaystyle \underset{0}{\overset{L}{\int }}u(x,0)\sin }\left(\frac{m\pi }{L}x\right)dx={\displaystyle \sum _{n=1}^{\infty }{a}_n}{\displaystyle \underset{\text{0}}{\overset{\text{L}}{\int }}\sin \left(\frac{n\pi }{L}x\right)\sin \left(\frac{m\pi }{L}x\right)}dx}$

Calculamos la integral de la derecha, haciendo el cambio de variable z=πx/L, dz= πdx/L

${\displaystyle $ {\displaystyle \underset{0}{\overset{L}{\int }}\sin \left(n\pi \frac{x}{L}\right)\sin \left(m\pi \frac{x}{L}\right)dx}=\frac{L}{\pi }{\displaystyle \underset{0}{\overset{\pi }{\int }}\sin (nz)\sin (mz)dz}$}$

Integramos dos veces por partes

${\displaystyle \left(1-\frac{n^2}{m^2}\right){\displaystyle \underset{0}{\overset{\pi }{\int }}\sin (nz)\sin (mz)dz}={\frac{1}{m}\sin (mz)\cos (nz)-\frac{n}{m^2}\sin (nz)\cos (mz)|}_0^{\pi }=0}$

Cuando m=n

${\displaystyle {\displaystyle \underset{0}{\overset{\pi }{\int }}{\sin }^2(nz)}dz=\frac{1}{2}{\displaystyle \underset{0}{\overset{\pi }{\int }}\left(1-\cos (2nz)\right)}dz={\frac{1}{2}\left(z-\frac{1}{2n}\sin (2nz)\right)|}_0^{\pi }=\frac{\pi }{2}}$

Calculamos el coeficiente a_n conociendo la función u(x,0)

${\displaystyle a_n=\frac{2}{L}{\displaystyle \underset{0}{\overset{L}{\int }}u(x,0)}\sin \left(n\pi \frac{x}{L}\right)dx}$

Sabiendo que u(x,0)=a+bx, donde a=T₀-T_a y b=-(T_b-T_a)/L

${\displaystyle \begin{array}{l}{a}_n=\frac{2}{L}{\displaystyle \underset{0}{\overset{L}{\int }}\left(a+bx\right)\sin \left(n\pi \frac{x}{L}\right)}dx=\\ {\frac{2}{L}\left\{-a\frac{L}{n\pi }\cos \left(n\pi \frac{x}{L}\right)+b\left(-\frac{xL}{n\pi }\cos \left(n\pi \frac{x}{L}\right)+\frac{L^2}{n^2{\pi }^2}\cos \left(n\pi \frac{x}{L}\right)\right)\right\}|}_0^L=\\ \{\begin{array}{l}\frac{2}{n\pi }\left(2a+bL\right)n\text{impar}\\ -\frac{2bL}{n\pi }n\text{par}\end{array}\end{array}}$

Finalmente,

${\displaystyle a_n=\{\begin{array}{l}\frac{2}{n\pi }(2T_0-T_a-T_b)n\text{ impar}\\ \frac{2}{n\pi }(T_b-T_a)n\text{ par}\end{array}}$

Solución completa

La temperatura en cualquier punto de la varilla x, en un instante t, se compone de la suma de un término proporcional a x y de una serie rápidamente convergente que describe el estado transitorio.

${\displaystyle \begin{array}{l}u(x,t)={\displaystyle \sum _{n=1}^{\infty }{A}_n\sin \left(n\pi \frac{x}{L}\right)\exp \left(-\alpha \frac{n^2{\pi }^2}{L^2}t\right)}\\ T(x,t)=u(x,t)+T(x,\infty )=\\ T_a+(T_b-T_a)\frac{x}{L}+{\displaystyle \sum _{n=1}^{\infty }{A}_n\sin \left(n\pi \frac{x}{L}\right)\exp \left(-\alpha \frac{n^2{\pi }^2}{L^2}t\right)}\end{array}}$

El valor de α=K/(ρc) nos da una medida de la rapidez con la que el sistema alcanza el estado estacionario. Cuanto mayor sea α antes se alcanza el estado estacionario

Ejemplo

Fuente: Koshkin N. I., Shirkévich M. G.. Manual de Física Elemental. Editorial Mir 1975. págs 36, 74-75, 85-86

Creamos la función temperatura, que admite como parámetros: las temperaturas de los extremos de la varilla, Ta y Tb, la temperatura inicial T₀, la longitud L de la varilla, el parámetro 1/α, y el tiempo t en el que queremos calcular la distribución de temperaturas a lo largo de la varilla. Devuelve un vector x de puntos a lo largo de la varilla y sus correspondientes temperturas en un vector T.

function [x,T]=temperatura(Ta,Tb,T0,L,a2,t)
   x=linspace(0,L,100);
   T=zeros(length(x),1);
   if(t==0)
       T=T0;
       return;
   end
   k=zeros(2,1);  
   k(1)=2*(2*T0-(Ta+Tb))/pi;
   k(2)=2*(Tb-Ta)/pi;
   cte=pi*pi/(a2*L^2);
   
   T=Ta+(Tb-Ta)*x/L;
   n=0;
   v=1;
   while(v>0.01)
        for j=1:2
            n=n+1;
            v=exp(-cte*n^2*t);
            T=T+v*k(j)*sin(pi*n*x/L)/n;
        end
   end
end

Una serie infinita tenemos que interrumpirla en algún término de acuerdo con algún criterio. Un posible criterio sería que la exponencial

${\displaystyle \exp \left(-\alpha \frac{n^2{\pi }^2}{L^2}t\right)<0.01}$

sea menor que un valor prefijado, por ejemplo 0.01.

Creamos un script que establece

• La temperatura fija en el extremo izquierdo de la varilla, T_a.
• La temperatura fija en el extremo derecho de la varilla, T_b.
• La temperatura inicial de la varilla, T₀.
• El valor del coeficiente, 1/α
• La longitud de la varilla metálica, L

Defina el vector de los instantes t, en segundos, en el que queremos representar la distribución de temperaturas a lo largo de la varilla.

Llame a la función temperatura y represente mediante el comando plot cada una de las graficas T(x,t) en la misma ventana. Como ejercicio se sugiere, además:

• Comprobar que el régimen estacionario es independiente de la temperatura inicial, solamente depende de la temperatura de los focos frío y caliente.
• Examinar el comportamiento de varillas hechas de distintos materiales, con la misma temperatura inicial y fijas en los extremos.

Ta=100; %temperatura en el extremo izquierdo
Tb=30; %temperatura en el extremo derecho
T0=0; %temperatura inicial de la varilla
alfa=11352; %Coeficiente, 1/alfa del aluminio
L=0.5; % longitud de la varilla

hold on
axis([0 0.5 -5 100]);
for t=[10 100 500,2000]
    [x,T]=temperatura(Ta,Tb,T0,L,alfa,t);
    plot(x,T,'displayName',num2str(t));
end
title('Evolución de la temperatura de una varilla')
xlabel('x')
ylabel('T')
legend('-DynamicLegend','location','northeast')
grid on
hold off 

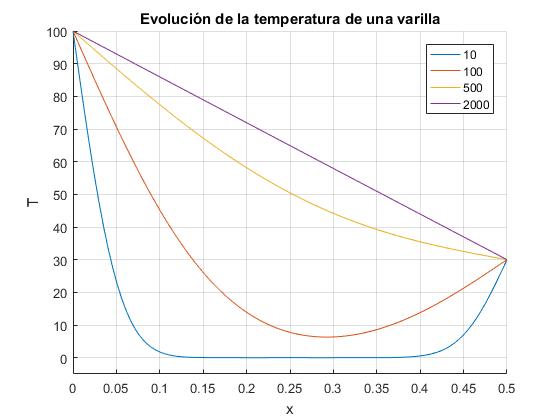
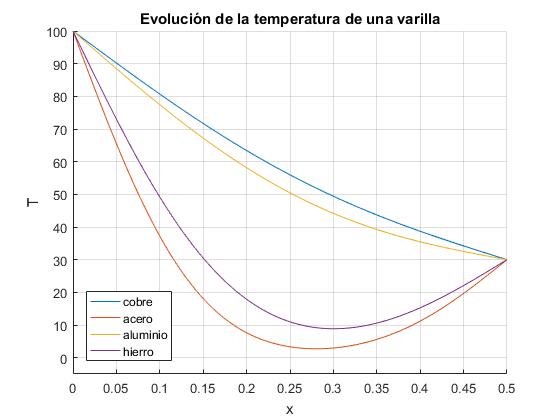
Con este script comparamos el comportamiento de cuatro materiales: cobre, aluminio, hierro y acero en el instante t=500 s. La temperatura inicial de la varilla T₀=0°. La temperatura del extremo x=0 de la varilla es T_a=100° y del extremo x=L, es T_b=30°. La longitud de la varilla es L=0.5 m

Ta=100; %temperatura en el extremo izquierdo
Tb=30; %temperatura en el extremo derecho
T0=0; %temperatura inicial de la varilla
L=0.5; % longitud de la varilla

hold on
axis([0 0.5 -5 100]);
t=500;
for alfa=[8909,79733,11352,47661]; %materiales
    [x,T]=temperatura(Ta,Tb,T0,L,alfa,t);
    plot(x,T);
end
title('Evolución de la temperatura de una varilla')
xlabel('x')
ylabel('T')
legend('cobre','acero','aluminio','hierro','location','southwest')
grid on
hold off 

Referencias

Puig Adam P., Curso teórico-práctico de ecuaciones diferencias aplicado a la Física y Técnica. Biblioteca Matemática (1950), págs. 300-303