Una varilla con una fuente de calor en su extremo
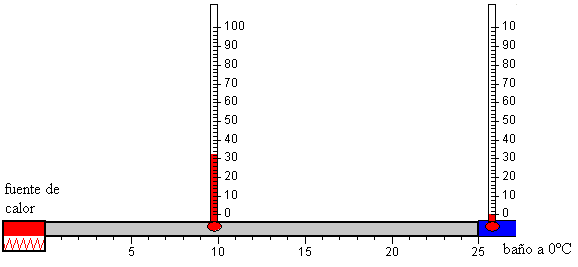
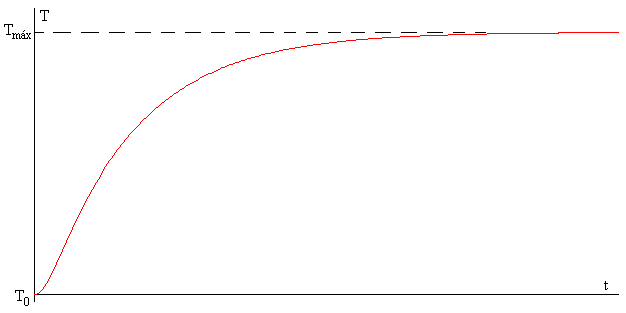
El extremo libre de una varilla metálica de longitud L, está a una temperatura fija T0, por ejemplo, la de un baño que contenga una mezcla de hielo y agua. En el otro extremo, hay una fuente de calor de potencia dQ/dt watios. En un punto x de la varilla se coloca un termómetro. Cuando se conecta la fuente de calor, observamos como la temperatura en dicho punto, va creciendo hasta que toma un valor constante T después de cierto tiempo, teóricamente infinito. Se ha establecido el estado estacionario.
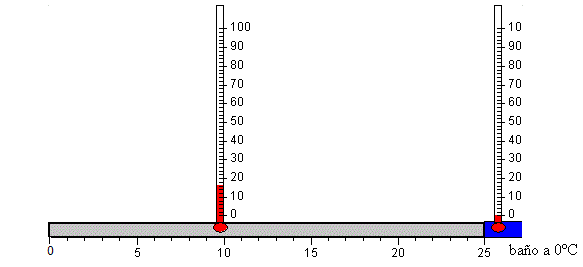
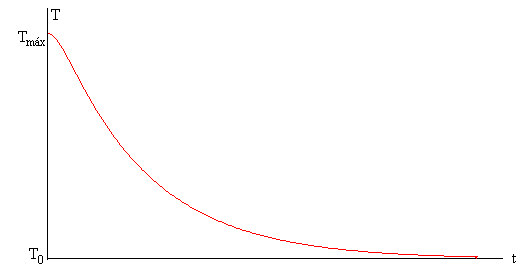
Retiramos la fuente de calor, los dos extremos de la varilla x=0, y x=L están a la temperatura fija T0 del baño. Observamos como la temperatura de dicho punto de la varilla va descendiendo hasta que alcanza la temperatura T0 de baño al cabo de un cierto tiempo, teóricamente infinito.
Se conecta la fuente de calor
El estado estacionario
La ecuación diferencial que describe la conducción térmica
- ρ es la densidad
- c es el calor específico
- K es la conductividad térmica
En el estado estacionario la temperatura de los puntos de la varilla no cambia con el tiempo, ∂T/∂t=0, ∂T/∂x es constante, de acuerdo a la ley de Fourier
El signo menos indica que la temperatura disminuye a lo largo de la varilla: el foco caliente está en x=0, y el foco frío en x=L.
-
S es el área de la sección trasversal de la varilla
-
dQ/dt es la potencia de la fuente de calor colocada en uno de los extremos de la varilla.
-
K una constante característica del material denominada conductividad térmica.
En el estado estacionario t→∞
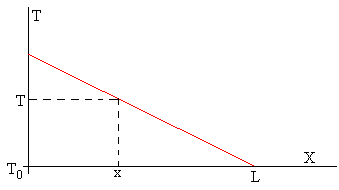
Conociendo la potencia de la fuente de calor, la temperatura fija T0 del extremo x=L y la temperatura T de dicho punto x de la varilla determinamos el coeficiente K de conductividad térmica.
Ejemplo:
-
La potencia de la fuente de calor colocada en un extremo de la varilla es 4.0 W
-
El otro extremo de la varilla, se mantiene a la temperatura de un baño consistente en una mezcla de hielo y agua T0=0ºC
-
La varilla metálica es un cilindro de L=25 cm de longitud y r=5 mm de radio
El termómetro se coloca en la posición x=3 cm, y mide una temperatura máxima de T=53.6º C un tiempo suficientemente grande después de haber conectado la fuente de calor.
Conducción del calor a lo largo de la varilla
Vamos a resolver la ecuación de la conducción del calor
con las condiciones de contorno
y la condición inicial T(x,0)=T0
Solución de la ecuación de la conducción del calor
Definimos la función u(x,t)=T(x,t)-T(x,∞), en términos de esta nueva función, la ecuación de la conducción del calor se escibe,
Condición inicial
u(x,0)=T(x,0)-T(x,∞)
Condiciones de contorno
En el extremo izquierdo, x=0
En el extremo derecho, x=L
u(L,t)=T(L,t)-T(L,∞)
u(L,t)=T0-T0=0
Variables separadas
Buscamos una solución de la forma u(x, t)=F(x)·G(t), variables separadas
Integramos la primera ecuación diferencial
Integramos la segunda ecuación diferencial
Es una ecuación diferencial similar a la de un Movimiento Armónico Simple, cuya solución es F(x)=Acos(ωx)+Bsin(ωx)
Solución general
La condición de contorno en el extremo izquierdo x=0, requiere que la derivada de F(x) con respecto a x, -Aωsin(ωx)+Bωcos(ωx) sea cero en x=0, es decir, que B=0
La condición de contorno en el extremos derecho x=L, requiere que F(x)=Acos(ωx) sea cero en x=L, lo que se cumple para
La solución completa u(x,t) es la superposición de los productos de las funciones Fn(x)·Gn(t) para cada ωn=nπ/L
Coeficientes An
Solamente, queda por determinar los coeficientes An, identificando la solución para t=0 con la condición inicial u(x,0)
Multiplicamos ambos miembros por cos((2m-1)πx/(2L)) e integramos entre 0 y L
Calculamos la integral de la derecha, haciendo el cambio de variable z=πx/L, dz= πdx/L
Integramos dos veces por partes. Comprobamos que la integral es cero cuando m es distinto de n
Cuando m=n, calculamos la integral
Calculamos la integral del miembro izquierdo
Despejamos el coeficiente An
Solución completa
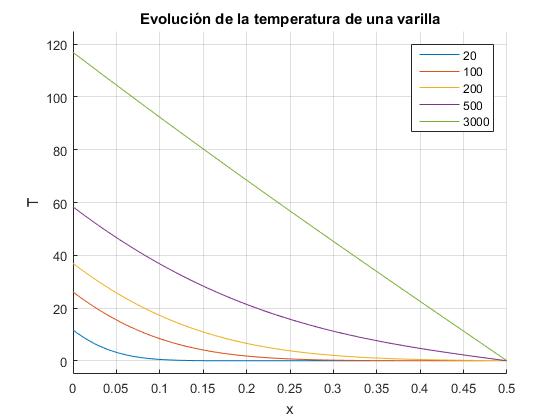
La temperatura en cualquier punto de la varilla x, en un instante t, se compone de la suma de un término proporcional a x y de una serie rápidamente convergente que describe el estado transitorio.
La temperatura en un punto x, alcanza al cabo de un cierto tiempo, teóricamente infinito, un valor constante.
Creamos la función
function [x,T]=temperatura_2(W,T0,L,R,a2,K,t)
x=linspace(eps,L,100);
T=zeros(length(x),1);
if(t==0)
T=T0;
return;
end
T=T0+W*(L-x)/(K*pi*R*R);
n=0;
v=1;
cte=pi*pi/(4*a2*L*L);
factor=8*W*L/(K*pi*R*R*pi*pi);
while(v>0.01)
n=n+1;
v=exp(-cte*(2*n-1)^2*t);
T=T-factor*v*cos(pi*(2*n-1)*x/(2*L))/(2*n-1)^2;
end
end
Una serie infinita tenemos que interrumpirla en algún término de acuerdo con algún criterio. Un posible criterio sería que la exponencial sea menor que un valor prefijado, por ejemplo 0.01.
Creamos un script que establece:
- La potencia de la fuente de calor, W
- La densidad del material, ρ
- El calor específico, c.
- La conductividad térmica, K.
- La temperatura inicial de la varilla y del baño térmico del extremo derecho, T0.
- La longitud de la varilla L y el radio de su sección, R.
Define el vector de los instantes t, en segundos, en el que queremos representar la distribución de temperaturas a lo largo de la varilla.
W=400; %Potencia de la fuente de calor, (W)
T0=0; %Temperatura inicial y fija en el extremo derecho
rho=2700; %Densidad
c=880; %calor específico
K=203.9; %Conductividad térmica
alfa=rho*c/K;
L=0.5; % longitud de la varilla
R=0.05; % radio de la varilla
hold on
axis([0 L -5 125]);
for t=[20 100 200 500 3000]
[x,T]=temperatura_2(W,T0,L,R,alfa,K,t);
plot(x,T,'displayName',num2str(t));
end
title('Evolución de la temperatura de una varilla')
xlabel('x')
ylabel('T')
legend('-DynamicLegend','location','northeast')
grid on
hold off
Se desconecta la fuente de calor. Extremo aislado
Se desconecta la fuente de calor, ponemos el reloj a cero, t=0.
La ecuación que describe la conducción del calor es
Las condiciones de contorno son las siguientes: el extremo izquierdo x=0 está aislado y el extremo derecho x=L se mantiene a temperatura fija T0
La temperatura inicial en los puntos de la varilla es la del estado estacionario de la etapa anterior
El estado estacionario se alcanza después de un tiempo infinito. Todos los puntos de la varilla tienen la misma temperatura del baño situado en el extremo derecho de la varilla T(x,∞)=T0.
Definimos la función u(x,t)=T(x,t)-T(x,∞), en términos de esta nueva función, la ecuación de la conducción del calor, las condición inicial en el instante t=0, y las condiciones de contorno en x=0 y en x=L se escriben
Solución completa
Tenemos las mismas condiciones de contorno que en el ejemplo anterior y la misma condición inicial salvo el signo. La solución de la ecuación de la conducción del calor u(x,t) es idéntica salvo el signo que la precede
La temperatura en cualquier punto x a lo largo de la varilla, en un instante determinado, T(x, t) es una combinación de dos términos, la que corresponde al régimen permanente T(∞, x) más la que corresponde al régimen transitorio.
En la figura se muestra, cómo la temperatura de un punto x de la varilla, va disminuyendo con el tiempo hasta que alcanza la temperatura del baño térmico T0.
Creamos la función
function [x,T]=temperatura_3(W,T0,L,R,a2,K,t)
x=linspace(eps,L,100);
T=zeros(length(x),1);
if(t==0)
T=T0;
return;
end
T=T0;
n=0;
v=1;
cte=pi*pi/(4*a2*L*L);
factor=8*W*L/(K*pi*R*R*pi*pi);
while(v>0.01)
n=n+1;
v=exp(-cte*(2*n-1)^2*t);
T=T+factor*v*cos(pi*(2*n-1)*x/(2*L))/(2*n-1)^2;
end
end
Añadimos los siguientes líneas de código al script anterior
....
figure
hold on
axis([0 L -5 125]);
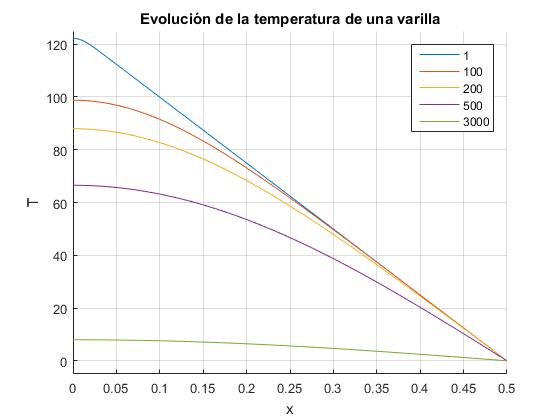
for t=[1 100 200 500 3000]
[x,T]=temperatura_3(W,T0,L,R,alfa,K,t);
plot(x,T,'displayName',num2str(t));
end
title('Evolución de la temperatura de una varilla')
xlabel('x')
ylabel('T')
legend('-DynamicLegend','location','northeast')
grid on
hold off
Referencias
Fox J. N., McMaster R. H., Measurement of the thermal properties of a metal using a relaxation method. Am. J. Phys. 43 (12) December 1975, pp. 1083-1086