Consideremos una esfera de radio R en la cual la distribución inicial de temperaturas y las condiciones de contorno tienen simetría esférica. Las superficies isotérmicas son superficies esféricas concéntricas y la temperatura es una función únicamente de la distancia radial r y del tiempo t.

La esfera se calienta hasta una temperatura uniforme T₀ (distribución inicial de temperaturas T(r, 0)=T₀. En el instante t=0, se sumerge en un recipiente grande de agua a temperatura T_s que es continuamente agitada. La condición de contorno es por tanto, T(R, t)=T_s.

En el estado estacionario, después de un tiempo t→∞, la temperatura final de la esfera será T(r,∞)=T_s, la temperatura del baño térmico.

La ecuación de la conducción del calor apropiada para resolver este problema es

${\displaystyle \begin{array}{l}\frac{1}{\alpha }\frac{\partial T}{\partial t}=\frac{1}{r^2}\frac{\partial }{\partial r}\left(r^2\frac{\partial T}{\partial r}\right)\\ \frac{1}{\alpha }\frac{\partial T}{\partial t}=\frac{2}{r}\frac{\partial T}{\partial r}+\frac{{\partial }^{2}T}{\partial r^2}\end{array}}$

Solución de la ecuación de la conducción del calor

Definimos la función u(r,t)=T(r,t)-T(r,∞), en términos de esta nueva función, la ecuación de la conducción del calor, las condición inicial en el instante t=0, y las condiciones de contorno en r=R se escriben

${\displaystyle \begin{array}{l}\frac{1}{\alpha }\frac{\partial u}{\partial t}=\frac{{\partial }^{2}u}{\partial r^2}+\frac{2}{r}\frac{\partial u}{\partial r}0<r<Rt>0\\ ·\text{contorno}\Rightarrow u(R,t)=0\\ ·\text{inicial}\Rightarrow u(x\mathrm{,0})=T_0-T_s\end{array}}$

Si hacemos la sustitución v(r,t)=r·u(r,t) nos queda la educación diferencial en derivadas parciales

${\displaystyle \frac{\partial v}{\partial t}=\alpha \frac{{\partial }^{2}v}{{\partial }^{2}r}}$

Buscamos soluciones de la forma v(r, t)=F(r)·G(t) (variables separadas)

${\displaystyle \begin{array}{l}\frac{\partial v(r,t)}{\partial t}=\alpha \frac{{\partial }^{2}v(r,t)}{{\partial }^{2}r}\\ \frac{1}{\alpha }\frac{1}{G(t)}\frac{dG(t)}{dt}=\frac{1}{F(r)}\frac{d^{2}F(r)}{d^{2}r}=-{\omega }^2\end{array}}$

Integramos la primara ecuación diferencial

${\displaystyle \begin{array}{l}\frac{dG(t)}{dt}+\alpha {\omega }^{2}G(t)=0\\ G(t)=G(0)·\exp (-\alpha {\omega }^{2}t)\end{array}}$

Integramos la segunda ecuación diferencial

${\displaystyle \frac{d^{2}F(r)}{d^{2}r}+{\omega }^{2}F(r)=0}$

Es una ecuación diferencial similar a la de un Movimiento Armónico Simple. La solución es F(r)=A·sin(ωr)+B·cos(ωr)

En primer lugar, F(0)=0 ya que u(r,t) tiene que ser finito cuando r=0, recuérdese que u(r,t)=v(r,t)/r y v(r, t)=F(r)·G(t). Esto implica que B=0

Condiciones de contorno

u(R,t)=0, por lo que F(R)=A·sin(ωR)=0, es decir, ω_n=nπ/R

La solución v(r,t) es la superposición de los productos F_n(r)·G_n(t). La solución de la ecuación de la conducción del calor r·u(r,t)=v(r,t)

${\displaystyle r·u(r,t)={\displaystyle \sum _{n=1}^{\infty }{A}_n\sin ({\omega }_{n}r)·\exp (-\alpha {\omega }_n^{2}t)}}$

Condición inicial

La condición inicial es u(r,0)=T₀-T_s, que nos permite determinar los coeficientes A_n

${\displaystyle r·u(r\mathrm{,0})={\displaystyle \sum _n{A}_n}\sin \left(\frac{n\pi }{R}r\right)}$

Multiplicamos ambos miembros por sin(mπr/R) e integramos entre 0 y R, para ello, hacemos el cambio de variable z=πr/R, dz=πdr/R

${\displaystyle {\displaystyle \underset{0}{\overset{R}{\int }}r·u(r\mathrm{,0})\sin \left(m\pi \frac{r}{R}\right)dr}={\displaystyle \sum _{n=1}^{\infty }{A}_n{\displaystyle \underset{0}{\overset{R}{\int }}\sin \left(n\pi \frac{r}{R}\right)}}\sin \left(m\pi \frac{r}{R}\right)dr}$

El resultado de la integral del segundo miembro cuando m≠n y cuando m=n es

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{R}{\int }}\sin \left(m\pi \frac{r}{R}\right)\sin \left(n\pi \frac{r}{R}\right)dr}=\frac{R}{\pi }{\displaystyle \underset{0}{\overset{\pi }{\int }}\sin \left(mz\right)\sin \left(nz\right)dz}\\ \left(1-\frac{n^2}{m^2}\right){\displaystyle \underset{0}{\overset{\pi }{\int }}\sin \left(mz\right)\sin \left(nz\right)dz}={-\frac{1}{m}\sin \left(nz\right)\cos \left(mz\right)+\frac{n}{m^2}\cos \left(nz\right)\sin \left(nz\right)|}_0^{\pi }=0\\ {\displaystyle \underset{0}{\overset{\pi }{\int }}{\sin }^2\left(nz\right)dz}=\frac{1}{2}{\displaystyle \underset{0}{\overset{\pi }{\int }}\left(1-\cos \left(2nz\right)\right)dz}=\frac{1}{2}{\left(z-\frac{1}{2n}\sin \left(2nz\right)\right)|}_0^{\pi }=\frac{\pi }{2}\end{array}}$

Despejamos A_n

${\displaystyle A_n=\frac{2}{R}{\displaystyle \underset{0}{\overset{R}{\int }}r·u(r\mathrm{,0})\sin \left(n\pi \frac{r}{R}\right)}dr}$

Teniendo en cuenta que u(r,0)=T₀-T_s y efectuando el cambio de variable z=πr/R

${\displaystyle A_n=\frac{2R}{{\pi }^2}(T_0-T_s){\displaystyle \underset{0}{\overset{\pi }{\int }}z·\sin \text{(}nz\text{)}dz}=\frac{2R}{\pi }(T_0-T_s)\frac{{\left(-1\right)}^{n+1}}{n}}$

Solución completa

La temperatura T(r,t) en cualquier punto a una distancia r del centro de la esfera, en un instante t, se compone de la suma de la temperatura en el estado estacionario T_s y de una serie rápidamente convergente que describe el estado transitorio.

${\displaystyle \begin{array}{l}r·u(r,t)=\frac{2R}{\pi }(T_0-T_s){\displaystyle \sum _{n=1}^{\infty }\frac{{(-1)}^{n+1}}{n}\sin \left(n\pi \frac{r}{R}\right)\exp \left(-\alpha \frac{n^2{\pi }^2}{R^2}t\right)}\\ T(r,t)=u(r,t)+T(r,\infty )=\\ T(r,t)=T_s+\frac{2R}{\pi r}(T_0-T_s){\displaystyle \sum _{n=1}^{\infty }\frac{{(-1)}^{n+1}}{n}\sin \left(n\pi \frac{r}{R}\right)\exp \left(-\alpha \frac{n^2{\pi }^2}{R^2}t\right)}\end{array}}$

Ejemplo

Creamos la función temperatura_1, que admite como parámetros: las temperatura del baño Ts, la temperatura inicial, T0, el radio de la esfera R, el parámetro 1/α y el tiempo t en el que queremos calcular la distribución de temperaturas en la esfera. Devuelve un vector x de puntos a lo largo de la dirección radial y sus correspondientes temperturas en un vector T.

function [x,T]=temperatura_1(Ts,T0,R,a2,t)
   x=linspace(eps,R,100);
    if(t==0)
       T=T0*ones(1,length(x));
       return;
   end  
   T=Ts*ones(1,length(x));
   n=0;
   v=1;
   cte=pi^2/(a2*R^2);
   k=2*R*(T0-Ts)./(pi*x);
    while(v>0.01)
        n=n+1;
        v=exp(-cte*n^2*t);
        T=T+v*(-1)^(n+1)*k.*sin(pi*n*x/R)/n;
   end
end

Una serie infinita tenemos que interrumpirla en algún término de acuerdo con algún criterio. Un posible criterio sería que la exponencial sea menor que un valor prefijado, por ejemplo 0.01. Nos surge otro problema en el origen x=0, se produce una indeterminación 0/0. Calculamos la temperatura en el centro de la esfera mediante la expresión simplificada, o bien, evitar el punto x=0, tomando un punto muy próximo.

Creamos un script que establece

• La temperatura del baño térmico, T_s.
• La temperatura inicial de la esfera, T₀.
• El radio de la esfera, R
• El valor del coeficiente, 1/α que depende del material del que está hecho las esfera

Define el vector de los instantes t, en segundos, en el que queremos representar la distribución de temperaturas a lo largo de la dirección radial.

Llama a la función temperatura_1 y representa mediante el comando plot cada una de las graficas T(x) en la misma ventana.

Ts=100; %Temperatura, baño
T0=0; %Temperatura inicial 
R=0.5; %Radio esfera
alfa=11352; %Coeficiente, 1/alfa

hold on
axis([0 R -5 100]);
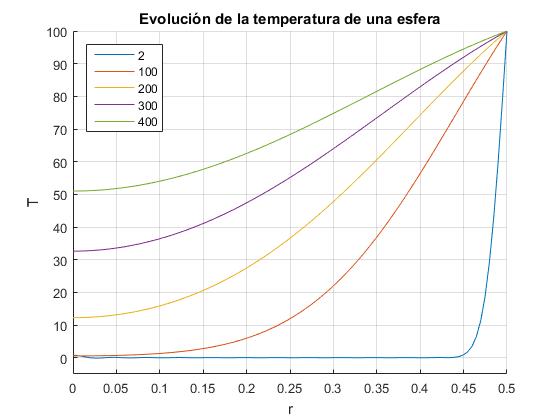
for t=[2 100 200 300 400]
    [x,T]=temperatura_1(Ts,T0,R,alfa,t);
    plot(x,T,'displayName',num2str(t));
end
title('Evolución de la temperatura de una esfera')
xlabel('r')
ylabel('T')
legend('-DynamicLegend','location','northwest')
grid on
hold off 

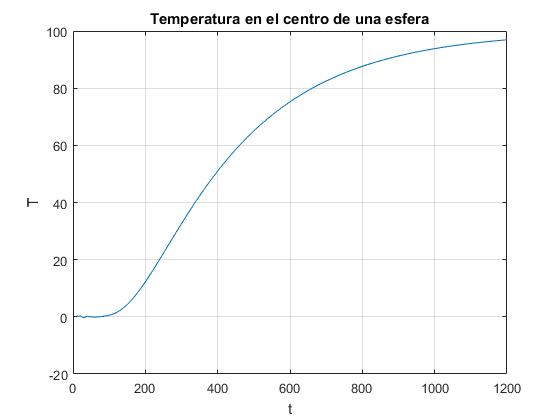
Temperatura en el centro de la esfera

Temperatura en el centro de la esfera cuando r→0

${\displaystyle \underset{r\to 0}{\lim }\frac{\sin \left(nr\frac{\pi }{R}\right)}{nr}=\frac{\pi }{R}}$

en función del tiempo t

${\displaystyle T(\mathrm{0,}t)=T_s+2(T_0-T_s){\displaystyle \sum _{n=1}^{\infty }{(-1)}^{n+1}\exp \left(-\alpha \frac{n^2{\pi }^2}{R^2}t\right)}}$

Representamos la evolución de la temperatura en el centro de una esfera de aluminio de radio R=0.5 m, cuya temperatura inicial es T₀=0°C y se sumerge en un baño de agua hirviendo T_s=100 °C. Como observamos en la gráfica, se tarda un tiempo, alrededor de 100 s, para que la temperatura del centro de la esfera se vaya incrementando apreciablemente, por encima de T₀=0°C

Ts=100; %Temperatura, baño
T0=0; %Temperatura inicial 
R=0.5; %Radio esfera
alfa=11352; %Aluminio, coeficiente, 1/alfa

t=linspace(10,1200,200);
T=Ts*ones(1,length(t));
cte=pi^2/(alfa*R^2);
for i=1:length(t)
    v=1;
    n=0;
    while(v>0.01)
        n=n+1;
        v=exp(-cte*n^2*t(i));
        T(i)=T(i)+v*2*(T0-Ts)*(-1)^(n+1);
    end
end

plot(t,T);
title('Temperatura en el centro de una esfera')
xlabel('t')
ylabel('T')
grid on  

Huevo duro

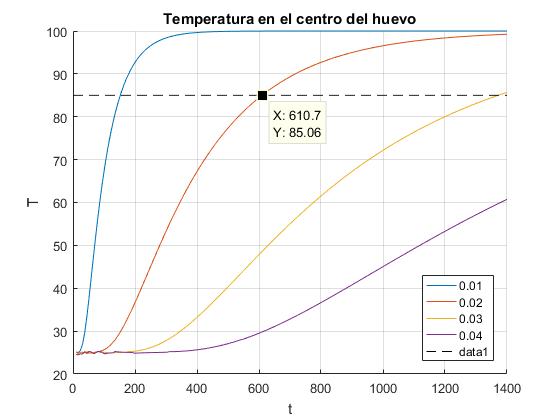
Una aplicación práctica es la estimación del tiempo que tarda un huevo sumergido en agua hirviendo (100 °C) en hacerse duro, tal como se muestra en la fotografía.

En la figura, se muestra la evolución de la temperatura en en el centro de un huevo de radio R supuesto esférico. La temperatura inicial es T₀=25°C y se sumerge en un baño de agua hirviendo T_s=100 °C. El parámetro α=1.53·10^-7 m²/s para la clara y yema del huevo

Ts=100; %Temperatura, baño
T0=25; %Temperatura inicial 

hold on
for R=(1:4)/100 %radios del huevo en cm
    t=linspace(10,1400,200);
    T=Ts*ones(1,length(t));
    cte=1.53e-7*pi^2/R^2;
    for i=1:length(t)
        v=1;
        n=0;
        while(v>0.01)
            n=n+1;
            v=exp(-cte*n^2*t(i));
            T(i)=T(i)+v*2*(T0-Ts)*(-1)^(n+1);
        end
    end
    plot(t,T,'displayName',num2str(R));
end
line([0,1400],[85,85],'lineStyle','--','color','k')
hold off
title('Temperatura en el centro del huevo')
legend('-DynamicLegend','location','southeast')
xlabel('t')
ylabel('T')
grid on  

En la serie infinita, tomamos el primer término n=1 y despreciamos los restantes

${\displaystyle \begin{array}{l}T(\mathrm{0,}t)\approx T_s+2(T_0-T_s)\exp \left(-\alpha \frac{{\pi }^2}{R^2}t\right)\\ t_F=-\frac{R^2}{{\pi }^2\alpha }\log \left(\frac{T_s-T(0)}{2(T_s-T_0)}\right)\end{array}}$

Se considera que un huevo está bien cocido cuando su centro alcanza la temperatura T(0,t)=85°C. Sabiendo que la temperatura inicial del huevo es T₀=25°C y la del baño T_s=100°C, despejamos el tiempo t_F=610 s, para un huevo de radio R=2 cm, que es un valor similar al obtenido en la representación gráfica, donde se han sumado muchos términos de la serie

Referencias

Unsworth J., Duarte F. J. Heat diffusion in a solid sphere and Fourier theory: An elementary practical example. Am. J. Phys. 47 (11) November 1979, pp. 981-983

D Buay, S K Foong, D Kiang, L Kuppan, V H Liew. How long does it take to boil an egg?. Revisited. Eur. J. Phys. 27 (2006) pp. 119-131