Equilibrio térmico

Consideremos dos cuerpos de masas m₁ y m₂, c₁ y c₂ sus calores específicos en J/(kg·K).

Inicialmente cada cuerpo está a una temperatura T₁ y T₂, en recintos adiabáticos separados. En el instante t=0, se elimina la pared de separación y se ponen en contacto. Después de un tiempo, teóricamente infinito, los bloques adquieren una temperatura común de equilibrio T_eq, ya que el calor cedido por el boque caliente Q es absorbido por el bloque más frío (se supone que no hay pérdidas de calor).

${\displaystyle \begin{array}{l}Q=m_1{c}_1(T_{eq}-T_1)Q=m_2{c}_2(T_{eq}-T_2)\\ T_{eq}=\frac{m_1{c}_1{T}_1+m_2{c}_2{T}_2}{m_1{c}_1+m_2{c}_2}\end{array}}$

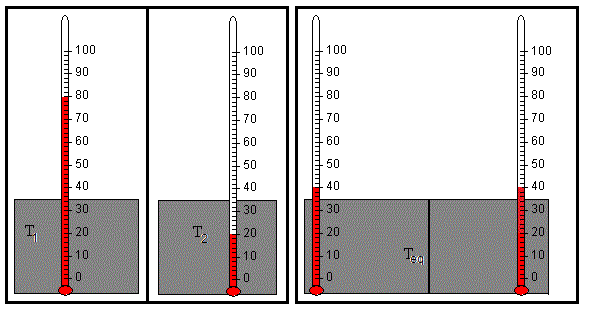
Si los bloques son iguales, hechos del mismo material, la temperatura de equilibrio es T_eq=(T₁+T₂)/2

Evolución hacia el estado de equilibrio

La ecuación diferencial que describe la conducción térmica es

${\displaystyle \frac{\partial T}{\partial t}=\alpha \frac{{\partial }^{2}T}{\partial x^2}\alpha =\frac{K}{\rho c}}$

donde K, es la conductividad térmica, ρ la densidad, y c es la capacidad térmica másica o calor específico del material.

Las condiciones de contorno corresponden a extremos aislados

${\displaystyle {\frac{\partial T(x,t)}{\partial x}|}_{x=0}=0{\frac{\partial T(x,t)}{\partial x}|}_{x=2L}=0}$

En la figura se representa el estado inicial T(x,0): las temperaturas iniciales T₁ y T₂ de los dos bloques de longitud L y el estado estacionario: la temperatura final de equilibrio T(x,∞)=(T₁+T₂)/2 .

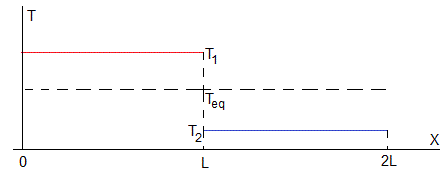
Solución de la ecuación de la conducción del calor

Definimos la función u(x,t)=T(x,t)-T(x,∞), en términos de esta nueva función, la ecuación de la conducción del calor, las condiciones de contorno en x=0 y en x=2L y la condición inicial en el instante t=0, se escriben

${\displaystyle \begin{array}{l}\frac{1}{\alpha }\frac{\partial u}{\partial t}=\frac{{\partial }^{2}u}{\partial x^2}0<x<2Lt>0\\ {·\text{contorno}\Rightarrow \frac{\partial u(x,t)}{\partial x}|}_{x=0}=0{\frac{\partial u(x,t)}{\partial x}|}_{x=2L}=0\\ ·\text{inicial}\Rightarrow u(x\mathrm{,0})=T(x\mathrm{,0})-T_{eq}\end{array}}$

Buscamos una solución de la forma u(x, t)=F(x)·G(t), variables separadas

${\displaystyle \frac{1}{\alpha }\frac{1}{G(t)}\frac{dG(t)}{dt}=\frac{1}{F(x)}\frac{d^{2}F(x)}{d{x}^2}=-{\omega }^2}$

Integramos la primera ecuación diferencial

${\displaystyle \begin{array}{l}\frac{dG(t)}{dt}+\alpha {\omega }^{2}G(t)=0\\ G(t)=G(0)·\exp \left(-\alpha {\omega }^{2}t\right)\end{array}}$

Integramos la segunda ecuación diferencial

${\displaystyle \frac{d^{2}F(x)}{d{x}^2}+{\omega }^{2}F(x)=0}$

Es una ecuación diferencial similar a la de un Movimiento Armónico Simple, cuya solución es F(x)=Acos(ωx)+Bsin(ωx)

Condiciones de contorno

• La condición de contorno en el extremo izquierdo x=0, requiere que la derivada de F(x) con respecto a x, -Aωsin(ωx)+Bωcos(ωx) sea cero en x=0, es decir, que B=0

• La condición de contorno en el extremos derecho x=2L, requiere que la derivada de F(x)=Acos(ωx) sea cero en x=2L, -Aωsin(2ωL)=0, lo que se cumple para 2ωL=nπ

La solución completa u(x,t) es la superposición de los productos de las funciones F_n(x)·G_n(x) para cada ω_n=nπ/(2L)

${\displaystyle u(x,t)={\displaystyle \sum _{n=1}^{\infty }{A}_n\cos \left({\omega }_{n}x\right)\exp \left(-\alpha {\omega }_n^{2}t\right)}}$

Condición inicial

Solamente, queda por determinar los coeficientes A_n, identificando la solución para t=0 con la condición inicial u(x,0)

${\displaystyle u(x,0)={\displaystyle \sum _{n=1}^{\infty }{A}_n\cos \left(n\pi \frac{x}{2L}\right)}u(x,0)=T(x\mathrm{,0})-T_{eq}}$

Multiplicamos ambos miembros por cos(mπx/(2L)) e integramos entre 0 y 2L

${\displaystyle {\displaystyle \underset{0}{\overset{2L}{\int }}u(x,0)\cos }\left(\frac{m\pi }{2L}x\right)dx={\displaystyle \sum _{n=1}^{\infty }{A}_n}{\displaystyle \underset{0}{\overset{\text{2L}}{\int }}\cos \left(\frac{n\pi }{2L}x\right)\cos \left(\frac{m\pi }{2L}x\right)}dx}$

• Integramos el miembro izquierdo

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{2L}{\int }}u(x,0)\cos }\left(\frac{m\pi }{2L}x\right)dx={\displaystyle \underset{0}{\overset{L}{\int }}\left(T_1-T_{eq}\right)\cos }\left(\frac{m\pi }{2L}x\right)dx+\\ {\displaystyle \underset{L}{\overset{2L}{\int }}\left(T_2-T_{eq}\right)\cos }\left(\frac{m\pi }{2L}x\right)dx=\frac{2L}{m\pi }\left(T_1-T_2\right)\sin \left(\frac{m\pi }{2}\right)\end{array}}$

• Para integrar el miembro derecho, hacemos el cambio de variable z=πx/(2L), dz=πdx/(2L)

${\displaystyle {\displaystyle \sum _{n=1}^{\infty }{A}_n}{\displaystyle \underset{0}{\overset{\text{2L}}{\int }}\cos \left(\frac{n\pi }{2L}x\right)\cos \left(\frac{m\pi }{2L}x\right)}dx=\frac{2L}{\pi }{\displaystyle \sum _{n=1}^{\infty }{A}_n}{\displaystyle \underset{0}{\overset{\pi }{\int }}\text{cos(}nz\text{)·cos(}mz\text{)}}dz}$

Integramos por partes

${\displaystyle {\displaystyle \int \text{cos(}nz\text{)·cos(}mz\text{)}dz}=\frac{1}{m}\sin (mz)\cos (nz)+\frac{n}{m}{\displaystyle \int \text{sin(}nz\text{)·sin(}mz\text{)}dz}}$

Volvemos a integrar por partes

${\displaystyle \begin{array}{l}{\displaystyle \int \text{cos(}nz\text{)·cos(}mz\text{)}dz}=\left\{\begin{array}{l}\frac{1}{m}\sin (mz)\cos (nz)\\ +\frac{n}{m}\left(-\frac{1}{m}\cos (mz)\sin (nz)+\frac{n}{m}{\displaystyle \int \text{cos(}nz\text{)·cos(}mz\text{)}dz}\right)\end{array}\right\}\\ \left(1-\frac{n^2}{m^2}\right){\displaystyle \underset{0}{\overset{\pi }{\int }}\text{cos(}nz\text{)·cos(}mz\text{)}dz}={\frac{1}{m}\sin (mz)\text{cos}(nz)-\frac{n}{m^2}\text{cos}(mz)\sin (nz)|}_0^{\pi }\end{array}}$

Obtenemos el siguiente resultado que comprobaremos con Math Symbolic de MATLAB

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{\pi }{\int }}\text{cos(}nz\text{)·cos(}mz\text{)}dz}=0m\ne n\\ {\displaystyle \underset{0}{\overset{\pi }{\int }}{\cos }^{\text{2}}\text{(}nz\text{)·}dz}={\displaystyle \underset{0}{\overset{\pi }{\int }}\frac{1+\cos (2nz)}{2}dz}=\frac{1}{2}{\left(z+\frac{1}{2n}\sin (2nz)\right)}_0^{\pi }=\frac{\pi }{2}\end{array}}$

>> syms t m n;
>> assume(n,'integer');
>> assume(m,'integer');
>>  int('cos(n*t)*cos(m*t)',t,0,pi)
ans =piecewise([m == n | m + n == 0, pi/2], [m ~= n & m + n ~= 0, 0]) 

Teniendo en cuenta estos resultados el miembro de la derecha vale

${\displaystyle {\displaystyle \sum _{n=1}^{\infty }{A}_n}{\displaystyle \underset{0}{\overset{\text{2L}}{\int }}\cos \left(\frac{n\pi }{2L}x\right)\cos \left(\frac{m\pi }{2L}x\right)}dx=L{A}_n}$

Despejamos A_n

${\displaystyle A_n=\frac{2\left(T_1-T_2\right)}{n\pi }\sin \left(\frac{n\pi }{2}\right)\{\begin{array}{l}0n\text{par}\\ \frac{2\left(T_1-T_2\right)}{n\pi }{\left(-1\right)}^{\frac{n-1}{2}}n\text{impar}\end{array}}$

Solución completa

${\displaystyle \begin{array}{l}u(x,t)={\displaystyle \sum _{n=1}^{\infty }{A}_n\cos \left(n\pi \frac{x}{2L}\right)\exp \left(-\alpha \frac{n^2{\pi }^2}{4L^2}t\right)}\\ T(x,t)=u(x,t)+T(x,\infty )\end{array}}$

Así, la temperatura en cualquier punto de la varilla x, en un instante t, se compone de la suma de un término T_eq, la temperatura de equilibrio y de una serie rápidamente convergente que describe el estado transitorio.

${\displaystyle T(x,t)=\frac{T_1+T_2}{2}+\frac{2}{\pi }\left(T_1-T_2\right){\displaystyle \sum _{n=\mathrm{1,3,5...}}^{\infty }\frac{{(-1)}^{\frac{n-1}{2}}}{n}\exp \left(-\alpha \frac{n^2{\pi }^2}{4L^2}t\right)}\cos \left(\frac{n\pi }{2L}x\right)}$

Creamos la función temperatura_6, que admite como parámetros: las temperaturas iniciales T₁ y T₂ de los dos bloques iguales, la longitud L de cada bloque, el parámetro 1/α, y el tiempo t en el que queremos calcular la distribución de temperaturas a lo largo de los bloques de 0 a 2L. Devuelve un vector x de puntos a lo largo de los bloques y sus correspondientes temperturas en un vector T.

function [x,T]=temperatura_6(T1,T2,L,a2,t)
   x=linspace(0,2*L,100);
   T=ones(1,length(x))*(T1+T2)/2; 
   cte=pi^2/(a2*4*L^2);
   n=1;
   v=1;
   while(v>0.01)
        v=exp(-cte*n^2*t);
        T=T+2*(T1-T2)*v*cos(pi*n*x/(2*L))*(-1)^((n-1)/2)/(n*pi);
        n=n+2;
   end
end

Una serie infinita tenemos que interrumpirla en algún término de acuerdo con algún criterio. El que se ha empleado en este programa es el siguiente

${\displaystyle \exp \left(-\alpha \frac{n^2{\pi }^2}{4L^2}t\right)<0.01}$

sea menor que un valor prefijado, por ejemplo 0.01.

Creamos un script que establece

• La temperatura inicial del bloque izquierdo, T₁.
• La temperatura inicial del bloque derecho, T₂.
• El valor del coeficiente, 1/α. Los valores de este parámetro para distintos metales está recogidos en una tabla al final de la página titulada La conducción del calor. Ley de Fourier
• La longitud de los bloques, L

Defina el vector de los instantes t, en segundos, en el que queremos representar la distribución de temperaturas a lo largo de los bloques.

T1=100; %temperatura del bloque izquierdo
T2=30; %temperatura del bloque derecho
alfa=11352; %Coeficiente, 1/alfa del aluminio
L=0.5; % longitud de la varilla
  
hold on
for t=[10 100 200 400, 800]
    [x,T]=temperatura_6(T1,T2,L,alfa,t);
    plot(x,T,'displayName',num2str(t));
end
title('Evolución de la temperatura de los bloques')
xlabel('x')
ylabel('T')
legend('-DynamicLegend','location','northeast')
grid on
hold off 

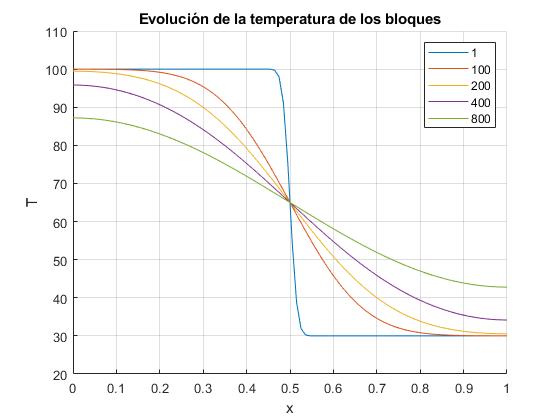
Establecimiento del equilibrio térmico

El equilibrio térmico se alcanza después de un tiempo teóricamente infinito. En la práctica, depende de la sensibilidad de los termómetros empleados para medir la temperatura. Diremos que se ha alcanzado el equilibrio térmico en el instante en el que la diferencia entre la temperatura del extremo izquierdo T(0,t) y la temperatura del extremo derecho T(2L,t) sea menor que un grado

Para calcular este instante, supondremos que después de un tiempo grande t la distribución de temperaturas viene dada esencialmente por el primer término del desarrollo en serie

${\displaystyle T(x,t)\approx \frac{T_1+T_2}{2}+\frac{2}{\pi }\left(T_1-T_2\right)\exp \left(-\alpha \frac{{\pi }^2}{4L^2}t\right)\cos \left(\frac{\pi }{2}x\right)}$

La diferencia de temperatura en los extremos es aproximadamente

${\displaystyle \begin{array}{l}T(\mathrm{0,}t)\approx \frac{T_1+T_2}{2}+\frac{2}{\pi }(T_1-T_2)\exp \left(-\alpha \frac{{\pi }^2}{4L^2}t\right)\hfill \\ T(2L,t)\approx \frac{T_1+T_2}{2}-\frac{2}{\pi }(T_1-T_2)\exp \left(-\alpha \frac{{\pi }^2}{4L^2}t\right)\hfill \\ T(\mathrm{0,}t)-T(2L,t)=\frac{4}{\pi }(T_1-T_2)\exp \left(-\alpha \frac{{\pi }^2}{4L^2}t\right)\hfill \end{array}}$

Añadimos al script la porción de código que calcula el tiempo t en segundos, a partir del cual consideramos que se ha establecido el equilibrio térmico

dT=1; %un grado, la diferencia de temperatura entre los extremos
tFin=-4*L^2*log(dT*pi/(4*L*(T1-T2)))*alfa/pi^2

tFin =   4.3672e+03

Referencias

F M S Lima. Approximate formulae for the thermalization of two blocks in an insulated system. Eur. J. Phys. 35 (2014) 055017