El dispositivo experimental se muestra en la figura. Se establece un gradiente de temperatura poniendo en contacto la parte inferior de la muestra de altura L y espesor w con un recipiente a 0°C que contiene una mezcla de hielo y agua. La parte superior y lateral de la muestra se suponen aisladas.

El gradiente térmico produce un cambio en el índice de refracción de la muestra ya que el índice de refracción depende de la temperatura. Supondremos que α y dn/dT son constantes para el material empleado y para el intervalo de temperaturas a que están sometidos los distintos puntos de la muestra

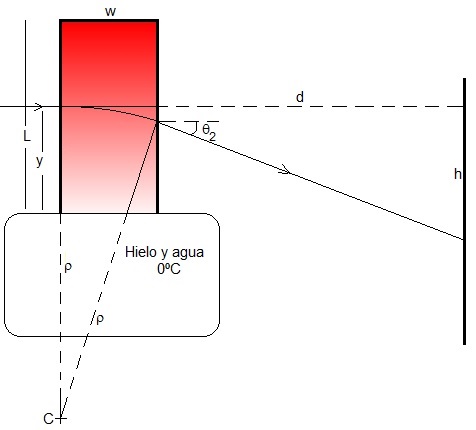
Un haz laser incide sobre una muestra a una distancia y de la parte inferior. Debido a que el índice de refracción varía con la altura n(y) se desvía describiendo un arco de circunferencia de radio ρ dentro de la muestra, impactando a una altura h en una pantalla distante d de la muestra

En la página titulada 'Propagación en un medio no homogéneo (I)' estudiamos que, si en índice de refracción varía solamente con la altura, n(y) entonces.

${\displaystyle \frac{d^{2}y}{d{x}^2}=\frac{1}{n}\frac{dn}{dy}\left(1+{\left(\frac{dy}{dx}\right)}^2\right)}$

Integrando esta ecuación diferencial con la condición inicial

${\displaystyle \tan {\theta }_0={\left(\frac{dy}{dx}\right)}_0}$

Obtuvimos

${\displaystyle {\left(\frac{dy}{dx}\right)}^2=\frac{n^2}{n_0^2}\left(1+{\left(\frac{dy}{dx}\right)}_0^2\right)-1}$

En este caso la incidencia es normal, θ₀=0.

${\displaystyle {\left(\frac{dy}{dx}\right)}^2=\frac{n^2(y)}{n_0^2}-1}$

El radio de curvatura se calcula mediante la fórmula.

${\displaystyle \begin{array}{l}\rho =\frac{{\left(1+{\left(\frac{dy}{dx}\right)}^2\right)}^{3/2}}{\left|\frac{d^{2}y}{d{x}^2}\right|}=\frac{{\left(1+{\left(\frac{dy}{dx}\right)}^2\right)}^{3/2}}{\frac{1}{n}\frac{dn}{dy}\left(1+{\left(\frac{dy}{dx}\right)}^2\right)}=\frac{\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}}{\frac{1}{n}\frac{dn}{dy}}\\ \frac{1}{\rho }\approx \frac{1}{n}\frac{dn}{dy}\end{array}}$

En el que hemos despreciado el término (dy/dx)² frente a la unidad.

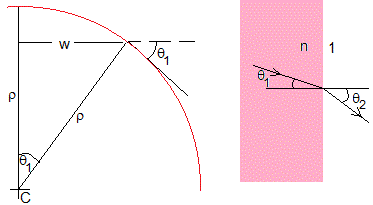
Dentro de la muestra, el haz de luz describe un arco de circunferencia de radio ρ y de longitud, aproximadamente, igual a w, el espesor de la muestra. El ángulo θ₁≈w/ρ=w(dn/dy)/n.

Aplicando la ley de la refracción en la superficie de separación de la muestra y el aire

nsinθ₁=1·sinθ₂

En la figura, más arriba, vemos que tanθ₂=h/d. Cuando los ángulos son pequeños tanθ≈sinθ≈θ, por lo que la ley de la refracción, nθ₁≈θ₂. Despejamos la desviación h, posición del punto de impacto del haz con la pantalla

${\displaystyle h\approx -wd\frac{dn}{dy}=-wd\frac{dn}{dT}\frac{dT}{dy}}$

Conducción del calor en una varilla

En este apartado estudiamos la distribución de temperaturas de la muestra en el instante t, después de haber puesto en contacto la muestra a temperatura ambiente T₀ con el baño a la temperatura T_a=0°C

Supongamos una varilla de longitud L, cuya temperatura inicial es T₀, uno de sus extremos x=0, se mantiene a temperatura constante T_a y el otro extremo x=L está aislado.

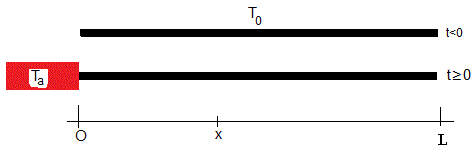
Para calcular la temperatura T(x,t) en un punto x de la varilla y en un instante t, resolvemos la ecuación de la conducción del calor

${\displaystyle \frac{1}{\alpha }\frac{\partial T}{\partial t}=\frac{{\partial }^{2}T}{\partial x^2}0<x<Lt>0}$

La condición de contorno en el extremo izquierdo x=0, es T(0,t)=T_a

La condición de contorno en el extremo derecho x=L, es

${\displaystyle {\frac{\partial T(x,t)}{\partial x}|}_{x=L}=0}$

La condición inicial, es la de una varilla a temperatura uniforme T(x,0)=T₀

El estado estacionario

Al cabo de cierto tiempo, teóricamente infinito, que en la práctica depende del tipo de material que empleamos, se establece un estado estacionario en el que la temperatura de cada punto de la varilla no varía con el tiempo.

${\displaystyle \begin{array}{l}\frac{{\partial }^{2}T}{\partial x^2}=0\\ T(x)=Ax+B\end{array}}$

donde A y B se determinan a partir de las condiciones de contorno en x=0

T(0)=T_a. El coeficiente B=T_a

En x=L, la barra está aislada, la derivada respecto de x es nula, por lo que A=0

La temperatura en el estado estacionario es igual a la del baño, T(x,∞)=T_a

Solución de la ecuación de la conducción del calor

Definimos la función u(x,t)=T(x,t)-T(x,∞), en términos de esta nueva función, la ecuación de la conducción del calor se escibe,

${\displaystyle \frac{1}{\alpha }\frac{\partial u}{\partial t}=\frac{{\partial }^{2}u}{\partial x^2}0<x<Lt>0}$

Condición inicial

u(x,0)=T(x,0)-T(x,∞)=T₀-T_a

Condiciones de contorno

En el extremo izquierdo, x=0

u(0,t)=T(0,t)-T(0,∞)=T_a-T_a=0

En el extremo derecho, x=L

${\displaystyle {\frac{\partial u(x,t)}{\partial x}|}_{x=L}=0}$

Variables separadas

Buscamos una solución de la forma u(x, t)=F(x)·G(t), variables separadas

${\displaystyle \frac{1}{\alpha }\frac{1}{G(t)}\frac{dG(t)}{dt}=\frac{1}{F(x)}\frac{d^{2}F(x)}{d{x}^2}=-{\omega }^2}$

Integramos la primera ecuación diferencial

${\displaystyle \begin{array}{l}\frac{dG(t)}{dt}+\alpha {\omega }^{2}G(t)=0\\ G(t)=G(0)·\exp \left(-\alpha {\omega }^{2}t\right)\end{array}}$

Integramos la segunda ecuación diferencial

${\displaystyle \frac{d^{2}F(x)}{d{x}^2}+{\omega }^{2}F(x)=0}$

Es una ecuación diferencial similar a la de un Movimiento Armónico Simple, cuya solución es F(x)=Asin(ωx)+Bcos(ωx)

Solución general

• En el extremo izquierdo de la varilla x=0, u(0, t)=0, F(0)=0, por lo que B=0. F(x)=Asin(ωx)

• En el extremo derecho de la varilla x=L, la derivada F(x) debe cumplir que, Aωcos(ωL)=0, por lo que k=ωL=(2n+1)π/2, n=0,1,2,3...

La solución completa u(x,t) es la superposición

${\displaystyle u(x,t)={\displaystyle \sum _{n=0}^{\infty }{A}_n\sin \left(k_n\frac{x}{L}\right)\exp \left(-\alpha \frac{k_n^2}{L^2}t\right)}}$

Coeficientes A_n

Solamente, queda por determinar los coeficientes A_n, identificando la solución para t=0 con la condición inicial u(x,0)

${\displaystyle \begin{array}{l}u(x\mathrm{,0})={\displaystyle \sum _{n=0}^{\infty }{A}_n\sin \left(k_n\frac{x}{L}\right)}\hfill \\ T_0-T_a={\displaystyle \sum _{n=0}^{\infty }{A}_n\sin \left(k_n\frac{x}{L}\right)}\hfill \end{array}}$

Teniendo en cuenta la relación de ortogonalidad

${\displaystyle {\displaystyle \underset{0}{\overset{L}{\int }}\sin \left(k_n\frac{x}{L}\right)}\sin \left(k_m\frac{x}{L}\right)dx=0n\ne m}$

Obtenemos los coeficientes A_n

${\displaystyle A_n=\frac{{\displaystyle \underset{0}{\overset{L}{\int }}(T_0-T_a)\sin \left(\frac{k_{n}x}{L}\right)dx}}{{\displaystyle \underset{0}{\overset{L}{\int }}{\sin }^2\left(\frac{k_{n}x}{L}\right)dx}}=\frac{(T_0-T_a)\frac{L}{k_n}\left(1-\cos (k_n)\right)}{\frac{L}{2}\left(1-\frac{1}{2k_n}\sin (2k_n)\right)}}$

Teniendo en cuenta el valor de k_n=(2n+1)π/2

${\displaystyle A_n=4(T_0-T_a)\frac{1-\cos (k_n)}{2k_n-\sin (2k_n)}=4(T_0-T_a)\frac{1-\cos \left(\frac{2n+1}{2}\pi \right)}{\left(2n+1\right)\pi -\sin \left(\left(2n+1\right)\pi \right)}=\frac{4(T_0-T_a)}{\left(2n+1\right)\pi }}$

Solución completa

La solución completa es

${\displaystyle \begin{array}{l}u(x,t)={\displaystyle \sum _{n=0}^{\infty }{A}_n\sin \left(k_n\frac{x}{L}\right)\exp \left(-\alpha \frac{k_n^2}{L^2}t\right)}\\ T(x,t)=u(x,t)+T(x,\infty )=u(x,t)+T_a\\ T(x,t)=T_a+4(T_0-T_a){\displaystyle \sum _{n=0}^{\infty }\frac{1}{\left(2n+1\right)\pi }\sin \left(\frac{2n+1}{2}\pi \frac{x}{L}\right)\exp \left(-\frac{\alpha }{L^2}{\left(\frac{2n+1}{2}\pi \right)}^{2}t\right)}\end{array}}$

Cambiando la variable x por y

${\displaystyle T(y,t)=T_a+4(T_0-T_a){\displaystyle \sum _{n=0}^{\infty }\frac{1}{\left(2n+1\right)\pi }\sin \left(\frac{2n+1}{2}\pi \frac{y}{L}\right)\exp \left(-\frac{\alpha }{L^2}{\left(\frac{2n+1}{2}\pi \right)}^{2}t\right)}}$

Ejemplo

Sea una muestra de longitud L= 8 cm, la temperatura inicial es T₀=22°C, la temperatura del baño térmico y=0, es T_a=0°C. La difusividad térmica de la muestra es α=1.06·10^-7 m²/s

Representamos la evolución de la temperatura de la muestra con el tiempo t en minutos en las posiciones y=0.5, 1, 1.5, 2, 2.5 y 3 cm

function difusividad
    alfa=1.06e-7; %difusividad térmica
    L=8; %altura del recipiente en cm
    T0=22; %temperatura inicial de la muestra
    Ta=0; %temperatura del baño térmico, x=0
    hold on
    for yHaz=0.5:0.5:3 %altura del haz y
        fplot(@(t) temperatura(yHaz, t), [0,25],'displayName',num2str(yHaz))
    end
    hold off
    grid on
    xlabel('t(min)')
    ylabel('T')
    legend('-DynamicLegend','location','best')
    title('Evolución de las temperaturas')
    
    function T=temperatura(y,t)
        suma=0;
        for n=0:500
            suma=suma+sin((2*n+1)*pi*y/(2*L))*exp(-alfa*((2*n+1)*pi*100
/(2*L))^2*t*60)/((2*n+1)*pi);
        end
        T=suma*4*(T0-Ta);
    end
end

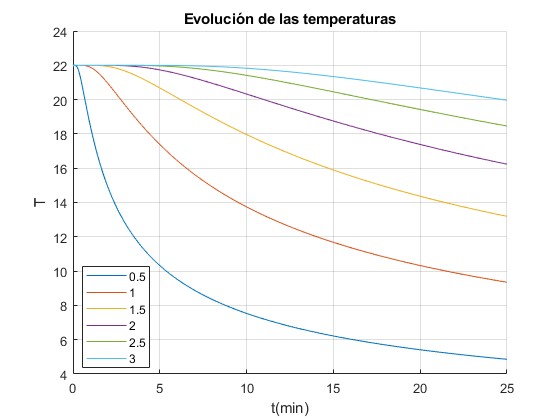
Cuando el tiempo es próximo a cero, hemos de sumar muchos términos a la serie, cuando el tiempo es grande bastan unos pocos términos

Al estar el extremo y=L aislado, los cambios significativos de temperatura se producen en las proximidades de y=0.

Gradiente térmico

Para calcular la desviación h del haz laser en la pantalla, precisamos la derivada dT/dy (gradiente térmico)

${\displaystyle \frac{dT(y,t)}{dy}=2\frac{T_0-T_a}{L}{\displaystyle \sum _{n=0}^{\infty }\cos \left(\frac{2n+1}{2}\pi \frac{y}{L}\right)\exp \left(-\frac{\alpha }{L^2}{\left(\frac{2n+1}{2}\pi \right)}^{2}t\right)}}$

Representamos la evolución del gradiente térmico dT(y,t)/dy de la muestra con el tiempo t en minutos en las mismas posiciones y=0.5, 1, 1.5, 2, 2.5 y 3 cm

function difusividad_4
    alfa=1.06e-7; %difusividad térmica
    L=8; %altura del recipiente en cm
    T0=22; %temperatura inicial de la muestra
    Ta=0; %temperatura del baño térmico, x=0
    hold on
    for yHaz=0.5:0.5:3 %altura del haz y
        fplot(@(t) gradiente(yHaz, t), [0,25],'displayName',num2str(yHaz))
    end
    hold off
    grid on
    ylim([-1,25])
    legend('-DynamicLegend','location','best')
    xlabel('t(min)')
    ylabel('dT(y,t)/dy')
    title('Gradiente térmico')

    function dT=gradiente(y,t)
        suma=0;
        for n=0:500
            suma=suma+cos((2*n+1)*pi*y/(2*L))*exp(-alfa*((2*n+1)*pi*
100/(2*L))^2*t*60);        
        end
        dT=suma*2*(T0-Ta)/L;
    end
end

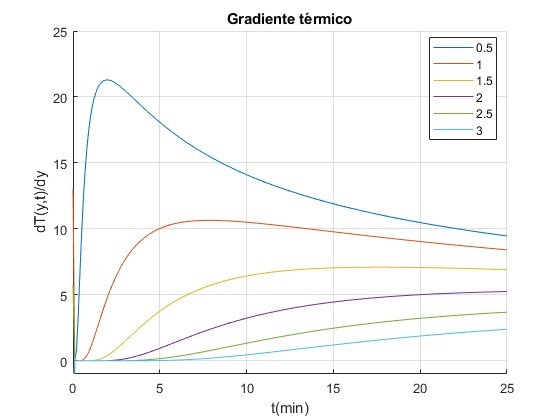
El gradiente térmico es acusado para las posiciones cercanas al baño térmico y=0, a 0°C,

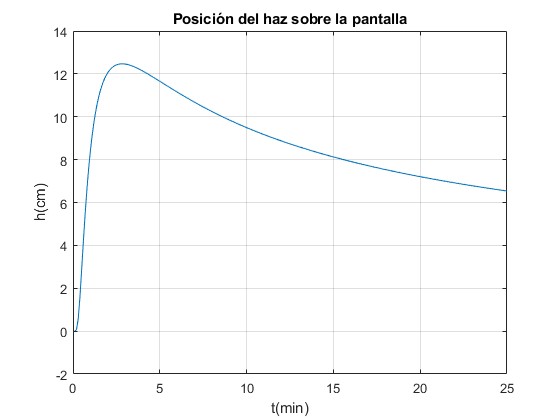
Posición del haz sobre la pantalla

Representamos la posición h del haz sobre la pantalla.

${\displaystyle h\approx -wd\frac{dn}{dy}=-wd\frac{dn}{dT}\frac{dT}{dy}}$

Los datos son

• Dimensiones de la muestra: altura L= 8 cm, espesor w=6 cm
• Temperatura inicial T₀=22°C, temperatura del baño térmico, y=0, T_a=0°C
• La difusividad térmica de la muestra es α=1.06·10^-7 m²/s
• El gradiente supuesto constante, dn/dT=1.2·10^-4 1/K
• La distancia de la muestra a la pantalla, d=9.76 m
• Altura del haz laser, y=0.9 cm

function difusividad_5
    alfa=1.06e-7; %difusividad térmica
    grad_n=1.2e-4; %gradiente dn/dT
    L=8; %altura del recipiente en cm
    espesor=6; %espesor de la muestra en cm
    d=9.76; %distancia a la pantalla
    T0=22; %temperatura inicial de la muestra
    Ta=0; %temperatura del baño térmico, x=0
    yHaz=0.6; %altura del haz

    fplot(@(t) fAltura(t), [0.1,25])
    grid on
    xlabel('t(min)')
    ylabel('h(cm)')
    title('Posición del haz sobre la pantalla')

    function h=fAltura(t)
        suma=0;
        for n=0:100
            suma=suma+cos((2*n+1)*pi*yHaz/(2*L))*exp(-alfa*((2*n+1)*pi*
100/(2*L))^2*t*60);
        end
        h=espesor*d*grad_n*suma*2*(T0-Ta)*100/L;
    end
end

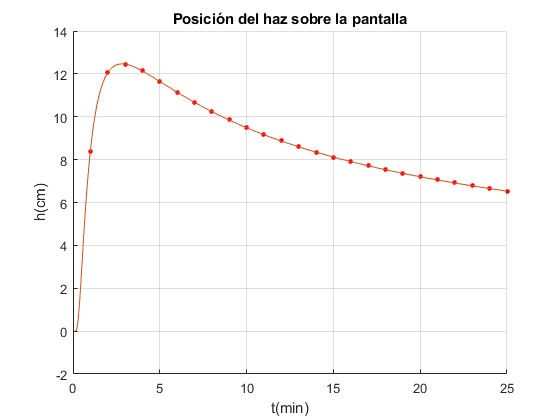
Determinación de la difusividad térmica

En la experiencia real, a partir de las medidas de las alturas h del haz en varios instantes de tiempo, se ajusta a dichos datos la función h(t) que depende de dos parámetros α y dn/dT. De este modo, se determina la difusividad térmica α=K/(ρc) de un material

Para ilustrar este procedimiento, generamos los datos de la experiencia simulada, tomando las alturas del haz a intervalos de un minuto y los guardamos en una tabla.

function difusividad_6
    alfa=1.06e-7; %difusividad térmica
    grad_n=1.2e-4; %gradiente dn/dT
    L=8; %altura del recipiente en cm
    espesor=6; %espesor de la muestra en cm
    d=9.76; %distancia a la pantalla
    T0=22; %temperatura inicial de la muestra
    Ta=0; %temperatura del baño térmico, x=0
    yHaz=0.6; %altura del haz
    t=1:25; %tiempo en minutos
    disp([t;fAltura(t)]) %tabla de datos 'experimentales'

    function h=fAltura(t)
        suma=0;
        for n=0:100
            suma=suma+cos((2*n+1)*pi*yHaz/(2*L))*exp(-alfa*((2*n+1)*
pi*100/(2*L))^2*t*60);
        end
        h=espesor*d*grad_n*suma*2*(T0-Ta)*100/L;
    end
end

En el código, la difusividad térmica α es a(1) y el gradiente dn/dT es a(2). Creamos el siguiente programa, para representar los datos experimentales mediante puntos de color rojo y la función h(t) que mejor ajusta a dichos datos experimentales

function difusividad_3
    t=1:25;
    y=[8.40, 12.05, 12.45, 12.14, 11.65, 11.15, 10.67, 10.24, 9.85, 
9.49, 9.16, 8.87, 8.60, 8.35, 8.12, 7.91, 7.71, 7.53, 7.36, 7.20, 
7.05, 6.91, 6.78, 6.65, 6.53];
    hold on
    plot(t,y,'ro','markersize',3,'markerfacecolor','r')
    L=8; %altura del recipiente en cm
    espesor=6; %espesor de la muestra en cm
    d=9.76; %distancia a la pantalla
    T0=22; %temperatura inicial de la muestra
    Ta=0; %temperatura del baño térmico, x=0
    yHaz=0.6; %altura del haz

    f=@(a,t) fAltura(a,t);      
    error=@(a) sum((y-f(a,t)).^2);
    a0=[1e-7,1e-4];  %valor inicial
    af=fminsearch(error,a0);
    disp(af)
    g=@(t) fAltura(af,t);
    fplot(g,[0.1,25])
    hold off
    grid on
    xlabel('t(min)')
    ylabel('h(cm)')
    title('Posición del haz sobre la pantalla')

    function h=fAltura(a, t)
        suma=0;
        for n=0:100
            suma=suma+cos((2*n+1)*pi*yHaz/(2*L))*exp(-a(1)*((2*n+1)*pi*100
/(2*L))^2*t*60);
        end
        h=espesor*d*a(2)*suma*2*(T0-Ta)*100/L;
    end
end

   1.0e-03 *
    0.0001    0.1200

El valor de la difusividad térmica, a(1) es α=1.0·10^-7 y el gradiente a(2), dn/dT=1.2·10^-4. Que son los valores aproximados de los parámetros que hemos empleado para generar los datos 'experimentales'

Actividades

Se introduce

• La muestra entre dos posibles, en el control titulado Muestra
• α=1.06·10^-7 m²/s, dn/dT=1.2·10^-4 1/K
• α=9.4·10^-7 m²/s, dn/dT=2.4·10^-4 1/K
• La altura y del haz, en el control titulado Altura haz

Se pulsa el botón titulado Nuevo

Se observa la posición del haz h en cm (punto de color amarillo), sobre la pantalla (franja vertical de color negro) en función del tiempo t en minutos

Se representa gráficamente h en función de t

Referencias

Jed Brody, Phillip Andreae, C. Andrew Robinson. A simple optical probe of transient heat conduction. Am. J. Phys. 78 (5), May 2010. pp. 529-531

Wen-Tang Lee, Fong-Feng Lin, Yu-You Lou. A novel method to measure the thermal diffusivity of transparent materials. Phys. Educ. 57 (2022) 055015