Supongamos una anillo de longitud 2L=2πr, siendo r el radio. La posición P de un punto del anillo es la longitud x=rθ del arco

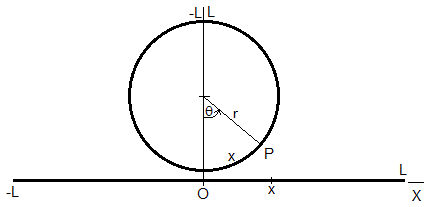
Para calcular la temperatura T(x,t) en un punto x del anillo y en un instante t, resolvemos la ecuación de la conducción del calor

${\displaystyle \frac{1}{\alpha }\frac{\partial T}{\partial t}=\frac{{\partial }^{2}T}{\partial x^2},-L\le x\le L,t>0}$

con las siguientes condiciones de contorno:

${\displaystyle \begin{array}{l}T\left(-L,t\right)=T\left(L,t\right)\\ {\frac{\partial T}{\partial x}|}_{-L}={\frac{\partial T}{\partial x}|}_L\end{array}}$

y la temperatura inicial T(x,0) dada por la función f(x)

${\displaystyle T\left(x\mathrm{,0}\right)=f(x),-L\le x\le L}$

Solución de la ecuación de la conducción del calor

Buscamos una solución de la forma T(x,t)=F(x)·G(t), variables separadas

${\displaystyle \begin{array}{l}\frac{1}{\alpha }F(x)\frac{\partial G}{\partial t}=G(t)\frac{{\partial }^{2}F}{\partial x^2}\\ \frac{1}{\alpha }\frac{1}{G(t)}\frac{dG}{dt}=\frac{1}{F(x)}\frac{d^{2}F}{d{x}^2}=-{\omega }^2\end{array}}$

A la izquierda, tenemos una función que depende solo de t, a la derecha, otra función que solamente depende de x, ambas son iguales a una constante que denominamos -ω²

Una ecuación diferencial en derivadas parciales se convierte en un sistema de dos ecuaciones diferenciales

${\displaystyle \{\begin{array}{l}\frac{dG}{dt}=-{\omega }^2\alpha G(t)\\ \frac{d^{2}F}{d{x}^2}=-{\omega }^{2}F(x)\end{array}}$

Integramos la primera ecuación diferencial

${\displaystyle \begin{array}{l}\frac{dG(t)}{dt}+\alpha {\omega }^{2}G(t)=0\\ G(t)=G(0)·\exp \left(-\alpha {\omega }^{2}t\right)\end{array}}$

Integramos la segunda ecuación diferencial

${\displaystyle \frac{d^{2}F(x)}{d{x}^2}+{\omega }^{2}F(x)=0}$

Cuando ω²≠0, es una ecuación diferencial similar a la de un Movimiento Armónico Simple, cuya solución es F(x)=Asin(ωx)+Bcos(ωx)

Cuando ω²=0, la solución es F(x)=A+Bx

Condiciones de contorno

• En el segundo caso, ω²=0

${\displaystyle \begin{array}{l}F\left(-L)=F(L\right)\\ A-BL=A+BL\\ {\frac{dF}{dx}|}_{-L}={\frac{dF}{dx}|}_L\\ A=A\end{array}}$

El resultado es B=0

• En el primer caso, ω²≠0

${\displaystyle \begin{array}{l}F\left(-L)=F(L\right)\\ A\sin \left(-\omega L\right)+B\cos \left(-\omega L\right)=A\sin \left(\omega L\right)+B\cos \left(\omega L\right)\\ {\frac{dF}{dx}|}_{-L}={\frac{dF}{dx}|}_L\\ \omega A\cos \left(-\omega L\right)-\omega B\sin \left(-\omega L\right)=\omega A\cos \left(\omega L\right)-\omega B\sin \left(\omega L\right)\end{array}}$

El sistema de dos ecuaciones se convierte en

${\displaystyle \{\begin{array}{l}2A\sin \left(\omega L\right)=0\\ 2B\sin \left(\omega L\right)=0\end{array}}$

Como A y B no pueden ser cero a la vez

${\displaystyle \omega L=n\pi ,n=\mathrm{1,2,3...}}$

Solución general

La solución completa T(x,t) es la superposición de los productos de las funciones F_n(x)·G_n(x) para n=0 y para cada ω_n=nπ/L, n=1,2,3...

${\displaystyle T\left(x,t\right)=a_0+\left\{{\displaystyle \sum _{n=1}^{\infty }{a}_n\cos \left(n\pi \frac{x}{L}\right)}+{\displaystyle \sum _{n=1}^{\infty }{b}_n\sin \left(n\pi \frac{x}{L}\right)}\right\}\exp \left(-\alpha \frac{n^2{\pi }^2}{L^2}x\right)}$

Solamente, queda por determinar los coeficientes a_n y b_n, identificando la solución para t=0 con la temperatura inicial T(x,0)=f(x)

${\displaystyle T\left(x\mathrm{,0}\right)=f(x)=a_0+{\displaystyle \sum _{n=1}^{\infty }{a}_n\cos \left(n\pi \frac{x}{L}\right)}+{\displaystyle \sum _{n=1}^{\infty }{b}_n\sin \left(n\pi \frac{x}{L}\right)},-L\le x\le L}$

Coeficiente a₀

Integramos entre -L y L

${\displaystyle {\displaystyle \underset{-L}{\overset{L}{\int }}f(x)dx}=a_0{\displaystyle \underset{-L}{\overset{L}{\int }}dx}+{\displaystyle \sum _{n=1}^{\infty }{a}_n{\displaystyle \underset{-L}{\overset{L}{\int }}\cos \left(n\pi \frac{x}{L}\right)dx}}+{\displaystyle \sum _{n=1}^{\infty }{b}_n{\displaystyle \underset{-L}{\overset{L}{\int }}\sin \left(n\pi \frac{x}{L}\right)dx}}}$

Resolvemos las integrales

• La primera integral es inmediata y vale 2L

• Segunda integral

${\displaystyle {{\displaystyle \underset{-L}{\overset{L}{\int }}\cos \left(m\pi \frac{x}{L}\right)dx=\frac{L}{m\pi }\sin \left(m\pi \frac{x}{L}\right)|}}_{-L}^L=0}$

• Tercera integral

${\displaystyle {{\displaystyle \underset{-L}{\overset{L}{\int }}\sin \left(m\pi \frac{x}{L}\right)dx=-\frac{L}{m\pi }\cos \left(m\pi \frac{x}{L}\right)|}}_{-L}^L=0}$

El coeficiente a₀ es

${\displaystyle a_0=\frac{1}{2L}{\displaystyle \underset{-L}{\overset{L}{\int }}f(x)dx}}$

Esta es la temperatura media inicial del anillo

Coeficientes a_n

Multiplicamos ambos miembros por cos(mπx/L) e integramos entre -L y L

${\displaystyle {\displaystyle \underset{-L}{\overset{L}{\int }}f(x)\cos \left(m\pi \frac{x}{L}\right)dx}=a_0{\displaystyle \underset{-L}{\overset{L}{\int }}\cos \left(m\pi \frac{x}{L}\right)dx}+{\displaystyle \sum _{n=1}^{\infty }{a}_n{\displaystyle \underset{-L}{\overset{L}{\int }}\cos \left(n\pi \frac{x}{L}\right)\cos \left(m\pi \frac{x}{L}\right)dx}}+{\displaystyle \sum _{n=1}^{\infty }{b}_n{\displaystyle \underset{-L}{\overset{L}{\int }}\sin \left(n\pi \frac{x}{L}\right)\cos \left(m\pi \frac{x}{L}\right)dx}}}$

Resolvemos las integrales

• Primera integral, ya la hemos resuelto

• Segunda integral

Hacemos un cambio de variable

${\displaystyle \begin{array}{l}{\displaystyle \underset{-L}{\overset{L}{\int }}\cos \left(n\pi \frac{x}{L}\right)}\cos \left(m\pi \frac{x}{L}\right)dx\\ z=\pi \frac{x}{L},dz=\pi \frac{dx}{L}\\ \frac{L}{\pi }{\displaystyle \underset{-\pi }{\overset{\pi }{\int }}\cos \left(nz\right)}\cos \left(mz\right)dz\end{array}}$

Integramos por partes

${\displaystyle \begin{array}{l}{\displaystyle \int \cos \left(nz\right)\cos \left(mz\right)dz,\{\begin{array}{l}u=\cos \left(nz\right),du=-n\sin \left(nz\right)dz\\ dv=\cos \left(mz\right)dz,v=\frac{1}{m}\sin \left(mz\right)\end{array}}\\ =\frac{1}{m}\cos \left(nz\right)\sin \left(mz\right)+\frac{n}{m}{\displaystyle \int \sin \left(nz\right)\sin \left(mz\right)dz}\\ {\displaystyle \int \sin \left(nz\right)\sin \left(mz\right)dz},\{\begin{array}{l}u=\sin \left(nz\right),du=n\cos \left(nz\right)dz\\ dv=\sin \left(mz\right)dz,v=-\frac{1}{m}\cos \left(mz\right)\end{array}\\ =-\frac{1}{m}\sin \left(nz\right)\cos \left(mz\right)+\frac{n}{m}{\displaystyle \int \cos \left(nz\right)\cos \left(mz\right)dz}\end{array}}$

El resultado de la integral es

${\displaystyle \begin{array}{l}{\displaystyle \int \cos \left(nz\right)\cos \left(mz\right)dz=}\frac{1}{m}\cos \left(nz\right)\sin \left(mz\right)+\frac{n}{m}\left\{-\frac{1}{m}\sin \left(nz\right)\cos \left(mz\right)+\frac{n}{m}{\displaystyle \int \cos \left(nz\right)\cos \left(mz\right)dz}\right\}\\ \left(1-\frac{n^2}{m^2}\right){\displaystyle \int \cos \left(nz\right)\cos \left(mz\right)dz}=\frac{1}{m}\cos \left(nz\right)\sin \left(mz\right)-\frac{n}{m^2}\sin \left(nz\right)\cos \left(mz\right)\\ \left(1-\frac{n^2}{m^2}\right){\displaystyle \underset{-\pi }{\overset{\pi }{\int }}\cos \left(nz\right)\cos \left(mz\right)dz=}{\frac{1}{m}\cos \left(nz\right)\sin \left(mz\right)-\frac{n}{m^2}\sin \left(nz\right)\cos \left(mz\right)|}_{-\pi }^{\pi }=0\end{array}}$

Cuando m=n

${\displaystyle \begin{array}{l}{\displaystyle \int {\cos }^2\left(nz\right)dz={\displaystyle \int \frac{1+\cos \left(2nz\right)}{2}}}dz=\frac{1}{2}\left(z+\frac{1}{2n}\sin \left(2nz\right)\right)\\ \frac{L}{\pi }{\displaystyle \underset{-\pi }{\overset{\pi }{\int }}{\cos }^2\left(nz\right)dz}=\frac{L}{\pi }\frac{1}{2}2\pi =L\end{array}}$

• Tercera integral

${\displaystyle \begin{array}{l}{\displaystyle \int \sin \left(nz\right)\cos \left(mz\right)dz,\{\begin{array}{l}u=\sin \left(nz\right),du=n\cos \left(nz\right)dz\\ dv=\cos \left(mz\right)dz,v=\frac{1}{m}\sin \left(mz\right)\end{array}}\\ =\frac{1}{m}\sin \left(nz\right)\sin \left(mz\right)+\frac{n}{m}{\displaystyle \int \cos \left(nz\right)\sin \left(mz\right)dz}\\ {\displaystyle \int \cos \left(nz\right)\sin \left(mz\right)dz},\{\begin{array}{l}u=\cos \left(nz\right),du=-n\sin \left(nz\right)dz\\ dv=\sin \left(mz\right)dz,v=-\frac{1}{m}\cos \left(mz\right)\end{array}\\ =-\frac{1}{m}\cos \left(nz\right)\cos \left(mz\right)-\frac{n}{m}{\displaystyle \int \sin \left(nz\right)\cos \left(mz\right)dz}\end{array}}$

El resultado de la integral es

${\displaystyle \begin{array}{l}{\displaystyle \int \sin \left(nz\right)\cos \left(mz\right)dz=}\frac{1}{m}\sin \left(nz\right)\sin \left(mz\right)+\frac{n}{m}\left\{-\frac{1}{m}\cos \left(nz\right)\cos \left(mz\right)-\frac{n}{m}{\displaystyle \int \sin \left(nz\right)\cos \left(mz\right)dz}\right\}\\ \left(1+\frac{n^2}{m^2}\right){\displaystyle \int \sin \left(nz\right)\cos \left(mz\right)dz}=\frac{1}{m}\sin \left(nz\right)\sin \left(mz\right)-\frac{n}{m^2}\cos \left(nz\right)\cos \left(mz\right)\\ \left(1+\frac{n^2}{m^2}\right){\displaystyle \underset{-\pi }{\overset{\pi }{\int }}\sin \left(nz\right)\cos \left(mz\right)dz=}{\frac{1}{m}\sin \left(nz\right)\sin \left(mz\right)-\frac{n}{m^2}\cos \left(nz\right)\cos \left(mz\right)|}_{-\pi }^{\pi }=0\end{array}}$

Cuando m=n

${\displaystyle \begin{array}{l}{\displaystyle \int \sin \left(nz\right)\cos \left(nz\right)dz=\frac{1}{2}{\displaystyle \int \sin \left(2nz\right)}}dz=-\frac{1}{4n}\cos \left(2nz\right)\\ \frac{L}{\pi }{\displaystyle \underset{-\pi }{\overset{\pi }{\int }}\sin \left(nz\right)\cos \left(nz\right)dz}=0\end{array}}$

El coeficiente a_n es

${\displaystyle a_n=\frac{1}{L}{\displaystyle \underset{-L}{\overset{L}{\int }}f(x)\cos \left(n\pi \frac{x}{L}\right)dx}}$

Coeficientes b_n

Multiplicamos ambos miembros por cos(mπx/L) e integramos entre -L y L

${\displaystyle {\displaystyle \underset{-L}{\overset{L}{\int }}f(x)\sin \left(m\pi \frac{x}{L}\right)dx}=a_0{\displaystyle \underset{-L}{\overset{L}{\int }}\sin \left(m\pi \frac{x}{L}\right)dx}+{\displaystyle \sum _{n=1}^{\infty }{a}_n{\displaystyle \underset{-L}{\overset{L}{\int }}\cos \left(n\pi \frac{x}{L}\right)\sin \left(m\pi \frac{x}{L}\right)dx}}+{\displaystyle \sum _{n=1}^{\infty }{b}_n{\displaystyle \underset{-L}{\overset{L}{\int }}\sin \left(n\pi \frac{x}{L}\right)\sin \left(m\pi \frac{x}{L}\right)dx}}}$

Siguiendo los mismos pasos, el resultado es

${\displaystyle b_n=\frac{1}{L}{\displaystyle \underset{-L}{\overset{L}{\int }}f(x)\sin \left(n\pi \frac{x}{L}\right)dx}}$

Solución completa

La temperatura en cualquier punto de la varilla x, en un instante t, se compone de la suma de un término contante (la temperatura media inicial del anillo) y de una serie rápidamente convergente que describe el estado transitorio.

${\displaystyle \begin{array}{l}T\left(x,t\right)=a_0+\left\{{\displaystyle \sum _{n=1}^{\infty }{a}_n\cos \left(n\pi \frac{x}{L}\right)}+{\displaystyle \sum _{n=1}^{\infty }{b}_n\sin \left(n\pi \frac{x}{L}\right)}\right\}\exp \left(-\alpha \frac{n^2{\pi }^2}{L^2}x\right)\\ a_0=\frac{1}{2L}{\displaystyle \underset{-L}{\overset{L}{\int }}f(x)dx}\\ a_n=\frac{1}{L}{\displaystyle \underset{-L}{\overset{L}{\int }}f(x)\cos \left(n\pi \frac{x}{L}\right)dx}\\ b_n=\frac{1}{L}{\displaystyle \underset{-L}{\overset{L}{\int }}f(x)\sin \left(n\pi \frac{x}{L}\right)dx}\end{array}}$

Ejemplo

El valor de α=K/(ρc) nos da una medida de la rapidez con la que el sistema alcanza el estado estacionario. Cuanto mayor sea α antes se alcanza el estado estacionario

Fuente: Koshkin N. I., Shirkévich M. G.. Manual de Física Elemental. Editorial Mir 1975. págs 36, 74-75, 85-86

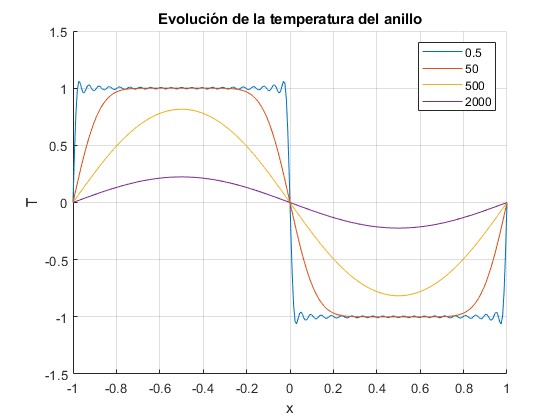
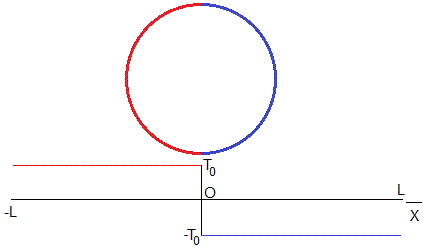
Un anillo hecho de aluminio se ha partido en dos mitades, la parte izquierda se ha calentado hasta alcanzar una temperatura T₀, la parte derecha se ha enfriado a -T₀. En el instante t=0, se unen las dos partes. Vamos a determinar la temperatura de cada punto del anillo en los instantes t=0.5, 50, 500, 2000 s

Coeficientes a_n y b_n

${\displaystyle \begin{array}{l}{a}_0=\frac{1}{2L}\left\{{\displaystyle \underset{-L}{\overset{0}{\int }}{T}_{0}dx}+{\displaystyle \underset{0}{\overset{L}{\int }}\left(-T_0\right)dx}\right\}=0\\ a_n=\frac{1}{L}\left\{{\displaystyle \underset{-L}{\overset{0}{\int }}{T}_0\cos \left(n\pi \frac{x}{L}\right)dx}+{\displaystyle \underset{0}{\overset{L}{\int }}\left(-T_0\right)\cos \left(n\pi \frac{x}{L}\right)dx}\right\}=0\\ b_n=\frac{1}{L}\left\{{\displaystyle \underset{-L}{\overset{0}{\int }}{T}_0\sin \left(n\pi \frac{x}{L}\right)dx}+{\displaystyle \underset{0}{\overset{L}{\int }}\left(-T_0\right)\sin \left(n\pi \frac{x}{L}\right)dx}\right\}=\frac{2T_0}{n\pi }\left(\cos \left(n\pi \right)-1\right)=\{\begin{array}{l}\mathrm{0,}n\text{par}\\ -\frac{4T_0}{n\pi },n\text{impar}\end{array}\end{array}}$

Véase también la página titulada Series de Fourier, el apartado 'Función impar'

La temperatura T(x,t) es

${\displaystyle T\left(x,t\right)=-\frac{4T_0}{\pi }{\displaystyle \sum _{n=\mathrm{1,3,5...}}^{\infty }\frac{1}{n}\sin \left(n\pi \frac{x}{L}\right)}\exp \left(-\alpha \frac{n^2{\pi }^2}{L^2}x\right)}$

function anilloT
    T0=1; %temperatura incial
    alfa=11352; %Coeficiente, 1/alfa del aluminio
    L=1; % longitud del anillo 2L
    
    hold on
    for t=[0.5, 50, 500, 2000]
        [x,T]=temperatura(t);
        plot(x,T,'displayName',num2str(t));
    end
    hold off 
    title('Evolución de la temperatura del anillo')
    xlabel('x')
    ylabel('T')
    legend('-DynamicLegend','location','northeast')
    grid on


    function [x,T]=temperatura(t)
       x=linspace(-L,L,300);
       T=zeros(length(x),1);
       cte=pi^2/(alfa*L^2);  
       j=1;
       for z=x
           for n=0:20
                T(j)=T(j)-4*T0*exp(-cte*(2*n+1)^2*t)*sin(pi*(2*n+1)*z/L)
/((2*n+1)*pi);
           end
           j=j+1;
       end
    end
end

Referencias

Heat conduction in a thin circular ring