El cilindro se calienta a una temperatura uniforme T₀ y se deja enfriar sumergiéndolo en un baño térmico a temperatura T_s.

En el estado estacionario, después de un tiempo t→∞, la temperatura final del cilindro será T(ρ,∞)=T_s, la temperatura del baño térmico.

La ecuación de la conducción del calor apropiada para resolver este problema es

${\displaystyle \frac{1}{\alpha }\frac{\partial T}{\partial t}=\frac{{\partial }^{2}T}{\partial {\rho }^2}+\frac{1}{\rho }\frac{\partial T}{\partial \rho }0\le \rho <a,t>0}$

ρ es la distancia radial desde el eje del cilindro.

Las condiciones de contorno son:

1. T(a,t)=T_s

2. ${\displaystyle -{\frac{\partial T(\rho ,t)}{\partial \rho }|}_{\rho =a}=h\left(T(a,t)-T_s\right)}$

La distribución inicial de temperaturas es T(ρ,0)=T₀

Solución de la ecuación de la conducción del calor (I)

Definimos la función u(ρ,t)=T(ρ,t)-T(ρ,∞), en términos de esta nueva función, la ecuación de la conducción del calor, las condición inicial en el instante t=0, y las condiciones de contorno en ρ=a se escriben

${\displaystyle \begin{array}{l}\frac{1}{\alpha }\frac{\partial u}{\partial t}=\frac{{\partial }^{2}u}{\partial {\rho }^2}+\frac{1}{\rho }\frac{\partial u}{\partial \rho }0<\rho <at>0\\ ·\text{contorno}\Rightarrow u(a,t)=0\\ ·\text{inicial}\Rightarrow u(x\mathrm{,0})=T_0-T_s\end{array}}$

Buscamos la solución mediante el procedimiento de separación de variables, de la forma u(ρ,t)=F(ρ)·G(t)

${\displaystyle \begin{array}{l}\frac{F}{\alpha }\frac{dG}{dt}=G\left(\frac{d^{2}F}{d^2\rho }+\frac{1}{\rho }\frac{dF}{d\rho }\right)\\ \frac{1}{F}\left(\frac{d^{2}F}{d^2\rho }+\frac{1}{\rho }\frac{dF}{d\rho }\right)=\frac{1}{\alpha }\frac{1}{G}\frac{dG}{dt}=-\frac{k^2}{a^2}\end{array}}$

Resolvemos la ecuación diferencial de la derecha

${\displaystyle \begin{array}{l}\frac{dG}{dt}+\frac{k^2\alpha }{a^2}G=0\\ G(t)=G(0)\exp \left(-\frac{k^2\alpha }{a^2}t\right)\end{array}}$

Resolvemos la ecuación diferencial de la izquierda

${\displaystyle \begin{array}{l}\frac{1}{F}\left(\frac{d^{2}F}{d^2\rho }+\frac{1}{\rho }\frac{dF}{d\rho }\right)=-\frac{k^2}{a^2}F\\ {\rho }^2\frac{d^{2}F}{d^2\rho }+\rho \frac{dF}{d\rho }+\frac{k^2}{a^2}{\rho }^{2}F=0\end{array}}$

Haciendo el cambio de variable y=F, x=kρ/a, obtenemos la ecuación de Bessel, cuya solución es

${\displaystyle \begin{array}{l}{x}^2\frac{d^{2}y}{d{x}^2}+x\frac{dy}{dx}+x^{2}y=0\\ y=A{J}_0(x)+B{Y}_0(x)\end{array}}$

Se descarta el segundo término por ser Y₀(x)=∞, cuando x tiende a cero

La solución es, F(ρ)=A·J₀(kρ/a).

Condiciones de contorno

La condición de contorno en ρ=a es T(a,t)=T_s, o bien, u(a,t)=F(a)·G(t)=0. Las raíces k_n, son los valores de k que cumplen la ecuación transcendente J₀(k)=0

La solución completa u(ρ,t) es la superposición

${\displaystyle u(\rho ,t)={\displaystyle \sum _{n=1}^{\infty }{A}_n{J}_0\left(k_n\frac{\rho }{a}\right)}\exp \left(-\frac{k_n^2\alpha }{a^2}t\right)}$

Condición inicial

Los coeficientes A_n se determinan a partir de la distribución inicial de temperaturas u(ρ,0)

${\displaystyle u(\rho \mathrm{,0})=T_0-T_s={\displaystyle \sum _{n=1}^{\infty }{A}_n{J}_0\left(k_n\frac{\rho }{a}\right)}}$

Despejamos A_n utilizando las relaciones de ortogonalidad de las funciones de Bessel, más abajo

${\displaystyle \begin{array}{l}(T_0-T_s){\displaystyle \underset{0}{\overset{a}{\int }}\rho J_0\left(k_m\frac{\rho }{a}\right)d\rho ={\displaystyle \sum _{n=1}^{\infty }{A}_n}}{\displaystyle \underset{0}{\overset{a}{\int }}\rho }{J}_0\left(k_m\frac{\rho }{a}\right)J_0\left(k_n\frac{\rho }{a}\right)d\rho \\ (T_0-T_s){\displaystyle \underset{0}{\overset{a}{\int }}\rho J_0\left(k_m\frac{\rho }{a}\right)d\rho =A_m{\displaystyle \underset{0}{\overset{a}{\int }}\rho }{J}_0^2\left(k_m\frac{\rho }{a}\right)d\rho }\end{array}}$

Haciendo el cambio de variable x=ρ/a y teniendo en cuenta los resultados de las integrales

${\displaystyle \begin{array}{l}(T_0-T_s){\displaystyle \underset{0}{\overset{1}{\int }}x{J}_0\left(k_{m}x\right)dx=A_m{\displaystyle \underset{0}{\overset{1}{\int }}x}{J}_0^2\left(k_{m}x\right)dx}\\ (T_0-T_s)\frac{J_1\left(k_m\right)}{k_m}=\frac{1}{2}{A}_m\left(J_0^2\left(k_m\right)+J_1^2\left(k_m\right)\right)\\ A_m=\frac{2(T_0-T_s)J_1\left(k_m\right)}{\left(J_0^2\left(k_m\right)+J_1^2\left(k_m\right)\right)k_m}\end{array}}$

>> syms x k;
>> int('x*besselj(0,k*x)^2',x,0,1)
ans= besselj(0, k)^2/2 + besselj(1, k)^2/2
>> int('x*besselj(0,k*x)',x,0,1)
ans =besselj(1, k)/k

Cambiando m por n y teniendo en cuenta que k_n son las raíces de la ecuación transcendente J₀(k)=0. Los coeficientes A_n valen

${\displaystyle A_n=\frac{2(T_0-T_s)}{k_n{J}_1\left(k_n\right)}}$

Solución completa

${\displaystyle \begin{array}{l}u(\rho ,t)=2(T_0-T_s){\displaystyle \sum _{n=1}^{\infty }\frac{1}{k_n{J}_1(k_n)}{J}_0\left(k_n\frac{\rho }{a}\right)}\exp \left(-\frac{k_n^2\alpha }{a^2}t\right)\\ T(\rho ,t)=u(\rho ,t)+T(\rho ,\infty )=\\ T_s+2(T_0-T_s){\displaystyle \sum _{n=1}^{\infty }\frac{1}{k_n{J}_1(k_n)}{J}_0\left(k_n\frac{\rho }{a}\right)}\exp \left(-\frac{k_n^2\alpha }{a^2}t\right)\end{array}}$

Ejemplo

Representamos gráficamente la función J₀(x), para estimar aproximadamente donde se encuentran las raíces de la ecuación transcendente J₀(x)=0.

>> f=@(x) besselj(0,x);
>> fplot(f,[0,100])
>> xlabel('x')
>> ylabel('J_0(x)')
>> title('Función J_0(x)')
>> grid on

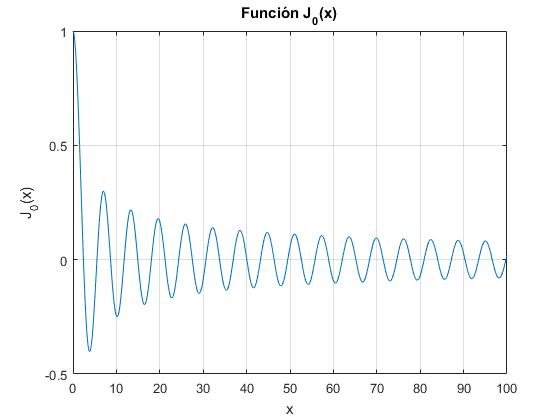
La función raices calcula las raíces múltiples de la función f(x) buscando los intervalos en los que dicha función cambia de signo y utilizando la función MATLAB fzero para encontrarlas

function r = raices(f, x)
    y=f(x);
    indices=find(y(1:end-1).*y(2:end)<0);
    r=zeros(1,length(indices));
    for k=1:length(indices)
        r(k)=fzero(f, [x(indices(k)), x(indices(k)+1)]);
    end
end

Definimos la función temperatura_5 para calcular la distribución de temperaturas a lo largo de de la dirección radial del cilindro en el instante t

function [r,T]=temperatura_5(T0,Ts,R,k,a2,t)
   r=linspace(0,R,100);
   if(t==0)
       T=T0*ones(1,length(r));
       return;
   end
      
   T=Ts*ones(1,length(r));
   for n=1:length(k)
        an=2*(T0-Ts)/(k(n)*besselj(1,k(n)));
        T=T+an*exp(-k(n)^2*t/(a2*R^2))*besselj(0,(k(n)*r/R));
   end
end

Creamos un script en el que establecemos la temperatura inicial T₀, la temperatura ambiente T_s, el radio a de un cilindro muy largo, el material del cual está hecho el cilindro, (parámetro α). El script calcula un número elevado de raíces k_n de la ecuación transcendente y representa la distribución radial de temperaturas del cilindro en varios instantes.

T0=100; %temperatura inicial
Ts=0; %temperatura ambiente
alfa=11352; %Coeficiente, 1/alfa del aluminio
R=1; % radio del cilindro

%raíces
x=linspace(0,100,100);
f=@(x) besselj(0,x);
k=raices(f,x);

hold on
axis([0 1 -5 100]);
for t=[10 500 1000 2000]
    [x,T]=temperatura_5(T0,Ts,R,k,alfa,t);
    plot(x,T,'displayName',num2str(t));
end
title('Evolución de la temperatura de un cilindro')
xlabel('r')
ylabel('Temperatura')
legend('-DynamicLegend','location','southwest')
grid on
hold off  

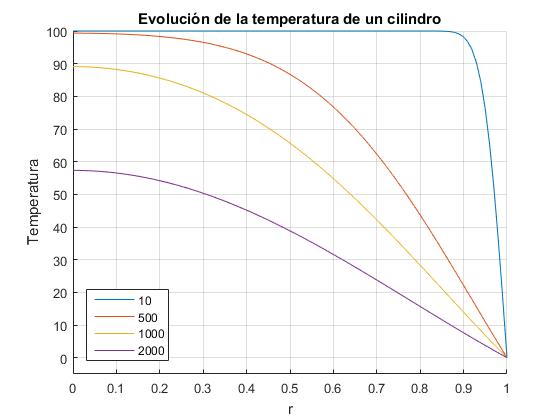
Una vez obtenidas las raíces k_n de la ecuación transcendente, J₀(k)=0, comprobamos las relaciones de ortogonalidad que hemos utilizado para calcular los coeficientes A_n

${\displaystyle {\displaystyle \underset{0}{\overset{1}{\int }}x{J}_0(k_{m}x)}{J}_0(k_{n}x)dx=0m\ne n}$

>> f=@(x) x.*(besselj(0,k(1)*x).*besselj(0,k(2)*x));
>> integral(f,0,1)  
ans =   8.9311e-18

Solución de la ecuación de la conducción del calor (II)

Definimos la función u(ρ,t)=T(ρ,t)-T(ρ,∞), en términos de esta nueva función, la ecuación de la conducción del calor, las condición inicial en el instante t=0, y las condiciones de contorno en ρ=a se escriben

${\displaystyle \begin{array}{l}\frac{1}{\alpha }\frac{\partial u}{\partial t}=\frac{{\partial }^{2}u}{\partial {\rho }^2}+\frac{1}{\rho }\frac{\partial u}{\partial \rho }0<\rho <at>0\\ ·\text{contorno}\Rightarrow {\frac{\partial u(\rho ,t)}{\partial \rho }|}_{\rho =a}+hu(a,t)=0\\ ·\text{inicial}\Rightarrow u(\rho \mathrm{,0})=T_0-T_s\end{array}}$

Buscamos la solución mediante el procedimiento de separación de variables, de la forma u(ρ,t)=F(ρ)·G(t)

${\displaystyle \begin{array}{l}\frac{F}{\alpha }\frac{dG}{dt}=G\left(\frac{d^{2}F}{d^2\rho }+\frac{1}{\rho }\frac{dF}{d\rho }\right)\\ \frac{1}{F}\left(\frac{d^{2}F}{d^2\rho }+\frac{1}{\rho }\frac{dF}{d\rho }\right)=\frac{1}{\alpha }\frac{1}{G}\frac{dG}{dt}=-\frac{k^2}{a^2}\end{array}}$

Resolvemos la ecuación diferencial de la derecha

${\displaystyle \begin{array}{l}\frac{dG}{dt}+\frac{k^2\alpha }{a^2}G=0\\ G(t)=G(0)\exp \left(-\frac{k^2\alpha }{a^2}t\right)\end{array}}$

Resolvemos la ecuación diferencial de la izquierda

${\displaystyle \begin{array}{l}\frac{1}{F}\left(\frac{d^{2}F}{d^2\rho }+\frac{1}{\rho }\frac{dF}{d\rho }\right)=-\frac{k^2}{a^2}F\\ {\rho }^2\frac{d^{2}F}{d^2\rho }+\rho \frac{dF}{d\rho }+\frac{k^2}{a^2}{\rho }^{2}F=0\end{array}}$

Haciendo el cambio de variable y=F, x=kρ/a, obtenemos la ecuación de Bessel, cuya solución es

${\displaystyle \begin{array}{l}{x}^2\frac{d^{2}y}{d{x}^2}+x\frac{dy}{dx}+x^{2}y=0\\ y=A{J}_0(x)+B{Y}_0(x)\end{array}}$

Se descarta el segundo término por ser Y₀(x)=∞, cuando x tiende a cero

La solución es, F(ρ)=A·J₀(kρ/a).

Condiciones de contorno

Dado que F(ρ)=J₀(kρ/a), la condición de contorno da lugar a una ecuación transcendente, cuyas raíces k_n son los valores de k que cumplen

${\displaystyle \begin{array}{l}{\frac{d{J}_0(k\rho /a)}{d\rho }|}_{\rho =a}+h{J}_0\left(k\right)=0\\ -\frac{k}{a}{J}_1(k)+h{J}_0\left(k\right)=0\end{array}}$

>> syms x k;
>> diff(besselj(0,k*x))
ans =-k*besselj(1, k*x)

La solución completa u(ρ,t) es la superposición

${\displaystyle u(\rho ,t)={\displaystyle \sum _{n=1}^{\infty }{A}_n{J}_0\left(k_n\frac{\rho }{a}\right)}\exp \left(-\frac{k_n^2\alpha }{a^2}t\right)}$

Condición inicial

Los coeficientes A_n se determinan a partir de la distribución inicial de temperaturas u(ρ,0)

${\displaystyle u(\rho \mathrm{,0})=T_0-T_s={\displaystyle \sum _{n=1}^{\infty }{A}_n{J}_0\left(k_n\frac{\rho }{a}\right)}}$

Despejamos A_n utilizando las relaciones de ortogonalidad de las funciones de Bessel, más abajo

${\displaystyle \begin{array}{l}(T_0-T_s){\displaystyle \underset{0}{\overset{a}{\int }}\rho J_0\left(k_m\frac{\rho }{a}\right)d\rho ={\displaystyle \sum _{n=1}^{\infty }{A}_n}}{\displaystyle \underset{0}{\overset{a}{\int }}\rho }{J}_0\left(k_m\frac{\rho }{a}\right)J_0\left(k_n\frac{\rho }{a}\right)d\rho \\ (T_0-T_s){\displaystyle \underset{0}{\overset{a}{\int }}\rho J_0\left(k_m\frac{\rho }{a}\right)d\rho =A_m{\displaystyle \underset{0}{\overset{a}{\int }}\rho }{J}_0^2\left(k_m\frac{\rho }{a}\right)d\rho }\end{array}}$

Haciendo el cambio de variable x=ρ/R y teniendo en cuenta los resultados de las integrales

${\displaystyle \begin{array}{l}(T_0-T_s){\displaystyle \underset{0}{\overset{1}{\int }}x{J}_0\left(k_{m}x\right)dx=A_m{\displaystyle \underset{0}{\overset{1}{\int }}x}{J}_0^2\left(k_{m}x\right)dx}\\ (T_0-T_s)\frac{J_1\left(k_m\right)}{k_m}=\frac{1}{2}{A}_m\left(J_0^2\left(k_m\right)+J_1^2\left(k_m\right)\right)\\ A_m=\frac{2(T_0-T_s)J_1\left(k_m\right)}{\left(J_0^2\left(k_m\right)+J_1^2\left(k_m\right)\right)k_m}\end{array}}$

>> syms x k;
>> int('x*besselj(0,k*x)^2',x,0,1)
ans= besselj(0, k)^2/2 + besselj(1, k)^2/2
>> int('x*besselj(0,k*x)',x,0,1)
ans =besselj(1, k)/k

Cambiando m por n y teniendo en cuenta que k_n son las raíces de la ecuación transcendente k·J₁(k)=ha·J₀(k). Los coeficientes A_n valen

${\displaystyle A_n=\frac{2(T_0-T_s)}{\left(k_n^2+h^2{a}^2\right)J_0\left(k_n\right)}}$

Solución completa

${\displaystyle \begin{array}{l}u(\rho ,t)=2(T_0-T_s){\displaystyle \sum _{n=1}^{\infty }\frac{1}{\left(k_n^2+h^2{a}^2\right)J_0\left(k_n\right)}{J}_0\left(k_n\frac{\rho }{a}\right)}\exp \left(-\frac{k_n^2\alpha }{a^2}t\right)\\ T(\rho ,t)=u(\rho ,t)+T(\rho ,\infty )=\\ T_s+2(T_0-T_s){\displaystyle \sum _{n=1}^{\infty }\frac{1}{\left(k_n^2+h^2{a}^2\right)J_0\left(k_n\right)}{J}_0\left(k_n\frac{\rho }{a}\right)}\exp \left(-\frac{k_n^2\alpha }{a^2}t\right)\end{array}}$

Ejemplo

Representamos gráficamente la función f(x)=x·J₁(x)-ha·J₀(x), para estimar aproximadamente donde se encuentran las raíces de la ecuación transcendente f(x)=0.

>> hR=10;
>> f=@(x) x*besselj(1,x)-hR*besselj(0,x);
>> fplot(f,[0,100])
>> xlabel('x')
>> ylabel('f(x)')
>> title('Función f(x)')
>> grid on

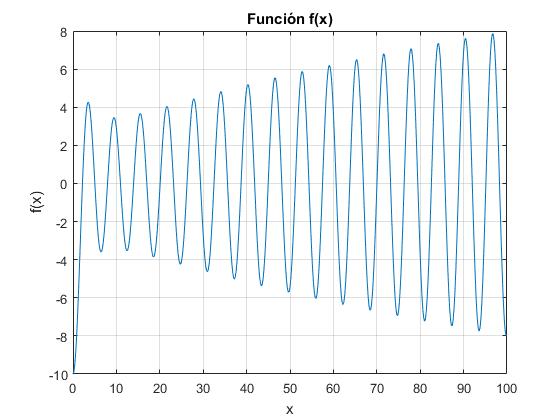
Definimos la función temperatura_7 para calcular la distribución de temperaturas a lo largo de de la dirección radial del cilindro en el instante t

function [r,T]=temperatura_7(T0,Ts,R,k,a2,t)
   r=linspace(0,R,100);
   if(t==0)
       T=T0*ones(1,length(r));
       return;
   end
      
   T=Ts*ones(1,length(r));
   for n=1:length(k)
        an=2*(T0-Ts)*besselj(1,k(n))/(k(n)*
(besselj(1,k(n))^2+besselj(0,k(n))^2));
        T=T+an*exp(-k(n)^2*t/(a2*R^2))*besselj(0,(k(n)*r/R));
   end
end

Creamos un script en el que establecemos la temperatura inicial T₀, la temperatura ambiente T_s, el radio a de un cilindro muy largo, el material del cual está hecho el cilindro, (parámetro α) y el parámetro ha, cuanto mayor sea su valor, mayor son las pérdidas por radiación de la superficie del cilindro. El script calcula un número elevado de raíces k_n de la ecuación transcendente y representa la distribución radial de temperaturas del cilindro en varios instantes.

T0=100; %temperatura inicial
Ts=0; %temperatura ambiente
alfa=11352; %Coeficiente, 1/alfa del aluminio
R=1; % radio del cilindro
hR=10; %pérdidas por radiación

%raíces
x=linspace(0,100,100);
f=@(x) x.*besselj(1,x)-hR*besselj(0,x);
k=raices(f,x);

hold on
axis([0 1 -5 100]);
for t=[50 500 1000 2000]
    [x,T]=temperatura_7(T0,Ts,R,k,alfa,t);
    plot(x,T,'displayName',num2str(t));
end
title('Evolución de la temperatura de un cilindro')
xlabel('r')
ylabel('Temperatura')
legend('-DynamicLegend','location','southwest')
grid on
hold off  

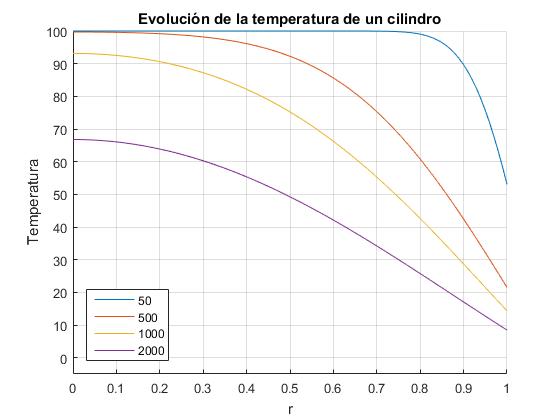
Conducción del calor en un disco

Consideremos ahora, el problema de la coducción del calor en un disco, un cilindro de pequeño espesor en relación con su radio, aislado en sus caras (bases)

La ecuación diferencial en derivadas parciales en coordenadas cilíndricas que describe la conducción del calor en un disco de radio a no depende de la coordenada z

${\displaystyle \frac{1}{\alpha }\frac{\partial T}{\partial t}=\frac{1}{\rho }\frac{\partial }{\partial \rho }\left(\rho \frac{\partial T}{\partial \rho }\right)+\frac{1}{{\rho }^2}\frac{{\partial }^{2}T}{\partial {\phi }^2}}$

• La condición inicial es, T(ρ, φ, 0)=100·ρ·cosφ

• La condición de contorno es, T(ρ, φ, t)=0, para t>0

Resolvemos la ecuación diferencial en derivadas parciales por el procedimiento de separación de variables. T(ρ, φ, t)=F(ρ, φ)·G(t)

${\displaystyle \begin{array}{l}F(\rho ,\phi )\frac{1}{\alpha }\frac{dG}{dt}=G(t)\left\{\frac{1}{\rho }\frac{\partial }{\partial \rho }\left(\rho \frac{\partial F}{\partial \rho }\right)+\frac{1}{{\rho }^2}\frac{{\partial }^{2}F}{\partial {\phi }^2}\right\}\\ \frac{1}{G(t)}\frac{1}{\alpha }\frac{dG}{dt}=\frac{1}{F(\rho ,\phi )}\left\{\frac{1}{\rho }\frac{\partial }{\partial \rho }\left(\rho \frac{\partial F}{\partial \rho }\right)+\frac{1}{{\rho }^2}\frac{{\partial }^{2}F}{\partial {\phi }^2}\right\}=-{\omega }^2\\ \{\begin{array}{l}\frac{dG}{dt}+\alpha {\omega }^{2}G=0\\ \frac{1}{\rho }\frac{\partial }{\partial \rho }\left(\rho \frac{\partial F}{\partial \rho }\right)+\frac{1}{{\rho }^2}\frac{{\partial }^{2}F}{\partial {\phi }^2}+{\omega }^{2}F=0\end{array}\end{array}}$

Integramos la primera ecuación diferencial

${\displaystyle G(t)=G(0)·\exp (-\alpha {\omega }^{2}t)}$

Resolvemos la segunda ecuación diferencial en derivadas parciales por el procedimiento de separación de variables F(ρ, φ)=R(ρ)·Φ(φ)

${\displaystyle \begin{array}{l}\frac{1}{\rho }\frac{\partial }{\partial \rho }\left(\rho \frac{\partial F}{\partial \rho }\right)+\frac{1}{{\rho }^2}\frac{{\partial }^{2}F}{\partial {\phi }^2}+{\omega }^{2}F=0\\ \Phi (\phi )\frac{1}{\rho }\frac{d}{d\rho }\left(\rho \frac{dR}{d\rho }\right)+R(\rho )\frac{1}{{\rho }^2}\frac{d^2\Phi }{d{\phi }^2}+{\omega }^{2}R(\rho )\Phi (\phi )=0\\ \frac{1}{R(\rho )}\rho \frac{d}{d\rho }\left(\rho \frac{dR}{d\rho }\right)+{\omega }^2{\rho }^2=-\frac{1}{\Phi (\phi )}\frac{d^2\Phi }{d{\phi }^2}=k^2\\ \{\begin{array}{l}{\rho }^2\frac{d^{2}R}{d{\rho }^2}+\rho \frac{dR}{d\rho }+\left({\omega }^2{\rho }^2-k^2\right)R=0\\ \frac{d^2\Phi }{d{\phi }^2}+k^2\Phi =0\end{array}\end{array}}$

Solución Φ(φ)

La solución de la segunda ecuación diferencial es sencilla

${\displaystyle \Phi (\phi )=\{\begin{array}{l}A\cos (k\phi )+B\sin (k\phi ),k\ne 0\\ a_0\phi +b_0,k=0\end{array}}$

Φ(φ)=Φ(φ+2π) tiene que ser una función periódica

• Para k≠0, implica

${\displaystyle \begin{array}{l}A\cos (k\phi )+B\sin (k\phi )=A\cos \left(k(\phi +2\pi )\right)+B\sin \left(k(\phi +2\pi )\right)\\ \sin \left(\alpha +k\phi \right)=\sin \left(\alpha +k(\phi +2\pi )\right),\tan \alpha =\frac{A}{B}\end{array}}$

Aplicando la fórmula de la diferencia de senos, sin(a+b)-sin(a-b)=2sinb·cosa

${\displaystyle \begin{array}{l}\{\begin{array}{l}a+b=\alpha +k(\phi +2\pi )\\ a-b=\alpha +k\phi \end{array}\{\begin{array}{l}a=\alpha +k(\phi +\pi )\\ b=k\pi \end{array}\\ \sin \left(k\pi \right)\cos \left(\alpha +k(\phi +\pi )\right)=\mathrm{0,}k=n,\text{entero}\end{array}}$

• Para k=0, implica que a₀=0

Solución R(ρ)

En la primera ecuación diferencial se hace el cambio x=ωρ, y(x)=R(ρ)

${\displaystyle x^2\frac{d^{2}y}{d{x}^2}+x\frac{dy}{dx}+\left(x^2-k^2\right)y=0}$

Se conoce como ecuación de Bessel. La solución de esta ecuación diferencial se escribe

${\displaystyle \begin{array}{l}y=A{J}_n(x)+B{Y}_n(x)\\ R(\rho )=A{J}_n(\omega \rho )+B{Y}_n(\omega \rho )\end{array}}$

Cuando ρ→0, Y_n(ωρ)→-∞, para que la solución esté acotada el coeficiente B tiene que ser nulo, B=0. La solución es R(ρ)=AJ_n(ωρ)

Condición de contorno

La condición de contorno, T(a, φ, t)=0 implica que R(a)=0, por lo que J_n(ωa)=0. En la página titulada Funciones de Bessel se proporciona una tabla de los primeros ceros de las funciones de Bessel J₀(x), J₁(x) y J₂(x).

Denominaremos los ceros de J_n(x)=0, r_n,m (m=1,2,3...)

La distribución de temperaturas en el disco de radio a en el instante t es la superposición

${\displaystyle T(\rho ,\phi ,t)={\displaystyle \sum _{n=\mathrm{1,}m=1}^{\infty }{J}_n\left(\frac{r_{n,m}}{a}\rho \right)}\left(A_{n,m}\cos (n\phi )+B_{n,m}\sin (n\phi )\right)\exp \left(-\alpha {\left(\frac{r_{n,m}}{a}\right)}^{2}t\right)}$

Distribución inicial de temperaturas

Los coeficientes A_n,m y B_n,m se calculan a partir de la distribución inicial de temperaturas

${\displaystyle T(\rho ,\phi \mathrm{,0})={\displaystyle \sum _{n,m}^{\infty }{J}_n\left(\frac{r_{n,m}}{a}\rho \right)}\left(A_{n,m}\cos (n\phi )+B_{n,m}\sin (n\phi )\right)}$

utilizando los resultados de las siguientes integrales

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{2\pi }{\int }}\sin \phi \cos (l\phi )d\phi =0}\\ {\displaystyle \underset{0}{\overset{2\pi }{\int }}\cos (n\phi )\cos (l\phi )d\phi =\{\begin{array}{l}\mathrm{0,}l\ne n\\ \pi ,l\ne n\end{array}}\\ {\displaystyle \underset{0}{\overset{2\pi }{\int }}\sin (n\phi )\cos (l\phi )d\phi =0}\\ {\displaystyle \underset{0}{\overset{2\pi }{\int }}\sin \phi \sin (l\phi )d\phi =\{\begin{array}{l}\mathrm{0,}l\ne 1\\ \pi ,l=1\end{array}}\\ {\displaystyle \underset{0}{\overset{2\pi }{\int }}\cos (n\phi )\sin (l\phi )d\phi =0}\\ {\displaystyle \underset{0}{\overset{2\pi }{\int }}\sin (n\phi )\sin (l\phi )d\phi =\{\begin{array}{l}\mathrm{0,}l\ne n\\ \pi ,l\ne n\end{array}}\end{array}}$

MATLAB nos ayuda a resolver algunas de las integrales, otras las podemos resolver rápidamente con lápiz y papel, utilizando las relaciones: cos(a-b)+cos(a+b)=2cosa·cosb, cos(a-b)-cos(a+b)=2sina·sinb

>> syms x m n;
>> assume(n,'integer')
>> assume(m,'integer')
>> int(sin(x)*cos(n*x),x,0,2*pi)
ans =0
>> z=int(sin(m*x)*cos(n*x),x,0,2*pi);
>> simplify(z)
ans =0
>> int(sin(x)*sin(n*x),x,0,2*pi)
ans =piecewise(n == 1, pi, n == -1, -pi, n ~= -1 & n ~= 1, 0)
>> int(cos(m*x)*sin(n*x),x,0,2*pi)
ans =0

${\displaystyle \begin{array}{l}100\rho \sin \phi ={\displaystyle \sum _{n=1}^{\infty }\left\{\cos (n\phi ){\displaystyle \sum _{m=1}^{\infty }{A}_{n,m}{J}_n\left(\frac{r_{n,m}}{a}\rho \right)+\sin (n\phi ){\displaystyle \sum _{m=1}^{\infty }{B}_{n,m}{J}_n\left(\frac{r_{n,m}}{a}\rho \right)}}\right\}}\\ 100\rho {\displaystyle \underset{0}{\overset{2\pi }{\int }}\sin \phi \cos (l\phi )d\phi ={\displaystyle \underset{0}{\overset{2\pi }{\int }}\left[{\displaystyle \sum _{n=1}^{\infty }\left\{\cos (n\phi ){\displaystyle \sum _{m=1}^{\infty }{A}_{n,m}{J}_n\left(\frac{r_{n,m}}{a}\rho \right)+\sin (n\phi ){\displaystyle \sum _{m=1}^{\infty }{B}_{n,m}{J}_n\left(\frac{r_{n,m}}{a}\rho \right)}}\right\}}\right]\cos (l\phi )d\phi }}\\ 100\rho {\displaystyle \underset{0}{\overset{2\pi }{\int }}\sin \phi \cos (l\phi )d\phi ={\displaystyle \sum _{n=1}^{\infty }\left\{\left({\displaystyle \sum _{m=1}^{\infty }{A}_{n,m}{J}_n\left(\frac{r_{n,m}}{a}\rho \right)}\right){\displaystyle \underset{0}{\overset{2\pi }{\int }}\cos (n\phi )\cos (l\phi )d\phi +\left({\displaystyle \sum _{m=1}^{\infty }{B}_{n,m}{J}_n\left(\frac{r_{n,m}}{a}\rho \right)}\right){\displaystyle \underset{0}{\overset{2\pi }{\int }}\sin (n\phi )\cos (l\phi )d\phi }}\right\}}}\\ 0=\left({\displaystyle \sum _{m=1}^{\infty }{A}_{l,m}{J}_l\left(\frac{r_{l,m}}{a}\rho \right)}\right)\pi \\ 100\rho {\displaystyle \underset{0}{\overset{2\pi }{\int }}\sin \phi \sin (l\phi )d\phi ={\displaystyle \underset{0}{\overset{2\pi }{\int }}\left[{\displaystyle \sum _{n=1}^{\infty }\left\{\cos (n\phi ){\displaystyle \sum _{m=1}^{\infty }{A}_{n,m}{J}_n\left(\frac{r_{n,m}}{a}\rho \right)+\sin (n\phi ){\displaystyle \sum _{m=1}^{\infty }{B}_{n,m}{J}_n\left(\frac{r_{n,m}}{a}\rho \right)}}\right\}}\right]\sin (l\phi )d\phi }}\\ 100\rho {\displaystyle \underset{0}{\overset{2\pi }{\int }}\sin \phi \sin (l\phi )d\phi ={\displaystyle \sum _{n=1}^{\infty }\left\{\left({\displaystyle \sum _{m=1}^{\infty }{A}_{n,m}{J}_n\left(\frac{r_{n,m}}{a}\rho \right)}\right){\displaystyle \underset{0}{\overset{2\pi }{\int }}\cos (n\phi )\sin (l\phi )d\phi +\left({\displaystyle \sum _{m=1}^{\infty }{B}_{n,m}{J}_n\left(\frac{r_{n,m}}{a}\rho \right)}\right){\displaystyle \underset{0}{\overset{2\pi }{\int }}\sin (n\phi )\sin (l\phi )d\phi }}\right\}}}\\ 100\rho {\displaystyle \underset{0}{\overset{2\pi }{\int }}\sin \phi \sin (l\phi )d\phi ={\displaystyle \sum _{n=1}^{\infty }\left\{\left({\displaystyle \sum _{m=1}^{\infty }{A}_{n,m}{J}_n\left(\frac{r_{n,m}}{a}\rho \right)}\right){\displaystyle \underset{0}{\overset{2\pi }{\int }}\cos (n\phi )\sin (l\phi )d\phi +\left({\displaystyle \sum _{m=1}^{\infty }{B}_{n,m}{J}_n\left(\frac{r_{n,m}}{a}\rho \right)}\right){\displaystyle \underset{0}{\overset{2\pi }{\int }}\sin (n\phi )\sin (l\phi )d\phi }}\right\}}}\\ \{\begin{array}{l}100\rho \pi ={\displaystyle \sum _{m=1}^{\infty }{B}_{\mathrm{1,}m}{J}_1\left(\frac{r_{\mathrm{1,}m}}{a}\rho \right)\pi ,l=1}\\ 0={\displaystyle \sum _{m=1}^{\infty }{B}_{l,m}{J}_1\left(\frac{r_{l,m}}{a}\rho \right)\pi ,l>1}\end{array}\end{array}}$

Utilizando las relaciones de ortogonalidad de las funciones de Bessel J_n(x) demostramos que los coeficientes A_n,m=0 y B_n,m=0 si n>1

${\displaystyle \begin{array}{l}0={\displaystyle \sum _{m=1}^{\infty }{A}_{l,m}{J}_l\left(\frac{r_{l,m}}{a}\rho \right)}\\ 0={\displaystyle \underset{0}{\overset{1}{\int }}x\left({\displaystyle \sum _{m=1}^{\infty }{A}_{l,m}{J}_l\left(r_{l,m}x\right)}\right)}{J}_l\left(r_{l,q}x\right)dx={\displaystyle \sum _{m=1}^{\infty }{A}_{l,m}{\displaystyle \underset{0}{\overset{1}{\int }}x{J}_l\left(r_{l,m}x\right)J_l\left(r_{l,q}x\right)dx}}=A_{l,q}·z\\ A_{l,q}=0\end{array}}$

La integral de la derecha es distinta de cero cuando m=q, el valor de la integral que denominamos z no tiene interés, depende del índice l de la función de Bessel J_l(x)

El mismo argumento se emplea para mostrar que los coeficientes B_l,m=0 con l>1. Los coeficientes B_1,m valen

${\displaystyle \begin{array}{l}100\rho ={\displaystyle \sum _{m=1}^{\infty }{B}_{\mathrm{1,}m}{J}_1\left(\frac{r_{\mathrm{1,}m}}{a}\rho \right)}\\ 100·a{\displaystyle \underset{0}{\overset{1}{\int }}{x}^2{J}_1\left(r_{\mathrm{1,}n}x\right)}dx={\displaystyle \underset{0}{\overset{1}{\int }}x\left({\displaystyle \sum _{m=1}^{\infty }{B}_{\mathrm{1,}m}{J}_1\left(r_{\mathrm{1,}m}x\right)}\right)}{J}_1\left(r_{\mathrm{1,}n}x\right)dx\\ 100·a{\displaystyle \underset{0}{\overset{1}{\int }}{x}^2{J}_1\left(r_{\mathrm{1,}n}x\right)}dx={\displaystyle \sum _{m=1}^{\infty }{B}_{\mathrm{1,}m}{\displaystyle \underset{0}{\overset{1}{\int }}x}{J}_1\left(r_{\mathrm{1,}m}x\right)J_1\left(r_{\mathrm{1,}n}x\right)dx}\\ 100·a\frac{J_2\left(r_{\mathrm{1,}m}\right)}{r_{\mathrm{1,}m}}=B_{\mathrm{1,}m}\frac{1}{2}{J}_2^2\left(r_{\mathrm{1,}m}\right)\\ B_{\mathrm{1,}m}=\frac{200·a}{r_{\mathrm{1,}m}}\frac{1}{J_2\left(r_{\mathrm{1,}m}\right)}\end{array}}$

Hemos utilizado la propiedad de las función de Bessel J_n(x)

${\displaystyle {\displaystyle \underset{0}{\overset{1}{\int }}{x}^{n+1}{J}_n(kx)dx=\frac{1}{k}}{J}_{n+1}(a)}$

La solución final de la ecuación diferencial en derivadas parciales que describe la conducción del calor en un disco es

${\displaystyle \begin{array}{l}T(\rho ,\phi ,t)={\displaystyle \sum _{m=1}^{\infty }{J}_1\left(\frac{r_{\mathrm{1,}m}}{a}\rho \right)}\left(B_{\mathrm{1,}m}\sin \phi \right)\exp \left(-\alpha {\left(\frac{r_{\mathrm{1,}m}}{a}\right)}^{2}t\right)\\ T(\rho ,\phi ,t)=200·a{\displaystyle \sum _{m=1}^{\infty }\frac{1}{r_{\mathrm{1,}m}}\frac{J_1\left(r_{\mathrm{1,}m}\frac{\rho }{a}\right)}{J_2\left(r_{\mathrm{1,}m}\right)}}\sin \phi ·\exp \left(-\alpha {\left(\frac{r_{\mathrm{1,}m}}{a}\right)}^{2}t\right)\end{array}}$

Donde r_1,m son los ceros de J₁(x)

Definimos la función disco_temperatura_5 para calcular la distribución de temperaturas en cada punto del disco y en el instante t

function T = disco_temperatura_5(r, phi, t, a, k, alfa)
    T=0;
    for n=1:length(k)
        T=T+besselj(1,r*k(n)/a).*sin(phi)*exp(-alfa*k(n)^2*t/a^2)
/(k(n)*besselj(2,k(n)));
    end
    T=T*200*a;
end

Creamos un script que calcula las primeras raíces de la función J₁(x). Establece el radio a=1 del disco y el material (aluminio) del que está hecho, o el valor de la constante α. Se fija el instante t y se representa la distribución de temperaturas en dicho instante

x=linspace(0,80,80);
raiz=raices(@(x) besselj(1,x),x); %raíces de J1(x)

t=100; %instante
alfa=1/11352; %aluminio
a=1; %radio del disco
r=0:0.1:a;
phi=0:pi/50:2*pi;
[r,phi]=meshgrid(r,phi);
T=disco_temperatura_5(r, phi, t, a, raiz, alfa); %T(r,phi)
x=r.*cos(phi);
y=r.*sin(phi);
surf(x,y,T)
xlabel('x/a')
ylabel('y/a')
zlabel('T(\rho,\phi)')
title('Temperatura del disco')
view(20,33)

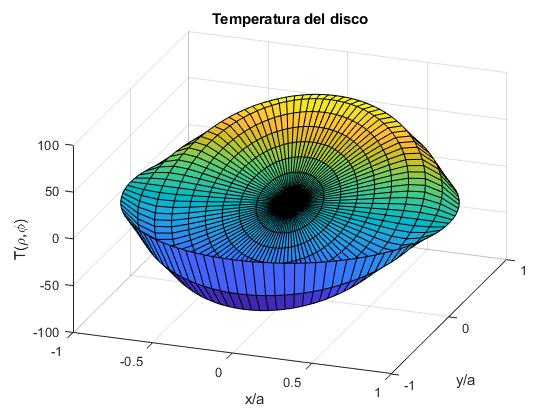
La temperatura del contorno del disco es cero, la temperatura de los puntos del disco va disminuyendo hasta que en el estado estacionario t→∞, la temperatura es cero en todos los puntos del disco

Referencias

Para el último apartado titulado 'Conducción del calor en un disco'

Physics 116C Home Page---Fall 2011, VI. Solutions to Homework Problem Sets and Exams. Problem 2