Equilibrio térmico (II)
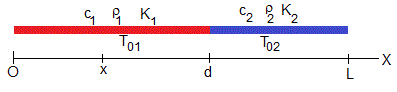
La varilla izquierda tiene una longitud d, está hecha de un material de calor específico c1, densidad ρ1 y conductividad térmica K1.
La varilla derecha tiene una longitud L-d, está hecha de un material de calor específico c2, densidad ρ2 y conductividad térmica K2.
Estudiaremos una situación en la que los extremos de las varillas se mantienen aislados.
Sus temperaturas iniciales son distintas T1(x,0)=T01 y T2(x, 0)=T02.
En un instante t, la distribución de temperaturas en la parte izquierda es T1(x, t) y en la parte derecha, T2(x, t). Soluciones de las ecuaciones diferencial en derivadas parciales
Con las condiciones iniciales y de controno especificadas. En la posición d de contacto de los dos tramos se ha de cumplir
La función T(x,t) es continua y el flujo de calor a través de la sección de la varilla en la posición de contacto d, a uno y otro lado, es el mismo
Una situación similar la encontramos en la propagación de ondas en una cuerda no homogénea
Estado estacionario
Consideremos dos cuerpos, el primero fabricado con un material de calor específico c1 y densidad ρ1 y el segundo, con un material de calor específico c2 y densidad ρ2
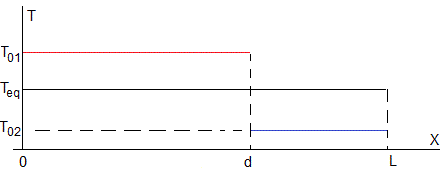
Inicialmente, cada cuerpo está a una temperatura T01 y T02, en recintos adiabáticos separados. En el instante t=0, se elimina la pared de separación y se ponen en contacto. Después de un tiempo, teóricamente infinito, los cuerpos adquieren una temperatura común de equilibrio Teq, ya que el calor cedido por el cuerpo caliente Q es absorbido por el cuerpo más frío (se supone que no hay pérdidas de calor).
En el estado estacionario, T1(x,∞)=Teq, T2(x,∞)=Teq
Supondremos que los dos cuerpos (varillas) tienen la misma sección S. La masa de cada varilla es proporcional a su longitud
Solución de la ecuación de la conducción del calor
Definimos las funciones: u1(x,t)=T1(x,t)-T1(x,∞) y u2(x,t)=T2(x,t)-T2(x,∞). En términos de estas nuevas funciones, las ecuaciones de la conducción del calor se esciben,
Condiciones iniciales
Condiciones de contorno, extremos aislados
Posición d de contacto
Variables separadas
Buscamos una solución de la forma u(x,t)=F(x)·G(t), variables separadas
Integramos la primera ecuación diferencial
Integramos la segunda ecuación diferencial
Las soluciones de la segunda, para cada una de las tramos de la varilla, son
La condición de contorno en el extremo izquierdo
La condición de contorno en el extremo derecho
En la posición d de contacto, se cumplirá que
Tenemos un sistema homogéneo de tres ecuaciones con tres incógnitas B1 ,A2 y B2. Despejamos A2 y B2 en función de B1
Las funciones F1(x) y F2(x) se expresan
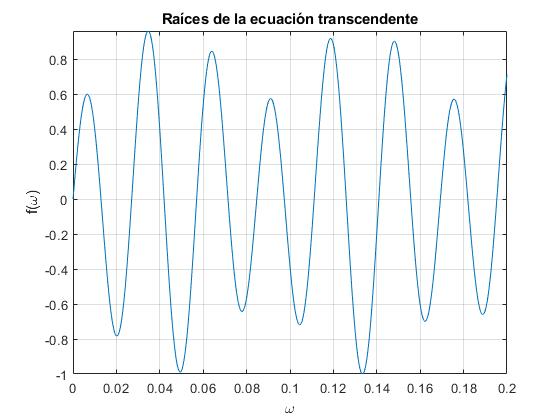
Además, obtenemos una ecuación transcendente (el determinante de los coeficientes del sistema homogéneo ha de ser nulo)
La primera raíz es ω0=0
Utilizamos la función
Ejemplo
Consideremos dos varillas que difieren en su conductividad térmica
- Varilla izquierda, hecha de aluminio, tiene las siguientes caraterísticas: densidad ρ1=2700, calor específico, c1=880, conductividad térmica, K1=209.3
- Varilla derecha, hecha de acero, tiene las siguientes caraterísticas: densidad ρ2=7800, calor específico, c2=460, conductividad térmica, K2=45. Todas las magnitudes en unidades S.I.
- La longitud de las dos varillas es L=1, la izquierdo es d=L/3 y la derecha L-d
- Las temperaturas iniciales de las varillas son T01=100 y T02=0
k1=209.3; %aluminio
c1=880;
r1=2700;
k2=45; %acero
c2=460;
r2=7800;
a1=sqrt(c1*r1/k1);
a2=sqrt(c2*r2/k2);
L=1; %longitud varilla
d=L/3; %posición contacto
%raíces wn
w=linspace(0,0.2,50);
f=@(w) sin(a1*w*d).*cos(a2*w*(L-d))+(k2*a2/(k1*a1))*sin(a2*w*(L-d)).*cos(a1*w*d);
raiz=raices(f,w);
fplot(f,[0,0.2])
xlabel('\omega')
ylabel('f(\omega)')
grid on
title('Raíces de la ecuación transcendente')
raiz =
0.0129 0.0270 0.0420 0.0570 0.0714 0.0847 0.0974 0.1111
0.1259 0.1409 0.1557 0.1693 0.1819 0.1953
La representación gráfica nos ayuda a establecer el paso de exploración de la función y el intervalo o el número de raíces que deseamos obtener. Es conveniente, comprobar que las raíces obtenidas numéricamente se corresponden con los ceros de la función f(ω)
Solución completa
La solución completa u(x,t) es la superposición de los productos de las funciones Fn(x)·Gn(x) para cada ωn
Donde ω0=0
De forma abreviada expresamos la superposición
Relación de ortogonalidad
Se puede demostar que
Evaluamos esta relación, utilizando procedimientos numéricos
k1=209.3; %aluminio c1=880; r1=2700; k2=45; %acero c2=460; r2=7800; a1=sqrt(c1*r1/k1); a2=sqrt(c2*r2/k2); L=1; %longitud varilla d=L/3; %posición contacto %raíces wn w=linspace(0,0.2,50); f=@(w) sin(a1*w*d).*cos(a2*w*(L-d))+(k2*a2/(k1*a1))*sin(a2*w*(L-d)).*cos(a1*w*d); raiz=raices(f,w); w1=raiz(3); w2=raiz(4); X1_1=@(x) cos(a1*w1*x); X1_2=@(x) cos(a1*w2*x); X2_1=@(x) cos(a1*w1*d)*cos(a2*w1*(L-x))/cos(a2*w1*(L-d)); X2_2=@(x) cos(a1*w2*d)*cos(a2*w2*(L-x))/cos(a2*w2*(L-d)); Z1=@(x) X1_1(x).*X1_2(x); Z2=@(x) X2_1(x).*X2_2(x); res=c1*r1*integral(Z1,0,d)+c2*r2*integral(Z2,d,L); disp(res)
7.0315e-08
Coeficientes Bn
Los coeficientes Bn se calculan a partir de las distribución inicial de temperatura u(x,0)
Multiplicamos la primera ecuación por X1m y la segunda por X2m e integramos entre 0 y d, la primera y entre d y L, la segunda
Sumamos
El primer coeficiente B0, correspondiente a ω0=0, merece un cálculo aparte. X10=1, X20=1
Introduciendo la expresión de la temperatura final de equilibrio, Teq. El resultado es B0=0
Los otros coeficientes Bn son
Utilizaremos procedimientos numéricos para calcular la expresión entre corchetes del segundo miembro de la igualdad.
Una vez calculados los coeficientes Bn, se ha completado la función u(x, t). Ahora queda la temperatura de la varilla, T(x, t)=u(x, t)+T(x, ∞)=u(x, t)+Teq
Dado que la exponencial disminuye rápidamente con el tiempo y por otra parte, los valores de las raíces ωn se hacen grandes, basta sumar unos pocos términos a la serie para obtener buenos resultados.
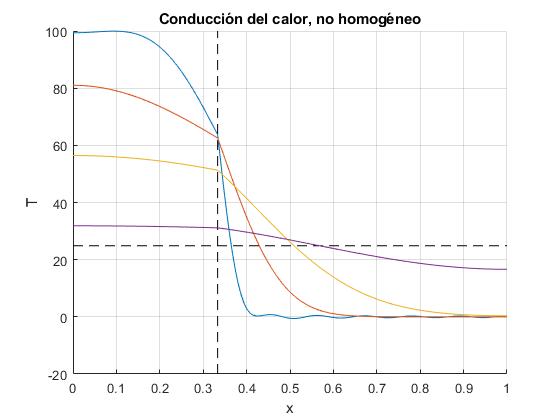
Completamos el programa para representar la distribución de temperaturas en los instantes t: 50, 500, 2000, 10000 s. La línea horizontal a trazos corresponden al estado estacionario. La parte derecha de la varilla, está hecha de acero y la parte izquierda, de aluminio de conductividad térmica K mucho mayor
k1=209.3; %aluminio
c1=880;
r1=2700;
k2=45; %acero
c2=460;
r2=7800;
a1=sqrt(c1*r1/k1);
a2=sqrt(c2*r2/k2);
T01=100; %temperaturas iniciales
T02=0;
L=1; %longitud varilla
d=L/3; %posición contacto
%estado estacionario, temperatura de equilibrio
Teq=(r1*d*c1*T01+r2*(L-d)*c2*T02)/(r1*d*c1+r2*(L-d)*c2);
%raíces wn
w=linspace(0,0.2,50);
f=@(w) sin(a1*w*d).*cos(a2*w*(L-d))+(k2*a2/(k1*a1))*sin(a2*w*(L-d)).*cos(a1*w*d);
raiz=raices(f,w);
%amplitudes An
A=zeros(1,length(raiz));
for n=1:length(raiz)
w=raiz(n);
X1=@(x) cos(a1*w*x);
X2=@(x) cos(a1*w*d)*cos(a2*w*(L-x))/cos(a2*w*(L-d));
Z1=@(x) X1(x).^2;
Z2=@(x) X2(x).^2;
den=integral(Z1,0,d)+(r2*c2/(r1*c1))*integral(Z2,d,L);
num=(T01-Teq)*sin(a1*w*d)/(a1*w)+(r2*c2/(r1*c1))*(T02-Teq)*
cos(a1*w*d)*sin(a2*w*(L-d))/(a2*w*cos(a2*w*(L-d)));
A(n)=num/den;
end
hold on
line([0,L],[Teq,Teq],'lineStyle','--','color','k')
line([d,d],[-20,100],'lineStyle','--','color','k')
x1=linspace(0,d,50);
x2=linspace(d,L,100);
for t=[50,500,2000, 10000]
u1=zeros(1,length(x1));
u2=zeros(1,length(x2));
for n=1:length(raiz)
w=raiz(n);
u1=u1+A(n)*cos(a1*w*x1)*exp(-w^2*t);
u2=u2+A(n)*cos(a1*w*d)*cos(a2*w*(L-x2))*exp(-w^2*t)/cos(a2*w*(L-d));
end
T=[u1+Teq,u2+Teq];
x=[x1,x2];
plot(x,T)
end
hold off
xlabel('x')
ylabel('T')
grid on
title('Conducción del calor, no homogéneo')