Condición de contorno

Una esfera de radio a recibe un flujo de calor y pierde calor debido a la radiación, la condición de contorno en su superficie se escribe

${\displaystyle {\frac{\partial T(r,\theta )}{\partial r}|}_{r=a}=-h(T(a,\theta )-T_s)+\frac{q}{K}}$

Donde T(a,θ) es la temperatura de la superficie de la esfera, T_s es la temperatura ambiente que la rodea y cuyo valor supondremos que es cero. Explicaremos el significado del término q

Una esfera de radio a se encuentra a una distancia r del centro del Sol. Si r es muy grande, las ondas electromagnéticas procedentes del Sol serán aproximadamente planas, los rayos procedentes del Sol que llegan a media esfera serán paralelos tal como se muestra en la figura.

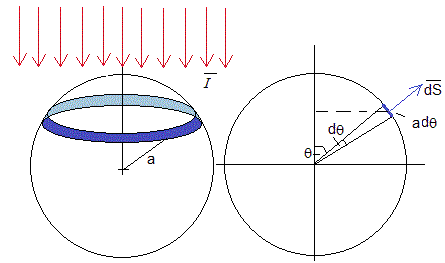
Denominamos $\overrightarrow{I}$ al vector que nos da la intensidad o energía emitida por el Sol en todas las frecuencias por unidad de tiempo y unidad de área. Lo pondremos, arbitrariamente, paralelo al eje Z. La dirección del vector superficie $\overrightarrow{dS}$ es radial.

El flujo de energía (energía por unidad de tiempo) que se recibe en la porción dS de la superficie de la esfera es el producto escalar $\overrightarrow{I}·\overrightarrow{dS}=I·dS\cos \theta$ .

La energía por unidad de área y unidad de tiempo que se recibe en la posición θ sobre la superficie de la esfera es q=Icosθ

La condición de contorno en la superficie de la esfera r=a, se escribe

${\displaystyle {\frac{\partial T(r,\theta )}{\partial r}|}_{r=a}=-hT(a,\theta )+f(\theta ),f(\theta )=\{\begin{array}{l}p\cos \theta ,0\le \theta <\frac{\pi }{2}\\ \mathrm{0,}\frac{\pi }{2}\le \theta <\pi \end{array}}$

Las posiciones θ≥π/2 representan la cara no iluminada de la esfera

Solución de la ecuación de Laplace

Solución de la ecuación de Laplace en coordenadas esféricas es

${\displaystyle T(r,\theta )={\displaystyle \sum _{n=0}^{\infty }\left(A_n{r}^n+\frac{B_n}{r^{n+1}}\right)}{P}_n(\cos \theta )}$

Vamos a calcular la temperatura en un punto interior de la esfera (r<a, θ). Dado que T(r, θ) no puede ser infinito cuando r→0, los coeficientes B_n=0 tienen anularse

Probamos la solución

${\displaystyle T(r,\theta )={\displaystyle \sum _{n=0}^{\infty }{A}_n{\left(\frac{r}{a}\right)}^n{P}_n(\cos \theta )}}$

Sustituimos en la condición de contorno

${\displaystyle {\displaystyle \sum _{n=0}^{\infty }{A}_n\frac{n}{a}{\left(\frac{a}{a}\right)}^{n-1}{P}_n(\cos \theta )}=-h\left({\displaystyle \sum _{n=0}^{\infty }{A}_n{\left(\frac{a}{a}\right)}^n{P}_n(\cos \theta )}\right)+f(\theta )}$

Desarrollo en serie en términos de los polinomios de Legendre

Expresamos una función f(x) como combinación lineal de los polinomios de Legendre

${\displaystyle \begin{array}{l}f(x)={\displaystyle \sum _{n=0}^{\infty }{c}_n{P}_n(x)}\\ c_n=\frac{2n+1}{2}{\displaystyle \underset{-1}{\overset{1}{\int }}f(x)P_n(x)dx},n=\mathrm{0,1,2...}\end{array}}$

Como f(θ) tiene valores no nulos en el intervalo (0, π/2), f(x)=p·x, con x=cosθ, está definida en el intervalo (0,1)

${\displaystyle c_n=\frac{2n+1}{2}{\displaystyle \underset{0}{\overset{\pi /2}{\int }}p\cos \theta ·P_n(\cos }\theta )\sin \theta ·d\theta =p\frac{2n+1}{2}{\displaystyle \underset{0}{\overset{1}{\int }}x{P}_n(x)dx},n=\mathrm{0,1,2...}}$

Calculamos los seis primeros coeficientes

>> syms x;
>> for n=0:5
int(legendreP(n,x)*x, 0,1)*(2*n+1)/2
end
ans =1/4
ans =1/2
ans =5/16
ans =0
ans =-3/32
ans =0

c₀=p/4, c₁=p/2, c₂=5p/6, c₃=0, c₄=-3p/32, c₅=0, ...

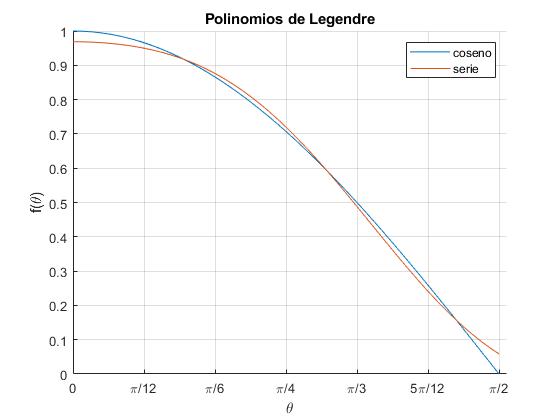
Representamos la función f(θ)=cosθ, en el intervalo (0, π/2) y los cinco primeros términos del desarrollo en serie, f(θ)≈c₀P₀(cosθ)+c₁P₁(cosθ)+c₂P₂(cosθ)+c₃P₃(cosθ)+c₄P₄(cosθ)

N=4; %número de términos
%coeficienets c_n
c=zeros(1,N+1);
for n=0:N %inicial
    c(n+1)=integral(@(x) legendreP(n,x).*x, 0,1)*(2*n+1)/2;
end
th=linspace(0,pi/2,100);
x=cos(th);
y=zeros(1,length(x));
for n=1:N+1 
    y=y+c(n)*legendreP(n-1,x);
end
hold on
fplot(@(x) cos(x),[0,pi/2])
plot(th,y)
set(gca,'XTick',0:pi/12:pi/2)
set(gca,'XTickLabel',{'0','\pi/12','\pi/6','\pi/4','\pi/3','5\pi/12','\pi/2'})
hold off
legend('coseno','serie')
xlabel('\theta')
ylabel('f(\theta)')
grid on
title('Polinomios de Legendre')

Temperatura de los puntos de la esfera T(r,θ) en el estado estacionario

Conocidos los coeficientes c_n, calculamos los coeficientes A_n

${\displaystyle \begin{array}{l}{\displaystyle \sum _{n=0}^{\infty }\frac{n}{a}{A}_n{P}_n(\cos \theta )}=-h\left({\displaystyle \sum _{n=0}^{\infty }{A}_n{P}_n(\cos \theta )}\right)+{\displaystyle \sum _{n=0}^{\infty }{c}_n{P}_n(\cos \theta )}\\ {\displaystyle \sum _{n=0}^{\infty }\left(\left(\frac{n}{a}+h\right)A_n-c_n\right)P_n(\cos \theta )}=0\\ A_n=\frac{a}{n+ha}{c}_n\end{array}}$

La temperatura de los puntos de la esfera T(r, θ) en el estado estacionario es

${\displaystyle \begin{array}{l}T(r,\theta )={\displaystyle \sum _{n=0}^{\infty }{A}_n{\left(\frac{r}{a}\right)}^n{P}_n(\cos \theta )}=\\ pa\left\{\frac{1}{4}+\frac{1}{2}\frac{1}{1+ha}\left(\frac{r}{a}\right)P_1(\cos \theta )+\frac{5}{16}\frac{1}{2+ha}{\left(\frac{r}{a}\right)}^2{P}_2(\cos \theta )-\frac{3}{32}\frac{5}{4+ha}{\left(\frac{r}{a}\right)}^4{P}_4(\cos \theta )+\mathrm{...}\right\}\end{array}}$

Con los datos

• Radio de la esfera, a=1
• Coeficiente de pérdidas por radiación, h=0.2
• Coeficiente de la intensidad de la radiación incidente en la superficie de la esfera, p=1

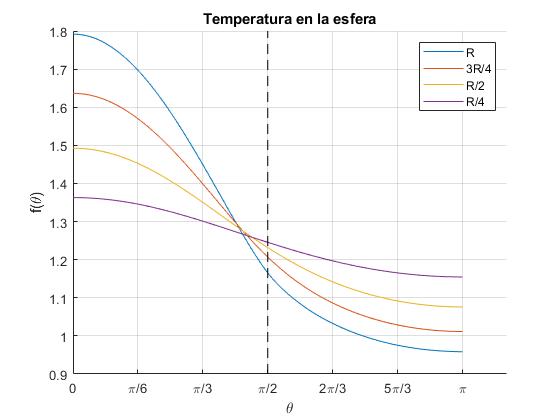
Representamos la temperatura T(r, θ), en el intervalo 0≤θ<π. Para los siguientes valores de r: r=a en la superficie de la esfera, para r=3a/4, r=a/2, r=a/4. Los puntos θ≥π/2 corresponden a la zona no iluminada, la temperatura de estos puntos es más fría en la superficie que en el interior

N=20; %número de términos
%coeficienets c_n
c=zeros(1,N+1);
for n=0:N %inicial
    c(n+1)=integral(@(x) legendreP(n,x).*x, 0,1)*(2*n+1)/2;
end
th=linspace(0,pi,100);
x=cos(th);
R=1;
h=0.2; %radiación
hold on
for r=[1,3/4,1/2,1/4]*R
    y=zeros(1,length(x));
    for n=1:N+1 
        y=y+(R/(n-1+h*R))*c(n)*(r/R)^(n-1)*legendreP(n-1,x);
    end
    plot(th,y)
end
line([pi/2,pi/2],[0.9,1.8],'lineStyle','--','color','k')
set(gca,'XTick',0:pi/6:pi)
set(gca,'XTickLabel',{'0','\pi/6','\pi/3','\pi/2', '2\pi/3', '5\pi/3','\pi'})
hold off
xlabel('\theta')
ylabel('f(\theta)')
legend('R','3R/4','R/2','R/4')
grid on
title('Temperatura en la esfera')

Si cambiamos el parámetro h=0.05, de modo que la esfera emita menos radiación al exterior, las temperaturas de los puntos de la esfera se incrementan, el perfil de las temperaturas es similar

Referencias

N. S. Kosholyakov, M. M. Smirnov, E. B. Gliner. Differential equations of Mathematical Physics. North-Holland Publishing Company (1964) pp. 371-373