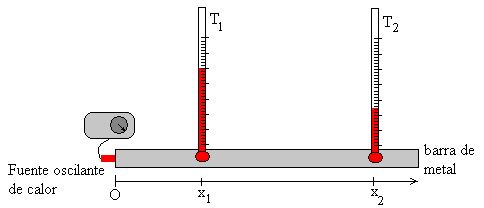
Se calienta el extremo de una barra de cobre de L=50 cm de longitud de forma periódica con un soldador conectado a un reloj. Después de comenzar el experimento, se deja pasar cierto tiempo hasta que se alcanza un estado de equilibrio dinámico en el que las temperaturas de cada punto de la barra oscilan alrededor de sus valores medios.

Se miden las temperaturas en dos puntos situados a una distancia x₁ y x₂ del origen de la barra. La relación entre las amplitudes de la oscilación térmica nos va proporcionar el valor del coeficiente de amortiguamiento y la diferencia de fase, la velocidad de propagación de las ondas térmicas en la barra. La relación entre estos dos parámetros nos proporciona el coeficiente α de la ecuación que describe la conducción térmica.

${\displaystyle \frac{\partial T}{\partial t}=\alpha \frac{{\partial }^{2}T}{\partial x^2}\text{,}\alpha =\frac{K}{\rho c}}$

donde α es un coeficiente que depende de la densidad ρ, calor específico c y conductividad térmica K del metal.

Calentamiento del extremo de la barra

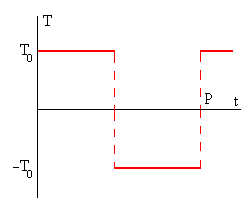
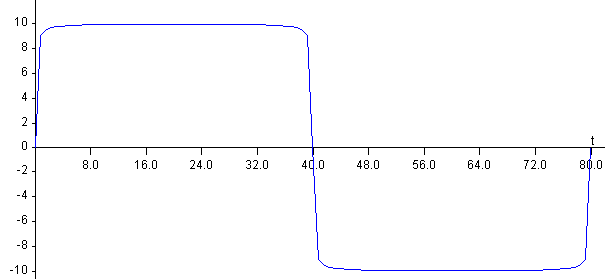
El calentamiento en el extremo de la barra x=0, se puede describir mediante un pulso periódico, de periodo P, en forma de escalón de altura 2·T₀, tal como se aprecia en la figura.

Esta función, se puede expresar en términos de un desarrollo en serie de Fourier.

Si f(t) es una función periódica de periodo P, se puede expresar en forma de desarrollo en serie de la forma.

${\displaystyle f(t)=\frac{a_0}{2}+{\displaystyle \sum _{n=1}^{\infty }\left(a_n\cos \left(n\frac{2\pi }{P}t\right)+b_n\text{sin}\left(n\frac{2\pi }{P}t\right)\right)}}$

donde

${\displaystyle \begin{array}{l}\frac{a_0}{2}=\frac{2}{P}{\displaystyle \underset{0}{\overset{P}{\int }}f(t)·dt}\\ a_n=\frac{2}{P}{\displaystyle \underset{0}{\overset{+P}{\int }}f(t)\cos \left(n\frac{2\pi }{P}t\right)·dt}n=\mathrm{1,}\text{ 2}\text{, 3}\mathrm{...}\\ b_n=\frac{2}{P}{\displaystyle \underset{0}{\overset{+P}{\int }}f(t)\sin \left(n\frac{2\pi }{P}t\right)·dt}n=\mathrm{1,}\text{ 2}\text{, 3}\mathrm{...}\end{array}}$

Para un escalón de potencial

f(t)=T₀ para 0≤t<P/2
f(t)=-T₀ para P/2≤t<P

Los coeficientes a_n y b_n de Fourier valen

${\displaystyle \begin{array}{l}{a}_0=\frac{2}{P}\left({\displaystyle \underset{0}{\overset{P/2}{\int }}{T}_{0}dt}+{\displaystyle \underset{P/2}{\overset{P}{\int }}(-T_0)dt}\right)=0\\ a_n=\frac{2}{P}\left({\displaystyle \underset{0}{\overset{P/2}{\int }}{T}_0\cos \left(n\frac{2\pi }{P}t\right)dt}+{\displaystyle \underset{P/2}{\overset{P}{\int }}(-T_0)\cos \left(n\frac{2\pi }{P}t\right)dt}\right)=0\\ b_n=\frac{2}{P}\left({\displaystyle \underset{0}{\overset{P/2}{\int }}{T}_0\sin \left(n\frac{2\pi }{P}t\right)dt}+{\displaystyle \underset{P/2}{\overset{P}{\int }}(-T_0)\sin \left(n\frac{2\pi }{P}t\right)dt}\right)=\{\begin{array}{l}\frac{4T_0}{n\pi }n=\mathrm{1,3,5..}\\ 0n=\mathrm{2,4,6...}\end{array}\end{array}}$

>> syms P n t;
>> an=(int(cos(2*n*pi*t/P),t,0,P/2)-int(cos(2*n*pi*t/P),t,P/2,P))*2/P;
>> subs(an,n,sym('[1 2 3 4 5]'))
ans =[ 0, 0, 0, 0, 0]
>> bn=(int(sin(2*n*pi*t/P),t,0,P/2)-int(sin(2*n*pi*t/P),t,P/2,P))*2/P;
>> subs(bn,n,sym('[1 2 3 4 5]'))
ans =[ 4/pi, 0, 4/(3*pi), 0, 4/(5*pi)]

El desarrollo en serie de la función escalón es

${\displaystyle f(t)={\displaystyle \sum _{n=\mathrm{1,3,5...}}^{\infty }\frac{4T_0}{n·\pi }\sin \left(n\frac{2\pi }{P}t\right)}}$

En la figura, se representa el calentamiento del extremo de la barra x=0, descrito por una función escalón de periodo P=80 s y cuya amplitud es de T₀=10º C.

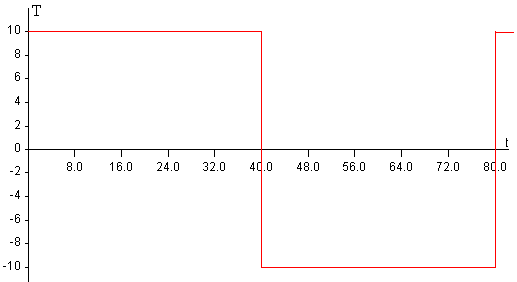
En la figura, se muestra la aproximación a la función escalón tomando los cinco primeros términos n=1, 3, 5, 7 y 9 del desarrollo en serie

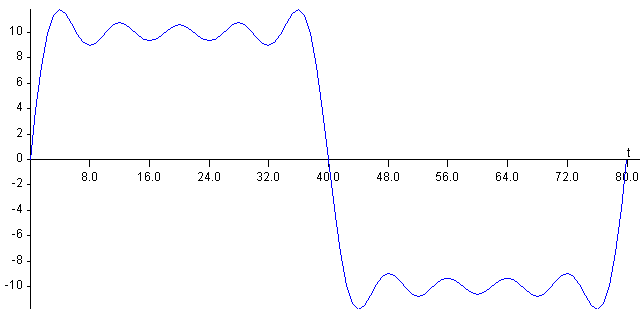
En esta otra figura, la aproximación a la función periódica tomando los 50 primeros términos cuyos índices n son los números impares que van desde n=1 a 99.

Propagación de la onda térmica

La distribución de temperaturas en la barra después de un tiempo de haber comenzado el experimento, cuando el sistema haya olvidado las condiciones iniciales, está dada por una serie, cada uno de cuyos términos corresponde a una onda armónica de frecuencia angular ω_n, número de onda k_n y velocidad de propagación v_n=ω_n/k_n.

${\displaystyle T(x,t)={\displaystyle \sum _{n=1}^{\infty }{A}_n(x)\sin ({\omega }_{n}t-k_{n}x)}}$

Introduciendo esta solución en la ecuación que describe la conducción térmica

${\displaystyle \frac{\partial T}{\partial t}=\alpha \frac{{\partial }^{2}T}{\partial x^2}\text{,}\alpha =\frac{K}{\rho c}}$

se obtiene

${\displaystyle {\displaystyle \sum _{n=1}^{\infty }\left(\frac{d^2{A}_n}{d{x}^2}-k_n^2{A}_n\right)}\sin ({\omega }_{n}t-k_{n}t)-{\displaystyle \sum _{n=1}^{\infty }\left(2\frac{d{A}_n}{dx}{k}_n+\frac{{\omega }_n}{\alpha }{A}_n\right)}\text{cos}({\omega }_{n}t-k_{n}t)=0}$

La igualdad a cero, conduce al sistema de dos ecuaciones diferenciales

${\displaystyle \begin{array}{l}2\frac{d{A}_n}{dx}{k}_n+\frac{{\omega }_n}{\alpha }{A}_n=0\\ \frac{d^2{A}_n}{d{x}^2}-k_n^2{A}_n=0\end{array}}$

Con la condición inicial en el extremo x=0 de la barra

${\displaystyle T(\mathrm{0,}t)={\displaystyle \sum _{n=\mathrm{1,3,5...}}^{\infty }\frac{4T_0}{n·\pi }\sin \left(n\frac{2\pi }{P}t\right)}={\displaystyle \sum _{n=\mathrm{1,3,5...}}^{\infty }\frac{4T_0}{n·\pi }\sin \left({\omega }_{n}t\right)}}$

Integramos la primera ecuación diferencial

${\displaystyle \frac{d{A}_n}{A_n}=-\frac{{\omega }_n}{2\alpha k_n}dx}$

con la condición inicial de que en x=0, A_n(0)=4·T₀/(n·π) para n=1,3,5... y A_n(0)=0 para n=2,4,6.... La solución es

${\displaystyle A_n(x)=\frac{4T_0}{n·\pi }\exp \left(-\frac{{\omega }_n}{2\alpha k_n}x\right)}$

Introduciendo A_n(x) en la segunda ecuación diferencial

${\displaystyle {\left(-\frac{{\omega }_n}{2\alpha k_n}\right)}^2{A}_n-k_n^2{A}_n=0\text{,}{k}_n=\sqrt{\frac{{\omega }_n}{2\alpha }}}$

La amplitud A_n(x) decrece exponencialmente con la distancia x a la fuente de calor de la forma

${\displaystyle A_n(x)=\frac{4T_0}{n·\pi }\exp \left(-k_{n}x\right)}$

La distribución de temperaturas para cada punto x de la barra en función del tiempo t es

${\displaystyle T(x,t)={\displaystyle \sum _{n=\mathrm{1,3,5...}}^{\infty }\frac{4T_0}{n·\pi }}\exp (-k_{n}x)·\sin \left({\omega }_{n}t-k_{n}x\right)\text{,}{\omega }_n=n\frac{2\pi }{P}\text{,}{k}_n=\sqrt{\frac{{\omega }_n}{2\alpha }}}$

La amplitud A_n(x) decrece rápidamente con x y también con n.  Los armónicos altos desaparecen, quedando lejos de la fuente tan solo el primer armónico n=1. La distribución de temperaturas para esos puntos se puede describir mediante la ecuación

${\displaystyle T(x,t)\approx \frac{\text{4}{T}_0}{\pi }\text{exp(-}k·x\text{)·sin}(\omega t-kx)\text{,}k=\sqrt{\frac{\omega }{2\alpha }}\text{,}\omega =\frac{2\pi }{P}}$

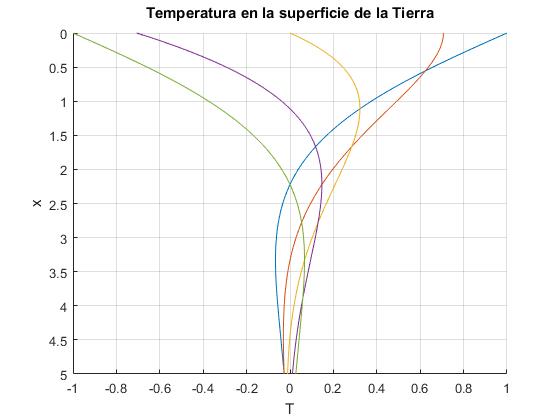
Esta expresión explica la variación de la temperatura con la profundidad bajo el suelo debido al calentamiento en verano y enfriamiento en invierno de la superficie terreste con un periodo de un año. Localmente la Tierra es plana y considaremos el eje X perpendicular a la superficie terrestre que se toma como origen y apuntando hacia abajo.

hold on
for t=(0:1/4:1)*pi
    f=@(x) exp(-sqrt(1/2)*x)*cos(t-sqrt(1/2)*x);
    fplot(f,[0,5])
end
hold off
xlabel('x')
ylabel('T')
title('Temperatura en la superficie de la Tierra')
grid on
view(90, -90)
set(gca, 'xdir', 'reverse');

En el script hemos girado los ejes de modo que la profundidad x aparece en el eje vertical. La amplitud de la oscilación térmica decrece exponencialmente con la profundidad x y con una diferencia de fase respecto de la superficie

La velocidad de propagación de las ondas térmicas es

${\displaystyle v=\frac{\omega }{k}=\sqrt{2\alpha \omega }}$

Cuando la velocidad de propagación v depende de la frecuencia ω, el medio se dice que es dispersivo.

El cociente v/(2k)=α que es un parámetro característico de cada metal en el proceso de conducción térmica.

Medida del coeficiente k de amortiguamiento de la amplitud

Como hemos demostrado, la amplitud de la onda armónica decrece exponencialmente con la distancia x a la fuente de calor situada en el extremo de la barra.

${\displaystyle A(x)=\frac{4T_0}{\pi }\exp (-kx)}$

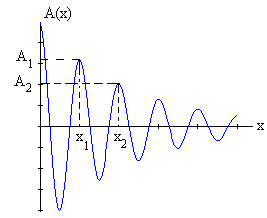
Colocamos dos termómetros a las distancias x₁ y x₂ lejos de la fuente de calor, para que la aproximación anterior sea válida.

Medimos la amplitud A₁ de la oscilación de la temperatura en la posición x₁

Medimos la amplitud A₂ de la oscilación de la temperatura en la posición x₂

${\displaystyle \frac{A_2}{A_1}=\exp \left(-k(x_2-x_1)\right)\text{,}k=\frac{1}{\Delta x}\ln \frac{A_1}{A_2}}$

Medida de la velocidad de propagación

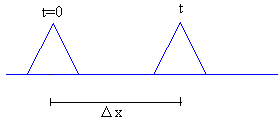
Cuando se propaga un Movimiento Ondulatorio, la perturbación, un pico, un valle, se desplaza una longitud Δx en un tiempo Δt. Si el máximo de temperatura  en el punto x₁ se produce en el instante t₁ y el máximo de temperatura en el punto x₂ se produce en el instante t₂. La velocidad de propagación v de las ondas térmicas, se obtiene mediante el cociente

${\displaystyle v=\frac{x_2-x_1}{t_2-t_1}=\frac{\Delta x}{\Delta t}}$

Tres velocidades caracterizan otros tantos procesos en un metal:

• La velocidad del sonido, que depende del módulo de Young y de la densidad del material, del orden de 3000 m/s para el cobre.

• La velocidad de los electrones del conducción del orden de 4·10^-7 m/s

• La velocidad de propagación de las ondas térmicas, del orden de 3·10^-3 m/s

Ejemplo

Creamos la función f_onda, que admite como parámetros: la amplitud de proceso de calentamiento-enfriamiento del extremo de la barra es T₀, el periodo P, el parámetro 1/α, la posición x a lo largo de la barra y el tiempo t en el que queremos calcular la distribución de temperaturas a lo largo de la barra. Devuelve la temperatura T de un punto x de la barra en el instante un instante t.

function T=f_onda(T0,P,a2,x,t)
   T=0;
   for n=1:2:19 %diez términos del desarrollo en serie
       w=n*2*pi/P;
       k=sqrt(w*a2/2);
       T=T+4*T0*exp(-k*x).*sin(w*t-k*x)/(n*pi);
   end
end

Creamos un script, que establece

• El metal de la barra
• La amplitud de proceso de calentamiento-enfriamiento del extremo de la barra es T₀=15º
• El periodo es P=80 s

Representamos la temperatura de la barra en función del tiempo durante un periodo. Para hacer la figura animada se ha empleado el siguiente código

T0=15; %La amplitud de calentamiento-enfriamiento del extremo de la barra
P=80; %periodo
a2=8909; %Coeficiente, 1/alfa del cobre

x=0:0.001:0.35;
fichero = 'onda_calor.gif';
for t=0:5:P
    T=f_onda(T0,P,a2,x,t);
    plot(x,T,'r')
    title('Ondas térmicas')
    xlabel('x (m)')
    ylabel('Temperatura')
    axis([0,0.35,-T0,T0])
    grid on
    
    frame=getframe;
    im = frame2im(frame);
    [imind,cm] = rgb2ind(im,256);
    if t==0
        imwrite(imind,cm,fichero,'gif','DelayTime',0,'loopcount',inf);
    else
        imwrite(imind,cm,fichero,'gif','DelayTime',0,'writemode','append');
    end
end

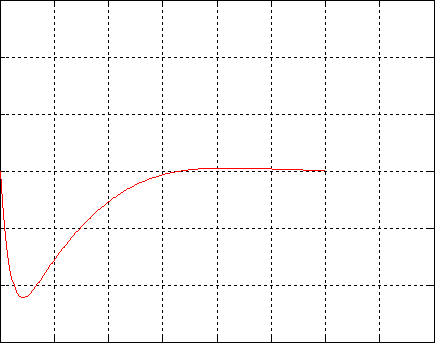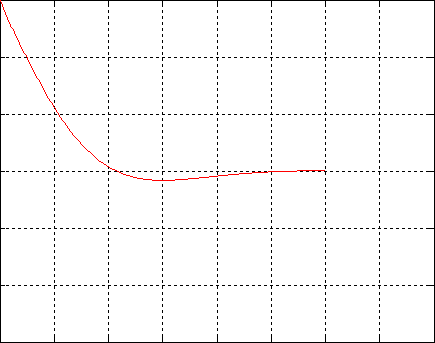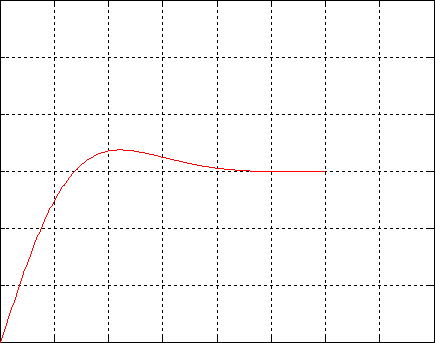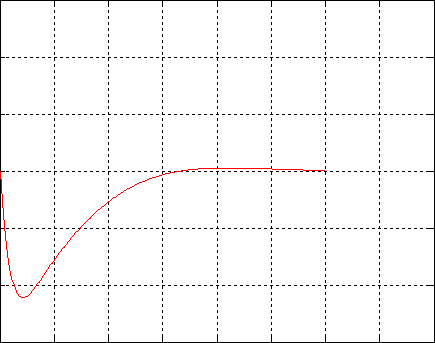
Representamos la temperatura en función del tiempo durante un periodo P=80 s en dos posiciones a lo largo de la barra x₁=15 cm y x₂=25 cm.

T0=15; %La amplitud de calentamiento-enfriamiento del extremo de la barra
P=80; %periodo
a2=8909; %Coeficiente, 1/alfa del cobre

x1=0.15; %dos posiciones en la barra
x2=0.25;
t=0:0.2:P; %tiempos 
T1=f_onda(T0,P,a2,x1,t);
T2=f_onda(T0,P,a2,x2,t);
plot(t,T1,'b',t,T2,'r')
title('Ondas térmicas')
xlabel('t (s)')
ylabel('Temperatura')
grid on
[xmax nmax]=max(abs(T1));
fprintf('El máximo de temperatura es %1.2f en el instante %1.2f, 
en la posición %1.2f\n',xmax,t(nmax),x1)
[xmax nmax]=max(abs(T2));
fprintf('El máximo de temperatura es %1.2f en el instante %1.2f,, 
en la posición %1.2f\n',xmax,t(nmax),x2)

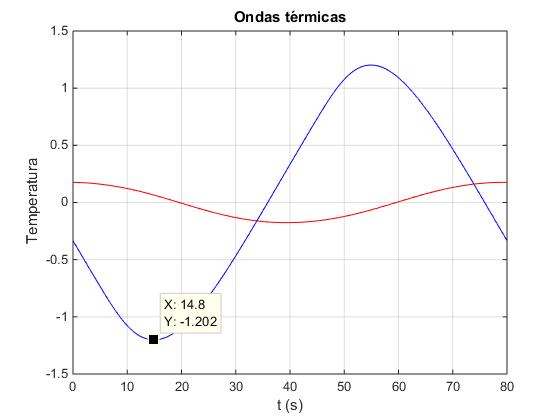
El máximo de temperatura es 1.20 en el instante 15.00, en la posición 0.15
El máximo de temperatura es 0.18 en el instante 39.40, en la posición 0.25

• El script nos devuelve la temperatura máxima o mínima A₁ y A₂, a partir de estos datos calculamos el coeficiente k de amortiguamiento de la amplitud. Podemos realizar estas medidas directamente en la representación gráfica utilizando la herramienta del menú Data cursor.

• El script nos devuelve los instantes t₁ y t₂ en el que se alcanzan estos valores máximos. Se mide la diferencia de tiempos Δt= t₂-t₁ que tarda el máximo o el mínimo en desplazarse desde la posición x₁ a la posición x₂, es decir, Δx=x₂-x₁

Los resultados obtenidos son los siguientes:

• En la posición x₁=15 cm (color azul) se alcanza el mínimo de temperatura en el instante t₁=15.0, la temperatura mínima es A₁=1.20.

• En la posición x₂=25 cm (color rojo) se alcanza el mínimo de temperatura en el instante t₂=39.4, la temperatura mínima es A₂=0.18.

El coeficiente k de amortiguamiento de la amplitud de la onda térmica vale

${\displaystyle k=\frac{1}{\Delta x}\ln \frac{A_1}{A_2}\text{,}k=\frac{1}{(0.25-0.15)}\ln \frac{1.20}{0.18}=19.0{\text{m}}^{\text{-1}}}$

La velocidad de propagación de las ondas térmicas en la barra de cobre es

${\displaystyle v=\frac{x_2-x_1}{t_2-t_1}\text{,}v=\frac{0.25-0.15}{39.4-15.0}=4.1·{10}^{-3}\text{m/s}}$

Calculamos el cociente

${\displaystyle \frac{v}{2k}=\alpha \text{,}\frac{4.1·{10}^{-3}}{2·19.0}=10.8·{10}^{-5}{\text{m}}^{\text{2}}\text{/s}}$

Comprobación

Los datos para el cobre son

• Densidad ρ=8900 kg/m³
• Calor específico c=390 J/(kg·K)
• Conductividad térmica K=389.6 W/(m·K)

El valor de α=K/(ρ·c)=11.22·10^-5 m²/s

Ondas térmicas

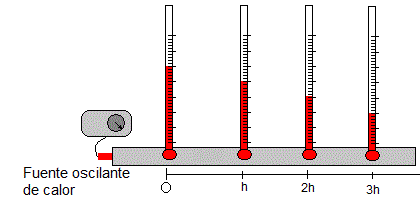
El experimento es similar, una larga barra metálica calentada peródicamente en su extremo izquierdo. Cuatro termopares registan la temperatura en función del tiempo en cada una de las posiciones, x=0, h=3.3 cm, 2h y 3h

La ecuación que describe la conducción termina en una dimensión es

${\displaystyle \frac{\partial T}{\partial t}=\alpha \frac{{\partial }^{2}T}{\partial x^2},\alpha =\frac{K}{\rho c}}$

En el estado estacionario, buscamos una solución de la forma

${\displaystyle T(x,t)=c_0(x)+{\displaystyle \sum _{n=\mathrm{1,2...}}^{\infty }{c}_n(x)}\cos \left({\omega }_{n}t-{\epsilon }_n\right)=c_0(x)+{\displaystyle \sum _{n=\mathrm{1,2...}}^{\infty }{c}_n(x)}\Re \left\{e^{i\left({\omega }_{n}t-{\epsilon }_n\right)}\right\}}$

El símbolo $\Re$, representa la parte real, ω_n=nω₁ son las frecuencias y ε_n son las fases

Introduciendo en la ecuación de la conducción del calor

${\displaystyle \begin{array}{l}\frac{d^2{c}_0(x)}{d{t}^2}+{\displaystyle \sum _{n=\mathrm{1,2...}}^{\infty }\frac{d^2{c}_n(x)}{d{t}^2}}{e}^{i\left({\omega }_{n}t-{\epsilon }_n\right)}={\displaystyle \sum _{n=\mathrm{1,2...}}^{\infty }\frac{i{\omega }_n}{\alpha }{c}_n(x)}{e}^{i\left({\omega }_{n}t-{\epsilon }_n\right)}\\ \{\begin{array}{l}\frac{d^2{c}_0(x)}{d{t}^2}=0\\ \frac{d^2{c}_n(x)}{d{t}^2}=\frac{i{\omega }_n}{\alpha }{c}_n(x)\end{array}\end{array}}$

Las soluciones de las dos ecuaciones diferenciales son

${\displaystyle \{\begin{array}{l}{c}_0(x)=P_{1}x+P_0\\ c_n(x)=A_n\exp \left(\sqrt{\frac{i{\omega }_n}{\alpha }}x\right)+B_n\exp \left(-\sqrt{\frac{i{\omega }_n}{\alpha }}x\right)\end{array}}$

Teniendo en cuenta las raíces de la unidad imaginaria

${\displaystyle \sqrt{i}=\{\begin{array}{l}\frac{1}{\sqrt{2}}+i\frac{1}{\sqrt{2}}\\ -\frac{1}{\sqrt{2}}-i\frac{1}{\sqrt{2}}\end{array}}$

El resultado es

${\displaystyle \{\begin{array}{l}{c}_0(x)=P_{1}x+P_0\\ c_n(x)=A_n\exp \left(\left(1+i\right)\sqrt{\frac{n{\omega }_1}{2\alpha }}x\right)+B_n\exp \left(-\left(1+i\right)\sqrt{\frac{n{\omega }_1}{2\alpha }x}\right)\end{array}}$

Para que las temperaturas sea finitas cuando x→∞, se tiene que cumplir que A_n=0 para todo n

${\displaystyle \begin{array}{l}T(x,t)=\left(P_{1}x+P_0\right)+{\displaystyle \sum _{n=\mathrm{1,2...}}^{\infty }{B}_n\exp \left(-\left(1+i\right)\sqrt{\frac{n{\omega }_1}{2\alpha }}x\right)}\exp i\left(n{\omega }_{1}t-{\epsilon }_n\right)\\ T(x,t)=\left(P_{1}x+P_0\right)+{\displaystyle \sum _{n=\mathrm{1,2...}}^{\infty }{B}_n\exp \left(-\sqrt{\frac{n{\omega }_1}{2\alpha }}x\right)\exp \left[i\left(n{\omega }_{1}t-\sqrt{\frac{n{\omega }_1}{2\alpha }}x-{\epsilon }_n\right)\right]}\end{array}}$

Para x=0 la temperatura es

${\displaystyle T(\mathrm{0,}t)=P_0+{\displaystyle \sum _{n=\mathrm{1,2...}}^{\infty }{B}_n\exp \left[i\left(n{\omega }_{1}t-{\epsilon }_n\right)\right]}}$

La parte real

${\displaystyle T(\mathrm{0,}t)=P_0+{\displaystyle \sum _{n=\mathrm{1,2...}}^{\infty }{B}_n\cos \left(n{\omega }_{1}t-{\epsilon }_n\right)}}$

Cálculo de los coeficientes

Se observa que el primer termopar situado en x=0, registra una temperatura que varía con el tiempo, en el estado estacionario, de la forma

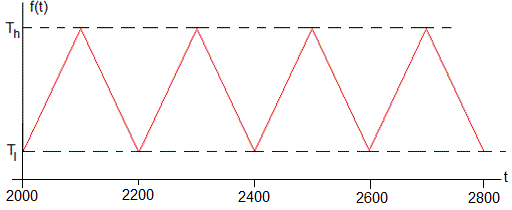
Se trata de una función periódica de forma triangular de periodo 200 s. La temperatura fluctúa entre T_h=84 °C, y T_l=72 °C. Vamos a realizar el análisis de Fourier de la función periódica f(t)

${\displaystyle f(t)=\{\begin{array}{l}{T}_h+\frac{T_h-T_l}{P}t,-P\le t<0\\ T_l-\frac{T_h-T_l}{P}\left(t-P\right),0\le t<P\end{array}}$

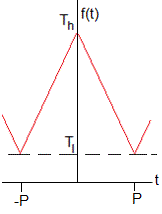
Toda función f(t) periódica de periodo 2P, se puede representar en forma de una suma infinita de funciones armónicas

${\displaystyle f(t)=\frac{a_0}{2}+{\displaystyle \sum _{k=1}^{\infty }\left(a_k\cos \frac{k\pi t}{P}+b_k\sin \frac{k\pi t}{P}\right)}}$

f(t) es una función par, f(t)=f(-t), los términos b_k son nulos

${\displaystyle a_0=\frac{1}{P}{\displaystyle \underset{-P}{\overset{P}{\int }}f(t)dt}=\frac{1}{P}\left\{{\displaystyle \underset{-P}{\overset{0}{\int }}\left(T_h+\frac{T_h-T_l}{P}t\right)}dt+{\displaystyle \underset{0}{\overset{P}{\int }}\left(T_l-\frac{T_h-T_l}{P}\left(t-P\right)\right)}dt\right\}=T_h+T_l}$

Los otros coeficientes

${\displaystyle \begin{array}{l}{a}_k=\frac{1}{P}\left\{{\displaystyle \underset{-P}{\overset{0}{\int }}\cos \frac{k\pi t}{P}\left(T_h+\frac{T_h-T_l}{P}t\right)}dt+{\displaystyle \underset{0}{\overset{P}{\int }}\cos \frac{k\pi t}{P}\left(T_l-\frac{T_h-T_l}{P}\left(t-P\right)\right)}dt\right\}\\ a_k=\frac{1}{P}\left\{T_h{\displaystyle \underset{-P}{\overset{0}{\int }}\cos \frac{k\pi t}{P}}dt+\frac{T_h-T_l}{P}{\displaystyle \underset{-P}{\overset{0}{\int }}t\cos \frac{k\pi t}{P}dt}+T_l{\displaystyle \underset{0}{\overset{P}{\int }}\cos \frac{k\pi t}{P}dt-}\frac{T_h-T_l}{P}{\displaystyle \underset{0}{\overset{P}{\int }}t\cos \frac{k\pi t}{P}dt+\left(T_h-T_l\right){\displaystyle \underset{0}{\overset{P}{\int }}\cos \frac{k\pi t}{P}dt}}\right\}\end{array}}$

Las integrales valen

${\displaystyle \begin{array}{l}{\displaystyle \int \cos \frac{k\pi t}{P}dt=\frac{P}{k\pi }\sin \frac{k\pi t}{P}}\\ {\displaystyle \int t\cos \frac{k\pi t}{P}dt,}\{\begin{array}{l}u=t,du=dt\\ dv=\cos \frac{k\pi t}{P}dt,v=\frac{P}{k\pi }\sin \frac{k\pi t}{P}\end{array}\\ =\frac{P}{k\pi }t\sin \frac{k\pi t}{P}-\frac{P}{k\pi }{\displaystyle \int \sin \frac{k\pi t}{P}dt=\frac{P}{k\pi }t\sin \frac{k\pi t}{P}+\frac{P^2}{k^2{\pi }^2}\cos \frac{k\pi t}{P}}\end{array}}$

El resultado es

${\displaystyle \begin{array}{l}{a}_k=\frac{1}{P}\left\{0+\frac{T_h-T_l}{P}\left(\frac{P^2}{k^2{\pi }^2}\left(1-\cos \left(k\pi \right)\right)\right)+0-\frac{T_h-T_l}{P}\left(\frac{P^2}{k^2{\pi }^2}\left(\cos \left(k\pi \right)-1\right)\right)+0\right\}=2\frac{1-\cos \left(k\pi \right)}{k^2{\pi }^2}\left(T_h-T_l\right)\\ a_k=\{\begin{array}{l}\mathrm{0,}k=\mathrm{2,4,6...}\\ \frac{4}{k^2{\pi }^2}\left(T_h-T_l\right),k=\mathrm{1,3,5...}\end{array}\end{array}}$

La función periódica f(t) se expresa

${\displaystyle f(t)=\frac{T_h+T_l}{2}+\frac{4}{{\pi }^2}\left(T_h-T_l\right){\displaystyle \sum _{k=\mathrm{1,3,5...}}^{\infty }\frac{1}{k^2}\cos \frac{k\pi t}{P}}}$

Th=84;
Tl=72;
P=100; %2P es el periodo, 200 s
hold on
%función periódica
line([-P,0],[Tl,Th])
line([0,P],[Th,Tl])
%serie de Fourier
x=linspace(-P,P,100);
y=zeros(length(x),1);
n=3; %terminos del desarrollo en serie
for i=1:length(x)
    y(i)=(Th+Tl)/2;
    for k=1:2:n
        y(i)=y(i)+4*(Th-Tl)*cos(k*pi*x(i)/P)/(k^2*pi^2);
     end
end
plot(x,y, 'r');
title('Aproximación de Fourier')
xlabel('t'); 
ylabel('f(t)')

Con k=1, 3 el ajuste es notable

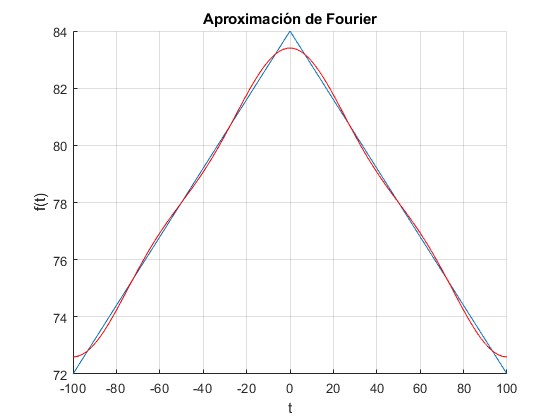
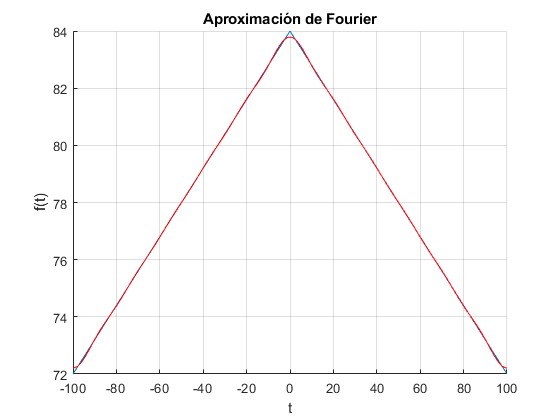
Con k=1, 3, 5, 7, 9, 11 el ajuste es casi completo, excepto en el vértice

Calculamos los coeficientes P₀ y B_n en el primer termopar

${\displaystyle \begin{array}{l}T(\mathrm{0,}t)=P_0+{\displaystyle \sum _{n=\mathrm{1,2...}}^{\infty }{B}_n\cos \left(n{\omega }_{1}t-{\epsilon }_n\right)}=\frac{T_h+T_l}{2}+\frac{4}{{\pi }^2}\left(T_h-T_l\right){\displaystyle \sum _{n=\mathrm{1,3,5...}}^{\infty }\frac{1}{n^2}\cos \frac{n\pi t}{P}}\\ \{\begin{array}{l}{P}_0=\frac{T_h+T_l}{2}\\ B_n=\mathrm{0,}n=\mathrm{2,4,6...}\\ B_n=\frac{4}{{\pi }^2{n}^2}\left(T_h-T_l\right),n=\mathrm{1,3,5...}\\ {\omega }_1=\frac{\pi }{P}\\ {\epsilon }_n=0\end{array}\end{array}}$

Onda térmica

La onda térmica se expresa

${\displaystyle \begin{array}{l}T(x,t)=P_{1}x+\frac{T_h+T_l}{2}+\frac{4}{{\pi }^2}\left(T_h-T_l\right){\displaystyle \sum _{n=\mathrm{1,3,5...}}^{\infty }\frac{1}{n^2}\exp \left(-\frac{x}{d_n}\right)\exp \left[i\left(n\frac{\pi }{P}t-\frac{x}{d_n}\right)\right]}\\ d_n=\sqrt{\frac{2\alpha P}{n\pi }}\end{array}}$

La amplitud de la onda térmica se amortigua con la distancia. Tomando la parte real

${\displaystyle T(x,t)=P_{1}x+\frac{T_h+T_l}{2}+\frac{4}{{\pi }^2}\left(T_h-T_l\right){\displaystyle \sum _{n=\mathrm{1,3,5...}}^{\infty }\frac{1}{n^2}\exp \left(-\frac{x}{d_n}\right)\cos \left(n\frac{\pi }{P}t-\frac{x}{d_n}\right)}}$

Queda pendiente por determinar el coeficiente P₁. Tomando el valor medio de la temperaturas en el segundo termopar, x=h

${\displaystyle \begin{array}{l}\langle T(h,t)\rangle =P_{1}h+\frac{T_h+T_l}{2}+\frac{4}{{\pi }^2}\left(T_h-T_l\right){\displaystyle \sum _{n=\mathrm{1,3,5...}}^{\infty }\frac{1}{n^2}\exp \left(-\frac{h}{d_n}\right)\langle \cos \left(n\frac{\pi }{P}t-\frac{h}{d_n}\right)\rangle }\\ \langle T(h,t)\rangle =P_{1}h+\langle T(\mathrm{0,}t)\rangle \\ P_1=\frac{\langle T(h,t)\rangle -\langle T(\mathrm{0,}t)\rangle }{h}\end{array}}$

El valor medio de la función periódica, seno o coseno es cero. <T(0,t)>=(T_h+T_l)/2 es el valor medio de las temperaturas en el primer termopar situado en x=0

Ejemplo

• Primer termopar: T_h=84, T_l=72. Temperatura media 78 °C
• Segundo termopar, la temperatura media es algo inferior, por ejemplo, 74 °C. El coeficiente P₁=(74-78)/0.033
• El periodo es 200 s, medio periodo es P=100 s
• El coeficiente α=1.02·10^-4 m²/s para el cobre

Representamos la función T(x,t) en las posiciones x=0, 3.3, 6.6 y 9.9 cm, en el estado estacionario, durante cuatro periodos, 800 s

Th=84;
Tl=72;
P1=-400/3.3; %coeficiente
P=100; %medio periodo
hold on
t=linspace(0,800,200);
y=zeros(length(t),1);
n=11; %terminos del desarrollo en serie
for x1=(0:3.3:9.9)/100 %posición del termopar
    for i=1:length(t)
        y(i)=(Th+Tl)/2+P1*x1;
        for k=1:2:n
            d=sqrt(1.02e-4*2*P/(k*pi));
            y(i)=y(i)+4*(Th-Tl)*exp(-x1/d)*cos(k*pi*t(i)/P-x1/d)/(k^2*pi^2);
        end
    end
    plot(t,y);
end
title('Ondas térmicas')
xlabel('t'); 
ylabel('T(x,t)')
grid on
hold off

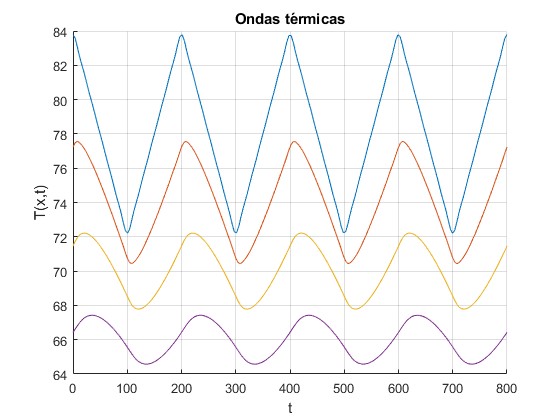
Las conclusiones que podemos extraer de este ejemplo son

• La temperatura registrada por un termopar no es constante sino que oscila con el tiempo alrededor de su valor medio.

• La temperatura media registrada por un termopar, se incrementa hasta que alcanza un valor constante en el estado estacionario. La temperatura media final no es la misma en todos los termopares, es más pequeña en los más alejados, lo que indica que el calor fluye desde la parte más caliente a la más fría

• El termopar más cercano a la fuente de calor, registra una variación de temperatura con el tiempo de forma casi triangular (primera función) que tiende hacia la forma armónica (seno o coseno) para los termopares más alejados de la fuente (última función)

• Hay una diferencia de fase entre los termopares, por el ejemplo, el máximo de temperatura no se produce en el mismo instante, se produce más tarde para el termopar más alejado

Referencias

Bodas A, Gandía V., E. López-Baeza. An undergraduate experiment on the propagation of thermal waves. Am. J. Phys. 66 (6) June 1998, pp. 528-533.

Muhammad Sabieh Anwar, Junaid Alam, Muhammad Wasif, Rafi Ullah, Sohaib Shamim, Wasif Zia. Fourier analysis of thermal diffusive waves. Am. J. Phys. 82 (10), October 2014. pp. 928-933