El extremo izquierdo se mantiene a temperatura constante

Supongamos una varilla metálica de longitud L, que se ha calentado a una temperatura T₀, uno de sus extremos x=0, se mantiene a temperatura elevada T_a y el otro extremo x=L radia calor al ambiente, cuya temperatura es T_s.

Para calcular la temperatura T(x,t) en un punto x de la varilla y en un instante t, resolvemos la ecuación de la conducción del calor

${\displaystyle \frac{1}{\alpha }\frac{\partial T}{\partial t}=\frac{{\partial }^{2}T}{\partial x^2}0<x<Lt>0}$

La condición de contorno en el extremo izquierdo x=0, es T(0,t)=T_a

La condición de contorno en el extremo derecho x=L, es

${\displaystyle {-\frac{\partial T(x,t)}{\partial x}|}_{x=L}=h\left(T(L,t)-T_s\right)}$

La condición inicial, es la de una varilla a temperatura uniforme T(x,0)=T₀

El estado estacionario

Al cabo de cierto tiempo, teóricamente infinito, que en la práctica depende del tipo de material que empleamos, se establece un estado estacionario en el que la temperatura de cada punto de la varilla no varía con el tiempo.

${\displaystyle \begin{array}{l}\frac{{\partial }^{2}T}{\partial x^2}=0\\ T(x)=Ax+B\end{array}}$

donde A y B se determinan a partir de las condiciones de contorno en x=0

T(0)=T_a. El coeficiente B=T_a

y en x=L

${\displaystyle -a=h(aL+B-T_s)}$

Despejamos A y B del sistema de dos ecuaciones

${\displaystyle T(x,\infty )=-h\frac{T_a-T_s}{1+hL}x+T_a}$

Solución de la ecuación de la conducción del calor

Definimos la función u(x,t)=T(x,t)-T(x,∞), en términos de esta nueva función, la ecuación de la conducción del calor se escibe,

${\displaystyle \frac{1}{\alpha }\frac{\partial u}{\partial t}=\frac{{\partial }^{2}u}{\partial x^2}0<x<Lt>0}$

Condición inicial

u(x,0)=T(x,0)-T(x,∞)

${\displaystyle u(x\mathrm{,0})=T_0+h\frac{T_a-T_s}{1+hL}x-T_a}$

Condiciones de contorno

En el extremo izquierdo, x=0

u(0,t)=T(0,t)-T(0,∞)

u(0,t)=T_a-T_a=0

En el extremo derecho, x=L

${\displaystyle \begin{array}{l}{\frac{\partial u(x,t)}{\partial x}|}_{x=L}={\frac{\partial T(x,t)}{\partial x}|}_{x=L}-{\frac{\partial T(x,\infty )}{\partial x}|}_{x=L}\\ {\frac{\partial u(x,t)}{\partial x}|}_{x=L}=-h\left(T(L,t)-T_s\right)+h\frac{T_a-T_s}{1+hL}\\ {\frac{\partial u(x,t)}{\partial x}|}_{x=L}=-h\left(u(L,t)+T(L,\infty )-T_s\right)+h\frac{T_a-T_s}{1+hL}\\ {\frac{\partial u(x,t)}{\partial x}|}_{x=L}=-h\left(u(L,t)-h\frac{T_a-T_s}{1+hL}L+T_a-T_s\right)+h\frac{T_a-T_s}{1+hL}\\ {\frac{\partial u(x,t)}{\partial x}|}_{x=L}=-hu(L,t)\end{array}}$

Variables separadas

Buscamos una solución de la forma u(x, t)=F(x)·G(t), variables separadas

${\displaystyle \frac{1}{\alpha }\frac{1}{G(t)}\frac{dG(t)}{dt}=\frac{1}{F(x)}\frac{d^{2}F(x)}{d{x}^2}=-{\omega }^2}$

Integramos la primera ecuación diferencial

${\displaystyle \begin{array}{l}\frac{dG(t)}{dt}+\alpha {\omega }^{2}G(t)=0\\ G(t)=G(0)·\exp \left(-\alpha {\omega }^{2}t\right)\end{array}}$

Integramos la segunda ecuación diferencial

${\displaystyle \frac{d^{2}F(x)}{d{x}^2}+{\omega }^{2}F(x)=0}$

Es una ecuación diferencial similar a la de un Movimiento Armónico Simple, cuya solución es F(x)=Asin(ωx)+Bcos(ωx)

Solución general

• En el extremo izquierdo de la varilla x=0, u(0, t)=0, F(0)=0, por lo que B=0. F(x)=Asin(ωx)

• En el extremo derecho de la varilla x=L, la derivada F(x) debe cumplir que, ωAcos(ωL)=-hAsin(ωL)=0, o bien, kcos(k)+hLsin(k)=0, donde k=ωL

La solución completa u(x,t) es la superposición

${\displaystyle u(x,t)={\displaystyle \sum _{n=1}^{\infty }{A}_n\sin \left(k_n\frac{x}{L}\right)\exp \left(-\alpha \frac{k_n^2}{L^2}t\right)}}$

k_n son las raíces de la ecuación transcendente, kcos(k)+hLsin(k)=0

Coeficientes A_n

Solamente, queda por determinar los coeficientes A_n, identificando la solución para t=0 con la condición inicial u(x,0)

${\displaystyle \begin{array}{l}u(x\mathrm{,0})={\displaystyle \sum _{n=1}^{\infty }{A}_n\sin \left(k_n\frac{x}{L}\right)}u(x\mathrm{,0})=h\frac{T_a-T_s}{1+hL}x+T_0-T_a\\ {\displaystyle \sum _{n=1}^{\infty }{A}_n\sin \left(k_n\frac{x}{L}\right)}=ax+ba=h\frac{T_a-T_s}{1+hL}b=T_0-T_a\end{array}}$

Teniendo en cuenta la relación de ortogonalidad, véase más abajo

${\displaystyle {\displaystyle \underset{0}{\overset{L}{\int }}\sin \left(k_n\frac{x}{L}\right)}\sin \left(k_m\frac{x}{L}\right)dx=0n\ne m}$

Obtenemos los coeficientes A_n

${\displaystyle \begin{array}{l}\begin{array}{l}{A}_n=\frac{{\displaystyle \underset{0}{\overset{L}{\int }}(ax+b)\sin \left(k_{n}x/L\right)dx}}{{\displaystyle \underset{0}{\overset{L}{\int }}{\sin }^2\left(k_{n}x/L\right)dx}}\\ {\displaystyle \underset{0}{\overset{L}{\int }}{\sin }^2\left(k_{n}x/L\right)dx}=\frac{L}{2}\left(1-\frac{1}{2k_n}\sin \left(2k_n\right)\right)=\frac{L}{2k_n^2}\left(k_n^2+hL{\sin }^2\left(k_n\right)\right)\\ {\displaystyle \underset{0}{\overset{L}{\int }}\sin \left(k_{n}x/L\right)dx}=2\frac{L}{k_n}{\sin }^2\left(\frac{k_n}{2}\right)\end{array}\hfill \\ {\displaystyle \underset{0}{\overset{L}{\int }}x\sin \left(k_{n}x/L\right)dx}=\frac{L^2}{k_n}\left(\frac{\sin \left(k_n\right)}{k_n}-\cos \left(k_n\right)\right)=\frac{L^2}{k_n^2}\sin \left(k_n\right)(1+hL)\hfill \end{array}}$

Para obtener estos resultados, se ha tenido en cuenta que k_n son las raíces de la ecuación transcendente kcos(k)+hLsin(k)=0

${\displaystyle A_n=2\frac{aL(1+hL)\sin \left(k_n\right)+2b{k}_n{\sin }^2\left(\frac{k_n}{2}\right)}{k_n^2+hL{\sin }^2\left(k_n\right)}}$

Solución completa

La solución completa es

${\displaystyle \begin{array}{l}u(x,t)={\displaystyle \sum _{n=1}^{\infty }{A}_n\sin \left(k_n\frac{x}{L}\right)\exp \left(-\alpha \frac{k_n^2}{L^2}t\right)}\hfill \\ \begin{array}{l}T(x,t)=u(x,t)+T(x,\infty )=\\ {\displaystyle \sum _{n=1}^{\infty }2\frac{aL(1+hL)\sin \left(k_n\right)+2b{k}_n{\sin }^2\left(\frac{k_n}{2}\right)}{k_n^2+hL{\sin }^2\left(k_n\right)}\sin \left(k_n\frac{x}{L}\right)\exp \left(-\alpha \frac{k_n^2}{L^2}t\right)-ax+T_0-b}\end{array}\hfill \\ a=h\frac{T_a-T_s}{1+hL}b=T_0-T_a\hfill \end{array}}$

Ejemplo

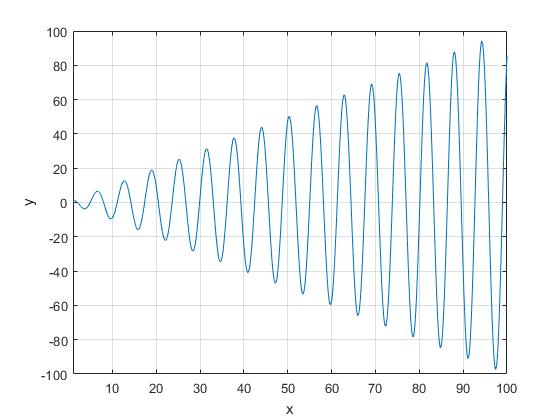
Supongamos que h=1 y L=1, vamos a representar gráficamente la función y=xcos(x)+hLsin(x), para estimar aproximadamente donde se encuentran las raíces de la ecuación transcendente. Cambiamos el valor del parámetro hL para ver el efecto sobre las raíces

>> hL=1;
>> f=@(x) x*cos(x)+h*L*sin(x);
>> fplot(f,[1,100])
>> grid on
>> xlabel('x')
>> ylabel('y')

La función raices calcula las raíces múltiples de la función f(x) buscando los intervalos en los que dicha función cambia de signo y utilizando la función MATLAB fzero para encontrarlas

function r = raices(f, x)
    y=f(x);
    indices=find(y(1:end-1).*y(2:end)<0);
    r=zeros(1,length(indices));
    for k=1:length(indices)
        r(k)=fzero(f, [x(indices(k)), x(indices(k)+1)]);
    end
end

Una vez obtenidas las raíces k_n de la ecuación transcendente, comprobamos las relaciones de ortogonalidad entre las funciones sin(k_nx/L) y sin(k_mx/L) con m≠n

>> f=@(x) sin(k(1)*x/L).*sin(k(2)*x/L);
>> integral(f,0,L)
ans =  -6.9389e-17
>> f=@(x) sin(k(5)*x/L).*sin(k(9)*x/L);
>> integral(f,0,L)
ans =     0

Definimos la función temperatura_11 para calcular la distribución de temperaturas a lo largo de la varilla en el instante t

function [x,T]=temperatura_11(T0,Ts,TA, h, L,k,a2,t)
   x=linspace(0,L,100);
   if(t==0)
       T=T0*ones(1,length(x));
       return;
   end
   
   a=h*(TA-Ts)/(1+h*L);
   b=T0-TA;
   T=(-a*x+T0-b).*ones(1,length(x));
   for n=1:length(k)
        an=2*(a*L*(1+h*L)*sin(k(n))+2*b*k(n)*sin(k(n)/2)^2)/(k(n)^2+h*L*sin(k(n))^2);
        T=T+an*exp(-k(n)^2*t/(a2*L^2))*sin(k(n)*x/L);
   end
end

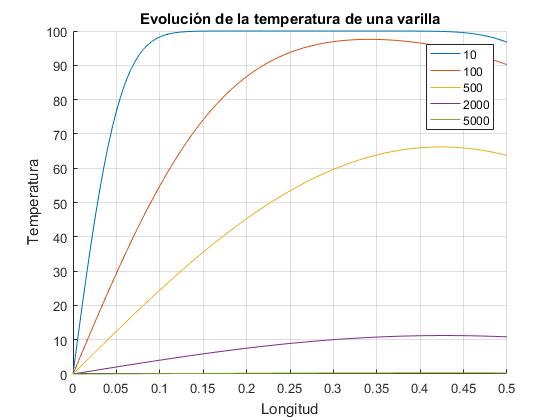
Creamos un script en el que establecemos la temperatura inicial T₀, la temperatura ambiente T_s, la temperatura T_a del extremos izquierdo x=0, la longitud de la varilla L, el material del cual está hecho la varilla, (parámetro α), el coeficiente de pérdida de calor por radiación h. El script calcula un número elevado de raíces k_n de la ecuación transcendente y representa la distribución de temperaturas de la varilla en varios instantes. Se sugiere al lector cambiar el valor del parámetro h y observar el efecto sobre la distribución de temperaturas en la varilla

T0=100; %temperatura inicial
Ts=0; %temperatura ambiente (final)
TA=Ts; %temperatura en el extremo izquierdo
h=1; %pérdida de calor por radiación
L=0.5; % longitud de la varilla
alfa=11352; %Coeficiente, 1/alfa del aluminio

f=@(x) x.*cos(x)+h*L*sin(x);
x=linspace(0,400,400);
k=raices(f,x);

%instantes
t=[10 100 500 2000, 5000];
hold on
for i=1:length(t)
    [x,T]=temperatura_11(T0,Ts,TA, h, L,k,alfa,t(i));
    plot(x,T,'displayName',num2str(t(i)));
end
title('Evolución de la temperatura de una varilla')
xlabel('Longitud')
ylabel('Temperatura')
legend('-DynamicLegend','location','northeast')
grid on
hold off  

Cambiamos la temperatura T_a del extremo izquierdo x=0, de la varilla, y la temperatura inicial T₀

Ts=20; %temperatura ambiente (final)
T0=Ts; %temperatura inicial
TA=100; %temperatura en el extremo izquierdo
h=1; %pérdida de calor por radiación
L=0.5; % longitud de la varilla
alfa=11352; %Coeficiente, 1/alfa del aluminio
....

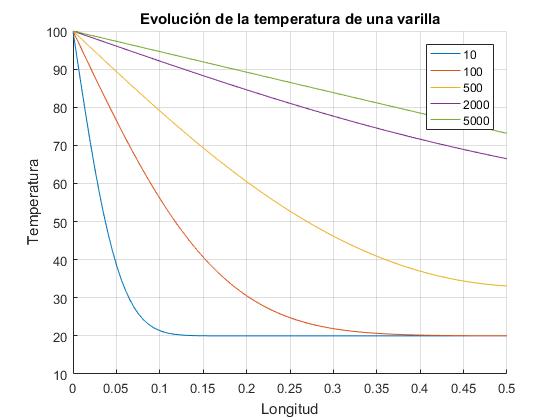
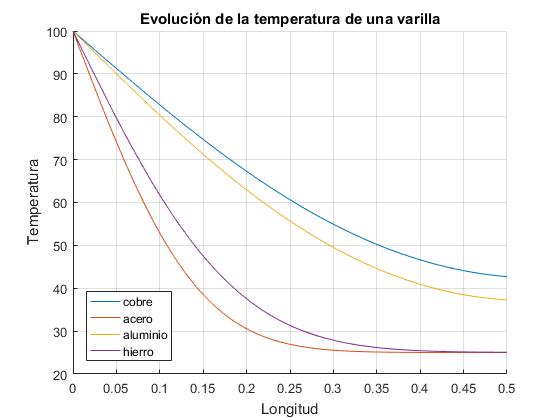
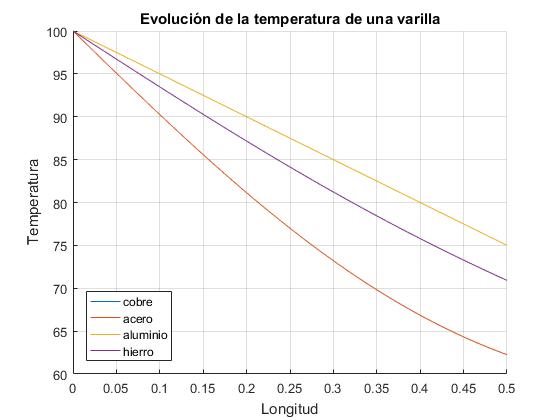
Con este script comparamos el comportamiento de cuatro materiales: cobre, aluminio, hierro y acero en el instante t=500 s. La temperatura inicial de la barra T₀ es la temperatura ambiente T_s=25°. La temperatura del extremo x=0 de la barra es T_a=100°. La longitud de la barra es L=0.5 m

Ts=25; %temperatura ambiente (final)
T0=Ts; %temperatura inicial
TA=100; %temperatura en el extremo izquierdo
h=1; %pérdida de calor por radiación
L=0.5; % longitud de la varilla

f=@(x) x.*cos(x)+h*L*sin(x);
x=linspace(0,400,400);
k=raices(f,x);
t=500;
alfa=[8909,79733,11352,47661]; %materiales
hold on
%axis([0 0.5 -5 100]);
for i=1:length(alfa)
    [x,T]=temperatura_11(T0,Ts,TA, h, L,k,alfa(i),t);
    plot(x,T);
end
hold off  
title('Evolución de la temperatura de una varilla')
xlabel('Longitud')
ylabel('Temperatura')
legend('cobre','acero','aluminio','hierro','location','southwest')
grid on

Cerca del estado estacionario t=10000 s, para el aluminio y el cobre

El extremo izquierdo está aislado

Supongamos una varilla metálica de longitud L, que se ha calentado a una temperatura T₀, el extremo izquierdo x=0, se mantiene aislado y el otro extremo x=L radia calor al ambiente, cuya temperatura es T_s. Este sistema podría simular un termo abierto que contiene un líquido a una temperatura mayor o menor que la ambiente.

Para calcular la temperatura T(x,t) en un punto x de la varilla y en un instante t, resolvemos la ecuación de la conducción del calor

${\displaystyle \frac{1}{\alpha }\frac{\partial T}{\partial t}=\frac{{\partial }^{2}T}{\partial x^2}0<x<Lt>0}$

La condición de contorno en el extremo izquierdo x=0, (aislado) es

${\displaystyle {\frac{\partial T(x,t)}{\partial x}|}_{x=0}=0}$

La condición de contorno en el extremo derecho x=L, (radia calor) es

${\displaystyle {-\frac{\partial T(x,t)}{\partial x}|}_{x=L}=h\left(T(L,t)-T_s\right)}$

La condición inicial, es la de una varilla a temperatura uniforme T(x,0)=T₀

El estado estacionario

Al cabo de cierto tiempo, teóricamente infinito, que en la práctica depende del tipo de material que empleamos, se establece un estado estacionario en el que la temperatura de cada punto de la varilla no varía con el tiempo. La ecuación de la conducción del calor independiente del tiempo y las condiciones de contorno son

${\displaystyle \frac{{\partial }^{2}T}{\partial x^2}=0\{\begin{array}{l}{\frac{\partial T(x)}{\partial x}|}_{x=0}=0\\ -{\frac{\partial T(x)}{\partial x}|}_{x=L}=h(T(L)-T_s)\end{array}}$

El estado estacionario se caracteriza por una temperatura uniforme de la barra igual a la temperatura ambiente, T(x,∞)=T_s

Solución de la ecuación de la conducción del calor

Definimos la función u(x,t)=T(x,t)-T(x,∞), en términos de esta nueva función, la ecuación de la conducción del calor se escibe,

${\displaystyle \frac{1}{\alpha }\frac{\partial u}{\partial t}=\frac{{\partial }^{2}u}{\partial x^2}0<x<Lt>0}$

Condición inicial

u(x,0)=T(x,0)-T(x,∞)=T₀-T_s

Condiciones de contorno

En el extremo izquierdo, x=0

${\displaystyle {\frac{\partial u(x,t)}{\partial x}|}_{x=0}=0}$

En el extremo derecho, x=L

${\displaystyle {-\frac{\partial u(x,t)}{\partial x}|}_{x=L}=h·u(L,t)}$

Variables separadas

Buscamos una solución de la forma u(x, t)=F(x)·G(t), variables separadas

${\displaystyle \frac{1}{\alpha }\frac{1}{G(t)}\frac{dG(t)}{dt}=\frac{1}{F(x)}\frac{d^{2}F(x)}{d{x}^2}=-{\omega }^2}$

Integramos la primera ecuación diferencial

${\displaystyle \begin{array}{l}\frac{dG(t)}{dt}+\alpha {\omega }^{2}G(t)=0\\ G(t)=G(0)·\exp \left(-\alpha {\omega }^{2}t\right)\end{array}}$

Integramos la segunda ecuación diferencial

${\displaystyle \frac{d^{2}F(x)}{d{x}^2}+{\omega }^{2}F(x)=0}$

Es una ecuación diferencial similar a la de un Movimiento Armónico Simple, cuya solución es F(x)=Asin(ωx)+Bcos(ωx)

Solución general

• En el extremo izquierdo de la varilla x=0, la derivada de F(x) respecto de x es nula, por lo que A=0. F(x)=Bcos(ωx)

• En el extremo derecho de la varilla x=L, la derivada F(x) debe cumplir que, ωBsin(ωL)=hBcos(ωL)=0, o bien, ksin(k)-hLcos(k)=0, donde k=ωL

La solución completa u(x,t) es la superposición

${\displaystyle u(x,t)={\displaystyle \sum _{n=1}^{\infty }{B}_n\cos \left(k_n\frac{x}{L}\right)\exp \left(-\alpha \frac{k_n^2}{L^2}t\right)}}$

k_n son las raíces de la ecuación transcendente, ksin(k)-hLcos(k)=0

Coeficientes B_n

Solamente, queda por determinar los coeficientes B_n, identificando la solución para t=0 con la condición inicial u(x,0)

${\displaystyle \begin{array}{l}u(x\mathrm{,0})={\displaystyle \sum _{n=1}^{\infty }{B}_n\cos \left(k_n\frac{x}{L}\right)}\hfill \\ T_0-T_s={\displaystyle \sum _{n=1}^{\infty }{B}_n\cos \left(k_n\frac{x}{L}\right)}\hfill \end{array}}$

Teniendo en cuenta la relación de ortogonalidad,

${\displaystyle {\displaystyle \underset{0}{\overset{L}{\int }}\cos \left(k_n\frac{x}{L}\right)}\cos \left(k_m\frac{x}{L}\right)dx=0n\ne m}$

Obtenemos los coeficientes B_n

${\displaystyle \begin{array}{l}\begin{array}{l}{B}_n=\frac{{\displaystyle \underset{0}{\overset{L}{\int }}(T_0-T_s)\cos (k_{n}x/L)dx}}{{\displaystyle \underset{0}{\overset{L}{\int }}{\cos }^2(k_{n}x/L)dx}}\hfill \\ {\displaystyle \underset{0}{\overset{L}{\int }}{\cos }^2(k_{n}x/L)dx}=\frac{L}{2}\left(1+\frac{1}{2k_n}\sin (2k_n)\right)\hfill \\ {\displaystyle \underset{0}{\overset{L}{\int }}\cos (k_{n}x/L)dx}=\frac{L}{k_n}\sin \left(k_n\right)\hfill \end{array}\hfill \\ B_n=4(T_0-T_s)\frac{\sin \left(k_n\right)}{2k_n+\sin (2k_n)}\hfill \end{array}}$

Solución completa

La solución completa es

${\displaystyle \begin{array}{l}u(x,t)={\displaystyle \sum _{n=1}^{\infty }{B}_n\cos \left(k_n\frac{x}{L}\right)\exp \left(-\alpha \frac{k_n^2}{L^2}t\right)}\\ T(x,t)=u(x,t)+T(x,\infty )=u(x,t)+T_s\\ T(x,t)=T_s+4(T_0-T_s){\displaystyle \sum _{n=1}^{\infty }\frac{\sin \left(k_n\right)}{2k_n+\sin (2k_n)}\cos \left(k_n\frac{x}{L}\right)\exp \left(-\alpha \frac{k_n^2}{L^2}t\right)}\end{array}}$

Definimos la función temperatura_12 para calcular la distribución de temperaturas en función del tiempo t para una posición x de la varilla

function [t,T]=temperatura_12(T0,Ts, h, L,k,a2,x)
   t=linspace(0,500,200);   
    T=Ts;
   for n=1:length(k)
        an=4*(T0-Ts)*sin(k(n))/(2*k(n)+sin(2*k(n)));
        T=T+an*exp(-k(n)^2*t/(a2*L^2))*cos(k(n)*x/L);
   end
end

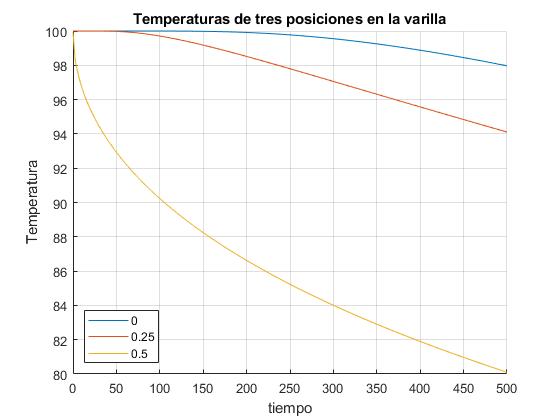
Creamos un script en el que establecemos la temperatura inicial T₀, la temperatura ambiente T_s, la longitud de la varilla L, el material del cual está hecho la varilla, (parámetro α), el coeficiente de pérdida de calor por radiación h. El script calcula un número elevado de raíces k_n de la ecuación transcendente y representa la evolución de la temperatura en tres posiciones de la varilla: extremo izquierdo, x=0, medio, x=L/2 y extremo derecho x=L. Se sugiere al lector cambiar el material del que está hecho la varilla, el valor del parámetro h, la temperatura inicial T₀ de la varilla y la ambiente, T_sy observar el efecto

T0=100; %temperatura inicial
Ts=0; %temperatura ambiente (final)
h=1; %pérdida de calor por radiación
L=0.5; % longitud de la varilla
alfa=11352; %Coeficiente, 1/alfa del aluminio

f=@(x) x.*sin(x)-h*L*cos(x);
x=linspace(0,400,400);
k=raices(f,x);

%posiciones
x=[0, L/2, L];
hold on
for i=1:length(x)
    [t,T]=temperatura_12(T0,Ts, h, L,k,alfa,x(i));
    plot(t,T,'displayName',num2str(x(i)));
end
title('Temperaturas de tres posiciones en la varilla')
xlabel('tiempo')
ylabel('Temperatura')
legend('-DynamicLegend','location','southwest')
grid on
hold off