Simetría axial

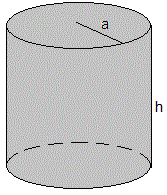
Resolveremos dos problemas que tiene simetría alrededor del eje Z y por tanto, es independiente del ángulo φ

Estudiaremos la distribución de temperaturas en el estado estacionario de un cilindro sólido de radio a y altura h cuando se especifica:

• La temperatura en la base inferior, T(ρ,0)
• La temperatura en la base superior, T(ρ, h)
• La temperatura en la superficie lateral, T(a, z)

La ecuación de Laplace en coordenadas cilíndricas

${\displaystyle \frac{1}{\rho }\frac{\partial }{\partial \rho }\left(\rho \frac{\partial T}{\partial \rho }\right)+\frac{{\partial }^{2}T}{\partial z^2}=0}$

que resolvemos por el método de separación de variables T(ρ,z)=R(ρ)·Z(z)

${\displaystyle Z(z)\frac{1}{\rho }\frac{d}{d\rho }\left(\rho \frac{dR}{d\rho }\right)+R(\rho )\frac{d^{2}Z}{d{z}^2}=0}$

Primer problema

La ecuación diferencial en derivadas parciales da lugar a un sistema de dos ecuaciones diferenciales. En esta ocasión, elegimos la igualdad a -k²,

${\displaystyle \frac{1}{R}\frac{1}{\rho }\frac{d}{d\rho }\left(\rho \frac{dR}{d\rho }\right)=-\frac{1}{Z}\frac{d^{2}z}{d{z}^2}=-k^2,\{\begin{array}{l}\frac{d^{2}R}{d{\rho }^2}+\frac{1}{\rho }\frac{dR}{d\rho }+k^{2}R=0\\ \frac{d^{2}Z}{d{z}^2}-k^{2}Z=0\end{array}}$

La primera ecuación diferencial se escribe

${\displaystyle {\rho }^2\frac{d^{2}R}{d{\rho }^2}+\rho \frac{dR}{d\rho }+k^2{\rho }^{2}R=0}$

Haciendo el cambio de variable x=kρ

${\displaystyle x^2\frac{d^{2}R}{d{x}^2}+x\frac{dR}{dx}+x^{2}R=0}$

Que es la ecuación diferencial de Bessel con n=0. Las soluciones de las dos ecuaciones diferenciales son

${\displaystyle \begin{array}{l}R(\rho )=A{J}_0\left(k\rho \right)+B{Y}_0\left(k\rho \right)\\ Z(z)=C\exp \left(-kz\right)+D\exp \left(kz\right)\end{array}}$

Se descarta el término Y₀(kρ) ya que cuando ρ→0, Y₀(kρ)→∞. Por tanto, el coeficiente B=0

Las condiciones de contorno son

${\displaystyle \{\begin{array}{l}T(\rho \mathrm{,0})=100\\ T(a,z)=0\\ T(\rho ,h)=0\end{array}}$

La condición de contorno en la superficie del cilindro, T(a, z)=0, hace que

${\displaystyle A{J}_0(ka)\left(C\exp (-kz)+D\exp (kz)\right)=0}$

α_n=ka son las raíces de la ecuación transcendente J₀(ka)=0

La solución de la ecuación de Laplace es la superposición

${\displaystyle T(\rho ,z)={\displaystyle \sum _{n=1}^{\infty }{J}_0\left({\alpha }_n\frac{\rho }{a}\right)}\left(C_n\exp \left(-\frac{{\alpha }_n}{a}z\right)+D_n\exp \left(\frac{{\alpha }_n}{a}z\right)\right)}$

Las condiciones de contorno en las bases inferior y superior T(ρ,0) y T(ρ, h) nos permiten calcular los coeficientes C_n y D_n. Utilizamos las relaciones de ortogonalidad de las funciones J(x) de Bessel para calcularlos

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{1}{\int }}x{J}_0({\alpha }_{m}x)J_0({\alpha }_{n}x)dx}=0m\ne n\\ {\displaystyle \underset{0}{\overset{1}{\int }}x{J}_0^2({\alpha }_{n}x)dx}=\frac{1}{2}{J}_1^2({\alpha }_n)\end{array}}$

donde α_m y α_n son raíces distintas de J₀(ka)=0 y x=ρ/a

1. La primera ecuación es

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{1}{\int }}xT(\rho \mathrm{,0})J_0\left({\alpha }_{m}x\right)dx}={\displaystyle \underset{0}{\overset{1}{\int }}\left({\displaystyle \sum _{n=1}^{\infty }{J}_0\left({\alpha }_{n}x\right)}\left(C_n+D_n\right)\right)x·J_0\left({\alpha }_{m}x\right)dx}\\ {\displaystyle \underset{0}{\overset{1}{\int }}xT(\rho \mathrm{,0})J_0\left({\alpha }_{m}x\right)dx}=\left(C_n+D_n\right){\displaystyle \sum _{n=1}^{\infty }{\displaystyle \underset{0}{\overset{1}{\int }}\left(x·J_0\left({\alpha }_{m}x\right)J_0\left({\alpha }_{n}x\right)\right)dx}}\\ {\displaystyle \underset{0}{\overset{1}{\int }}xT(\rho \mathrm{,0})J_0\left({\alpha }_{n}x\right)dx}=\left(C_n+D_n\right)\frac{1}{2}{J}_1^2({\alpha }_n)\end{array}}$

Si T(ρ,0)=100. Utilizamos la relación

${\displaystyle {\displaystyle \underset{0}{\overset{1}{\int }}x{J}_0({\alpha }_{n}x)dx}=\frac{1}{{\alpha }_n}{J}_1({\alpha }_n)}$

El resultado es

${\displaystyle \frac{100}{{\alpha }_n}=\frac{1}{2}\left(C_n+D_n\right)J_1({\alpha }_n)}$

2. La segunda ecuación es

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{1}{\int }}xT(\rho ,h)J_0\left({\alpha }_{m}x\right)dx}={\displaystyle \underset{0}{\overset{1}{\int }}{\displaystyle \sum _{n=1}^{\infty }{J}_0\left({\alpha }_{n}x\right)}\left(C_n\exp \left(-{\alpha }_n\frac{z}{a}\right)+D_n\exp \left({\alpha }_n\frac{z}{a}\right)\right)x·J_0\left({\alpha }_{m}x\right)dx}\\ {\displaystyle \underset{0}{\overset{1}{\int }}xT(\rho ,h)J_0\left({\alpha }_{m}x\right)dx}={\displaystyle \sum _{n=1}^{\infty }\left(C_n\exp \left(-{\alpha }_n\frac{z}{a}\right)+D_n\exp \left({\alpha }_n\frac{z}{a}\right)\right)}{\displaystyle \underset{0}{\overset{1}{\int }}x{J}_0\left({\alpha }_{m}x\right)J_0\left({\alpha }_{n}x\right)dx}\\ {\displaystyle \underset{0}{\overset{1}{\int }}xT(\rho ,h)J_0\left({\alpha }_{m}x\right)dx}=\left(C_n\exp \left(-{\alpha }_n\frac{h}{a}\right)+D_n\exp \left({\alpha }_n\frac{h}{a}\right)\right)\frac{1}{2}{J}_1^2({\alpha }_n)\end{array}}$

Si T(ρ, h)=0.

${\displaystyle C_n\exp \left(-{\alpha }_n\frac{h}{a}\right)+D_n\exp \left({\alpha }_n\frac{h}{a}\right)=0}$

Despejamos C_n y D_n del sistema de dos ecuaciones

${\displaystyle \begin{array}{l}{C}_n=\frac{200}{{\alpha }_n{J}_1({\alpha }_n)}\frac{\exp \left({\alpha }_n\frac{h}{a}\right)}{\exp \left({\alpha }_n\frac{h}{a}\right)-\exp \left(-{\alpha }_n\frac{h}{a}\right)}=\frac{100}{{\alpha }_n{J}_1({\alpha }_n)}\frac{\exp \left({\alpha }_n\frac{h}{a}\right)}{\sinh \left({\alpha }_n\frac{h}{a}\right)}\\ D_n=-\frac{100}{{\alpha }_n{J}_1({\alpha }_n)}\frac{\exp \left(-{\alpha }_n\frac{h}{a}\right)}{\sinh \left({\alpha }_n\frac{h}{a}\right)}\end{array}}$

La distribución de temperaturas con simetría axial es

${\displaystyle T(\rho ,z)=200{\displaystyle \sum _{n=1}^{\infty }\frac{J_0\left({\alpha }_n\frac{\rho }{a}\right)\sinh \left({\alpha }_n\frac{h-z}{a}\right)}{{\alpha }_n{J}_1\left({\alpha }_n\right)\sinh \left({\alpha }_n\frac{h}{a}\right)}}}$

Definimos la función que calcula la temperatura T(ρ, z) tomando los N raíces de la ecuación transcendente J₀(ka)=0

function T = laplace_temperatura_2(x, z, alfa, a, h)
    T=0;
    for n=1:length(alfa)
        T=T+besselj(0,alfa(n)*x/a).*sinh(alfa(n)*(h-z)/a)/
(alfa(n)*sinh(alfa(n)*h/a)*besselj(1,alfa(n)));
    end
    T=T*200;
end

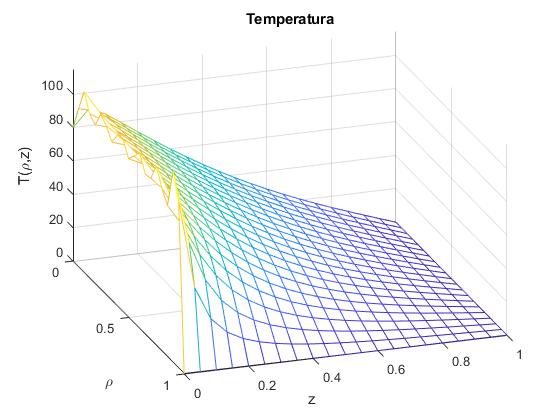
Creamos un script para representar la temperatura T(ρ, z) en el recinto 0≤ρ≤a e 0≤z≤h, con a=1 y h=1. Se han tomado length(alfa)=12 términos del desarrollo en serie

Utilizamos la función raices para calcular las raíces múltiples de una función, véase la página titulada Funciones MATLAB para calcular las raíces de una ecuación

x=linspace(0,40,40);
alfa=raices(@(x) besselj(0,x),x); %raíces

a=1; %radio cilindro
h=1; %altura
[x,z] = meshgrid(0:0.05:a, 0:0.05:h);
T=laplace_temperatura2(x, z, alfa, a, h); %T(x,y)
mesh(x,z,T)
xlabel('\rho')
ylabel('z')
zlabel('T(\rho,z)')
title('Temperatura')
view(71,32)

Segundo problema

La ecuación diferencial en derivadas parciales da lugar a un sistema de dos ecuaciones diferenciales. En esta ocasión, elegimos la igualdad a k²,

${\displaystyle \frac{1}{R}\frac{1}{\rho }\frac{d}{d\rho }\left(\rho \frac{dR}{d\rho }\right)=-\frac{1}{Z}\frac{d^{2}z}{d{z}^2}=k^2,\{\begin{array}{l}\frac{d^{2}R}{d{\rho }^2}+\frac{1}{\rho }\frac{dR}{d\rho }-k^{2}R=0\\ \frac{d^{2}Z}{d{z}^2}+k^{2}Z=0\end{array}}$

La primera ecuación diferencial se escribe

${\displaystyle {\rho }^2\frac{d^{2}R}{d{\rho }^2}+\rho \frac{dR}{d\rho }-k^2{\rho }^{2}R=0}$

Haciendo el cambio de variable x=kρ

${\displaystyle x^2\frac{d^{2}R}{d{x}^2}+x\frac{dR}{dx}-x^{2}R=0}$

Que es la ecuación diferencial modificada de Bessel con n=0. Las soluciones de las dos ecuaciones diferenciales son

${\displaystyle \begin{array}{l}R(\rho )=A{I}_0\left(k\rho \right)+B{K}_0\left(k\rho \right)\\ Z(z)=C\cos \left(-kz\right)+D\sin \left(kz\right)\end{array}}$

Se descarta el término K₀(ρ) ya que cuando ρ→0, K₀(ρ)→∞, lo que implica que B=0

Las condiciones de contorno

${\displaystyle \{\begin{array}{l}T(\rho \mathrm{,0})=0\\ T(\rho ,h)=0\\ T(a,z)=100\end{array}}$

La condición de contorno en la base inferior del cilindro T(ρ, 0)=0 implica que C=0.

La condición de contorno en la base superior del cilindro T(ρ, h)=0 implica que sin(kh)=0, kh=nπ, (n=1,2,3...)

La solución de la ecuación de Laplace es la superposición

${\displaystyle T(\rho ,z)={\displaystyle \sum _{n=1}^{\infty }{D}_n{I}_0\left(\frac{n\pi }{h}\rho \right)}\sin \left(\frac{n\pi }{h}z\right)}$

Las condición de contorno en la superficie lateral T(a, z) nos permite calcular el coeficiente D_n

${\displaystyle T(a,z)={\displaystyle \sum _{n=1}^{\infty }{D}_n{I}_0\left(\frac{n\pi }{h}a\right)}\sin \left(\frac{n\pi }{h}z\right)}$

Utilizamos el procedimiento para calcular los coeficientes del desarrollo en serie de Fourier de una función periódica

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{h}{\int }}T(a,z)}\sin \left(\frac{m\pi }{h}z\right)dz={\displaystyle \underset{0}{\overset{h}{\int }}\left\{{\displaystyle \sum _{n=1}^{\infty }{D}_n{I}_0\left(\frac{n\pi }{h}a\right)}\sin \left(\frac{n\pi }{h}z\right)\right\}\sin \left(\frac{m\pi }{h}z\right)dz}\\ {\displaystyle \underset{0}{\overset{h}{\int }}T(a,z)}\sin \left(\frac{m\pi }{h}z\right)dz={\displaystyle \sum _{n=1}^{\infty }{D}_n{I}_0\left(\frac{n\pi }{h}a\right)}{\displaystyle \underset{0}{\overset{h}{\int }}\sin \left(\frac{n\pi }{h}z\right)\sin \left(\frac{m\pi }{h}z\right)dz}\\ {\displaystyle \underset{0}{\overset{h}{\int }}T(a,z)}\sin \left(\frac{n\pi }{h}z\right)dz=D_n{I}_0\left(\frac{n\pi }{h}a\right)\frac{h}{2}\end{array}}$

>> syms x h m n;
>> assume(m,'integer')
>> assume(n,'integer')
>> res=int(sin(n*pi*x/h)*sin(m*pi*x/h),x,0,h);
>> simplify(res)
ans =0

>> res=int(sin(n*pi*x/h)^2,x,0,h);
>> simplify(res)
ans =h/2

Si la temperatura en la superficie lateral T(a, z)=100

${\displaystyle \begin{array}{l}\frac{h}{n\pi }100\left(1-\cos (n\pi )\right)=D_n{I}_0\left(\frac{n\pi }{h}a\right)\frac{h}{2}\\ D_n=\frac{400}{n\pi I_0\left(\frac{n\pi }{h}a\right)},n=\mathrm{1,3,5...}\end{array}}$

La distribución de temperaturas con simetría axial es

${\displaystyle T(\rho ,z)=\frac{400}{\pi }{\displaystyle \sum _{n=\mathrm{1,3,5...}}^{\infty }\frac{1}{n}\frac{I_0\left(\frac{n\pi }{h}\rho \right)}{I_0\left(\frac{n\pi }{h}a\right)}}\sin \left(\frac{n\pi }{h}z\right)}$

Definimos la función que calcula la temperatura T(ρ, z) tomado N=10 términos del desarrollo en serie

function T = laplace_temperatura_3(x, z, a, h)
    T=0;
    for n=1:2:20
        T=T+besseli(0,n*x/h).*sin(n*pi*z/h)/(n*besseli(0,n*pi*a/h));
    end
    T=T*400/pi;
end

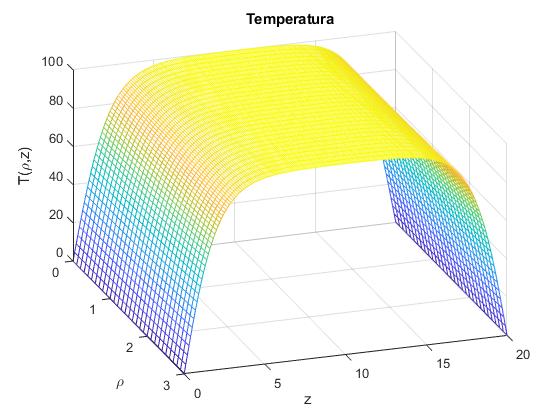
Creamos un script para representar la temperatura T(ρ, z) en el recinto 0≤ρ≤a e 0≤z≤h, con a=3 y h=20.

a=3; %radio del cilindro
h=20; %altura
[x,z] = meshgrid(0:0.1:a, 0:0.1:h);
T=laplace_temperatura_3(x, z, a, h); %T(x,y)
mesh(x,z,T)
xlabel('\rho')
ylabel('z')
zlabel('T(\rho,z)')
title('Temperatura')
view(71,32)

Distribución de temperaturas en un disco en el estado estacionario

La ecuación de la conducción del calor en el estado estacionario, independiente del tiempo, es la ecuación de Laplace en coordenadas cilíndricas.

${\displaystyle \frac{1}{\rho }\frac{\partial }{\partial \rho }\left(\rho \frac{\partial T}{\partial \rho }\right)+\frac{1}{{\rho }^2}\frac{{\partial }^{2}T}{\partial {\phi }^2}=0}$

La solución se escribe como producto de dos funciones una R(ρ) que depende solamente de ρ y otra F(φ), que depende solamente de φ. T(ρ,φ)=R(ρ)·F(φ)

${\displaystyle \begin{array}{l}F(\phi )\frac{1}{\rho }\frac{d}{d\rho }\left(\rho \frac{dR(\rho )}{d\rho }\right)+R(\rho )\frac{1}{{\rho }^2}\frac{d^{2}F(\phi )}{d{\phi }^2}=0\hfill \\ \frac{\rho }{R(\rho )}\frac{d}{d\rho }\left(\rho \frac{dR(\rho )}{d\rho }\right)=-\frac{1}{F(\phi )}\frac{d^{2}F(\phi )}{d{\phi }^2}=k^2\hfill \end{array}}$

Esto da lugar a dos ecuaciones diferenciales,

${\displaystyle \begin{array}{l}{\rho }^2\frac{d^{2}R}{d{\rho }^2}+\rho \frac{dR}{d\rho }-k^{2}R=0\\ \frac{d^{2}F}{d{\phi }^2}+k^{2}F=0\end{array}}$

Solución F(φ)

La solución de la segunda ecuación diferencial es sencilla

${\displaystyle F(\phi )=\{\begin{array}{l}A\cos (k\phi )+B\sin (k\phi ),k\ne 0\\ a_0\phi +b_0,k=0\end{array}}$

F(φ)=F(φ+2π) tiene que ser una función periódica

• Para k≠0, implica

${\displaystyle \begin{array}{l}A\cos (k\phi )+B\sin (k\phi )=A\cos \left(k(\phi +2\pi )\right)+B\sin \left(k(\phi +2\pi )\right)\\ \sin \left(\alpha +k\phi \right)=\sin \left(\alpha +k(\phi +2\pi )\right),\tan \alpha =\frac{A}{B}\end{array}}$

Aplicando la fórmula de la diferencia de senos, sin(a+b)-sin(a-b)=2sinb·cosa

${\displaystyle \begin{array}{l}\{\begin{array}{l}a+b=\alpha +k(\phi +2\pi )\\ a-b=\alpha +k\phi \end{array}\{\begin{array}{l}a=\alpha +k(\phi +\pi )\\ b=k\pi \end{array}\\ \sin \left(k\pi \right)\cos \left(\alpha +k(\phi +\pi )\right)=\mathrm{0,}k=n,\text{entero}\end{array}}$

• Para k=0, implica que a₀=0

Solución R(r)

• Para k≠0, hacemos la sustitución ρ=e^x, x=lnρ, quedando una ecuación diferencial de coeficientes constantes, cuya solución es inmediata

${\displaystyle \begin{array}{l}\frac{dR}{d\rho }=\frac{dR}{dx}\frac{dx}{d\rho }=\frac{dR}{dx}\frac{1}{\rho }=\frac{dR}{dx}{e}^{-x}\\ \frac{d^{2}R}{d{\rho }^2}=\frac{d}{d\rho }\left(\frac{dR}{d\rho }\right)=\frac{d}{dx}\left(\frac{dR}{d\rho }\right)\frac{dx}{d\rho }=\frac{d}{dx}\left(\frac{dR}{dx}{e}^{-x}\right)\frac{dx}{d\rho }=e^{-2x}\frac{d^{2}R}{d{x}^2}-e^{-2x}\frac{dR}{dx}\\ {\rho }^2\frac{d^{2}R}{d{\rho }^2}+\rho \frac{dR}{d\rho }-k^{2}R=0\\ e^{2x}\left(e^{-2x}\frac{d^{2}R}{d{x}^2}-e^{-2x}\frac{dR}{dx}\right)+e^x\left(\frac{dR}{dx}{e}^{-x}\right)-k^{2}R=0\\ \frac{d^{2}R}{d{x}^2}-k^{2}R=0\\ R=C{e}^{-kx}+D{e}^{kx}=C{\rho }^{-k}+D{\rho }^k\end{array}}$

• Cuando k=0, la solución de la primera ecuación diferencial es

${\displaystyle \begin{array}{l}\frac{d}{d\rho }\left(\rho \frac{dR}{d\rho }\right)=0\\ \frac{dR}{d\rho }=\frac{C}{\rho }\\ R(\rho )=C\ln \rho +D\end{array}}$

La solución, T(ρ,φ)=R(ρ)·F(φ), es el producto de

${\displaystyle F(\phi )=\{\begin{array}{l}A\cos (k\phi )+B\sin (k\phi )\\ b_0\end{array}R(\rho )=\{\begin{array}{l}C{\rho }^{-k}+D{\rho }^k,k>0\\ c_0\ln \rho +d_0,k=0\end{array}}$

Se descarta los términos ρ^-k y lnρ, que se hacen infinito cuando ρ→0. La solución de la ecuación de Laplace es la superposición

${\displaystyle T(\rho ,\phi )=A_0+{\displaystyle \sum _{n=1}^{\infty }{\rho }^n}\left(A_n\cos (n\phi )+B_n\sin (n\phi )\right)}$

Primer problema

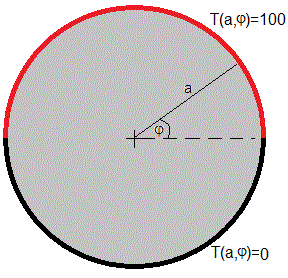
Supongamos un cilindro muy largo, la mitad de la superficie lateral se mantiene a 100 grados y la otra mitad se mentiene a 0 grados

${\displaystyle \{\begin{array}{l}T(a,\phi )=\mathrm{100,}0\le \phi <\pi \\ T(a,\phi )=\mathrm{0,}\pi \le \phi <2\pi \end{array}}$

La distribución de temperaturas no depende de z solamente de la distancia radial ρ y del ángulo φ

Calculamos los coeficientes A_n y B_n a partir de las condiciones de contorno

• Coeficientes B_n

${\displaystyle \begin{array}{l}T(a,\phi )=A_0+{\displaystyle \sum _{n=1}^{\infty }{a}^n\left(A_n\cos (n\phi )+B_n\sin (n\phi )\right)}\\ {\displaystyle \underset{0}{\overset{2\pi }{\int }}T(a,\phi )\sin (m\phi )d\phi ={\displaystyle \underset{0}{\overset{2\pi }{\int }}{A}_0\sin (m\phi )d\phi +{\displaystyle \underset{0}{\overset{2\pi }{\int }}\left\{{\displaystyle \sum _{n=1}^{\infty }{a}^n\left(A_n\cos (n\phi )+B_n\sin (n\phi )\right)}\right\}}}}\sin (m\phi )d\phi \\ {\displaystyle \underset{0}{\overset{2\pi }{\int }}T(a,\phi )\sin (m\phi )d\phi ={\displaystyle \underset{0}{\overset{2\pi }{\int }}{A}_0\sin (m\phi )d\phi +{\displaystyle \sum _{n=1}^{\infty }{a}^n\left(A_n{\displaystyle \underset{0}{\overset{2\pi }{\int }}\sin (m\phi )}\cos (n\phi )d\phi +B_n{\displaystyle \underset{0}{\overset{2\pi }{\int }}\sin (m\phi )}\sin (n\phi )d\phi \right)}}}\\ 100{\displaystyle \underset{0}{\overset{\pi }{\int }}\sin (n\phi )d\phi }=a^n\pi B_n\\ B_n=\frac{200}{a^n\pi n},n=\mathrm{1,3,5...}\end{array}}$

>> syms x m n;
>> assume(m,'integer')
>> assume(n,'integer')
>>z= int(sin(m*x)*cos(n*x),x,0,2*pi); 
>> simplify(z) 
ans =0
>> z= int(sin(n*x)*cos(n*x),x,0,2*pi);
>> simplify(z)
ans =0

>> z= int(sin(m*x)*sin(n*x),x,0,2*pi);
>> simplify(z)
ans =0
>>z= int(sin(m*x)^2,x,0,2*pi);
>> simplify(z)
 ans =pi

• Coeficientes A_n

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{2\pi }{\int }}T(a,\phi )\cos (m\phi )d\phi ={\displaystyle \underset{0}{\overset{2\pi }{\int }}{A}_0\cos (m\phi )d\phi +{\displaystyle \sum _{n=1}^{\infty }{a}^n\left(A_n{\displaystyle \underset{0}{\overset{2\pi }{\int }}\cos (m\phi )}\cos (n\phi )d\phi +B_n{\displaystyle \underset{0}{\overset{2\pi }{\int }}\cos (m\phi )}\sin (n\phi )d\phi \right)}}}\\ 100{\displaystyle \underset{0}{\overset{\pi }{\int }}\cos (n\phi )d\phi }=a^n\pi A_n\\ A_n=0\end{array}}$

>> z= int(cos(m*x)^2,x,0,2*pi);
>> simplify(z)
ans =pi

>> z= int(cos(m*x)*sin(n*x),x,0,2*pi);
>> simplify(z)
ans =0
>> z= int(cos(n*x)*sin(n*x),x,0,2*pi);
>> simplify(z) 
ans =0

MATLAB no da una respuesta única a la integral

${\displaystyle {\displaystyle \underset{0}{\overset{2\pi }{\int }}\cos (m\phi )}\cos (n\phi )d\phi =\mathrm{0,}m\ne n}$

• Se calcula el coeficiente A₀, sabiendo que la temperatura del punto T(a,π/2)=100

${\displaystyle T\left(a,\frac{\pi }{2}\right)=A_0+\frac{200}{\pi }{\displaystyle \sum _{n=\mathrm{1,3,5..}}^{\infty }\frac{1}{n}\sin \left(n\frac{\pi }{2}\right)}}$

La serie vale π/4, A₀=50

>> syms x;
>> z=symsum(sin((2*x-1)*pi/2)/(2*x-1),x,1,inf);
>> simplify(z)
ans =pi/4

La distribución de temperaturas en el disco es

${\displaystyle T(\rho ,\phi )=50+\frac{200}{\pi }{\displaystyle \sum _{n=\mathrm{1,3,5...}}^{\infty }{\left(\frac{\rho }{a}\right)}^n\frac{\sin (n\phi )}{n}}}$

Definimos la función que calcula la temperatura T(ρ, φ) tomado N=50 términos del desarrollo en serie

function T = laplace_temperatura_4(r, phi, a)
    T=0;
    for n=1:2:100
        T=T+((r/a).^n).*sin(n*phi)/n;
    end
    T=50+T*200/pi;
end

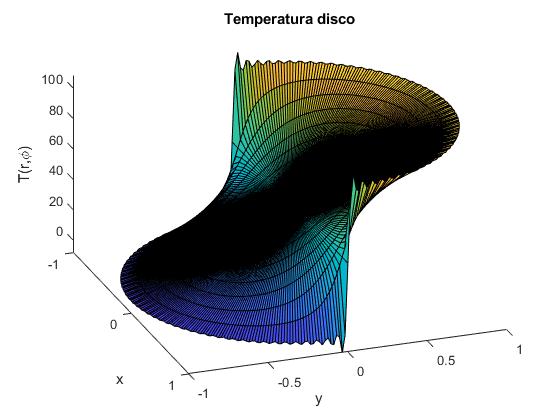
Creamos un script para representar la temperatura T(ρ, φ) con a=1.

a=1; %radio disco
r=0:0.1:1;
phi=0:pi/180:2*pi;
[r,phi]=meshgrid(r,phi);
x=r.*cos(phi);
y=r.*sin(phi);
z=laplace_temperatura_4(r, phi, a);
hold on
surf(x,y,z)
xlabel('x')
ylabel('y')
zlabel('T(r,\phi)')
title('Temperatura disco')
view(70,36)

Segundo problema

La función T(a,φ)=f(φ), 0≤φ<2π, describe la temperartura fija en el bode del disco, lo que nos permitirá calcular los coeficientes A₀, A₁,...A_n, B₁,...B_n,

${\displaystyle T(a,\phi )=A_0+{\displaystyle \sum _{n=1}^{\infty }{a}^n}\left(A_n\cos (n\phi )+B_n\sin (n\phi )\right)}$

Teniendo en cuenta las relaciones

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{2\pi }{\int }}\cos (n}x)\cos (mx)dx=\mathrm{0,}m\ne n\\ {\displaystyle \underset{0}{\overset{2\pi }{\int }}\sin (n}x)\sin (mx)dx=\mathrm{0,}m\ne n\end{array}}$

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{2\pi }{\int }}\sin (n}x)dx=\mathrm{0,}{\displaystyle \underset{0}{\overset{2\pi }{\int }}\cos (n}x)dx=0\\ {\displaystyle \underset{0}{\overset{2\pi }{\int }}{\sin }^2(n}x)dx=\pi ,{\displaystyle \underset{0}{\overset{2\pi }{\int }}{\cos }^2(n}x)dx=\pi \end{array}}$

>> syms t m n;
>> assume(n,'integer');
>> assume(m,'integer');
>> int(sin(n*t),t,0,2*pi)
>> simplify(ans)
ans =0
>> int(cos(n*t),t,0,2*pi)
ans =0
>> int(cos(n*t)^2,t,0,2*pi)
>> simplify(ans)
ans =pi
>> int(sin(n*t)^2,t,0,2*pi)
>> simplify(ans)
ans =pi

Los coeficientes valen

${\displaystyle \begin{array}{l}{A}_0=\frac{1}{2\pi }{\displaystyle \underset{0}{\overset{2\pi }{\int }}f(\phi )d\phi }\\ A_n=\frac{1}{\pi a^n}{\displaystyle \underset{0}{\overset{2\pi }{\int }}f(\phi )\cos (n\phi )d\phi }\\ B_n=\frac{1}{\pi a^n}{\displaystyle \underset{0}{\overset{2\pi }{\int }}f(\phi )\sin (n\phi )d\phi }\end{array}}$

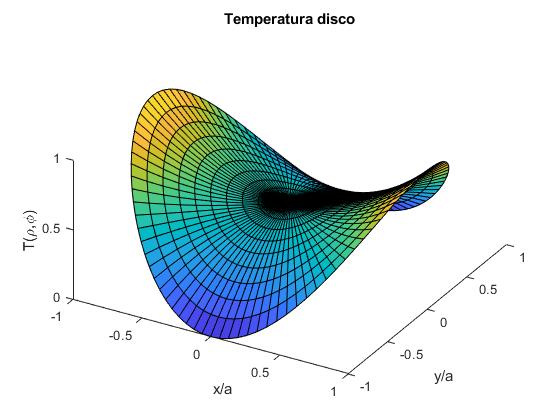
Ejemplo

La temperatura fija en el bode del disco viene descrita por la función f(φ)=cos²φ=(1+cos(2φ))/2. Los coeficientes no nulos son

${\displaystyle \begin{array}{l}{A}_0=\frac{1}{2\pi }\frac{1}{2}{\displaystyle \underset{0}{\overset{2\pi }{\int }}\left(1+\cos (2\phi )\right)d\phi }=\frac{1}{2}\\ A_2=\frac{1}{\pi a^2}\frac{1}{2}{\displaystyle \underset{0}{\overset{2\pi }{\int }}\left(1+\cos (2\phi )\right)\cos (2\phi )d\phi }=\frac{1}{2a^2}\end{array}}$

La temperarura en el disco en el estado estacionario es

${\displaystyle T(\rho ,\phi )=\frac{1}{2}+\frac{1}{2}\frac{{\rho }^2}{a^2}\cos (2\phi )}$

r=0:0.1:1;
phi=0:pi/50:2*pi;
[r,phi]=meshgrid(r,phi);
x=r.*cos(phi);
y=r.*sin(phi);
z=1/2+(r.^2).*cos(2*phi)/2;
hold on
surf(x,y,z)
xlabel('x/a')
ylabel('y/a')
zlabel('T(\rho,\phi)')
title('Temperatura disco')
view(30,47)

Referencias

Physics 116C Home Page---Fall 2011, VI. Solutions to Homework Problem Sets and Exams. Problems 1, 3, 4