Vamos a estudiar dos situaciones en coordendas rectangulares

Recinto semiinfinito

Resolveremos la ecuación de Laplace en coordenadas rectangulares por el procedimiento de separación de variables

${\displaystyle \frac{\partial T}{\partial x^2}+\frac{\partial T}{\partial y^2}=0}$

Sea T(x,y)=X(x)·Y(y), la temperatura en un punto (x,y) de un recinto rectangular. La ecuación diferencial en derivadas parciales da lugar a un sistema de dos ecuaciones diferenciales. Elegimos que sea oscilatoria a lo largo del eje X y exponencial a lo largo del eje Y

${\displaystyle \begin{array}{l}Y(y)\frac{d^{2}X}{d{x}^2}=-X(x)\frac{d^{2}Y}{d{y}^2}\\ \frac{1}{X}\frac{d^{2}X}{d{x}^2}=-\frac{1}{Y}\frac{d^{2}Y}{d{y}^2}=-k^2,\{\begin{array}{l}\frac{d^{2}X}{d{x}^2}+k^{2}X=0\\ \frac{d^{2}Y}{d{x}^2}-k^{2}Y=0\end{array}\end{array}}$

La solución de cada una de las dos ecuaciones diferenciales es conocida

${\displaystyle \begin{array}{l}X(x)=A\cos (kx)+B\sin (kx)\\ Y(y)=C\exp (-ky)+D\exp (ky)\end{array}}$

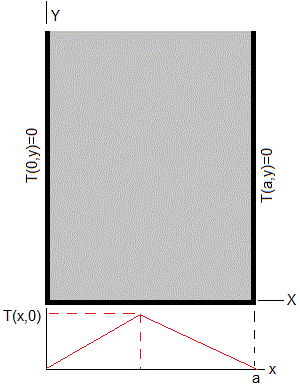
Sea un recinto semiinfinto de anchura a. Las condiciones de contorno son la siguientes:

${\displaystyle \begin{array}{l}T(\mathrm{0,}y)=0\\ T(a,y)=0\\ T(x\mathrm{,0})=\{\begin{array}{l}x,0<x<\frac{a}{2}\\ a-x,\frac{a}{2}\le x<a\end{array}\end{array}}$

Como T(x,y)→0 cuando y→∞ el coeficiente D=0, tiene que ser nulo, para que la solución esté acotada.

Como T(0, y)=0, el coeficiente A tiene que ser nulo

Como T(a, y)=0, se tendrá que cumplir que sin(ka)=0, k=nπ/a (n=1,2.3...). En consecuencia

${\displaystyle X(x)=B\sin \left(\frac{n\pi }{a}x\right)}$

La solución de la ecuación de Laplace con las condiciones de contorno especificadas es la superposición

${\displaystyle T(x,y)={\displaystyle \sum _{n=1}^{\infty }\left(B_n\sin \left(\frac{n\pi }{a}x\right)\right)}\left(C_n\exp \left(-\frac{n\pi }{a}y\right)\right)={\displaystyle \sum _{n=1}^{\infty }{A}_n\sin \left(\frac{n\pi }{a}x\right)\exp \left(-\frac{n\pi }{a}y\right)}}$

La condición de contorno T(x, 0) determina los coeficientes A_n

${\displaystyle T(x\mathrm{,0})={\displaystyle \sum _{n=1}^{\infty }{A}_n\sin \left(\frac{n\pi }{a}x\right)}}$

Utilizamos el procedimiento para calcular los coeficientes del desarrollo en serie de Fourier de una función periódica

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{a}{\int }}T(x\mathrm{,0})\sin \left(\frac{m\pi }{a}x\right)dx}={\displaystyle \underset{0}{\overset{a}{\int }}\left({\displaystyle \sum _{n=1}^{\infty }{A}_n\sin \left(\frac{n\pi }{a}x\right)}\right)\sin \left(\frac{m\pi }{a}x\right)dx}\\ {\displaystyle \underset{0}{\overset{a}{\int }}T(x\mathrm{,0})\sin \left(\frac{m\pi }{a}x\right)dx}={\displaystyle \sum _{n=1}^{\infty }{A}_n{\displaystyle \underset{0}{\overset{a}{\int }}\sin \left(\frac{n\pi }{a}x\right)\sin \left(\frac{m\pi }{a}x\right)dx}}\end{array}}$

>> syms x a m n;
>> assume(n,'integer');
>> assume(m,'integer');
>> z=int(sin(m*pi*x/a)*sin(n*pi*x/a),x,0,a);
>> simplify(z) 
ans =0
 
>> z=int(sin(m*pi*x/a)^2,x,0,a);
>> simplify(z)
ans =a/2

La integral es distinta de cero cuando m=n

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{a}{\int }}T(x\mathrm{,0})\sin \left(\frac{n\pi }{a}x\right)dx}=A_n\frac{a}{2}\\ A_n\frac{a}{2}={\displaystyle \underset{0}{\overset{a/2}{\int }}x}\sin \left(\frac{n\pi }{a}x\right)dx+{\displaystyle \underset{a/2}{\overset{a}{\int }}(a-x)}\sin \left(\frac{n\pi }{a}x\right)dx\\ A_n\frac{a}{2}=2\frac{a^2}{n^2{\pi }^2}\sin \left(\frac{n\pi }{2}\right)\\ A_n=\frac{4a}{n^2{\pi }^2}\sin \left(\frac{n\pi }{2}\right),\{\begin{array}{l}{A}_n=\mathrm{0,}n=2m\\ A_n={\left(-1\right)}^m,n=2m+1\end{array}\end{array}}$

La función T(x, 0) se aproxima mediante la serie

${\displaystyle T(x\mathrm{,0})=\frac{4a}{{\pi }^2}{\displaystyle \sum _{m=0}^{\infty }\frac{{(-1)}^m}{{\left(2m+1\right)}^2}\sin \left(\frac{(2m+1)\pi }{a}x\right)}}$

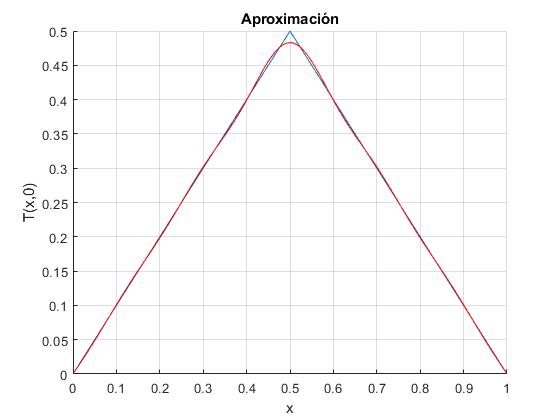
Ejemplo. Sea a=1. Tomemos los cinco primeros términos del desarrollo en serie de Fourier

a=1;
hold on
line([0,a/2],[0,a/2])
line([a/2,a],[a/2,0])
x=linspace(0,a,100);
z=0;
for m=0:5
    z=z+(-1)^m*sin((2*m+1)*pi*x/a)/(2*m+1)^2;
end
z=z*4*a/pi^2;
plot(x,z, 'r')
hold off
xlabel('x')
zlabel('T(x,0)')
grid on
title('Aproximación')

La temperatura T(x,y) en cualquier punto (x,y) del recinto rectangular es

${\displaystyle T(x,y)=\frac{4a}{{\pi }^2}{\displaystyle \sum _{m=0}^{\infty }\frac{{(-1)}^m}{{\left(2m+1\right)}^2}\sin \left(\frac{(2m+1)\pi }{a}x\right)\exp \left(-\frac{(2m+1)\pi }{a}y\right)}}$

Definimos la función que calcula la temperatura T(x,y) tomando los N primeros términos del desarrollo en serie

function z = laplace_temperatura(x,y, N, a)
    z=0;
    for m=0:N
        z=z+(-1)^m*sin((2*m+1)*pi*x/a).*exp(-(2*m+1)*pi*y/a)/(2*m+1)^2;
    end
    z=z*4*a/pi^2;
end

Creamos un script para representar la temperatura T(x,y) en el recinto rectangular 0≤x≤a e 0≤y≤1, con a=1. Se han tomado N=20 términos del desarrollo en serie

a=1; %anchura
N=20; %número de términos
[x,y] = meshgrid(0:0.02:a, 0:0.02:1);
z=laplace_temperatura(x,y, N, a); %T(x,y)
mesh(x,y,z)
xlabel('x')
ylabel('y')
zlabel('T(x,y)')
title('Temperatura')
view(47,32)

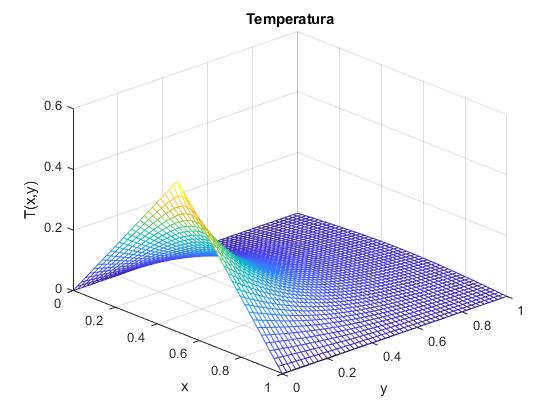
La temperatura disminuye rápidamente cuando nos alejamos del eje X

Recinto rectangular

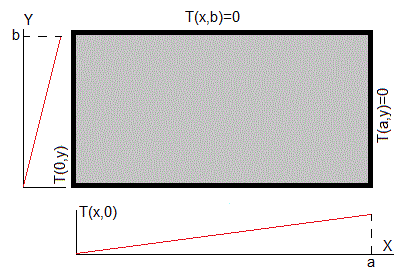
Sea un recinto rectangular de dimensiones a y b. Vamos a cualcular la temperatura T(x,y) en un punto (x,y) de dicho recinto rectangular con las siguienets condiciones de contorno

${\displaystyle \{\begin{array}{l}T(x\mathrm{,0})=x\\ T(x,b)=0\end{array}\{\begin{array}{l}T(\mathrm{0,}y)=y\\ T(a,y)=0\end{array}}$

La temperatura en un punto (x,y) del rectángulo de dimensiones a y b es la suma de dos contribuciones, T(x,y)=T₁(x,y)+T₂(x,y)

Primer sumando

La solución de la ecuación de Laplace es oscilatoria a lo largo del eje Y, exponencial a lo largo del eje X

${\displaystyle \begin{array}{l}X(x)=C\exp \left(-kx\right)+D\exp \left(kx\right)\\ Y(y)=A\cos (ky)+B\sin (ky)\end{array}}$

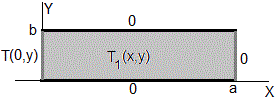
La condición de contorno T₁(x, 0)=0, hace que A=0, la condición de contorno T₁(x, b)=0, hace que sin(kb)=0, kb=nπ (n=1,2,3...). En consecuencia

${\displaystyle Y(y)=B\sin \left(\frac{n\pi }{b}y\right)}$

La temperatura T₁(x,y) en cualquier punto (x,y) del recinto rectangular 0≤x≤a, 0≤y≤b, es la superposición

${\displaystyle T_1(x,y)={\displaystyle \sum _{n=1}^{\infty }\left(C_n\exp \left(-\frac{n\pi }{b}x\right)+D_n\exp \left(\frac{n\pi }{b}x\right)\right)\sin \left(\frac{n\pi }{b}y\right)}}$

• Utilizamos la condicón de contorno T₁(0, y)

${\displaystyle T_1(\mathrm{0,}y)={\displaystyle \sum _{n=1}^{\infty }(C_n+D_n)\sin \left(\frac{n\pi }{b}y\right)}}$

Utilizamos el procedimiento para calcular los coeficientes (C_n+D_n) del desarrollo en serie de Fourier de una función periódica

${\displaystyle \begin{array}{l}T(\mathrm{0,}y)\sin \left(\frac{m\pi }{b}y\right)dy={\displaystyle \underset{0}{\overset{b}{\int }}\left\{{\displaystyle \sum _{n=1}^{\infty }(C_n+D_n)\sin \left(\frac{n\pi }{b}y\right)\sin \left(\frac{m\pi }{b}y\right)}\right\}dy}\\ {\displaystyle \underset{0}{\overset{b}{\int }}T(\mathrm{0,}y)\sin \left(\frac{m\pi }{b}y\right)dy={\displaystyle \sum _{n=1}^{\infty }(C_n+D_n){\displaystyle \underset{0}{\overset{b}{\int }}\sin \left(\frac{n\pi }{b}y\right)\sin \left(\frac{m\pi }{b}y\right)dy}}}\\ {\displaystyle \underset{0}{\overset{b}{\int }}T(\mathrm{0,}y)\sin \left(\frac{n\pi }{b}y\right)dy=\frac{b}{2}(C_n+D_n)}\end{array}}$

Por ejemplo, si T₁(0, y)=y

${\displaystyle \begin{array}{l}-\frac{b^2}{n\pi }\cos (n\pi )=\frac{b}{2}(C_n+D_n)\\ C_n+D_n=-\frac{2b}{n\pi }{\left(-1\right)}^n\end{array}}$

• La otra condición de contorno es T₁(a, y)=0

${\displaystyle \begin{array}{l}{T}_1(a,y)={\displaystyle \sum _{n=1}^{\infty }\left(C_n\exp \left(-\frac{n\pi }{b}a\right)+D_n\exp \left(\frac{n\pi }{b}a\right)\right)\sin \left(\frac{n\pi }{b}y\right)=0}\\ C_n\exp \left(-\frac{n\pi }{b}a\right)+D_n\exp \left(\frac{n\pi }{b}a\right)=0\end{array}}$

En el sistema de dos ecuaciones despejamos C_n y D_n

${\displaystyle C_n=\frac{-\frac{b}{n\pi }{\left(-1\right)}^n\exp \left(\frac{n\pi }{b}a\right)}{\sinh \left(\frac{n\pi }{b}a\right)},D_n=\frac{\frac{b}{n\pi }{\left(-1\right)}^n\exp \left(-\frac{n\pi }{b}a\right)}{\sinh \left(\frac{n\pi }{b}a\right)}}$

El primer sumando T₁(x,y) es

${\displaystyle T_1(x,y)=\frac{2b}{\pi }{\displaystyle \sum _{n=1}^{\infty }\frac{{\left(-1\right)}^{n+1}}{n}\frac{\sinh \left(\frac{n\pi }{b}(a-x)\right)}{\sinh \left(\frac{n\pi a}{b}\right)}\sin \left(\frac{n\pi }{b}y\right)}}$

Segundo sumando

La solución de la ecuación de Laplace es oscilatoria a lo largo del eje X, exponencial a lo largo del eje Y

${\displaystyle \begin{array}{l}X(x)=A\sin (kx)+B\cos (kx)\hfill \\ Y(y)=C\exp (ky)+D\exp (-ky)\hfill \end{array}}$

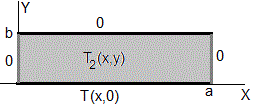
La condición de contorno T₂(0, y)=0, hace que B=0, la condición de contorno T₂(a, y)=0, hace que sin(ka)=0, ka=nπ (n=1,2,3...). En consecuencia

${\displaystyle X(x)=A\sin \left(\frac{n\pi }{a}x\right)}$

La temperatura T₂(x,y) en cualquier punto (x,y) del recinto rectangular 0≤x≤a, 0≤y≤b, es la superposición

${\displaystyle T_2(x,y)={\displaystyle \sum _{n=1}^{\infty }\left(C_n\exp \left(-\frac{n\pi }{a}y\right)+D_n\exp \left(\frac{n\pi }{a}y\right)\right)\sin \left(\frac{n\pi }{a}x\right)}}$

• Utilizamos la condicón de contorno T₂(x,0)

${\displaystyle T_2(x\mathrm{,0})={\displaystyle \sum _{n=1}^{\infty }(C_n+D_n)\sin \left(\frac{n\pi }{a}x\right)}}$

Utilizamos el procedimiento para calcular los coeficientes (C_n+D_n) del desarrollo en serie de Fourier de una función periódica

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{a}{\int }}{T}_2(x\mathrm{,0})\sin \left(\frac{m\pi }{a}x\right)dx}={\displaystyle \underset{0}{\overset{a}{\int }}\left\{{\displaystyle \sum _{n=1}^{\infty }(C_n+D_n)\sin \left(\frac{n\pi }{a}x\right)\sin \left(\frac{m\pi }{a}x\right)}\right\}dx}\\ {\displaystyle \underset{0}{\overset{a}{\int }}{T}_2(x\mathrm{,0})\sin \left(\frac{m\pi }{a}x\right)dx}={\displaystyle \sum _{n=1}^{\infty }(C_n+D_n){\displaystyle \underset{0}{\overset{a}{\int }}\sin \left(\frac{n\pi }{a}x\right)\sin \left(\frac{m\pi }{a}x\right)dx}}\\ {\displaystyle \underset{0}{\overset{a}{\int }}{T}_2(x\mathrm{,0})\sin \left(\frac{m\pi }{a}x\right)dx}=\frac{a}{2}(C_n+D_n)\end{array}}$

Por ejemplo, si T₂(x, 0)=x

${\displaystyle \begin{array}{l}-\frac{a^2}{n\pi }\cos (n\pi )=\frac{a}{2}(C_n+D_n)\\ C_n+D_n=-\frac{2a}{n\pi }{\left(-1\right)}^n\end{array}}$

• La otra condición de contorno es T₂(x, b)=0

$\begin{array}{l}{T}_2(x,b)={\displaystyle \sum _{n=1}^{\infty }\left(C_n\exp \left(-\frac{n\pi }{a}b\right)+D_n\exp \left(\frac{n\pi }{a}b\right)\right)}\sin \left(\frac{n\pi }{a}x\right)=0\\ C_n\exp \left(-\frac{n\pi }{a}b\right)+D_n\exp \left(\frac{n\pi }{a}b\right)=0\end{array}$

En el sistema de dos ecuaciones despejamos C_n y D_n

El segundo sumando T₂(x,y) es

${\displaystyle T_2(x,y)=\frac{2a}{\pi }{\displaystyle \sum _{n=1}^{\infty }\frac{{\left(-1\right)}^{n+1}}{n}\frac{\sinh \left(\frac{n\pi }{a}(b-y)\right)}{\sinh \left(\frac{n\pi b}{a}\right)}\sin \left(\frac{n\pi }{a}x\right)}}$

La temperatura en un punto (x,y) del rectángulo de dimensiones a y b es la suma de las dos contribuciones, T(x,y)=T₁(x,y)+T₂(x,y)

${\displaystyle T(x,y)=\frac{2b}{\pi }{\displaystyle \sum _{n=1}^{\infty }\frac{{\left(-1\right)}^{n+1}}{n}\frac{\sinh \left(\frac{n\pi }{b}(a-x)\right)}{\sinh \left(\frac{n\pi a}{b}\right)}\sin \left(\frac{n\pi }{b}y\right)}+\frac{2a}{\pi }{\displaystyle \sum _{n=1}^{\infty }\frac{{\left(-1\right)}^{n+1}}{n}\frac{\sinh \left(\frac{n\pi }{a}(b-y)\right)}{\sinh \left(\frac{n\pi b}{a}\right)}\sin \left(\frac{n\pi }{a}x\right)}}$

Definimos la función que calcula la temperatura T(x,y) tomando los N primeros términos del desarrollo en serie

function z = laplace_temperatura_1(x,y, N, a,b)
    z1=0;
    for n=1:N
        z1=z1+(-1)^(n+1)*sin(n*pi*x/a).*sinh(n*pi*(b-y)/a)/(n*sinh(n*pi*b/a));
    end
    z1=z1*2*a/pi;
    z2=0;
    for n=1:N
        z2=z2+(-1)^(n+1)*sin(n*pi*y/b).*sinh(n*pi*(a-x)/b)/(n*sinh(n*pi*a/b));
    end
    z2=z2*2*b/pi;
    z=z1+z2;
end

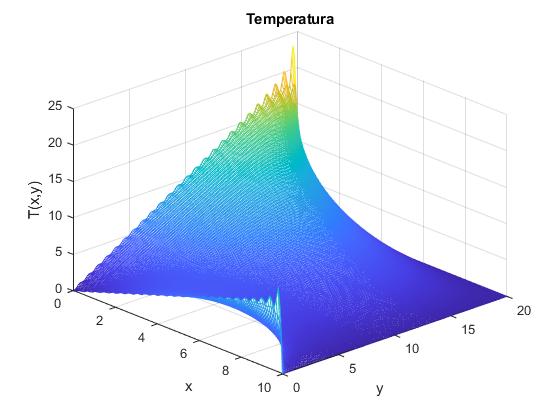
Creamos un script para representar la temperatura T(x,y) en el recinto rectangular 0≤x≤a e 0≤y≤b, con a=10 y b=20. Se han tomado N=50 términos del desarrollo en serie

a=10; %dimensiones del recinto
b=20;
N=50; %número de términos
[x,y] = meshgrid(0:0.1:a, 0:0.1:b);
z=laplace_temperatura_1(x,y, N, a,b);
mesh(x,y,z)
xlabel('x')
ylabel('y')
zlabel('T(x,y)')
title('Temperatura')
view(47,32)

Referencias

Physics 116C Home Page---Fall 2011, VI. Solutions to Homework Problem Sets and Exams. Problems 9, 11