Conducción del calor en una varilla

Hemos estudiado la conducción del calor a lo largo de una varilla de longitud L cuyos extremos están a temperaturas fijas.

Definimos la función u(x,t)=T(x,t)-T(x,∞), en términos de esta nueva función, la ecuación de la conducción del calor, las condición inicial en el instante t=0, y las condiciones de contorno en x=0 y en x=L se escriben

${\displaystyle \begin{array}{l}\frac{1}{\alpha }\frac{\partial u}{\partial t}=\frac{{\partial }^{2}u}{\partial x^2}0<x<Lt>0\\ \text{contorno}\Rightarrow u(\mathrm{0,}t)=0u(L,t)=0\\ \text{inicial}\Rightarrow u(x\mathrm{,0})\end{array}}$

La solución de la ecuación de la conducción del calor era

${\displaystyle u(x,t)={\displaystyle \sum _{n=1}^{\infty }{A}_n\exp \left(-\alpha \frac{n^2{\pi }^2}{L^2}t\right)\sin \left(n\pi \frac{x}{L}\right)}}$

Los coeficientes A_n venían determinados por la distribución inicial de temperaturas u(x,0) de la varilla

Una varilla con fuente de calor incorporada

Vamos a incorporar a la varilla una fuente de calor, hemos de resolver la ecuación del calor modificada con las mismas condiciones de contorno

${\displaystyle \begin{array}{l}\frac{1}{\alpha }\frac{\partial u}{\partial t}=\frac{{\partial }^{2}u}{\partial x^2}+q(x)0<x<Lt>0\\ \text{contorno}\Rightarrow u(\mathrm{0,}t)=0u(L,t)=0\\ \text{inicial}\Rightarrow u(x\mathrm{,0})\end{array}}$

Cuando le añadimos el término q(x) a la ecuación del calor, la solución no se puede separar en producto de dos términos uno que dependa de x, F(x) y otro que dependa de t, G(t), de modo que la solución se pueda expresar como producto de dichas funciones (variables separadas) u(x,t)=F(x)·G(t)

Buscamos una solución, similar pero con el término T_n(t) desconocido

${\displaystyle u(x,t)={\displaystyle \sum _{n=1}^{\infty }{T}_n(t)\sin \left(n\pi \frac{x}{L}\right)}}$

En el instante t=0, T_n(0), son los coeficientes del desarrollo en serie de la distribución inicial de temperaturas

${\displaystyle u(x\mathrm{,0})={\displaystyle \sum _{n=1}^{\infty }{T}_n(0)\sin \left(n\pi \frac{x}{L}\right)}}$

Desarrollamos en serie el término q(x) que describe la fuente de calor

${\displaystyle q(x)={\displaystyle \sum _{n=1}^{\infty }{q}_n\sin \left(n\pi \frac{x}{L}\right)}}$

En ambos casos, para obtener los coeficientes, T_n(0) y q_n se siguen los siguientes pasos

Multiplicamos ambos miembros por sin(mπx/L) e integramos entre 0 y L, para ello, hacemos el cambio de variable z=πx/L, dz=πdx/L

${\displaystyle {\displaystyle \underset{0}{\overset{L}{\int }}q(x)\sin \left(m\pi \frac{x}{L}\right)dx}={\displaystyle \sum _{n=1}^{\infty }{q}_n{\displaystyle \underset{0}{\overset{L}{\int }}\sin \left(n\pi \frac{x}{L}\right)}}\sin \left(m\pi \frac{x}{L}\right)dx}$

El resultado de la integral del segundo miembro cuando m≠n y cuando m=n es

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{L}{\int }}\sin \left(m\pi \frac{x}{L}\right)\sin \left(n\pi \frac{x}{L}\right)dx}=\frac{L}{\pi }{\displaystyle \underset{0}{\overset{\pi }{\int }}\sin \left(mz\right)\sin \left(nz\right)dz}\\ \left(1-\frac{n^2}{m^2}\right){\displaystyle \underset{0}{\overset{\pi }{\int }}\sin \left(mz\right)\sin \left(nz\right)dz}={-\frac{1}{m}\sin \left(nz\right)\cos \left(mz\right)+\frac{n}{m^2}\cos \left(nz\right)\sin \left(nz\right)|}_0^{\pi }=0\\ {\displaystyle \underset{0}{\overset{\pi }{\int }}{\sin }^2\left(nz\right)dz}=\frac{1}{2}{\displaystyle \underset{0}{\overset{\pi }{\int }}\left(1-\cos \left(2nz\right)\right)dz}=\frac{1}{2}{\left(z-\frac{1}{2n}\sin \left(2nz\right)\right)|}_0^{\pi }=\frac{\pi }{2}\end{array}}$

Despejamos q_n

${\displaystyle q_n=\frac{2}{L}{\displaystyle \underset{0}{\overset{L}{\int }}q(x)\sin \left(n\pi \frac{x}{L}\right)}dx}$

Despejamos T_n(0)

${\displaystyle T_n(0)=\frac{2}{L}{\displaystyle \underset{0}{\overset{L}{\int }}u(x\mathrm{,0})\sin \left(n\pi \frac{x}{L}\right)}dx}$

Introducimos la expresión de u(x,t) en la ecuación del calor

${\displaystyle \frac{1}{\alpha }{\displaystyle \sum _{n=1}^{\infty }\frac{d{T}_n(t)}{dt}\sin \left(n\pi \frac{x}{L}\right)}={\displaystyle \sum _{n=1}^{\infty }\left(-\frac{n^2{\pi }^2}{L^2}\right)}{T}_n(t)\sin \left(n\pi \frac{x}{L}\right)+{\displaystyle \sum _{n=1}^{\infty }{q}_n\sin \left(n\pi \frac{x}{L}\right)}}$

El resultado es una ecuación en T_n(t) que integramos

${\displaystyle \begin{array}{l}\frac{1}{\alpha }\frac{d{T}_n(t)}{dt}=-\frac{n^2{\pi }^2}{L^2}{T}_n(t)+q_n\\ T_n(t)=\frac{4}{n^2{\pi }^2}{q}_n+c_n\exp \left(-\alpha \frac{n^2{\pi }^2}{4}t\right)\end{array}}$

donde c_n es una constante a determinar a partir de la distribución inicial de temperaturas u(x,0) en el instante t=0.

${\displaystyle T_n(0)=\frac{4}{n^2{\pi }^2}{q}_n+c_n}$

Solución completa

La solución de la ecuación del calor u(x,t), que incorpora el término que describe el calor q(x) que se genera en el interior de la varilla es

${\displaystyle u(x,t)={\displaystyle \sum _{n=1}^{\infty }\left(\frac{4}{n^2{\pi }^2}{q}_n+\left(T_n(0)-\frac{4}{n^2{\pi }^2}{q}_n\right)\exp \left(-\alpha \frac{n^2{\pi }^2}{4}t\right)\right)}\sin \left(n\pi \frac{x}{L}\right)}$

Ejemplo

Sea una varilla de longitud L=2. La distribución inicial de temperaturas es u(x,0)=2x-x². Las temperaturas en los extremos de la varilla u(0,t)=0, y u(L,t)=0. La fuente de calor está descrita por la función

${\displaystyle q(x)=\{\begin{array}{l}x0<x<1\\ 2-x1<x<2\end{array}}$

Los coeficientes q_n del desarrollo en serie de q(x) son

${\displaystyle \begin{array}{l}{q}_n={\displaystyle \underset{0}{\overset{2}{\int }}q(x)\sin \left(n\pi \frac{x}{L}\right)}dx={\displaystyle \underset{0}{\overset{1}{\int }}x\sin \left(n\pi \frac{x}{2}\right)dx+}{\displaystyle \underset{1}{\overset{2}{\int }}(2-x)\sin \left(n\pi \frac{x}{2}\right)dx=}\\ \frac{8}{n^2{\pi }^2}\sin \left(\frac{n\pi }{2}\right)\end{array}}$

Los coeficientes T_n(0) del desarrollo en serie de u(x,0) son

${\displaystyle T_n(0)=\frac{2}{L}{\displaystyle \underset{0}{\overset{L}{\int }}u(x\mathrm{,0})\sin \left(n\pi \frac{x}{L}\right)}dx={\displaystyle \underset{0}{\overset{2}{\int }}(2x-x^2)\sin \left(n\pi \frac{x}{2}\right)}dx=\frac{16}{n^3{\pi }^3}\left(1-\cos (n\pi )\right)}$

La solución completa u(x,t) es

${\displaystyle u(x,t)=\frac{32}{{\pi }^3}{\displaystyle \sum _{n=\mathrm{1,3,5,...}}^{\infty }\frac{1}{n^3}\left(\frac{{\left(-1\right)}^{\frac{n-1}{2}}}{n\pi }+\left(1-\frac{{\left(-1\right)}^{\frac{n-1}{2}}}{n\pi }\right)\exp \left(-\alpha \frac{n^2{\pi }^2}{4}t\right)\right)}\sin \left(n\pi \frac{x}{2}\right)}$

x=linspace(0,2,100);
hold on
for t=0:3
    T=zeros(1,length(x));
    for n=1:2:99
       T=T+((-1)^((n-1)/2)/(n*pi)+(1-(-1)^((n-1)/2)/(n*pi))*
exp(-n^2*pi^2*t/4))*sin(n*pi*x/2)*32/(n^3*pi^3);
    end
    plot(x,T,'displayName',num2str(t));
end
hold off
title('Evolución de la temperatura de una varilla')
xlabel('Longitud')
ylabel('Temperatura')
legend('-DynamicLegend','location','northeast')
grid on
hold off 

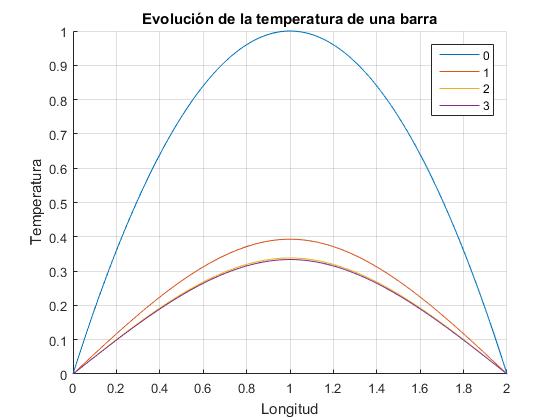
Estado estacionario

Observamos en la representación gráfica que a partir de t=3 se alcanza una distribución de temperaturas que parece que no cambia apreciablemente con el tiempo. Se ha alcanzado el estado estacionario

En el estado estacionario, la solución u(x,t) no depende de t, solamente de x, de modo que la ecuación del calor se escribe

${\displaystyle \frac{d^{2}u}{d{x}^2}+q(x)=00<x<Lt>0}$

Integramos dos veces para obtener u(x)

${\displaystyle \begin{array}{l}\frac{du}{dx}=-{\displaystyle \int q(x)dx}+c_1=f(x)+c_1\\ u(x,\infty )={\displaystyle \int f(x)dx}+c_{1}x+c_2\end{array}}$

Las constntes c₁ y c₂ se determinan sabiendo que las temperaturas en los extremos de la varilla son u(0,t) y u(L,t)

Determinamos el estado estacionario con los datos del ejemplo anterior. Dado q(x)

${\displaystyle q(x)=\{\begin{array}{l}x0<x<1\\ 2-x1<x<2\end{array}}$

Integramos dos veces

${\displaystyle u(x,\infty )=\{\begin{array}{l}-\frac{x^3}{6}+c_{1}x+c_{2}0<x<1\\ -x^2+\frac{x^3}{6}+k_{1}x+k_{2}1<x<2\end{array}}$

Las temperaturas en los extremos de la varilla son u(0,t)=0 y u(L,t)=0

${\displaystyle \{\begin{array}{l}{c}_2=0\\ -\frac{8}{3}+2k_1+k_2=0\end{array}}$

La función u(x,∞), es continua en x=1, y también su derivada primera

${\displaystyle \{\begin{array}{l}{c}_1=-\frac{2}{3}+k_1+k_2\\ c_1=-1+k_1\end{array}}$

El estado estacionario u(x,∞) es

${\displaystyle u(x,\infty )=\{\begin{array}{l}-\frac{x^3}{6}+\frac{1}{2}x0<x<1\\ -x^2+\frac{x^3}{6}+\frac{3}{2}x-\frac{1}{3}1<x<2\end{array}}$

Añadimos al script la función que describe el estado estacionario y la representamos mediante el comando fplot, confirmando que para t=3 se está próximo al estado estacionario

x=linspace(0,2,100);
%estado estacionario
f=@(x) (x<1)*(-x^3/6+x/2)+(x>=1)*(-x^2+x^3/6+3*x/2-1/3);
hold on
%estado transitorio
for t=0:3
    T=zeros(1,length(x));
    for n=1:2:99
       T=T+((-1)^((n-1)/2)/(n*pi)+(1-(-1)^((n-1)/2)/(n*pi))
*exp(-n^2*pi^2*t/4))*sin(n*pi*x/2)*32/(n^3*pi^3);
    end
    plot(x,T,'displayName',num2str(t));
end
fplot(f,[0,2], 'color','k')
hold off
title('Evolución de la temperatura de una varilla')
xlabel('Longitud')
ylabel('Temperatura')
legend('-DynamicLegend','location','northeast')
grid on
hold off 

Referencias

El ejemplo que aparece en esta página ha sido tomado del documento titulado: Chapter 5. Separation of variables. http://faculty.uca.edu/darrigo/Students/M4315/Fall%202005/sep-var.pdf