Consideremos una esfera de radio R en la cual la distribución inicial de temperaturas y las condiciones de contorno tienen simetría esférica. Las superficies isotérmicas son superficies esféricas concéntricas y la temperatura es una función únicamente de la distancia radial r y del tiempo t.

La ecuación de la conducción del calor apropiada para resolver este problema es

${\displaystyle \begin{array}{l}\frac{1}{\alpha }\frac{\partial T}{\partial t}=\frac{1}{r^2}\frac{\partial }{\partial r}\left(r^2\frac{\partial T}{\partial r}\right)\\ \frac{1}{\alpha }\frac{\partial T}{\partial t}=\frac{2}{r}\frac{\partial T}{\partial r}+\frac{{\partial }^{2}T}{\partial r^2}\end{array}}$

La esfera se calienta hasta una temperatura uniforme T₀ (distribución inicial de temperaturas T(r, 0)=T₀. En el instante t=0, se pone a enfriar en un ambiente cuya temperatura es constante T_s, perdiendo calor por radiación. La condición de contorno es

${\displaystyle {\frac{\partial T(r,t)}{\partial r}|}_{r=R}+h\left(T(R,t)-T_s\right)=0}$

En el estado estacionario, después de un tiempo t→∞, la temperatura final de la esfera será T(r,∞)=T_s, la temperatura del ambiente.

Solución de la ecuación de la conducción del calor

Definimos la función u(r,t)=T(r,t)-T(r,∞), en términos de esta nueva función, la ecuación de la conducción del calor, las condición inicial en el instante t=0, y las condiciones de contorno en r=R se escriben

${\displaystyle \begin{array}{l}\frac{1}{\alpha }\frac{\partial u}{\partial t}=\frac{{\partial }^{2}u}{\partial r^2}+\frac{2}{r}\frac{\partial u}{\partial r}0<r<Lt>0\\ ·\text{contorno}\Rightarrow {\frac{\partial u(r,t)}{\partial r}|}_{r=R}+hu(R,t)=0\\ ·\text{inicial}\Rightarrow u(x\mathrm{,0})=T_0-T_s\end{array}}$

Si hacemos la sustitución v(r,t)=r·u(r,t) nos queda la educación diferencial en derivadas parciales

${\displaystyle \frac{\partial v}{\partial t}=\alpha \frac{{\partial }^{2}v}{{\partial }^{2}r}}$

La condición de contorno se escribe ahora

${\displaystyle {\frac{\partial v(r,t)}{\partial r}|}_{r=R}+\left(h-\frac{1}{R}\right)v(R,t)=0}$

Buscamos soluciones de la forma v(r,t)=F(r)·G(t) (variables separadas)

${\displaystyle \begin{array}{l}\frac{\partial v(r,t)}{\partial t}=\alpha \frac{{\partial }^{2}v(r,t)}{{\partial }^{2}r}\\ \frac{1}{\alpha }\frac{1}{G(t)}\frac{dG(t)}{dt}=\frac{1}{F(r)}\frac{d^{2}F(r)}{d^{2}r}=-{\omega }^2\end{array}}$

Integramos la primara ecuación diferencial

${\displaystyle \begin{array}{l}\frac{dG(t)}{dt}+\alpha {\omega }^{2}G(t)=0\\ G(t)=G(0)·\exp (-\alpha {\omega }^{2}t)\end{array}}$

Integramos la segunda ecuación diferencial

${\displaystyle \frac{d^{2}F(r)}{d^{2}r}+{\omega }^{2}F(r)=0}$

Es una ecuación diferencial similar a la de un Movimiento Armónico Simple. La solución es F(r)=A·sin(ωr)+B·cos(ωr)

En primer lugar, F(0)=0 ya que u(r,t) tiene que ser finito cuando r=0, recuérdese que u(r,t)=v(r,t)/r y v(r, t)=F(r)·G(t). Esto implica que B=0

Condiciones de contorno

Dado que v(r,t)=A·sin(ωr), la condición de contorno da lugar a una ecuación transcendente en k=ωR

${\displaystyle \begin{array}{l}\omega \cos \left(\omega R\right)+\left(h-\frac{1}{R}\right)\sin \left(\omega R\right)=0\\ k\cos \left(k\right)+\left(hR-1\right)\sin \left(k\right)=0\end{array}}$

La solución v(r,t) es la superposición de los productos F_n(r)·G_n(t). La solución de la ecuación de la conducción del calor r·u(r,t)=v(r,t)

${\displaystyle \begin{array}{l}r·u(r,t)={\displaystyle \sum _{n=1}^{\infty }{A}_n\sin \left({\omega }_{n}r\right)}\exp \left(-\alpha {\omega }_n^{2}t\right)\\ r·u(r,t)={\displaystyle \sum _{n=1}^{\infty }{A}_n\sin \left(k_n\frac{r}{R}\right)}\exp \left(-\alpha \frac{k_n^2}{R^2}t\right)\end{array}}$

Condición inicial

Los coeficientes A_n se determinan a partir de la distribución inicial de temperaturas u(r,0)=T₀-T_s

${\displaystyle r·u(r\mathrm{,0})={\displaystyle \sum _{n=1}^{\infty }{A}_n\sin \left(k_n\frac{r}{R}\right)}}$

Despejamos A_n utilizando las relaciones de ortogonalidad, véase más abajo

${\displaystyle \left(T_0-T_s\right){\displaystyle \underset{0}{\overset{R}{\int }}r}\sin \left(k_m\frac{r}{R}\right)dr=A_m{\displaystyle \underset{0}{\overset{R}{\int }}{\sin }^2\left(k_m\frac{r}{R}\right)dr}}$

Haciendo el cambio de variable x=r/R

${\displaystyle \begin{array}{l}{R}^2\left(T_0-T_s\right){\displaystyle \underset{0}{\overset{1}{\int }}x}\sin \left(k_{m}x\right)dx=A_{m}R{\displaystyle \underset{0}{\overset{1}{\int }}{\sin }^2\left(k_{m}x\right)dx}\\ A_m=\frac{2R\left(T_0-T_s\right)\left(-\cos \left(k_m\right)+\frac{1}{k_m}\sin \left(k_m\right)\right)}{k_m-\sin \left(k_m\right)\cos \left(k_m\right)}\end{array}}$

Cambiando m por n y teniendo en cuenta que k_n son las raíces de la ecuación transcendente kcos(k)+(hR-1)sin(k)=0. Los coeficientes A_n valen

${\displaystyle A_n=\frac{2h{R}^2\left(T_0-T_s\right)\sin \left(k_n\right)}{k_n^2-(1-hR){\sin }^2\left(k_n\right)}}$

Solución completa

La temperatura T(r,t) en cualquier punto a una distancia r del centro de la esfera, en un instante t, se compone de la suma de la temperatura en el estado estacionario T_s y de una serie rápidamente convergente que describe el estado transitorio.

${\displaystyle \begin{array}{l}r·u(r,t)=2h{R}^2\left(T_0-T_s\right){\displaystyle \sum _{n=1}^{\infty }\frac{\sin \left(k_n\right)}{k_n^2-(1-hR){\sin }^2\left(k_n\right)}\sin \left(k_n\frac{r}{R}\right)}\exp \left(-\alpha \frac{k_n^2}{R^2}t\right)\\ T(r,t)=u(r,t)+T(r,\infty )=\\ T_s+\frac{2h{R}^2\left(T_0-T_s\right)}{r}{\displaystyle \sum _{n=1}^{\infty }\frac{\sin \left(k_n\right)}{k_n^2-(1-hR){\sin }^2\left(k_n\right)}\sin \left(k_n\frac{r}{R}\right)}\exp \left(-\alpha \frac{k_n^2}{R^2}t\right)\end{array}}$

Ejemplo

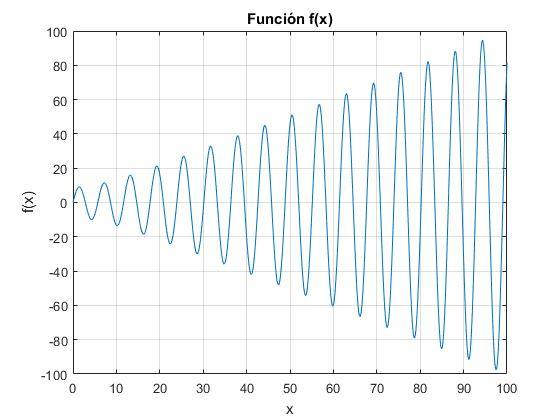
Representamos gráficamente la función f(x)=x·cos(x)+(hR-1)sin(x), para estimar aproximadamente donde se encuentran las raíces de la ecuación transcendente f(x)=0.

>> hR=10;
>> f=@(x) x*cos(x)+(hR-1)*sin(x);
>> fplot(f,[0,100])
>> xlabel('x')
>> ylabel('f(x)')
>> title('Función f(x)')
>> grid on

Definimos la función temperatura_8 para calcular la distribución de temperaturas a lo largo de de la dirección radial de la esfera en el instante t

function [r,T]=temperatura_8(T0,Ts,R,k,a2,t)
   r=linspace(eps,R,100);
    if(t==0)
       T=T0*ones(1,length(r));
       return;
   end  
   T=Ts*ones(1,length(r));
   for n=1:length(k)
        an=2*R*(T0-Ts)*(-cos(k(n))+sin(k(n))/k(n))/(k(n)-cos(k(n))*sin(k(n)));
        T=T+(an./r)*exp(-k(n)^2*t/(a2*R^2)).*sin(k(n)*r/R);
   end
end

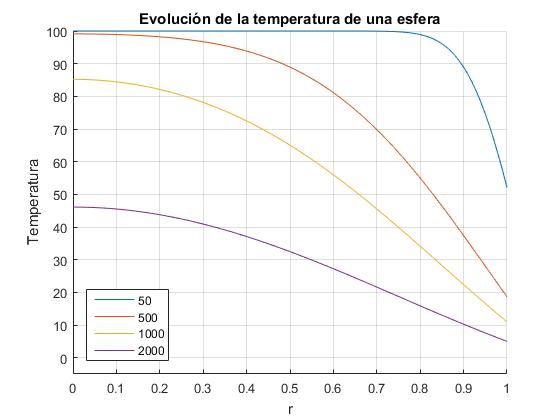
Creamos un script en el que establecemos la temperatura inicial T₀, la temperatura ambiente T_s, el radio R de la esfera, el material del cual está hecho la esfera, (parámetro α) y el parámetro hR, cuanto mayor sea su valor, mayor son las pérdidas por radiación de la superficie del cilindro. El script calcula un número elevado de raíces k_n de la ecuación transcendente y representa la distribución radial de temperaturas de la esfera en varios instantes.

T0=100; %temperatura inicial
Ts=0; %temperatura ambiente
alfa=11352; %Coeficiente, 1/alfa del aluminio
R=1; % radio de la esfera
hR=10; %pérdida de calor por radiación

%raíces
x=linspace(0,100,100);
f=@(x) x.*cos(x)+(hR-1)*sin(x);
k=raices(f,x);

hold on
axis([0 1 -5 100]);
for t=[50 500 1000 2000]
    [x,T]=temperatura_8(T0,Ts,R,k,alfa,t);
    plot(x,T,'displayName',num2str(t));
end
title('Evolución de la temperatura de una esfera')
xlabel('r')
ylabel('Temperatura')
legend('-DynamicLegend','location','southwest')
grid on
hold off  

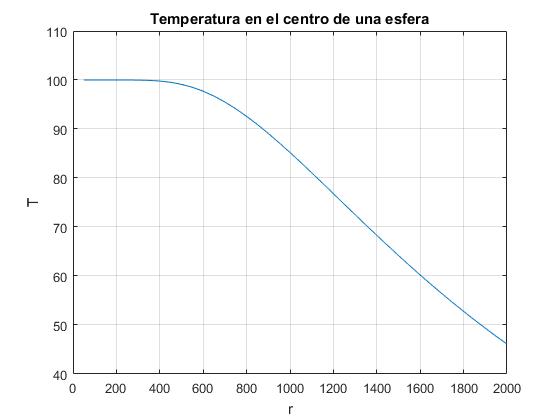
Temperatura en el centro de la esfera

Temperatura en el centro de la esfera cuando r→0

${\displaystyle \underset{r\to 0}{\lim }\frac{\sin \left(k_n\frac{r}{R}\right)}{k_{n}r}=\frac{1}{R}}$

en función del tiempo t

${\displaystyle T(\mathrm{0,}t)=T_s+2hR\left(T_0-T_s\right){\displaystyle \sum _{n=1}^{\infty }\frac{k_n\sin \left(k_n\right)}{k_n^2-(1-hR){\sin }^2\left(k_n\right)}}\exp \left(-\alpha \frac{k_n^2}{R^2}t\right)}$

function T=temperatura_9(T0,Ts,R,k,a2,t)
    if(t==0)
       T=T0;
       return;
   end  
   T=Ts;
   for n=1:length(k)
        an=2*(T0-Ts)*k(n)*(-cos(k(n))+sin(k(n))/k(n))
/(k(n)-cos(k(n))*sin(k(n)));
        T=T+an*exp(-k(n)^2*t/(a2*R^2));
   end
end

T0=100; %temperatura inicial
Ts=0; %temperatura ambiente
alfa=11352; %Coeficiente, 1/alfa del aluminio
R=1; % radio de la esfera
hR=10;

%raíces
x=linspace(0,100,100);
f=@(x) x.*cos(x)+(hR-1)*sin(x);
k=raices(f,x);

axis([0 1 -5 100]);
T=T0*ones(1,length(t));
t=50:50:2000;
for i=1:length(t)
    T(i)=temperatura_9(T0,Ts,R,k,alfa,t(i));
end
plot(t,T);
title('Temperatura en el centro de una esfera')
xlabel('r')
ylabel('T')
grid on

Una vez obtenidas las raíces k_n de la ecuación transcendente, comprobamos las relaciones de ortogonalidad entre las funciones sin(k_nx/R) y sin(k_mx/R) con m≠n

${\displaystyle {\displaystyle \underset{0}{\overset{R}{\int }}\sin \left(k_n\frac{r}{R}\right)\sin \left(k_m\frac{r}{R}\right)dr}=0m\ne n}$

>> f=@(x) sin(k(1)*x/R).*sin(k(2)*x/R);
>> integral(f,0,R)
ans =  -4.0766e-17
>> f=@(x) sin(k(5)*x/R).*sin(k(9)*x/R);
>> integral(f,0,R)
ans =  -5.5511e-17