Una placa uniformemente iluminada

En la página titulada Se calienta una placa expuesta al Sol Consideramos una placa de área A y espesor e, que está a la temperatura ambiente T_s. La superficie de la placa está pintada de negro. En un instante dado, se expone al Sol que ilumina la placa con una intensidad constante de I W/m². Determinamos la evolución de la temperatura T de la placa a medida que transcurre el tiempo.

Supongamos una placa de espesor L, a la temperatura ambiente T_s, que se expone al sol que ilumina uniformemente su cara x=0, con q W/m²

Para calcular la temperatura T(x,t) en un punto x de la placa y en un instante t, resolvemos la ecuación de la conducción del calor

$\frac{1}{α} \frac{\partial T}{\partial t} = \frac{\partial^{2} T}{\partial x^{2}} 0 < x < L t > 0$

Las condiciones de contorno en el extremo izquierdo x=0, y en el extremo derecho x=L son:

$\begin{array}{l} {\frac{\partial T (x, t)}{\partial x} |}_{x = 0} = h_{1} (T (0, t) - T_{s}) - \frac{q}{K} t > 0 \\ {- \frac{\partial T (x, t)}{\partial x} |}_{x = L} = h_{2} (T (L, t) - T_{s}) t > 0 \end{array}$

El primer término, proporcional a la diferencia de temperaturas T(0,t)-T_s entre el extremo izquierdo x=0 de la placa y la temperatura ambiente, da cuenta de las pérdidas de calor que experimenta la placa a través de su cara anterior. El segundo término, q es el fujo de calor uniforme (energía por unidad de área y de tiempo) que incide sobre dicha superficie. El término proporcional a la diferencia de temperaturas T(L,t)-T_s entre el extremo derecho x=L de la placa y la temperatura ambiente, da cuenta de las pérdidas de calor que experimenta la placa a través de su cara posterior. Las constantes de proporcionalidad h₁ y h₂ podrían ser diferentes

La condición inicial, es la de una placa a la temperatura uniforme T(x,0)=T_s del ambiente

El estado estacionario

Al cabo de cierto tiempo, teóricamente infinito, se establece un estado estacionario en el que la temperatura de cada punto de la placa no varía con el tiempo.

$\begin{array}{l} \frac{\partial^{2} T}{\partial x^{2}} = 0 \\ T (x) = A x + B \end{array}$

donde A y B se determinan a partir de las condiciones de contorno en x=0

$A = h_{1} (B - T_{s}) - \frac{q}{K}$

y en x=L

$- A = h_{2} (A L + B - T_{s})$

Despejamos A y B del sistema de dos ecuaciones

$T (x, \infty) = (\frac{q}{K}) (\frac{- h_{2} x + h_{2} L + 1}{h_{1} + h_{2} + h_{1} h_{2} L}) + T_{s}$

Solución de la ecuación de la conducción del calor

Definimos la función u(x,t)=T(x,t)-T(x,∞), en términos de esta nueva función, la ecuación de la conducción del calor se escibe,

$\frac{1}{α} \frac{\partial u}{\partial t} = \frac{\partial^{2} u}{\partial x^{2}} 0 < x < L t > 0$

Condición inicial

u(x,0)=T(x,0)-T(x,∞)

$u (x,0) = (\frac{q}{K}) (\frac{h_{2} x - h_{2} L - 1}{h_{1} + h_{2} + h_{1} h_{2} L})$

Condiciones de contorno

En el extremo izquierdo, x=0

$\begin{array}{l} {\frac{\partial u (x, t)}{\partial x} |}_{x = 0} = {\frac{\partial T (x, t)}{\partial x} |}_{x = 0} - {\frac{\partial T (x, \infty)}{\partial x} |}_{x = 0} \\ {\frac{\partial u (x, t)}{\partial x} |}_{x = 0} = h_{1} (T (0, t) - T_{s}) - \frac{q}{K} - (\frac{q}{K}) (\frac{- h_{2}}{h_{1} + h_{2} + h_{1} h_{2} L}) \\ {\frac{\partial u (x, t)}{\partial x} |}_{x = 0} = h_{1} (u (0, t) + T (0, \infty) - T_{s}) - (\frac{q}{K}) (\frac{h_{1} + h_{1} h_{2} L}{h_{1} + h_{2} + h_{1} h_{2} L}) \\ {\frac{\partial u (x, t)}{\partial x} |}_{x = 0} = h_{1} (u (0, t) + (\frac{q}{K}) (\frac{h_{2} L + 1}{h_{1} + h_{2} + h_{1} h_{2} L}) + T_{s} - T_{s}) - (\frac{q}{K}) (\frac{h_{1} + h_{1} h_{2} L}{h_{1} + h_{2} + h_{1} h_{2} L}) \\ {\frac{\partial u (x, t)}{\partial x} |}_{x = 0} = h_{1} u (0, t) \end{array}$

En el extremo derecho, x=L

$\begin{array}{l} {\frac{\partial u (x, t)}{\partial x} |}_{x = L} = {\frac{\partial T (x, t)}{\partial x} |}_{x = L} - {\frac{\partial T (x, \infty)}{\partial x} |}_{x = L} \\ {\frac{\partial u (x, t)}{\partial x} |}_{x = L} = - h_{2} (T (L, t) - T_{s}) - (\frac{q}{K}) (\frac{- h_{2}}{h_{1} + h_{2} + h_{1} h_{2} L}) \\ {\frac{\partial u (x, t)}{\partial x} |}_{x = L} = - h_{2} (u (L, t) + T (L, \infty) - T_{s}) + (\frac{q}{K}) (\frac{h_{2}}{h_{1} + h_{2} + h_{1} h_{2} L}) \\ {\frac{\partial u (x, t)}{\partial x} |}_{x = L} = - h_{2} (u (L, t) + (\frac{q}{K}) (\frac{1}{h_{1} + h_{2} + h_{1} h_{2} L}) + T_{s} - T_{s}) + (\frac{q}{K}) (\frac{h_{2}}{h_{1} + h_{2} + h_{1} h_{2} L}) \\ {\frac{\partial u (x, t)}{\partial x} |}_{x = L} = - h_{2} u (L, t) \end{array}$

Variables separadas

Buscamos una solución de la forma u(x, t)=F(x)·G(t), variables separadas

$\frac{1}{α} \frac{1}{G (t)} \frac{d G (t)}{d t} = \frac{1}{F (x)} \frac{d^{2} F (x)}{d x^{2}} = - ω^{2}$

Integramos la primera ecuación diferencial

$\begin{array}{l} \frac{d G (t)}{d t} + α ω^{2} G (t) = 0 \\ G (t) = G (0) \cdot \exp (- α ω^{2} t) \end{array}$

Integramos la segunda ecuación diferencial

$\frac{d^{2} F (x)}{d x^{2}} + ω^{2} F (x) = 0$

Es una ecuación diferencial similar a la de un Movimiento Armónico Simple, cuya solución es F(x)=Acos(ωx)+Bsin(ωx)

Solución general

La condición de contorno en el extremo izquierdo x=0, requiere que Bω=h₁A
La condición de contorno en el extremos derecho x=L, requiere -Aωsin(ωL)+Bωcos(ωL)=-h₂(Acos(ωL)+Bsin(ωL))

Eliminando A y B en el sistema homogéneo de dos ecuaciones y expresando la ecuación resultante en términos de k=ωL

$(h_{1} h_{2} L^{2} - k^{2}) \sin (k) + (h_{1} + h_{2}) L k \cos (k) = 0$

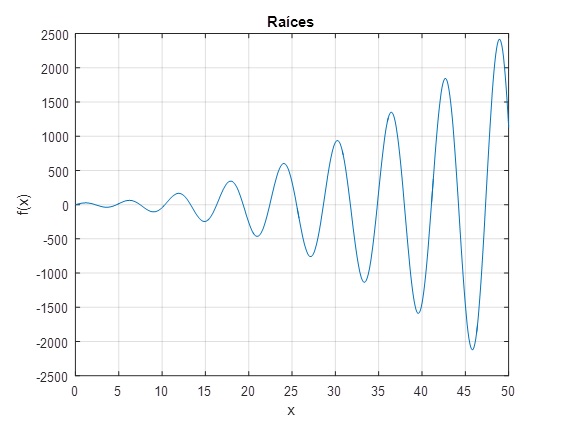
Calculamos las raíces k_n de esta ecuación transcendente

La solución completa u(x,t) es la superposición de los productos de las funciones F_n(x)·G_n(t) para cada k_n

$u (x, t) = \sum_{n = 1}^{\infty} {A_{n} \cos (k_{n} \frac{x}{L}) + B_{n} \sin (k_{n} \frac{x}{L})} \exp (- α \frac{k_{n}^{2}}{L^{2}} t)$

Coeficientes A_n y B_n

Ya que la condición de contorno en el extremo izquierdo x=0, requiere que Bω=h₁A o bien, A_n=B_nk_n/(h₁L)

$u (x, t) = \sum_{n = 1}^{\infty} B_{n} {\frac{k_{n}}{h_{1} L} \cos (k_{n} \frac{x}{L}) + \sin (k_{n} \frac{x}{L})} \exp (- α \frac{k_{n}^{2}}{L^{2}} t)$

Solamente, queda por determinar los coeficientes B_n, identificando la solución para t=0 con la condición inicial u(x,0)

$\begin{array}{l} u (x,0) = \sum_{n = 1}^{\infty} B_{n} X_{n} \\ X_{n} (x) = \frac{k_{n}}{h_{1} L} \cos (k_{n} \frac{x}{L}) + \sin (k_{n} \frac{x}{L}) \end{array}$

Multiplicando ambos miembros por X_m(x) e integrando entre 0 y L

$\int_{0}^{L} u (x,0) X_{m} (x) d x = \sum_{n = 1}^{\infty} B_{n} \int_{0}^{L} X_{m} (x) X_{n} (x) d x$

Teniendo en cuenta la relación de ortogonalidad, véase más abajo

$\int_{0}^{L} X_{m} (x) X_{n} (x) d x = 0 m \neq n$

Obtenemos los coeficientes B_m

$B_{m} = \frac{\int_{0}^{L} (\frac{q}{K}) (\frac{h_{2} x - h_{2} L - 1}{h_{1} + h_{2} + h_{1} h_{2} L}) X_{m} (x) d x}{\int_{0}^{L} X_{m}^{2} (x) d x}$

Cambiando m por n e integrando

$B_{n} = (\frac{q / K}{h_{1} + h_{2} + h_{1} h_{2} L}) \frac{(- \frac{1}{h_{1}} + \frac{h_{2} L^{2}}{k_{n}^{2}}) \sin (k_{n}) + \frac{(h_{1} + h_{2}) L}{h_{1} k_{n}} \cos (k_{n}) - \frac{L (h_{1} + h_{2} + h_{1} h_{2} L)}{h_{1} k_{n}}}{\frac{(1 + k_{n}^{2})}{2 h_{1}} + \frac{1}{4} (\frac{k_{n}}{h_{1}} - \frac{L}{k_{n}}) \sin (2 k_{n}) - \frac{1}{2 h_{1}} \cos (2 k_{n})}$

Solución completa

La solución completa es

$\begin{array}{l} u (x, t) = \sum_{n = 1}^{\infty} B_{n} (\frac{k_{n}}{h_{1} L} \cos (k_{n} \frac{x}{L}) + \sin (k_{n} \frac{x}{L})) \exp (- α \frac{k_{n}^{2}}{L^{2}} t) \\ T (x, t) = u (x, t) + T (x, \infty) = \\ T_{s} + (\frac{q}{K}) (\frac{- h_{2} x + h_{2} L + 1}{(h_{1} + h_{2} + h_{1} h_{2} L)}) {\sum_{n = 1}^{\infty} B_{n} (\frac{k_{n}}{h_{1} L} \cos (k_{n} \frac{x}{L}) + \sin (k_{n} \frac{x}{L})) \exp (- α \frac{k_{n}^{2}}{L^{2}} t)} \end{array}$

Ejemplo

Supongamos que la anchura de la placa es L=0.5 y los coeficientes h₁=10 y h₂=10. Vamos a representar gráficamente la función y=(h₁h₂L²-x²)sin(x)+(h₁+h₂)Lxcos(x), para estimar aproximadamente donde se encuentran las raíces de la ecuación transcendente.

> L=0.5; % anchura placa
>> h1=10; %pérdidas por radiación
>> h2=10; %pérdidas por radiación
>> f=@(x) (h1*h2*L^2-x^2)*sin(x)+(h1+h2)*L*x*cos(x);
>> fplot(f,[1,50])
>> grid on
>> xlabel('x')
>> ylabel('y')

La función raices calcula las raíces múltiples de la función f(x) buscando los intervalos en los que dicha función cambia de signo y utilizando la función MATLAB fzero para encontrarlas

function r = raices(f, x)
    y=f(x);
    indices=find(y(1:end-1).*y(2:end)<0);
    r=zeros(1,length(indices));
    for k=1:length(indices)
        r(k)=fzero(f, [x(indices(k)), x(indices(k)+1)]);
    end
end

Definimos la función temperatura_10 para calcular la distribución de temperaturas a lo largo de la dirección perpendicular a la placa en el instante t

function [x,T]=temperatura_10(Ts,L,h1,h2,q_K,k,a2,t)
   x=linspace(0,L,100);
   if(t==0)
       T=Ts*ones(1,length(x));
       return;
   end
      
   cte=q_K/(h1+h2+h1*h2*L);
   T=Ts+cte*(-h2*x+h2*L+1);
    
    for n=1:length(k)
       num=(-1/h1+h2*L^2/k(n)^2)*sin(k(n))+(h1+h2)*L*cos(k(n))
/(h1*k(n))-L*(h1+h2+h1*h2*L)/(h1*k(n));
       den=(1+k(n)^2)/(2*h1)+(k(n)/h1-L/k(n))*sin(2*k(n))/4-cos(2*k(n))/(2*h1);
       T=T+(cte*num/den)*exp(-k(n)^2*t/(a2*L^2))*(k(n)*cos(k(n)*x/L)
/(h1*L)+sin(k(n)*x/L));
   end
end

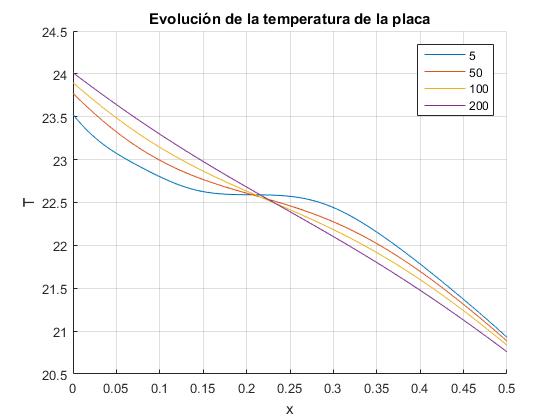
Creamos un script en el que establecemos la temperatura ambiente T_s, la anchura L de la placa, el material del cual está hecho la placa, (parámetro α), los coeficientes de pérdida de calor por radiación en ambas caras h₁ y h₂ y el cociente q/K entre el flujo de calor q que incide uniformemente sobre la cara izquierda y la conductividad térmica del material K. El script calcula un número elevado de raíces k_n de la ecuación transcendente y representa la distribución de temperaturas a lo largo de la dirección perpendicular a la placa, en varios instantes. Se sugiere al lector probar con materiales de baja conductividad.

Ts=20; %temperatura ambiente
alfa=11352; %Coeficiente, 1/alfa del aluminio
L=0.5; % longitud placa
h1=10; %pérdidas por radiación
h2=10; %pérdidas por radiación
q_K=10000/209.3; %conductividad del aluminio

%raíces
x=linspace(0,30,10);
f=@(x) (h1*h2*L^2-x.^2).*sin(x)+(h1+h2)*L*x.*cos(x);
k=raices(f,x);

hold on
for t=[5 50 100 200]
    [x,T]=temperatura_10(Ts,L,h1,h2,q_K,k,alfa,t);
    plot(x,T,'displayName',num2str(t));
end
title('Evolución de la temperatura de la placa')
xlabel('x')
ylabel('T')
legend('-DynamicLegend','location','northeast')
grid on
hold off

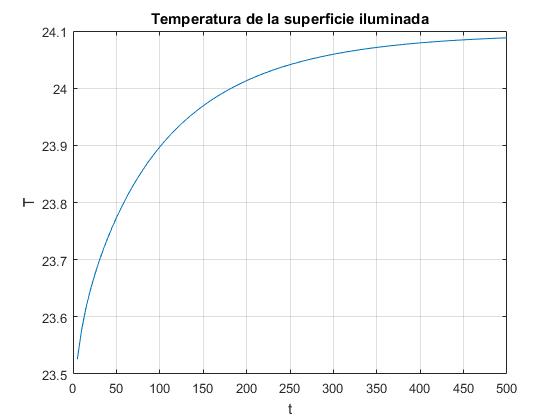
Creamos un script para mostrar la evolución de la temperatura de la superficie iluminada x=0, que tiende hacia un valor límite constante

Ts=20; %temperatura ambiente
alfa=11352; %Coeficiente, 1/alfa del aluminio
L=0.5; % longitud placa
h1=10; %pérdidas por radiación
h2=10; %pérdidas por radiación
q_K=10000/209.3; %conductividad del aluminio

%raíces
x=linspace(0,30,10);
f=@(x) (h1*h2*L^2-x.^2).*sin(x)+(h1+h2)*L*x.*cos(x);
k=raices(f,x);
t=5:5:500; %tiempo
T=zeros(1,length(t));
cte=q_K/(h1+h2+h1*h2*L);
for i=1:length(t)    
    T(i)=Ts+cte*(h2*L+1);
    for n=1:length(k)
        num=(-1/h1+h2*L^2/k(n)^2)*sin(k(n))+(h1+h2)*L*cos(k(n))/
(h1*k(n))-L*(h1+h2+h1*h2*L)/(h1*k(n));
        den=(1+k(n)^2)/(2*h1)+(k(n)/h1-L/k(n))*sin(2*k(n))/4-cos(2*k(n))
/(2*h1);
        T(i)=T(i)+(cte*num/den)*exp(-k(n)^2*t(i)/(alfa*L^2))*(k(n)/(h1*L));
    end
end
plot(t,T)

title('Temperatura de la superficie iluminada')
xlabel('t')
ylabel('T')
grid on

Una vez obtenidas las raíces k_n de la ecuación transcendente, comprobamos las relaciones de ortogonalidad entre las funciones X_n(x) y X_m(x) con m≠n

>> f1=@(x) cos(k(1)*x/L)+h1*L*sin(k(1)*x/L)/k(1);
>> f2=@(x) cos(k(2)*x/L)+h1*L*sin(k(2)*x/L)/k(2);
>> f3=@(x) f1(x).*f2(x);
>> integral(f3,0,L)
ans =   9.3675e-17

>> f1=@(x) cos(k(7)*x/L)+h1*L*sin(k(7)*x/L)/k(7);
>> f2=@(x) cos(k(5)*x/L)+h1*L*sin(k(5)*x/L)/k(5);
>> f3=@(x) f1(x).*f2(x);
>> integral(f3,0,L)
ans =   1.0408e-16

Nota

La primera raíz de la ecuación transcendente es k=0, esta raíz no está incluida por que produce divisiones entre cero o una indeterminación 0/0 al calcular los coeficientes B_n

Comprobamos con MATLAB que el coeficiente B es cero cuando k→0

>> syms k h1 h2 L;
>> num=(-1/h1+h2*L^2/k^2)*sin(k)+(h1+h2)*L*cos(k)/(h1*k)-
L*(h1+h2+h1*h2*L)/(h1*k);
>> den=(1+k^2)/(2*h1)+(k/h1-L/k)*sin(2*k)/4-cos(2*k)/(2*h1);
>> limit(num/den,k,0)
ans =0

Referencias

E Marín, A Lara-Bernal, A Calderón, O Delgado-Vasallo. On the heat transfer through a solid slab heated uniformly and continuously on one of its surfaces. Eur. J. Phys. 32 (2011) pp. 783-791