Vibración de una molécula diatómica.
El potencial de Lennard-Jones
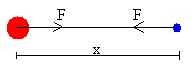
Dos átomos ligados formando una molécula estable tendrán una energía potencial Ep(x) que es una función cuadrática de la diferencia entre su separación x y la separación de equilibrio x0.
La fuerza F que describe la interacción entre los dos átomos está dirigida a lo largo de la línea que conecta los dos átomos y viene dada por
El movimiento de un sistema aislado de dos partículas se reduce al movimiento de una partícula de masa μ que se mueve alrededor de un centro fijo de fuerzas bajo la acción de la fuerza de interacción mutua.
donde μ es la masa reducida, es la aceleración relativa de la partícula de masa m1 respecto de la partícula de masa m2 y es la fuerza F(x) que describe la interacción mutua. En forma de ecuación diferencial
Esta es la ecuación diferencial de un Movimiento Armónico Simple de frecuencia angular
Ejemplo:
Determinar la constante k de fuerza de interacción entre los átomos de la molécula HCl sabiendo que su frecuencia de vibración f0=9·1013 Hz.
Datos: la masa del hidrógeno m1=1 y la masa del cloro m2=35 u.m.a. Una unidad de masa atómica (u.m.a.) vale 1.67·10-27 kg.
Teniendo en cuenta que ω0=2πf0, obtenemos k=519.2 N/m
Movimiento de los átomos
La solución de la ecuación diferencial es
x=x0+A·sin(ω0t+φ)
Donde x0 es la separación de equilibrio, A es la amplitud y φ la fase inicial que se determinan a partir de las condiciones iniciales, es decir, la posición x y la velocidad v en el instante t=0.
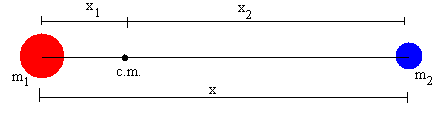
Determinamos el movimiento de cada una de las dos partículas, conocido el movimiento relativo de la partícula de masa m1 respecto de la partícula de masa m2 y suponiendo que el centro de masas de este sistema aislado está en reposo.
Actividades
En el programa interactivo se ha fijado el valor de k=2π2 y se permite variar las masas de los átomos m1 y m2 de la molécula diatómica.
Por ejemplo, cuando introducimos las masas de las moléculas m1=m2=1, la frecuencia angular de vibración vale ω0=2π y el periodo P=1 unidad de tiempo.
El "átomo" 1 se representa por un círculo de color rojo (a la izquierda), el "átomo" 2 por un círculo de color azul (a la derecha) y el centro de masas (en reposo) por un punto de color negro.
Una regla nos mide la distancia entre las dos partículas, y entre éstas y el c.m.
En la parte superior izquierda, se muestra el valor del tiempo (en unidades arbitrarias), que nos permite medir el periodo de las oscilaciones.
Ejemplo:
Si m1=2 y m2=1, la frecuencia angular y el periodo de las oscilaciones valen
El potencial de Lennard-Jones
La energía potencial Ep(r) de una molécula debida a las fuerzas intermoleculares es una función de r, la distancia entre los centros de las dos moléculas interactuantes. Esta función se puede expresar mediante una función conocida como potencial de Lennard-Jones.
El potencial de Lennard-Jones tiene una forma similar al potencial de Morse, una fórmula empírica que describe bastante bien la energía potencial del estado ligado de una molécula diatómica para una configuración electrónica dada.
Los parámetros r0 y E0 están determinados por la estructura de las moléculas individuales. Para r>r0 la pendiente de Ep(r) es positiva, la fuerza es atractiva, para r<r0, la pendiente es negativa y la fuerza es fuertemente repulsiva, mientras que para r=r0 la fuerza es nula (mínimo de la energía potencial).
Algunos valores típicos de r0 y E0 son los siguientes
| Gas | E0 (10-23 J) | r0 (angstroms) |
|---|---|---|
| Hidrógeno (H2) | 43 | 3.3 |
| Nitrógeno (N2) | 131 | 4.2 |
| Oxígeno (O2) | 162 | 3.9 |
Fuente: Roller, Blum. Physics, Mechanics, Waves and Thermodynamics. Edt. Holden-day (1981), pág. 655.
En la simulación vamos usar un potencial e(x) que es independiente de tipo de molécula, tomando x=r/r0.
La función e(x) se hace muy grande para valores de x menores que 1 y tiende hacia cero para valores grandes de x. El eje X es su asíntota horizontal. Para x=1 la función e(x) presenta un mínimo cuyo valor es -1.
Energía
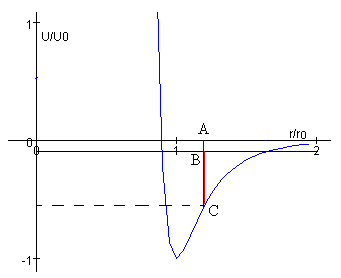
La energía total de la partícula en una posición x es la suma de la energía cinética y potencial
E=Ek+Ep(x)
En la figura, el segmento AB representa la energía total E, el segmento AC la energía potencial y el segmento BC la energía cinética.
Como la energía cinética no puede ser negativa, las abscisas de los dos puntos de intersección entre la recta horizontal (color negro) que señala la energía total constante E con la función Ep(x) (en color azul) marca los límites del movimiento de la partícula
La energía potencial es máxima en los dos puntos más alejados del equilibrio (x=1), y es mínima en la posición de equilibrio. Lo contrario le ocurre a la energía cinética que es cero en los dos puntos más alejados del origen y es máxima en x=1.
Fuerza
La fuerza sobre la partícula será
como vemos la posición de equilibrio f(x)=0 es x=1, que corresponde a un mínimo cuyo valor es -1.
A la izquierda de la posición de equilibrio x<1, la pendiente de la función Ep es negativa y su valor es muy grande (el ángulo es un poco más de 90º), la fuerza es positiva (hacia la derecha). A la derecha de la posición de equilibrio x>1, la pendiente de la curva es positiva y su valor es pequeño (próximo a cero para valores grandes de x), la fuerza es negativa (hacia la izquierda).
Ecuación del movimiento
La ecuación del movimiento de una partícula de masa m=1 es
Resolvemos esta ecuación diferencial por procedimientos numéricos para las siguientes condiciones iniciales.
En el instante t=0, la posición inicial de la partícula es x0 (a la derecha de la posición de equilibrio) y su velocidad inicial es v0=0. En la posición inicial, la energía cinética de la partícula es cero y por tanto, la energía potencial es igual a la energía total e.
Dada la energía total e de la partícula podemos hallar la posición inicial x0, para ello, hay que resolver la ecuación.
La raíz x0 de esta ecuación trascendente se calcula por procedimientos numéricos
e=-0.2; %energía total
g=@(x) e-1/x^12+2/x^6;
rMin=fzero(g,[0.5,1]);
rMax=fzero(g,[1,200]);
fprintf('Posiciones extremas [%1.3f, %1.3f]\n',rMin,rMax)
f=@(t,x) [x(2);12/x(1)^13-12/x(1)^7];
[t,x]=ode45(f,[0,4],[rMax,0]); %parte del reposo desde la posición rMax
plot(t,x(:,1))
grid on
xlabel('t')
ylabel('r/r_0');
title('Posición en función del tiempo')
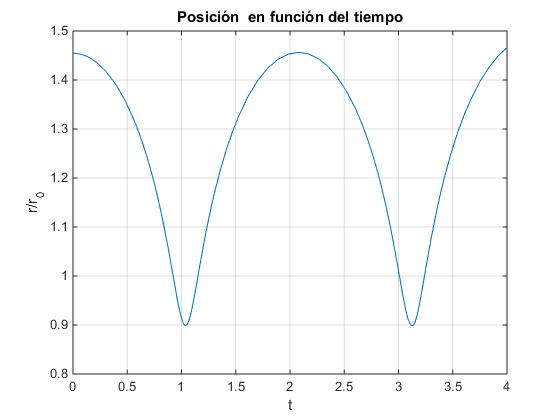
Posiciones extremas [0.899, 1.455]
Actividades
Se introduce un valor para la energía total de la partícula en el intervalo (-1, 0), en el control titulado Energía, se pulsa el botón titulado Nuevo
Observamos la representación de la función energía potencial e(x). Los valores de la energía cinética y potencial de la partícula representados por barras de color rojo y azul, respectivamente.

