El código para dibujar parte de la figura es (la explicación en el texto)

R=10; %radio
hold on
fplot(@(t) R*cos(t), @(t) R*sin(t),[0,2*pi]) %circunferencia
plot(0,0,'ko','markersize',3,'markerfacecolor','k')
line([-R,0],[R,R],'color','k') %línea AP
phi=pi/3; %posición de la placa
line([-R*sin(phi),-R*sin(phi)],[R,-R*cos(phi)],'lineStyle','--')
%placa M
line([-R*sin(phi)-cos(phi/4),-R*sin(phi)+cos(phi/4)],[-R*cos(phi)
+sin(phi/4),-R*cos(phi)-sin(phi/4)],'color','k')
line([-R*sin(phi),0],[-R*cos(phi),R],'lineStyle','--','color','k') %línea AM
%trayectoria
x=@(t) -R*sin(phi)+sqrt(9.8*R)*sin(th)*t;
y=@(t) -R*cos(phi)+2*sqrt(9.8*R)*cos(th/2)^2*t-4.9*t.^2;
fplot(x,y,[0,2*sqrt(R/9.8)])
hold off
axis square
axis off

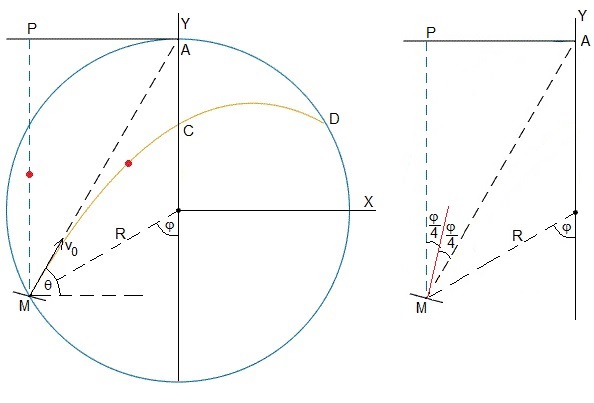
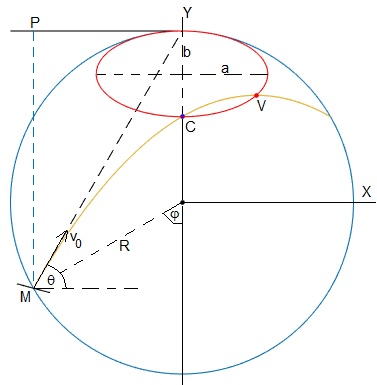
Sea una circunferencia vertical de radio R. Establecemos un Sistema de Referencia XY tal como se indica en la figura, el centro de la circunferencia es el origen.

Desde la posición P (-Rsinφ, R), se deja caer una partícula, que rebota elásticamente en la placa M cuyo centro está en la circunferencia, de modo que la dirección de su velocidad inicial v₀, después del choque, es la línea MA, o el ángulo de tiro θ. El choque se supone elástico, la orientación de la placa M es tal, que el ángulo que forma la normal a la placa con la dirección incidente PM (vertical), el igual al ángulo que forma MA (reflejado) con dicha normal

Movimiento rectilíneo

Sabiendo que la distancia PM es R+Rcosφ, la velocidad v₀ de la partícula cuando llega al punto M desde P (partiendo del reposo) es

${\displaystyle \begin{array}{l}R+R\cos \phi =\frac{1}{2}g{t}^2\\ v_0=gt=\sqrt{2gR\left(1+\cos \phi \right)}=2\sqrt{gR}\cos \left(\frac{\phi }{2}\right)\end{array}}$

Trayectoria parabólica

El ángulo de tiro θ es

${\displaystyle \tan \theta =\frac{R+R\cos \phi }{R\sin \phi }}$

Empleando las relaciones trigonométricas del seno y coseno con la tangente, relacionamos el ángulo de tiro θ con el ángulo φ de posición del centro de la placa M medido desde el eje -Y

${\displaystyle \begin{array}{l}\sin \theta =\frac{\tan \theta }{\sqrt{1+{\tan }^2\theta }}=\cos \frac{\phi }{2},\cos \theta =\frac{1}{\sqrt{1+{\tan }^2\theta }}=\sin \frac{\phi }{2}\\ \theta =\frac{\pi }{2}-\frac{\phi }{2}\end{array}}$

La partícula parte de M en el instante t=0, con velocidad v₀ y ángulo de tiro θ. Las ecuaciones del movimiento son

${\displaystyle \begin{array}{l}\{\begin{array}{l}{a}_x=0\\ a_y=-g\end{array}\{\begin{array}{l}{v}_x=v_0\cos \theta \\ v_y=v_0\sin \theta -gt\end{array}\{\begin{array}{l}x=-R\sin \phi +v_0\cos \theta ·t\\ y=-R\cos \phi +v_0\sin \theta ·t-\frac{1}{2}g{t}^2\end{array}\\ \{\begin{array}{l}x=-R\sin \phi +\sqrt{gR}\sin \phi ·t\\ y=-R\cos \phi +2\sqrt{gR}{\cos }^2\left(\frac{\phi }{2}\right)·t-\frac{1}{2}g{t}^2\end{array}\end{array}}$

Intersección de la trayectoria con el eje Y

La trayectoria corta al eje Y en un punto C (0, y₁) y emplea un tiempo t₁ en alcanzarlo

${\displaystyle \begin{array}{l}0=-R\sin \phi +\sqrt{gR}\sin \phi ·t_1\\ t_1=\sqrt{\frac{R}{g}}\end{array}}$

Todas las partículas emplean el mismo tiempo en alcanzar el eje vertical Y, ya que t₁ es independiente de φ

${\displaystyle \begin{array}{l}{y}_1=-R\cos \phi +2\sqrt{gR}{\cos }^2\left(\frac{\phi }{2}\right)·t_1-\frac{1}{2}g{t}_1^2\\ y_1=-R\cos \phi +2\sqrt{gR}{\cos }^2\left(\frac{\phi }{2}\right)\sqrt{\frac{R}{g}}-\frac{1}{2}g\frac{R}{g}=\frac{R}{2}\end{array}}$

Todas las trayectorias cortan al eje Y en el punto C (0,R/2), véase la figura más abajo

Casos particulares

Estudiamos la trayectoria de las partículas que rebotan sobre las placas M situadas en los extremos del tercer cuadrante

• Cuando φ=π/2

${\displaystyle \begin{array}{l}\{\begin{array}{l}x=-R+\sqrt{gR}·t\\ y=\sqrt{gR}·t-\frac{1}{2}g{t}^2\end{array}\\ y=-\frac{x^2}{2R}+\frac{R}{2}\end{array}}$

Para x=0, y=R/2, pasa por el punto C empleando un tiempo t₁

${\displaystyle 0=-R+\sqrt{gR}·t,t_1=\frac{R}{\sqrt{gR}}=\sqrt{\frac{R}{g}}}$

Para x=R, y=0, empleando un tiempo t₂ en llegar al otro extremo del diámetro horizontal

${\displaystyle \begin{array}{l}R=-R+\sqrt{gR}·t_2\\ t_2=2\sqrt{\frac{R}{g}}\end{array}}$

Al ser la trayectoria simétrica t₂ es el doble de t₁

• Cuando φ=0

${\displaystyle \{\begin{array}{l}x=0\\ y=-R+2\sqrt{gR}·t-\frac{1}{2}g{t}^2\end{array}}$

La partícula se mueve a lo largo del eje vertical Y partiendo de la posición M (0,-R). Alcanza el punto C (0, R/2) en el instante t₁

${\displaystyle \begin{array}{l}\frac{R}{2}=-R+2\sqrt{gR}·t_1-\frac{1}{2}g{t}_1^2\\ t_1=\sqrt{\frac{R}{g}}\end{array}}$

Alcanza la altura máxima cuando v_y=0, en el instante t₂.

${\displaystyle \begin{array}{l}{t}_2=\frac{v_0\sin \theta }{g}=\frac{2\sqrt{gR}{\cos }^2\left(\frac{\phi }{2}\right)}{g}\\ \phi =\mathrm{0,}{t}_2=2\sqrt{\frac{R}{g}},y=R\end{array}}$

La posición final de la partícula en el instante t₂ es y=R como cabría esperar de una partícula que se deja caer desde el punto P (0,R) y rebota elásticamente en la placa situada en M (0, -R)

Representamos las trayectorias de las partículas que rebotan en las placas M situadas en los ángulos φ: 0,10,20,...90°, entre los instantes t=0 y t=t₂

R=10; %radio
hold on
fplot(@(t) R*cos(t), @(t) R*sin(t),[0,2*pi])
line([-R,0],[R,R])
for phi=(0:10:90)*pi/180
    x=@(t) -R*sin(phi)+sqrt(9.8*R)*sin(phi)*t;
    y=@(t) -R*cos(phi)+2*sqrt(9.8*R)*cos(phi/2)^2*t-4.9*t.^2;
    fplot(x,y,[0,2*sqrt(R/9.8)])
end
hold off
grid on
axis square
xlabel('x')
ylabel('y')
title('Tiro parabólico')

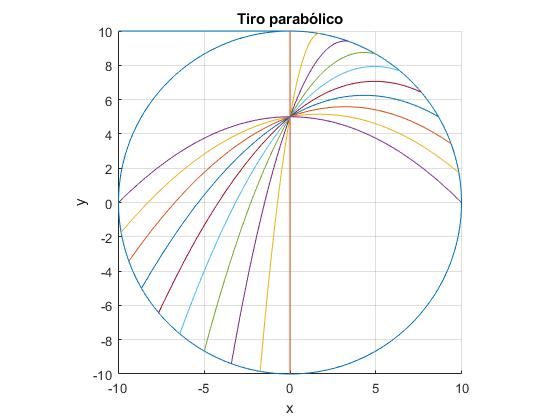
Observamos que todas las tayectorias se cruzan en el punto C (0, R/2) empleando un tiempo $t_1=\sqrt{\frac{R}{g}}$ . La intersección de las trayectorias parabólicas con la circunferencia de radio R se produce en el instante t₂ que es el doble de t₁. Lo que aparentemente resulta curioso

Intersección de la trayectoria con la circunferencia de radio R

La ecuación de la circunferencia de radio R centrada en el origen es

${\displaystyle \begin{array}{l}{x}^2+y^2=R^2\\ {\left(-R\sin \phi +\sqrt{gR}\sin \phi ·t\right)}^2+{\left(-R\cos \phi +2\sqrt{gR}{\cos }^2\left(\frac{\phi }{2}\right)·t-\frac{1}{2}g{t}^2\right)}^2=R^2\end{array}}$

Haciendo operaciones obtenemos una ecuación de tercer grado en t

${\displaystyle t^3+a{t}^2+bt+c=0\{\begin{array}{l}a=-8\sqrt{\frac{R}{g}}{\cos }^2\left(\frac{\phi }{2}\right)\\ b=4\frac{R}{g}\left({\sin }^2\phi +4{\cos }^2\left(\frac{\phi }{2}\right)+\cos \phi \right)\\ c=-8{\left(\frac{R}{g}\right)}^{3/2}\left({\sin }^2\phi +2\cos \phi {\cos }^2\left(\frac{\phi }{2}\right)\right)\end{array}}$

Comprobamos que obtenemos el mismo tiempo $t_2=2\sqrt{\frac{R}{g}}$, cualquiera que sea el ángulo φ (30, 45, 60°)

R=10; %radio
for phi=pi/6:pi/12:pi/3
    a=-8*sqrt(R/9.8)*cos(phi/2)^2;
    b=(cos(phi)+4*cos(phi/2)^4+sin(phi)^2)*4*R/9.8;
    c=-(sin(phi)^2+2*cos(phi)*cos(phi/2)^2)*8*sqrt(R/9.8)*R/9.8;
    raiz=raices_3([1,a,b,c])
    disp(raiz)
end

   2.0203
   2.7598
   2.7598

   2.0203 + 0.0000i
   2.4387 - 1.0102i
   2.4387 + 1.0102i

   2.0203 + 0.0000i
   2.0203 + 1.4286i
   2.0203 - 1.4286i

>> 2*sqrt(R/9.8)
ans =    2.0203

Empleamos la función raices_3 para calcular las raíces de una ecuación cúbica, alternativamente, se puede utilizar la función roots de MATLAB

El lugar geométrico de los vértices

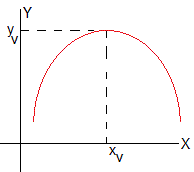
La ecuación de la parábola es, y=ax²+bx+c. Si a<0, el vértice es un máximo de coordenadas (x_v, y_v)

${\displaystyle \begin{array}{l}\frac{dy}{dx}=2ax+b=\mathrm{0,}{x}_v=-\frac{b}{2a}\\ y_v=a{\left(-\frac{b}{2a}\right)}^2+b\left(-\frac{b}{2a}\right)+c=c-\frac{b^2}{4a}\end{array}}$

En el apartado anterior, hemos obtenido las ecuaciones paramétricas de la trayectoria, despejamos el tiempo t de la primera y lo introducimos en la segunda para obtener la función y=y(x)

${\displaystyle \begin{array}{l}y=-R\cos \phi +2\sqrt{gR}{\cos }^2\left(\frac{\phi }{2}\right)\left(\frac{x+R\sin \phi }{\sqrt{gR}\sin \phi }\right)-\frac{1}{2}g{\left(\frac{x+R\sin \phi }{\sqrt{gR}\sin \phi }\right)}^2=\\ y=-\frac{1}{2}\frac{x^2}{R{\sin }^2\phi }+\left(2{\cos }^2\left(\frac{\phi }{2}\right)-1\right)\frac{x}{\sin \phi }-R\cos \phi -\frac{1}{2}R\\ y=-\frac{1}{2}\frac{x^2}{R{\sin }^2\phi }+\frac{\cos \phi }{\sin \phi }x-R\cos \phi -\frac{1}{2}R+2R{\cos }^2\left(\frac{\phi }{2}\right)\end{array}}$

Las coordenadas del vértice son

${\displaystyle \begin{array}{l}a=-\frac{1}{2R{\sin }^2\phi },b=\frac{\cos \phi }{\sin \phi },c=-R\cos \phi -\frac{1}{2}R+2R{\cos }^2\left(\frac{\phi }{2}\right)\\ x_v=R\sin \phi \cos \phi ,y_v=-R\cos \phi +2R{\cos }^2\left(\frac{\phi }{2}\right)-\frac{R}{2}{\sin }^2\phi \end{array}}$

En la figura, se señalan los vértices de las trayectorias parabólicas mediante puntos de color rojo

R=10; %radio
hold on
fplot(@(t) R*cos(t), @(t) R*sin(t),[0,2*pi])
line([-R,0],[R,R])
for phi=(0:10:90)*pi/180
     x=@(t) -R*sin(phi)+sqrt(9.8*R)*sin(phi)*t;
     y=@(t) -R*cos(phi)+2*sqrt(9.8*R)*cos(phi/2)^2*t-4.9*t.^2;
     fplot(x,y,[0,2*sqrt(R/9.8)])
     xV=R*sin(phi)*cos(phi); %vértices
     yV=-R*cos(phi)+2*R*cos(phi/2)^2-R*sin(phi)^2/2;
     plot(xV,yV,'ro','markersize',3,'markerfacecolor','r')
end
hold off
grid on
axis square
xlabel('x')
ylabel('y')
title('Vértices')

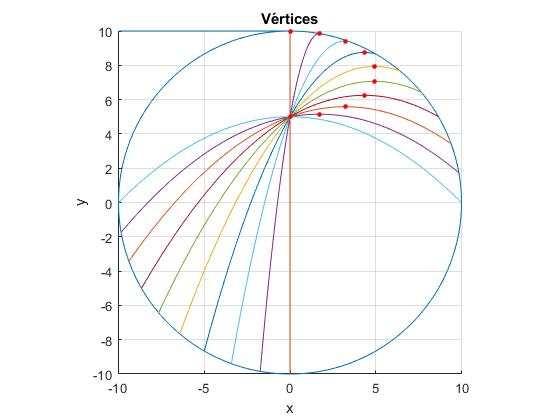
Vamos a comprobar que el lugar geométrico de los vértices es una elipse centrada en la posición (0, 3R/4) de semieje menor b=R/4. Calcularemos el semieje mayor a a partir de la ecuación de la elipse

${\displaystyle \frac{x_v^2}{a^2}+\frac{{\left(y_v-\frac{3}{4}R\right)}^2}{{\left(\frac{R}{4}\right)}^2}=1}$

Despejamos a² y utilizaremos Math Symbolic de MATLAB para realizar las operaciones algebraicas

>> syms R phi;
>> x=R*sin(phi)*cos(phi);
>> y=-R*cos(phi)+2*R*cos(phi/2)^2-R*sin(phi)^2/2;
>> a2=x^2/(1-16*(y-3*R/4)^2/R^2);
>> simplify(a2)
ans =R^2/4

El resultado es

${\displaystyle a^2=\frac{R^2}{4},a=\frac{R}{2}}$

El lugar geométrico de los focos

Sea la parábola de ecuación, $y=-\frac{1}{4p}{x}^2$. El vértice está en el origen (0,0) y el foco, a una distancia p por debajo tal como se aprecia en la figura de la izquierda

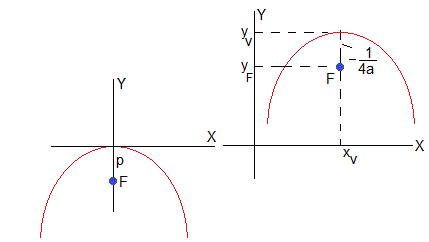
Sea una parábola de ecuación y=ax²+bx+c, con a<0. Las coordenadas del foco son

${\displaystyle \begin{array}{l}{x}_F=-\frac{b}{2a},y_F=c-\frac{b^2}{4a}+\frac{1}{4a},a<0\\ x_F=R\sin \phi \cos \phi ,y_F=-R\cos \phi -\frac{R}{2}+2R{\cos }^2\left(\frac{\phi }{2}\right)+\frac{R}{2}\cos \left(2\phi \right)\end{array}}$

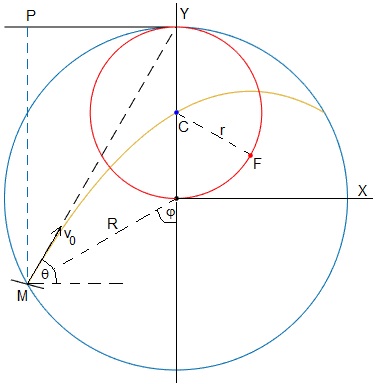
Comprobamos que el lugar geométrico de los focos es una circunferencia centrada en el punto (0, R/2) cuyo radio r vamos a determinar con ayuda de Math Symbolic de MATLAB

${\displaystyle x_F^2+{\left(y_F^2-\frac{R}{2}\right)}^2=r^2}$

>> syms R phi;
>> xF=R*sin(phi)*cos(phi);
>> yF=-R*cos(phi)-R/2+2*R*cos(phi/2)^2+R*cos(2*phi)/2;
>> simplify((xF^2+(yF-R/2)^2)
ans =R^2/4

Se trata de una circunferencia de radio r=R/2

La envolvente

La ecuación de la trayectoria depende del ángulo φ, f(x, y, φ)=0

${\displaystyle y=-\frac{1}{2}\frac{x^2}{R{\sin }^2\phi }+\frac{\cos \phi }{\sin \phi }x-R\cos \phi -\frac{1}{2}R+2R{\cos }^2\left(\frac{\phi }{2}\right)}$

Se obtiene la ecuación de la envolvente de las trayectorias derivando con respecto a φ e igualando a cero.

${\displaystyle \begin{array}{l}\frac{\partial f}{\partial \phi }=0\\ \frac{x^2}{R}\frac{\cos \phi }{{\sin }^3\phi }-\frac{x}{{\sin }^2\phi }=0\\ \tan \phi =\frac{x}{R}\end{array}}$

Combinamos esta ecuación con la de la trayectoria para eliminar el ángulo φ y así obtener la ecuación de la envolvente. Para ello, utilizamos las relaciones trigonométricas

${\displaystyle \begin{array}{l}\sin \phi =\frac{\tan \phi }{\sqrt{1+{\tan }^2\phi }}=\frac{\frac{x}{R}}{\sqrt{1+\frac{x^2}{R^2}}}=\frac{x}{\sqrt{x^2+R^2}},\cos \phi =\frac{1}{\sqrt{1+{\tan }^2\phi }}=\frac{R}{\sqrt{x^2+R^2}}\\ \tan \phi =\frac{2\tan \left(\frac{\phi }{2}\right)}{1-{\tan }^2\left(\frac{\phi }{2}\right)},\tan \left(\frac{\phi }{2}\right)=-\frac{R}{x}+\sqrt{\frac{R^2}{x^2}+1}=\frac{1}{x}\left(-R+\sqrt{x^2+R^2}\right)\end{array}}$

La ecuación de la envolvente es

${\displaystyle y=-\frac{x^2}{2R}-\frac{R^2}{\sqrt{x^2+R^2}}+\frac{2R{x}^2}{x^2+{\left(-R+\sqrt{x^2+R^2}\right)}^2}}$

R=10; %radio
hold on
fplot(@(t) R*cos(t), @(t) R*sin(t),[0,2*pi])
line([-R,0],[R,R])
for phi=(0:10:90)*pi/180
%trayectoria    
    y=@(x) -x.^2/(2*R*sin(phi)^2)+cos(phi)*x/sin(phi)-R*cos(phi)-
R/2+2*R*cos(phi/2)^2;
    fplot(y,[-R*sin(phi),2*R])
end
%envolvente
yy=@(x) -x.^2/(2*R)-R^2./sqrt(R^2+x.^2)+2*R*x.^2./
(x.^2+(-R+sqrt(x.^2+R^2)).^2); 
fplot(yy,[0,2*R],'color','k')
hold off
grid on
axis square
xlim([-R,2*R])
ylim([-R,2*R])
xlabel('x')
ylabel('y')
title('Envolvente')

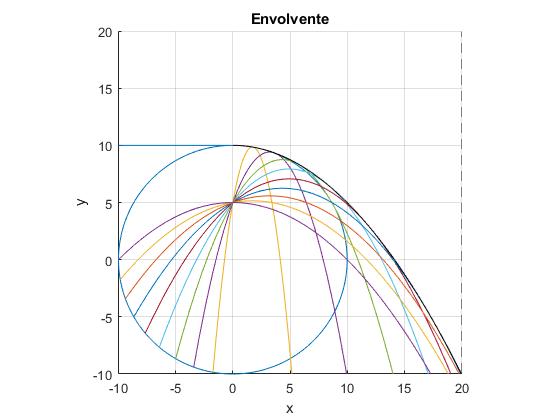
La envolvente es la línea de color negro

Referencias

Radhakrishnamurty Padyala. A Hidden Circle in a Family of Projectile Paths. The Physics Teacher. Vol.58, February 2020, pp. 116-118