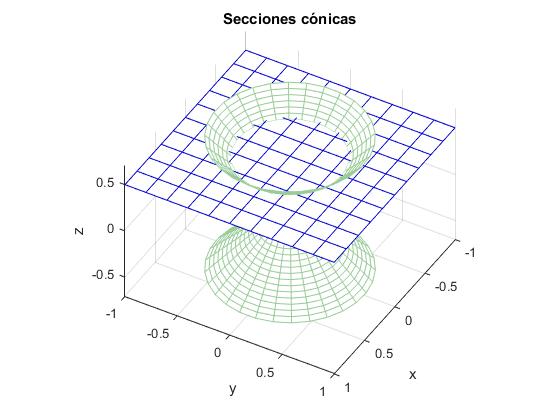
Secciones cónicas
Las secciones cónicas (elipse, hipérbola y parábola) es el resultado de la intersección de una superficie cónica y un plano
Circunferencia
%superficie cónica
theta=pi/4;
r=linspace(-1,1,40);
phi=linspace(0,2*pi,30);
[r,phi]=meshgrid(r,phi);
x=r.*cos(phi)*sin(theta);
y=r.*sin(phi)*sin(theta);
z=r*cos(theta);
h1=mesh(x,y,z);
set(h1,'EdgeColor',[0.6,0.8,0.6])
%plano horizontal
[x,y]=meshgrid(-1:0.2:1);
z=0.5*ones(size(x));
hold on
h1=mesh(x,y,z);
set(h1,'EdgeColor',[0,0,0.8])
axis equal
view(120,40)
hold off
xlabel('x'); ylabel('y'); zlabel('z')
title('Secciones cónicas')
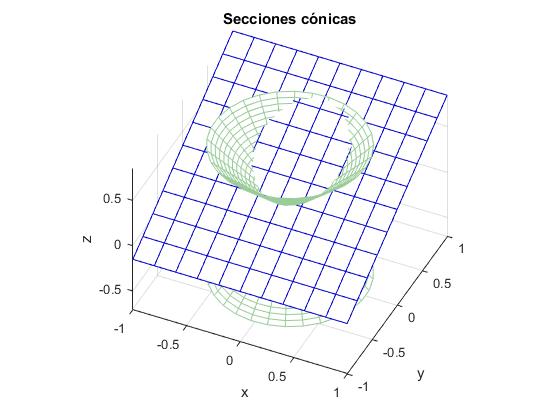
Elipse
%superficie cónica
theta=pi/4;
r=linspace(-1,1,40);
phi=linspace(0,2*pi,30);
[r,phi]=meshgrid(r,phi);
x=r.*cos(phi)*sin(theta);
y=r.*sin(phi)*sin(theta);
z=r*cos(theta);
h1=mesh(x,y,z);
set(h1,'EdgeColor',[0.6,0.8,0.6])
%plano inclinado
[x,y]=meshgrid(-1:0.2:1);
z=0.5*y+0.35; % probar, z=y+0.35;
hold on
h1=mesh(x,y,z);
set(h1,'EdgeColor',[0,0,0.8])
axis equal
view(25,40)
hold off
xlabel('x'); ylabel('y'); zlabel('z')
title('Secciones cónicas')
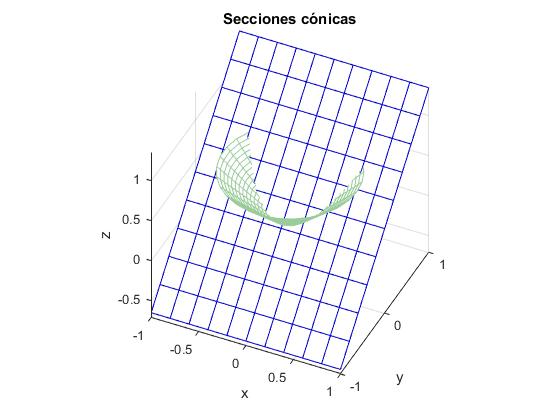
Parábola
%superficie cónica
theta=pi/4;
r=linspace(-1,1,40);
phi=linspace(0,2*pi,30);
[r,phi]=meshgrid(r,phi);
x=r.*cos(phi)*sin(theta);
y=r.*sin(phi)*sin(theta);
z=r*cos(theta);
h1=mesh(x,y,z);
set(h1,'EdgeColor',[0.6,0.8,0.6])
%plano inclinado
[x,y]=meshgrid(-1:0.2:1);
z=y+0.35; %z=0.5*y+0.35;
hold on
h1=mesh(x,y,z);
set(h1,'EdgeColor',[0,0,0.8])
axis equal
view(25,40)
hold off
xlabel('x'); ylabel('y'); zlabel('z')
title('Secciones cónicas')
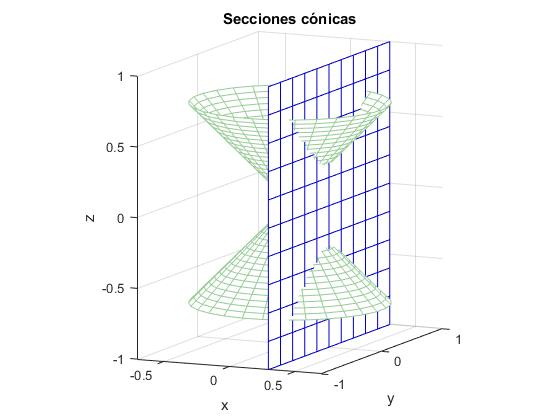
Hipérbola
%superficie cónica
theta=pi/4;
r=linspace(-1,1,40);
phi=linspace(0,2*pi,30);
[r,phi]=meshgrid(r,phi);
x=r.*cos(phi)*sin(theta);
y=r.*sin(phi)*sin(theta);
z=r*cos(theta);
h1=mesh(x,y,z);
set(h1,'EdgeColor',[0.6,0.8,0.6])
%plano vertical
[y,z]=meshgrid(-1:0.2:1);
x=0.3*ones(size(y));
hold on
h1=mesh(x,y,z);
set(h1,'EdgeColor',[0,0,0.8])
axis equal
view(25,10)
hold off
xlabel('x'); ylabel('y'); zlabel('z')
title('Secciones cónicas')
La parábola
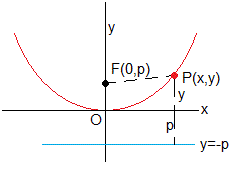
Esta parábola es un conjunto de puntos P(x,y) del plano que son equidistantes de un punto fijo F(0,p) denominado foco y de una línea fija, paralela al eje x, y=-p, denominada directriz
La distancia entre el punto P y el foco F es
La distancia entre el punto P y la directriz es y+p. La figura muestra el caso en el que p>0
Ecuación de la parábola
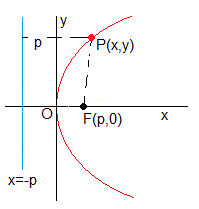
Esta parábola es un conjunto de puntos P(x,y) del plano que son equidistantes de un punto fijo F(0,p) denominado foco y de una línea fija, paralela al eje y, x=-p, denominada directriz
La ecuación de la parábola es
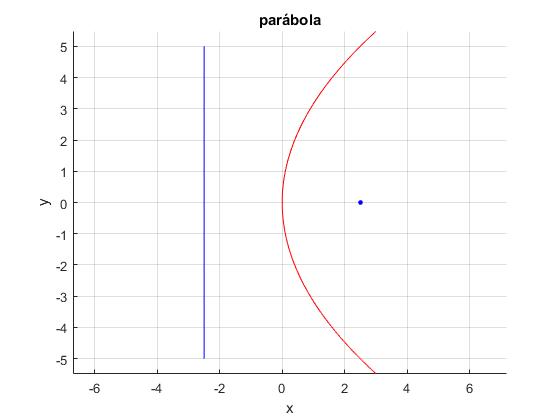
Representamos la parábola y2=10x. El parámetro p=10/4=5/2. El foco está en el punto F(5/2,0) y la directriz es la recta x=-5/2
f=@(x) sqrt(10*x);
g=@(x) -f(x);
hold on
fplot(f,[0,3],'r')
fplot(g,[-0,3],'r')
plot(5/2,0,'bo','markersize',3,'markeredgecolor','b','markerfacecolor','b')
line([-5/2,-5/2],[-5,5], 'color','b') %directriz
hold off
grid on
axis equal
xlabel('x')
ylabel('y')
title('parábola')
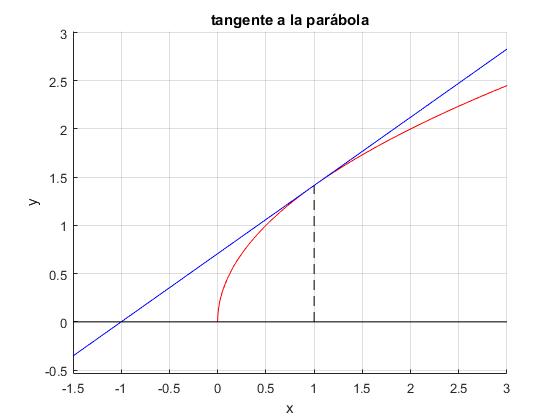
Tangente a la parábola
Calculamos la ecuación de la recta tangente a la parábola y2=4px en el punto (x1, y1)
La pendiente m de la recta tangente es
La recta de pendiente m pasa por el punto (x1, y1)
Corta al eje X en el punto (-x1,0)
p=0.5;
f=@(x) 2*sqrt(p*x);
hold on
fplot(f,[0,3], 'r')
x1=1; y1=f(x1);
m=2*p/y1;
g=@(x) m*(x-x1)+y1;
fplot(g,[-1.5,3],'b');
line([x1,x1],[0,y1],'color','k','linestyle','--')
line([-1.5,3],[0,0],'color','k') %eje X
hold off
grid on
axis equal
xlabel('x')
ylabel('y')
title('tangente a la parábola')
Elipse
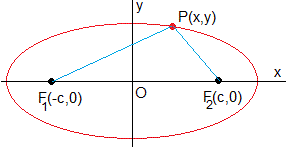
Una elipse es el conjunto de puntos P(x,y) del plano tal que la suma de las distancias a dos puntos fijos F1(-c,0) y F2(c,0) es constante e igual a 2a>0.
Situamos los focos F1 y F2 de la elipse en el eje X que es la recta que pasa por los puntos (-c,0) y (c,0), de modo que el origen O está entre los focos, en la mitad. La ecuación de la elipse es
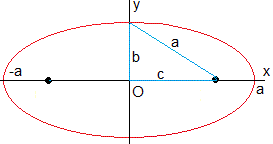
SE calculan las intersecciones con el eje X, haciendo y=0, x2=a2, x=±a. Los puntos (-a,0) y (a,0) se llaman vértices de la elipse y el segmento que los une, eje mayor 2a de la elipse. 2b se denomina eje menor de la elipse
En la figura, vemos que la relación existente entre a, b y c es a2=b2+c2
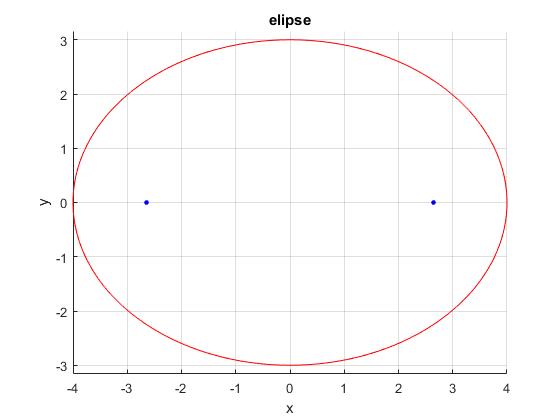
Representamos la siguiente elipse, señalando la posición de sus focos
a=4; %semieje mayor
b=3; %semieje menor
c=sqrt(a^2-b^2); %semistancia focal
f=@(x) b*sqrt(a^2-x.^2)/a;
g=@(x) -f(x);
hold on
fplot(f,[-a,a],'r')
fplot(g,[-a,a],'r')
plot([-c,c],[0,0],'bo','markersize',3,'markeredgecolor','b','markerfacecolor','b')
hold off
grid on
axis equal
xlabel('x')
ylabel('y')
title('elipse')
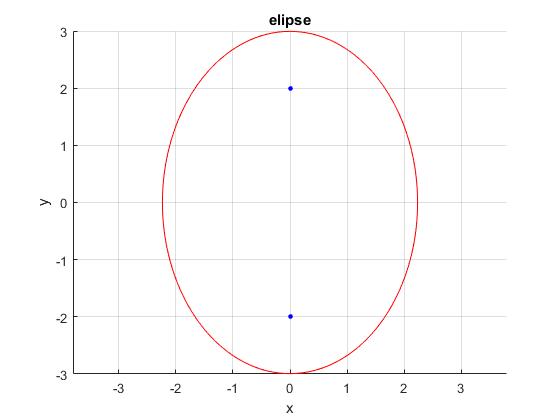
Representamos ahora la elipse, señalando la posición de sus focos
a=sqrt(5);
b=3;
c=sqrt(b^2-a^2);
f=@(x) b*sqrt(a^2-x.^2)/a;
g=@(x) -f(x);
hold on
fplot(f,[-a,a],'r')
fplot(g,[-a,a],'r')
plot([0,0],[c,-c],'bo','markersize',3,'markeredgecolor','b','markerfacecolor','b')
hold off
grid on
axis equal
xlabel('x')
ylabel('y')
title('elipse')
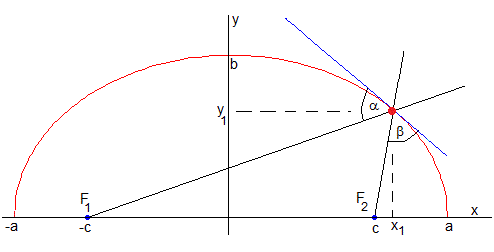
Tangente a la elipse
Vamos a demostrar que los ángulos α y β son iguales, por lo que la luz o el sonido procedente de del foco F1 se refleja en un punto P de la elipse y pasa por el foco F2.
Para dibujar la elipse y su tangente se ha empleado el siguiente código
b=3;
a=4;
c=sqrt(a^2-b^2);
f=@(x) b*sqrt(a^2-x.^2)/a;
hold on
fplot(f,[-a,a], 'r')
x1=3; y1=f(x1);
line([-c,x1],[0,y1],'color','k');
line([c,x1],[0,y1],'color','k');
line([-a,a],[0,0],'color','k') %eje X
m=-b^2*x1/(a^2*y1);
g=@(x) m*(x-x1)+y1;
fplot(g,[1,4],'b');
plot([-c,c],[0,0],'bo','markersize',3,'markeredgecolor','b','markerfacecolor','b')
hold off
grid on
axis equal
xlabel('x')
ylabel('y')
title('tangente a la elipse')
La pendiente de la recta tangente (en color azul) a la elipse en el punto (x1, y1) es
La pendiente de la recta que pasa por el foco F1 y el punto P(x1, y1) es
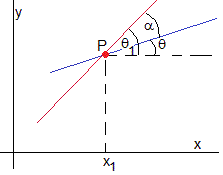
El ángulo α entre las dos rectas que pasan por P es la diferencia θ1-θ
Hemos utilizado la ecuación de la elipse para relacionar x1 con y1
La pendiente de la recta que pasa por el foco F2 y el punto P(x1, y1) es
El ángulo β es el suplementario de la diferencia θ2-θ
Los ángulos α y β son iguales, ya que tan(θ2-θ)=tan(180-β)=-tanβ
Hipérbola
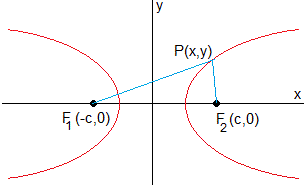
Una hipérbola es el conjunto de puntos P(x,y) del plano tal que la diferencia de las distancias a dos puntos fijos F1(-c,0) y F2(c,0) es constante e igual a ±2a>0.
Donde c2=a2+b2
Se calcula la intersección con el eje X, haciendo y=0, x=±a, que son los vértices de la hipérbola. No hay intersecciones con el eje Y, ya que cuando x=0, x2=-b2, que no tiene solución real.
Despejamos y en la ecuación de la hipérbola
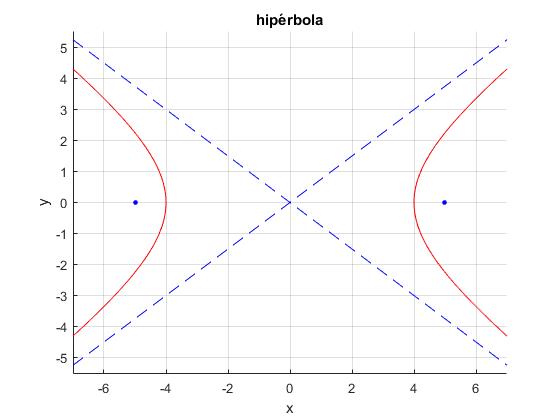
Cuando x se hace grande y tiende hacia y=±(b/a)x, que son las asíntotas de la hipérbola. Dibujamos los focos, los vértices y las asíntotas de la hipérbola
a=4;
b=3;
c=sqrt(a^2+b^2);
f=@(x) b*sqrt(x.^2-a^2)/a;
g=@(x) -f(x);
hold on
fplot(f,[4,7],'r')
fplot(g,[4,7],'r')
fplot(f,[-7,-4],'r')
fplot(g,[-7,-4],'r')
%focos
plot([-c,c],[0,0],'bo','markersize',3,'markeredgecolor','b','markerfacecolor','b')
f=@(x) b*x/a;
line([-7,7],[f(-7),f(7)], 'color','b','linestyle','--') %asíntota
line([-7,7],[-f(-7),-f(7)], 'color','b', 'linestyle','--') %asíntota
hold off
grid on
axis equal
xlabel('x')
ylabel('y')
title('hipérbola')
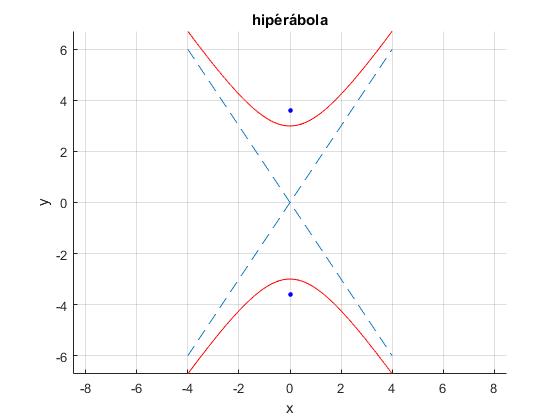
Dibujamos la hipérbola, sus focos y asíntotas
a=2;
b=3;
c=sqrt(a^2+b^2);
f=@(x) b*sqrt(a^2+x.^2)/a;
g=@(x) -f(x);
hold on
fplot(f,[-4,4],'r')
fplot(g,[-4,4],'r')
plot([0,0],[c,-c],'bo','markersize',3,'markeredgecolor','b','markerfacecolor','b')
f=@(x) b*x/a;
line([-4,4],[f(-4),f(4)], 'linestyle','--') %asíntota
line([-4,4],[-f(-4),-f(4)], 'linestyle','--') %asíntota
hold off
grid on
axis equal
xlabel('x')
ylabel('y')
title('hipérábola')
Tangente a la hipérbola
Vamos a demostrar que los ángulos α y β son iguales, del mismo modo que se hizo para la elipse.
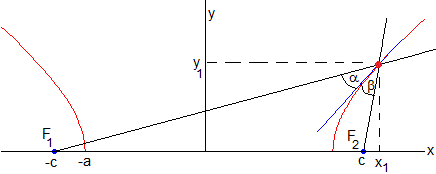
La pendiente de la recta tangente (en color azul) a la hipérbola en el punto (x1, y1) es
La pendiente de la recta que pasa por el foco F1 y el punto P(x1, y1) es
El ángulo α entre las dos rectas que pasan por P es la diferencia θ-θ1
Hemos utilizado la ecuación de la hipérbola para relacionar x1 con y1
La pendiente de la recta que pasa por el foco F2 y el punto P(x1, y1) es
El ángulo β es la diferencia θ2-θ
Los ángulos α y β son iguales. Un rayo de luz que incida en un espejo hipérbólico en P y cuya dirección pase por el foco F2, se refleja y pasa por el foco F1 tal como se aprecia en la figura.

Cónicas centradas en otro punto distinto del origen
Las cónicas no tienen que estar centradas en el origen, pueden estar en otros puntos
Parábola
Sea la ecuación de la parábola
x0=-2; %centro
y0=3;
p=2;
f=@(x) (x-x0).^2/(4*p)+y0;
hold on
fplot(f,[-5,1],'r')
plot(x0,y0+p,'bo','markersize',3,'markeredgecolor','b',
'markerfacecolor','b')
line([-5,1],[y0-p,y0-p], 'color','b') %directriz
hold off
grid on
ylim([0,5])
axis equal
xlabel('x')
ylabel('y')
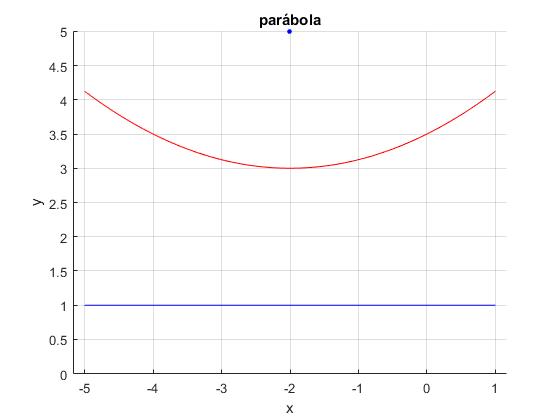
title('parábola')
Se trata de una parábola centrada en el punto (-2,3), el parámetro 4p=8, por lo que p=2. Representamos la parábola, su foco y directriz
Elipse
Sea la ecuación de la elipse
Completamos cuadrados
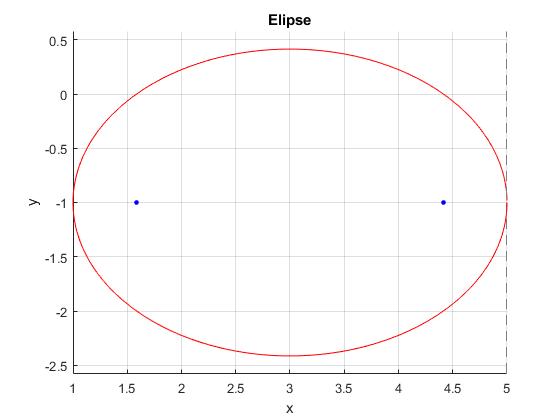
Se trata de una elipse centrada en el punto (3,-1). Representamos la elipse y sus focos
x0=3; %centro
y0=-1;
a=2;
b=sqrt(2);
c=sqrt(a^2-b^2);
f=@(x) y0+b*sqrt(a^2-(x-x0).^2)/a;
g=@(x) y0-b*sqrt(a^2-(x-x0).^2)/a;
hold on
fplot(f,[1,5],'r')
fplot(g,[1,5],'r')
%focos
plot([x0+c,x0-c],[y0,y0],'bo','markersize',3,'markeredgecolor',
'b','markerfacecolor','b')
hold off
grid on
axis equal
xlabel('x')
ylabel('y')
title('Elipse')
Hipérbola
Sea la ecuación de la hipérbola
Completamos cuadrados
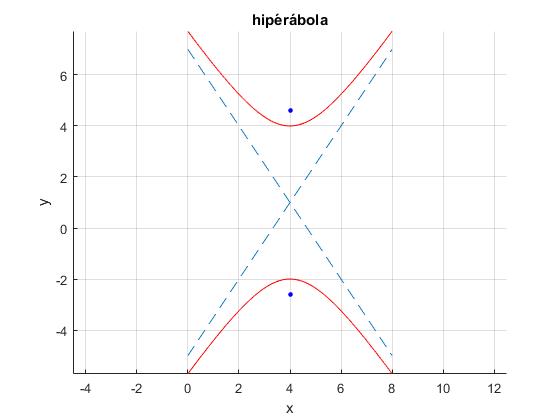
Se trata de una hipérbola centrada en el punto (4,1). Representamos la hipérbola, sus focos y asíntotas
x0=4; %centro
y0=1;
a=2;
b=3;
c=sqrt(a^2+b^2);
f=@(x) y0+b*sqrt(a^2+(x-x0).^2)/a;
g=@(x) y0-b*sqrt(a^2+(x-x0).^2)/a;
hold on
fplot(f,[0,8],'r')
fplot(g,[0,8],'r')
%focos
plot([x0,x0],[y0+c,y0-c],'bo','markersize',3,'markeredgecolor',
'b','markerfacecolor','b')
f=@(x) b*(x-x0)/a+y0;
g=@(x) -b*(x-x0)/a+y0;
line([0,8],[f(0),f(8)], 'linestyle','--') %asíntota
line([0,8],[g(0),g(8)], 'linestyle','--') %asíntota
hold off
grid on
axis equal
xlabel('x')
ylabel('y')
title('hipérbola')
Ecuación general de una cónica
Que se analiza en un sistema de referencia girado OXY en el que se elimina el término en B en xy.
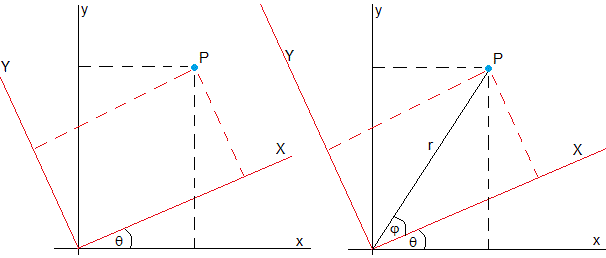
Las coordenadas del punto P en el sistema de referencia Oxy son (x,y). Las coordenadas del punto P en el sistema de referencia OXY girado un ángulo θ son (X,Y). Vamos a relacionar x e y con X e Y
Sea r la distancia entre el origen O y el punto P y φ el ángulo que hace la recta OP con el eje X
Despejando X e Y del sistema de dos ecuaciones con dos incógnitas, las relaciones de transformación son:
Ejemplo. Sean las coordenadas del punto P(2,6),en el sistema de referencia Oxy. Determinar las coordenadas del punto P en el sistema OXY girado un ángulo θ=60°
La ecuación de la cónica en el sistema OXY girado es
Conocida las relaciones de transformación, determinamos los valores de los coeficientes A', B', C', D', E', F'
Agrupando los términos en X2, XY, Y2, X, Y, obtenemos
Utilizamos el comando
syms X Y A B C D E th; x=X*cos(th)-Y*sin(th); y=X*sin(th)+Y*cos(th); z=expand(A*x^2+B*x*y+C*y^2+D*x+E*y); collect(z, X^2) collect(z, Y^2) collect(z, X*Y)
ans =(A*cos(th)^2 + B*cos(th)*sin(th) + C*sin(th)^2)*X^2 +... ans =(C*cos(th)^2 - B*cos(th)*sin(th) + A*sin(th)^2)*Y^2 +... ans =... + B*X*Y*cos(th)^2 - B*X*Y*sin(th)^2 - 2*A*X*Y*cos(th)*sin(th) + 2*C*X*Y*cos(th)*sin(th)
Comprobamos las siguientes invariantes
syms X Y A B C D E th; Ap=A*cos(th)^2+C*sin(th)^2+B*sin(th)*cos(th); Bp=(C-A)*sin(2*th)+B*cos(2*th); Cp=A*sin(th)^2+C*cos(th)^2-B*sin(th)*cos(th); simplify(Ap+Cp) simplify(Bp^2-4*Ap*Cp)
ans =A + C ans =B^2 - 4*A*C
Calculamos el ángulo θ que hace que el coeficientes B' del término en XY sea nulo
Clasificación de las cónicas
- Elipse, B2-4AC<0
- Parábola, B2-4AC=0
- Hipérbola, B2-4AC>0
Elipse
Sea la cónica
A=73, B=72, C=52. El discriminante B2-4AC=-10000, se trata de una elipse
Obtenemos la ecuación de la cónica en el sistema OXY girado una ángulo θ
Las relaciones de transformación son
Introduciendo x e y en la ecuación de la cónica, obtenemos la ecuación de la cónica en el sistema de referencia OXY girado
Una elipse de semiejes 1 y 2 centrada en el punto de coordenadas en X=0, e Y=1, o bien, en x=-3/5, y=4/5
syms x y X Y;
z=73*x^2+72*x*y+52*y^2+30*x-40*y-75;
th=acos(4/5);
Z=subs(z,{x,y},{X*cos(th)-Y*sin(th),X*sin(th)+Y*cos(th)});
Z=simplify(Z)
Z =100*X^2 + 25*Y^2 - 50*Y - 75
Representamos la elipse, su centro, focos y el sistema de referencia girado OXY.
syms x y;
hold on
ezplot(73*x^2+72*x*y+52*y^2+30*x-40*y-75,[-2.5,1],[-1,3])
th=acos(4/5);
line([-2*cos(th),2*cos(th)],[-2*sin(th),2*sin(th)], 'color','k') %eje X girado
line([-1*cos(th+pi/2),3.5*cos(th+pi/2)],[-1*sin(th+pi/2),3.5*sin(th+pi/2)],
'color','k')%eje Y
%centro
plot(1*cos(th+pi/2),1*sin(th+pi/2),'ro','markersize',3,'markeredgecolor',
'r','markerfacecolor','r')
%focos
c=sqrt(2^2-1);
plot((1+c)*cos(th+pi/2),(1+c)*sin(th+pi/2),'bo','markersize',3,'markeredgecolor',
'b','markerfacecolor','b')
plot((1-c)*cos(th+pi/2),(1-c)*sin(th+pi/2),'bo','markersize',3,'markeredgecolor',
'b','markerfacecolor','b')
hold off
grid on
axis equal
xlabel('x')
ylabel('y')
title('elipse girada')
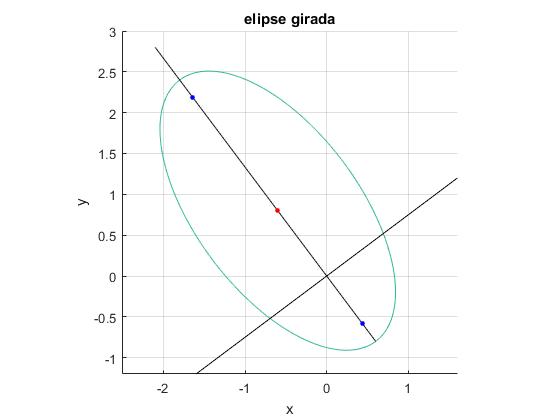
Si trasladamos el sistema de referencia al centro de la elipse x=-3/5, y=4/5, obtenemos una nueva ecuación de la cónica que carece detérminos en x e y
syms x y xp yp;
z=73*x^2+72*x*y+52*y^2+30*x-40*y-75;
zt=subs(z,{x,y},{xp-3/5,yp+4/5});
simplify(zt)
ezplot(zt,[-1.5,1.5],[-2,2])
grid on
axis equal
xlabel('x')
ylabel('y')
title('elipse girada')
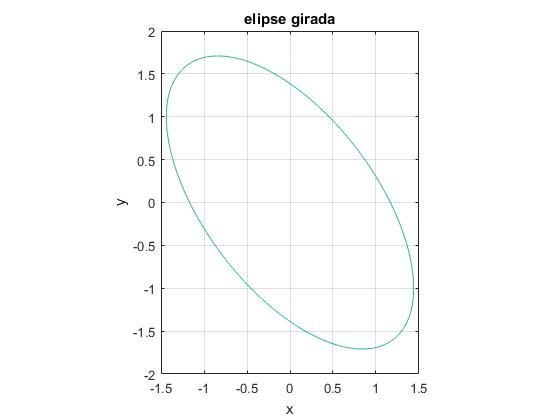
ans =73*xp^2 + 72*xp*yp + 52*yp^2 - 100
Para hallar la ecuación de la cónica en el sistema de referencia O'xy, cuyo origen se traslada a (x0, y0), sustituimos
La ecuación de la cónica es
Calculamos x0 e y0, haciendo que los coeficientes de x' y de y' sean ceros
Con A=73, B=72, C=52, D=30, E=-40, obtenemos: x0=-3/5, y0=4/5
Parábola
Sea la cónica
A=1, B=-4, C=4. El discriminante B2-4AC=0, se trata de una parábola
Como tan(2θ)=4/3. Obtenemos la ecuación de la cónica en el sistema OXY girado una ángulo θ=26.6°. cos(2θ)=3/5,
Las relaciones de transformación son
Introduciendo x e y en la ecuación de la cónica, obtenemos la ecuación de la cónica en el sistema de referencia OXY girado
syms x y X Y;
z=x^2-4*x*y+4*y^2+5*sqrt(5)*y+1;
A=1; B=-4;C=4;
disp(B^2-4*A*C)
th=atan(B/(A-C))/2;
Z=subs(z,{x,y},{X*cos(th)-Y*sin(th),X*sin(th)+Y*cos(th)});
Z=simplify(Z)
El discriminante es cero, por lo que se trata de una parábola
0 Z =5*Y^2 + 10*Y + 5*X + 1
Lo expresamos en la forma equivalente
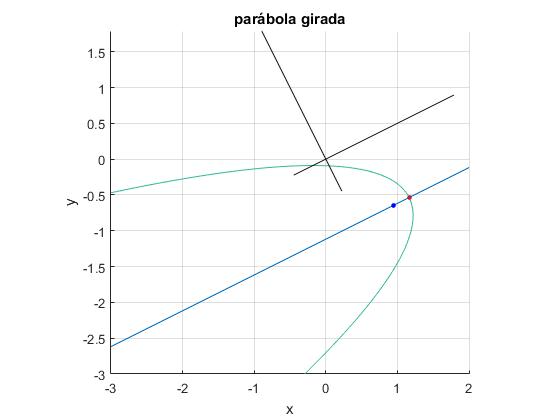
Representamos la parábola, su vértice, foco, eje y el sistema de referencia girado OXY.
syms x y;
hold on
ezplot(x^2-4*x*y+4*y^2+5*sqrt(5)*y+1,[-3,1.5],[-3,0.5])
A=1; B=-4;C=4;
th=atan(B/(A-C))/2;
line([-0.5*cos(th),2*cos(th)],[-0.5*sin(th),2*sin(th)],
'color','k') %eje X girado
line([-0.5*cos(th+pi/2),2*cos(th+pi/2)],[-0.5*sin(th+pi/2),2*sin(th+pi/2)],
'color','k')%eje Y
X0=4/5; Y0=-1; %vértice
x0=X0*cos(th)-Y0*sin(th);
y0=X0*sin(th)+Y0*cos(th);
%vértice
plot(x0,y0,'ro','markersize',3,'markeredgecolor','r',
'markerfacecolor','r')
%eje parábola
ezplot(tan(th)*(x-x0)+y0,[-3,2])
%foco
p=-1/4;
X0=4/5+p; Y0=-1;
x0=X0*cos(th)-Y0*sin(th);
y0=X0*sin(th)+Y0*cos(th);
plot(x0,y0,'bo','markersize',3,'markeredgecolor','b',
'markerfacecolor','b')
hold off
grid on
axis equal
xlabel('x')
ylabel('y')
title('parábola girada')
Hipérbola
La ecuación de la hipérbola más simple es xy-1=0
A=0, B=1, C=0. El discriminante B2-4AC>0, se trata de una hipérbola
Como tan(2θ)=∞, 2θ=π/2. Obtenemos la ecuación de la cónica en el sistema OXY girado una ángulo θ=π/4.
Las relaciones de trasnformación son
Introduciendo x e y en la ecuación de la cónica, obtenemos la ecuación de la cónica en el sistema de referencia OXY girado
syms x y X Y;
z=x*y-1;
th=pi/4;
Z=subs(z,{x,y},{X*cos(th)-Y*sin(th),X*sin(th)+Y*cos(th)});
Z=simplify(Z)
Z =X^2/2 - Y^2/2 - 1
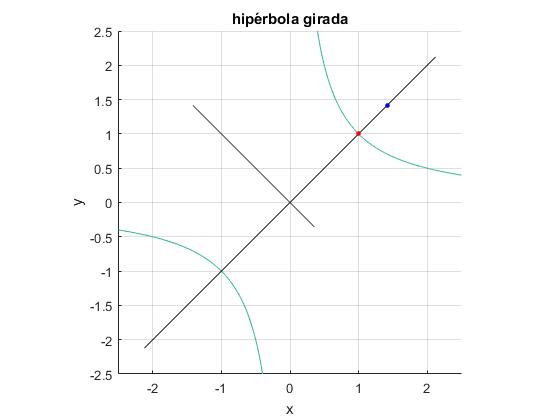
Representamos la hipérbola, su vértice, foco y el sistema de referencia girado OXY. Las asíntotas de la cónica son los ejes x e y
syms x y;
hold on
ezplot(x*y-1,[-2.5,2.5])
th=pi/4;
line([-3*cos(th),3*cos(th)],[-3*sin(th),3*sin(th)], 'color',
'k') %eje X girado
line([-0.5*cos(th+pi/2),2*cos(th+pi/2)],[-0.5*sin(th+pi/2),
2*sin(th+pi/2)], 'color','k')%eje Y
X0=sqrt(2); Y0=0; %vértice
x0=X0*cos(th)-Y0*sin(th);
y0=X0*sin(th)+Y0*cos(th);
%vértice
plot(x0,y0,'ro','markersize',3,'markeredgecolor','r','markerfacecolor','r')
%foco
c=2;
X0=c; Y0=0;
x0=X0*cos(th)-Y0*sin(th);
y0=X0*sin(th)+Y0*cos(th);
plot(x0,y0,'bo','markersize',3,'markeredgecolor','b','markerfacecolor','b')
hold off
grid on
axis equal
xlabel('x')
ylabel('y')
title('hipérbola girada')