Dos ángulos de tiro, el mismo alcance

Las ecuaciones del movimiento de los proyectiles y la ecuación de la trayectoria son

${\displaystyle \begin{array}{l}\{\begin{array}{l}{a}_x=0\\ a_y=-g\end{array}\{\begin{array}{l}{v}_x=v_0\cos \theta \\ v_y=v_0\sin \theta -gt\end{array}\{\begin{array}{l}x=v_0\cos \theta ·t\\ y=v_0\sin \theta ·t-\frac{1}{2}g{t}^2\end{array}\\ y=\tan \theta ·x-\frac{g{x}^2}{2v_0^2{\cos }^2\theta }\end{array}}$

El alcance y=0 es

${\displaystyle R=\frac{2v_0^2\sin \theta \cos \theta }{g}}$

Dado que sinα=sin(π-α), hay dos ángulos de tiro que producen el mismo alcance, el punto de impacto es el mismo, θ y π/2-θ. Por ejemplo, 30° y 60°

v0=10; %velocidad inicial
g=9.8; %aceleración de la gravedad
hold on
th=pi/6; %ángulo de tiro
fplot(@(x) x*tan(th)-g*x.^2/(2*v0^2*cos(th)^2), [0,v0^2*sin(2*th)/g])
th=pi/3; %ángulo de tiro
fplot(@(x) x*tan(th)-g*x.^2/(2*v0^2*cos(th)^2), [0,v0^2*sin(2*th)/g])
hold off
grid on
xlabel('x')
legend('30º','60º','location','best')
ylabel('y')
title('Tiro parabólico')

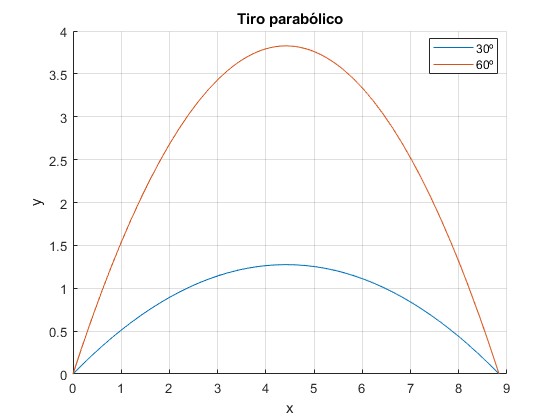
Hay dos posibles trayectorias con la misma velocidad de disparo v₀ que impactan en un punto dado, pero los ángulos de tiro ya no suman π/2, Véase la página titulada Apuntar un cañón para dar en el blanco

El vector posición y el vector velocidad son perpendiculares

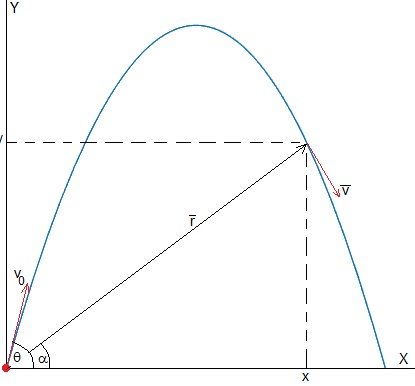
Se dispara un proyectil desde el origen con velocidad v₀ haciendo un ángulo θ con la horizontal. Vamos a demostrar que existen dos ángulos α₁ y α₂ para los cuales el vector posición y el vector velocidad son perpendiculares. Comprobaremos que la suma de estos dos ángulos α₁+α₂ es el ángulo de tiro θ

Las ecuaciones del movimiento de los proyectiles son

${\displaystyle \{\begin{array}{l}{a}_x=0\\ a_y=-g\end{array}\{\begin{array}{l}{v}_x=v_0\cos \theta \\ v_y=v_0\sin \theta -gt\end{array}\{\begin{array}{l}x=v_0\cos \theta ·t\\ y=v_0\sin \theta ·t-\frac{1}{2}g{t}^2\end{array}}$

Calculamos el tiempo t necesario para que el vector $\overrightarrow{r}$ forme un ángulo α con la horizontal

${\displaystyle \begin{array}{l}\tan \alpha =\frac{y}{x}\\ \frac{\sin \alpha }{\cos \alpha }=\frac{v_0\sin \theta ·t-\frac{1}{2}g{t}^2}{v_0\cos \theta ·t}\\ \left(v_0\sin \theta -\frac{1}{2}gt\right)\cos \alpha =v_0\cos \theta \sin \alpha \\ v_0\sin \left(\theta -\alpha \right)=\frac{1}{2}\cos \alpha ·gt\\ t=\frac{2v_0\sin \left(\theta -\alpha \right)}{g\cos \alpha }\end{array}}$

En la posición angular α, los vectores $\overrightarrow{r}$ y $\overrightarrow{v}$ son perpendiculares, el producto escalar es nulo

${\displaystyle \begin{array}{l}\overrightarrow{r}·\overrightarrow{v}=0\\ \left(v_0\cos \theta ·t·\widehat{i}+\left(v_0\sin \theta ·t-\frac{1}{2}g{t}^2\right)\widehat{j}\right)\left(v_0\cos \theta ·\widehat{i}+\left(v_0\sin \theta -gt\right)\widehat{j}\right)=0\\ v_0^2{\cos }^2\theta +\left(v_0\sin \theta -\frac{1}{2}gt\right)\left(v_0\sin \theta -gt\right)=0\\ \frac{1}{2}{g}^2{t}^2-\frac{3}{2}g{v}_0\sin \theta ·t+v_0^2=0\end{array}}$

Sustituimos el tiempo t, obteniendo una ecuación de segundo grado en tanα

${\displaystyle \begin{array}{l}\frac{1}{2}{g}^2{\left(\frac{2v_0\sin \left(\theta -\alpha \right)}{g\cos \alpha }\right)}^2-\frac{3}{2}g{v}_0\sin \theta \left(\frac{2v_0\sin \left(\theta -\alpha \right)}{g\cos \alpha }\right)+v_0^2=0\\ -\frac{\sin \left(\theta -\alpha \right)}{{\cos }^2\alpha }\left(\sin \theta \cos \alpha +2\sin \alpha \cos \theta \right)+1=0\\ {\cos }^2\theta {\cos }^2\alpha -\sin \theta \cos \alpha \sin \alpha \cos \theta +2{\sin }^2\alpha {\cos }^2\theta =0\\ 2\cos \theta ·{\tan }^2\alpha -\sin \theta ·\tan \alpha +\cos \theta =0\end{array}}$

Las raíces de la ecuación de segundo grado son

${\displaystyle \begin{array}{l}\tan {\alpha }_1=\frac{\sin \theta +\sqrt{{\sin }^2\theta -8{\cos }^2\theta }}{4\cos \theta }\\ \tan {\alpha }_2=\frac{\sin \theta -\sqrt{{\sin }^2\theta -8{\cos }^2\theta }}{4\cos \theta }\end{array}}$

Para que existan raíces reales, sin²θ>8·cos²θ, es decir θ>70.5°

Aplicando la fórmula de la tangente de la suma de dos ángulos

${\displaystyle \begin{array}{l}\tan \left({\alpha }_1+{\alpha }_2\right)=\frac{\sin \left({\alpha }_1+{\alpha }_2\right)}{\cos \left({\alpha }_1+{\alpha }_2\right)}=\frac{\sin {\alpha }_1\cos {\alpha }_2+\cos {\alpha }_1\sin {\alpha }_2}{\cos {\alpha }_1\cos {\alpha }_2-\sin {\alpha }_1\sin {\alpha }_2}=\frac{\tan {\alpha }_1+\tan {\alpha }_2}{1-\tan {\alpha }_1·\tan {\alpha }_2}\\ \tan \left({\alpha }_1+{\alpha }_2\right)=\frac{\frac{2\sin \theta }{4\cos \theta }}{1-\frac{8{\cos }^2\theta }{16{\cos }^2\theta }}=\tan \theta \\ \theta ={\alpha }_1+{\alpha }_2\end{array}}$

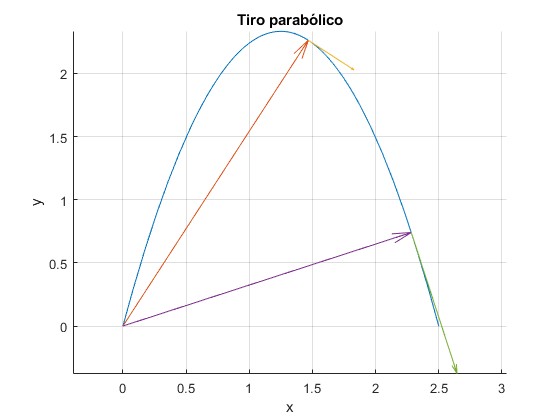
Representamos la trayectoria de un proyectil dispado con velocidad v₀=10 m/s haciendo un ángulo θ=75° (θ>70.5°) con la horizontal. Representamos el vector posición y el vector velocidad para las dos posiciones ángulares α=57° y 18° que suman el ángulo de tiro 75°

hold on
v0=7; %velocidad de disparo
th=75*pi/180; %ángulo de tiro
tVuelo=2*v0*sin(th)/9.8; %tiempo de vuelo
x=@(t) v0*cos(th)*t;
y=@(t) v0*sin(th)*t-4.9*t.^2;
vy=@(t) v0*sin(th)-9.8*t;
fplot(x, y ,[0,tVuelo])
alfa_1=atan((sin(th)+sqrt(sin(th)^2-8*cos(th)^2))/(4*cos(th)));
alfa_2=atan((sin(th)-sqrt(sin(th)^2-8*cos(th)^2))/(4*cos(th)));
t1=2*v0*sin(th-alfa_1)/(9.8*cos(alfa_1));
t2=2*v0*sin(th-alfa_2)/(9.8*cos(alfa_2));
quiver(0,0,x(t1),y(t1),1)
quiver(x(t1),y(t1),v0*cos(th),vy(t1),0.2)
quiver(0,0,x(t2),y(t2),1)
quiver(x(t2),y(t2),v0*cos(th),vy(t2),0.2)
hold off
grid on
axis equal
xlabel('x')
ylabel('y')
title('Tiro parabólico')

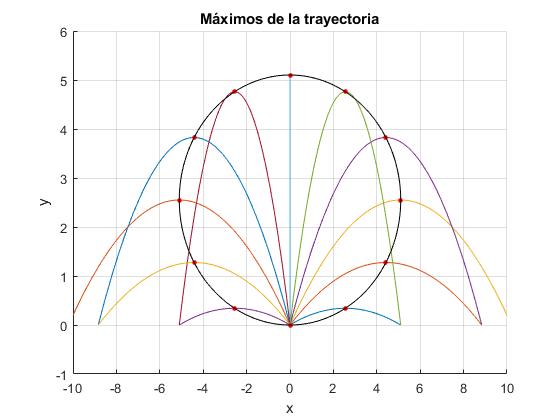
La elipse que une las posiciones de altura máxima

La altura máxima se alcanza cuando v_y=0, en el intante t=v₀·sinθ/g. La posición (x_m, y_m) del proyectil en este instante es

${\displaystyle x_m=\frac{v_0^2}{2g}\text{sin}(2\theta )y_m=\frac{v_0^2}{2g}{\text{sin}}^2\theta }$

Teniendo en cuenta, la relación trigonométrica 1-cos(2θ)=2sin²θ

${\displaystyle x_m=\frac{v_0^2}{2g}\text{sin}(2\theta )y_m=\frac{v_0^2}{4g}\left(1-\cos (2\theta )\right)}$

Despejando sin(2θ) en la primera ecuación, cos(2θ), en la segunda, elevando al cuadrado y sumando, eliminamos el ángulo 2θ.

${\displaystyle \frac{x_m^2}{4b^2}+\frac{{(y_m-b)}^2}{b^2}=1b=\frac{v_0^2}{4g}}$

Esta ecuación representa una elipse centrada en el punto (0, b) cuyos semiejes son 2b y b

v0=10; %velocidad inicial
g=9.8; %aceleración de la gravedad
hold on
for ang=(15:15:180)*pi/180
    %trayectorias
    T=2*v0*sin(ang)/g;
    fplot(@(t) v0*cos(ang)*t, @(t) v0*sin(ang)*t-g*t.^2/2,[0,T]);
    %máximos
    xm=v0^2*sin(2*ang)/(2*g); 
    ym=v0^2*sin(ang)^2/(2*g);
    plot(xm,ym,'ro','markersize',3,'markeredgecolor','r','markerfacecolor','r')
end
%elipse
b=v0^2/(4*g);
x=linspace(-2*b,2*b, 50);
y=b*(1+sqrt(1-x.^2/(4*b^2))); %media elipse
plot([x,fliplr(x)],[y,2*b-y],'k')
hold off
grid on
xlim([-10,10])
xlabel('x')
ylabel('y')
title('Máximos de la trayectoria')

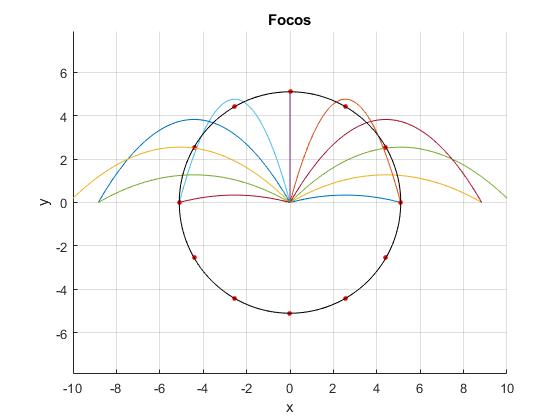
La circunferencia que une los focos de las parábolas

Sea la parábola de ecuación, $y=-\frac{1}{4p}{x}^2$. El vértice está en el origen (0,0) y el foco, una distancia p por debajo, tal como se aprecia en la figura de la izquierda

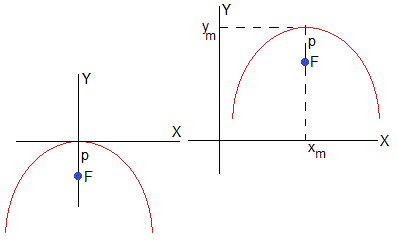
Sea una parábola de ecuación y=ax²+bx+c, con a<0. Conocidas las coordenadas del vértice (máximo), las coordenadas del foco son

${\displaystyle x_F=x_m,y_F=y_m+\frac{1}{4a},a<0}$

En la ecuación de la trayectoria el coeficiente a es

${\displaystyle \begin{array}{l}y=x\tan \theta -\frac{g{x}^2}{2v_0^2{\cos }^2\theta },\\ a=-\frac{g}{2v_0^2{\cos }^2\theta }\end{array}}$

Las coordenadas del foco son

${\displaystyle \begin{array}{l}{x}_F=\frac{v_0^2}{2g}\sin \left(2\theta \right)\\ y_F=\frac{v_0^2{\sin }^2\theta }{2g}-\frac{v_0^2{\cos }^2\theta }{2g}=-\frac{v_0^2}{2g}\cos \left(2\theta \right)\end{array}}$

Cumplen que

${\displaystyle x_F^2+y_F^2={\left(\frac{v_0^2}{2g}\right)}^2}$

Que es la ecuación de una circunferencia centrada en el origen de radio $r=\frac{v_0^2}{2g}$

v0=10; %velocidad inicial
g=9.8; %aceleración de la gravedad
hold on
for ang=(15:15:180)*pi/180
    %trayectorias
    T=2*v0*sin(ang)/g;
    fplot(@(t) v0*cos(ang)*t, @(t) v0*sin(ang)*t-g*t.^2/2,[0,T]);
    %focos
    xF=v0^2*sin(2*ang)/(2*g); 
    yF=-v0^2*cos(2*ang)/(2*g);
    plot(xF,yF,'ro','markersize',3,'markeredgecolor','r','markerfacecolor','r')
end
%circunferencia
r=v0^2/(2*g);
fplot(@(t) r*cos(t), @(t) r*sin(t),[0,2*pi], 'color','k')
hold off
axis equal
grid on
xlim([-10,10])
xlabel('x')
ylabel('y')
title('Focos')

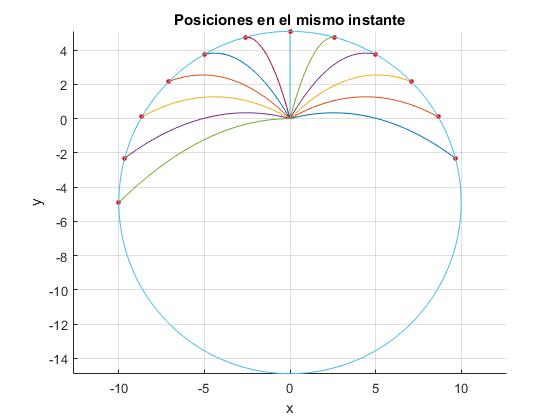
La circunferencia que une las posiciones en el instante t

Se disparan en el mismo instante poyectiles con la misma velocidad v₀ con varios ángulos ángulos de tiro θ. Escribimos la posición de los proyectiles en el instante t

${\displaystyle \begin{array}{l}x=v_0\cos \theta ·t\hfill \\ y+\frac{1}{2}g{t}^2=v_0\sin \theta ·t\hfill \end{array}}$

Elevando al cuadrado y sumando, obtenemos la ecuación de una circunferencia de radio v₀t centrada en el punto x=0, y=-gt²/2

${\displaystyle x^2+\left(y+\frac{1}{2}g{t}^2\right)={\left(v_{0}t\right)}^2}$

v0=10; %velocidad inicial
g=9.8; %aceleración de la gravedad

hold on
T=1; %instante
for ang=(15:15:180)*pi/180
    %trayectorias
    x=@(t) v0*cos(ang)*t;
    y=@(t) v0*sin(ang)*t-g*t.^2/2;
    fplot(x ,y ,[0,T]);
    %posición en el instante T
    plot(x(T),y(T),'ro','markersize',3,'markeredgecolor','r','markerfacecolor','r')
end
%circunferencia
fplot(@(ang) v0*T*cos(ang), @(ang) v0*T*sin(ang)-g*T^2/2, [0,2*pi])
hold off
grid on
axis equal
xlabel('x')
ylabel('y')
title('Posiciones en el mismo instante')

Referencias

Fernández-Chapou J. L., Salas-Brito A. L., Vargas C. A. An elliptic property of parabolic trajectories. Am. J. Phys. 72 (8) August 2004, pp. 1109

Indian National Physics Olympiad. Homi Bhabha Centre for Science Eduaction. Solved papers NSEP & INPhO, 2016-2018, Example 24, pp. 20-21