Disparando a un objeto que cae

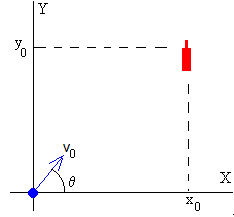
Una objeto se deja caer desde el reposo en el instante en que un proyectil es lanzadado desde el origen.

Determinaremos los valores del ángulo y de la velocidad de disparo para que el proyectil impacte en el objeto.

El movimiento del proyectil se realiza bajo la aceleración constante de la gravedad, es decir, es la composición de dos movimientos

Uniforme a lo largo del eje horizontal
Uniformemente acelerado a lo largo del eje vertical.

$\vec{a} {\begin{cases} a_{x} = 0 \\ a_{y} = - g \end{cases} \vec{v} {\begin{cases} v_{x} = v_{0} \cos θ \\ v_{y} = v_{0} \sin θ - g t \end{cases} \vec{r} {\begin{cases} x = v_{0} \cos θ \cdot t \\ y = v_{0} \sin θ \cdot t - \frac{1}{2} g t^{2} \end{cases}$

La ecuación de la trayectoria es

$y = x \tan θ + \frac{1}{2} g \frac{x^{2}}{v_{0}^{2} \cos^{2} θ} = x \tan θ + \frac{1}{2} g (1 + \tan^{2} θ) \frac{x^{2}}{v_{0}^{2}}$

El objeto se mueve verticalmente bajo la aceleración constante de la gravedad

a=-g
v=-g·t
y=y₀-gt²/2

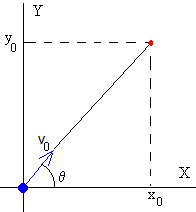
Cuando se produce el choque, la posición del proyectil y del objeto coinciden

$\begin{array}{l} x_{0} = v_{0} \cos θ t \\ y_{0} - \frac{1}{2} g t^{2} = v_{0} \sin θ t - \frac{1}{2} g t^{2} \end{array}$

Dividimos la segunda ecuación entre la primera.

$\tan θ = \frac{y_{0}}{x_{0}}$

Para impactar sobre el objeto debemos de apuntarlo directamente y en el instante en el que se deja caer, se dispara.

El impacto se produce en el suelo y=0

Calculamos la velocidad con la que disparamos el proyectil v₀ para que el impacto con el objeto tenga lugar en el suelo y=0

El tiempo que tarda en caer el objeto desde una altura y₀ es

$t = \sqrt{\frac{2 y_{0}}{g}}$

El alcance x₀ del proyectil es

$x_{0} = v_{0} \cos θ \sqrt{\frac{2 y_{0}}{g}}$

Conocido tanθ=y₀/x₀, calculamos cosθ, empleando la relación

$\cos^{2} θ = \frac{1}{1 + \tan^{2} θ}$

Despejamos la velocidad inicial v₀

$v_{0} = \sqrt{\frac{g (x_{0}^{2} + y_{0}^{2})}{2 y_{0}}}$

Ejemplo:

La posición del objeto x₀=50 m e y₀=30 m

El ángulo de tiro es tanθ=30/50, θ=31º

Supongamos que la velocidad de disparo v₀=20 m/s. El impacto tiene lugar en la posición x=50 m y en el instante

20·cos31º·t=50, donde t=2.92 s

En este instante el objeto se encuentra en

y=y₀-gt²/2, es decir, y=30-9.8·2.92²/2=-11.65 m

Si la velocidad de disparo fuese de v₀=40 m/s, el impacto se produciría cuando el objeto se encontrase en y=19.2 m sobre el suelo.

Para que el impacto se produzca en el suelo y=0, la velocidad de disparo calculada mediante la fórmula, será v₀=23.6 m/s

El impacto se produce cuando el proyectil alcanza su altura máxima, v_y=0

Calculamos la velocidad con la que disparamos el proyectil v₀ para que el impacto con el objeto se produzca cuando el proyectil alcanza su altura máxima.

En el vértice de la parábola, la componente Y velocidad del proyectil es cero, v_y=0, el tiempo t que tarda el proyectil en alcanzar esta posición es, t=v₀sinθ/g

La posición del proyectil en este instante es

$\begin{array}{l} y = \frac{1}{2} \frac{v_{0}^{2} \sin^{2} θ}{g} \\ x = \frac{v_{0}^{2}}{g} \sin θ \cos θ \end{array}$

La posición del objeto en dicho instante es

$\begin{array}{l} x = x_{0} \\ y = y_{0} - \frac{1}{2} \frac{v_{0}^{2}}{g} \sin^{2} θ \end{array}$

Conocido tanθ=y₀/x₀, para que coincidan las posciones de ambos cuerpos

$\begin{array}{l} x_{0} = \frac{v_{0}^{2}}{g} \frac{\tan θ}{1 + \tan^{2} θ} \\ v_{0} = \sqrt{\frac{g (x_{0}^{2} + y_{0}^{2})}{y_{0}}} \end{array}$

Ejemplo:

La posición del objeto x₀=50 m e y₀=30 m

Ya hemos calculado el ángulo de tiro, tanθ=30/50, θ=31º

La velocidad de disparo v₀=33.3 m/s para el impacto tenga lugar en el vértice de la parábola

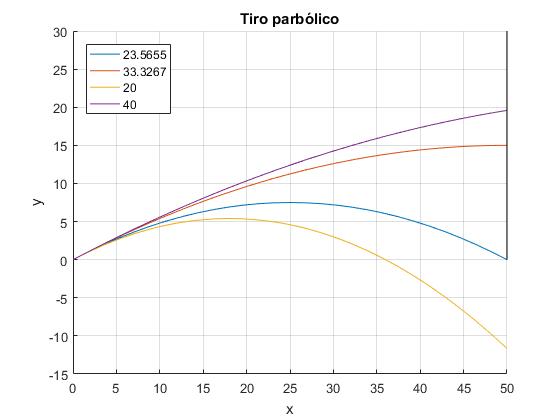
Elaboramos un script para respresentar las trayectorias del proyectil hasta el punto de impacto para varias velocidades v₀ de disparo: para que el impacto tenga lugar en el suelo, en el vértice de la parábola, cuando v₀=20 m/s o cuando v₀=40 m/s

x0=50; %posición inicial del objeto
y0=30; 
th=atan(y0/x0); %ángulo de tiro

hold on
%velocidad de disparo
for v0=[sqrt(9.8*(x0^2+y0^2)/(2*y0)), sqrt(9.8*(x0^2+y0^2)/y0), 20, 40] 
    fplot(@(x) x*tan(th)-4.9*x.^2*(1+tan(th)^2)/v0^2, [0,x0], 
'displayName',num2str(v0))
end
hold off
legend('-DynamicLegend','location','northwest')
line([x0,x0],[y0,0], 'color','k')
grid on
xlabel('x')
ylabel('y')
title('Tiro parbólico')

Actividades

Al pulsar el botón titulado Nuevo, el programa genera dos números aleatorios que representan la posición (x₀, y₀) del objeto.

Se introduce

El ángulo de tiro, en el control titulado Angulo de tiro
La velocidad de disparo, en el control titulado Velocidad disparo.

Se pulsa el botón ►.

Si no se acierta, se vuelve a introducir un nuevo ángulo de tiro y a continuación, se pulsa el botón titulado ►.

Angulo
Velocidad disparo

Los instantes en los que se libera el objeto y se dispara el proyectil no coinciden

Supongamos que el proyectil se dispara en el instante t=0, y el objeto se deja caer en el instante t=t₀ (que puede ser positivo o negativo).

La posición del proyectil es

${\begin{cases} x = v_{0} \cos θ \cdot t \\ y = v_{0} \sin θ \cdot t - \frac{1}{2} g t^{2} \end{cases}$

La posición del objeto es

${\begin{cases} x = x_{0} \\ y = y_{0} - \frac{1}{2} g {(t - t_{0})}^{2} \end{cases}$

Para que coincidan ambas posiciones

${\begin{cases} x_{0} = v_{0} \cos θ \cdot t \\ v_{0} \sin θ \cdot t - \frac{1}{2} g t^{2} = y_{0} - \frac{1}{2} g {(t - t_{0})}^{2} \end{cases}$

Eliminado el tiempo t, obtenemos la ecuación

$\begin{array}{l} \tan θ - A = \frac{B}{\cos θ} \\ A = \frac{1}{x_{0}} (y_{0} - \frac{1}{2} g t_{0}^{2}) B = \frac{g t_{0}}{v_{0}} \end{array}$

Elevando al cuadrado y teniendo en cuenta que $\frac{1}{\cos^{2} θ} = a + \tan^{2} θ$

Obtenemos la ecuación de segundo grado en tanθ

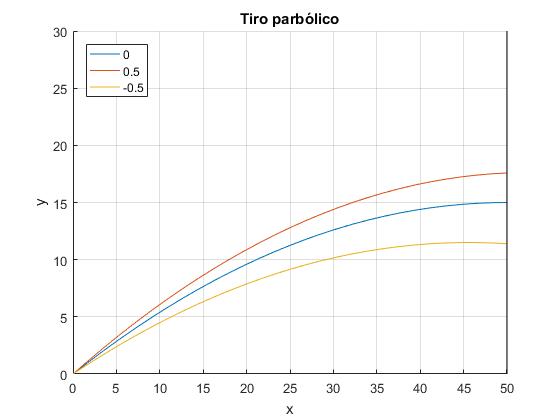
$\begin{array}{l} (1 - B^{2}) \tan^{2} θ - 2 A \tan θ + A^{2} - B^{2} = 0 \\ \tan θ = \frac{A + B \sqrt{1 + A^{2} - B^{2}}}{1 - B^{2}} \end{array}$

Elaboramos un script para representar las trayectorias de un proyectil que impacta con un objeto inicialmente situado en el punto x₀=50 m, y₀=30 m. La velocidad inicial de disparo v₀ es la que produce un impacto en el vértice de la parábola cuando se libera el objeto a la vez que se dispara el proyectil, t₀=0 s. Las otras dos trayectorias se producen cuando el disparo se retrasa o se adelanta, t₀=±0.5 s.

x0=50; %posición inicial del objeto
y0=30; 
v0=sqrt(9.8*(x0^2+y0^2)/y0); %velocidad de disparo

hold on
for t0=[0,0.5,-0.5]
    A=(y0-4.9*t0^2)/x0;
    B=9.8*t0/v0;
    th=atan((A+B*sqrt(1*A^2-B^2))/(1-B^2));
    fplot(@(x) x*tan(th)-4.9*x.^2*(1+tan(th)^2)/v0^2, [0,x0],
 'displayName',num2str(t0))
end
hold off
legend('-DynamicLegend','location','northwest')
line([x0,x0],[y0,0], 'color','k')
grid on
xlabel('x')
ylabel('y')
title('Tiro parbólico')

Referencias