Una rana salta un tronco.

Un tronco cilíndrico de radio R, yace en el suelo. Una rana intenta saltarlo siguiendo una trayectoria parabólica tal como se muestra en la figura. Vamos a calcular la velocidad v₀ mínima de disparo, el ángulo de tiro θ y la distancia x₀ al troco.

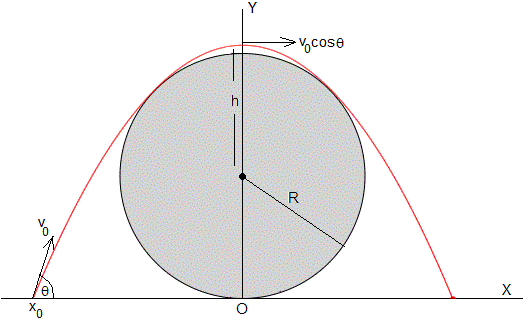
Vamos a estudiar una trayectoria parabólica simétrica respecto del eje Y, es decir, la posición de disparo es -x₀ y la de impacto x₀, el alcance sería 2x₀ y la altura máxima R+h

$\vec{a} {\begin{cases} a_{x} = 0 \\ a_{y} = - g \end{cases} \vec{v} {\begin{cases} v_{x} = - x v_{0} \cos θ \\ v_{y} = v_{0} \sin θ - g t \end{cases} \vec{r} {\begin{cases} x = - x_{0} + v_{0} \cos θ \cdot t \\ y = v_{0} \sin θ t - \frac{1}{2} g t^{2} \end{cases}$

La altura máxima se alcanza cuando v_y=0

$\begin{array}{l} t = \frac{v_{0} \sin θ}{g} \\ R + h = v_{0} \sin θ \frac{v_{0} \sin θ}{g} - \frac{1}{2} g {(\frac{v_{0} \sin θ}{g})}^{2} = \frac{1}{2} \frac{v_{0}^{2} \sin^{2} θ}{g} \end{array}$

En el tiempo t que tarda el proyectil en alcanzar la altura máxima, se desplaza desde -x₀ hasta el origen x=0 o desde el origen hasta la posición de impacto x₀

$0 = - x_{0} + v_{0} \cos θ \frac{v_{0} \sin θ}{g} x_{0} = \frac{1}{2} \frac{v_{0}^{2} \sin (2 θ)}{g}$

Tiempo de vuelo es el doble que el empleado en alcanzar la máxima altura

$T = 2 \frac{v_{0} \sin θ}{g}$

Trayectoria tangente a la circunferencia de radio R

Dado que la trayectoria es simétrica, situamos el origen en el centro del tronco y tomamos la velocidad de disparo v₀cosθ a una altura h por encima del centro. Las ecuaciones del movimiento del proyectil respecto del nuevo origen, son simples:

x=v₀cosθ·t
y=h-gt²/2

La trayectoria parabólica es tangente a la circunferencia de radio R, por lo que x²+y²=R²

$\begin{array}{l} {(v_{0} \cos θ \cdot t)}^{2} + {(h - \frac{1}{2} g t^{2})}^{2} = R^{2} \\ \frac{g^{2}}{4} t^{4} + ({(v_{0} \cos θ)}^{2} - g h) t^{2} + (h^{2} - R^{2}) = 0 \\ t^{2} = \frac{- ({(v_{0} \cos θ)}^{2} - g h) \pm \sqrt{{({(v_{0} \cos θ)}^{2} - g h)}^{2} - g^{2} (h^{2} - R^{2})}}{g^{2} / 2} \end{array}$

Por simetría los tiempos tiene que ser iguales y de signo contrario, por lo que el discriminante deberá ser nulo

$\begin{array}{l} {({(v_{0} \cos θ)}^{2} - g h)}^{2} - g^{2} (h^{2} - R^{2}) = 0 \\ {(v_{0} \cos θ)}^{2} = g (h \pm \sqrt{h^{2} - R^{2}}) \end{array}$

La solución con signo positivo no es posible ya que daría un tiempo t²<0

$v_{0} \cos θ = \sqrt{g (h - \sqrt{h^{2} - R^{2}})}$

Conocida la velocidad en el punto más alto de la trayectoria v₀cosθ, aplicamos el principio de conservación de la energía para calcular la velocidad de disparo v₀

$\begin{array}{l} \frac{1}{2} m v_{0}^{2} = m g (h + R) + \frac{1}{2} m {(v_{0} \cos θ)}^{2} \\ v_{0}^{2} = g (3 h + 2 R - \sqrt{h^{2} - R^{2}}) \end{array}$

hold on
ang=(1:360)*pi/180; %tronco
fill(cos(ang),1+sin(ang),'y')
R=1; %radio del tronco
h=1.5; %altura desde el centro del tronco
v0=sqrt(9.8*(3*h+2*R-sqrt(h^2-R^2))); %velocidad de disparo
th=acos(sqrt(9.8*(h-sqrt(h^2-R^2)))/v0); %ángulo de tiro
x0=v0^2*sin(2*th)/(2*9.8); %posición de disparo
tVuelo=2*x0/(v0*cos(th)); %tiempo de vuelo
fplot(@(t) -x0+v0*cos(th)*t, @(t) v0*sin(th)*t-4.9*t.^2,[0,tVuelo])
hold off
grid on
axis equal
xlabel('x')
ylabel('y')
title('Tiro parabólico')

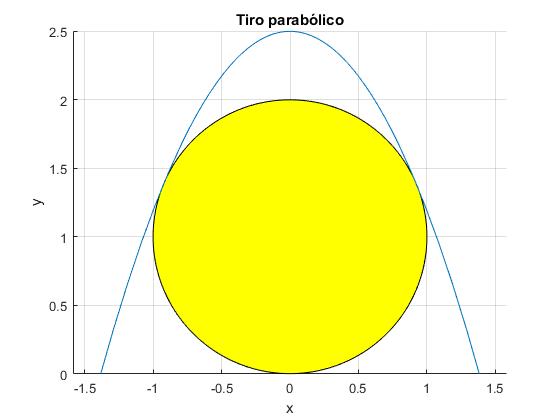
En el script se calculan: la velocidad de disparo v₀=7.26 m/s, el ángulo de tiro θ=74.5°, la posición de disparo x₀=-1.38 m y el tiempo de vuelo T=1.43 s

>> v0
v0 =    7.2625
>> th*180/pi
ans =   74.5496
>> x0
x0 =    1.3820
>> tVuelo
tVuelo =    1.4286

Velocidad mínima

Velocidad de disparo

Calculamos el mínimo de v₀, derivando con respecto de h

$\begin{array}{l} \frac{d v_{0}^{2}}{d h} = g (3 - \frac{h}{\sqrt{h^{2} - R^{2}}}) = 0 \\ h_{m} = \frac{3 \sqrt{2}}{4} R \\ v_{m} = \sqrt{2 (1 + \sqrt{2}) g R} \end{array}$

Angulo de tiro

La altura máxima es R+h_m, que se alcanza cuando la velocidad vertical v_y es nula

$\begin{array}{l} {\begin{cases} v_{m} \sin θ_{m} - g t = 0 \\ R + h_{m} = v_{m} \sin θ_{m} t - \frac{1}{2} g t^{2} \end{cases} \\ \sin^{2} θ_{m} = \frac{2 g (R + h_{m})}{v_{m}^{2}} = \frac{1}{4} (\sqrt{2} + 2) \end{array}$

El ángulo de disparo θ_m=67.5°, para la velocidad de disparo mínima

Posición de disparo

En el tiempo t que tarda el proyectil en alcanzar la altura máxima, se desplaza desde -x₀ hasta el origen x=0

$x_{0} = v_{m} \cos θ_{m} \frac{v_{m} \sin θ_{m}}{g} = \frac{1}{2} (\sqrt{2} + 2) R$

Tiempo de vuelo

Es el doble que el empleado en alcanzar la máxima altura

$T = 2 \frac{v_{m} \sin θ_{m}}{g} = \sqrt{2 (4 + 3 \sqrt{2})} \sqrt{\frac{R}{g}}$

hold on
ang=(1:360)*pi/180; %tronco
fill(cos(ang),1+sin(ang),'y')
R=1; %radio del tronco
v0=sqrt(2*(1+sqrt(2))*9.8*R); %velocidad de disparo
th=asin(sqrt(sqrt(2)+2)/2); %ángulo de tiro
x0=(sqrt(2)+2)*R/2; %posición de disparo
tVuelo=sqrt(2*(4+3*sqrt(2)))*sqrt(R/9.8); %tiempo de vuelo
fplot(@(t) -x0+v0*cos(th)*t, @(t) v0*sin(th)*t-4.9*t.^2,[0,tVuelo])
hold off
grid on
axis equal
xlabel('x')
ylabel('y')
title('Tiro parabólico')

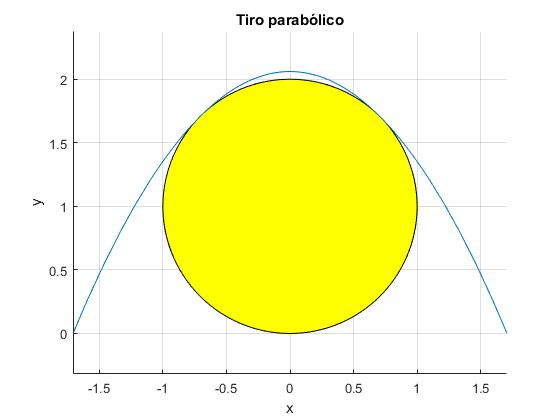
En el script se calculan: la velocidad de disparo v₀=6.88 m/s, el ángulo de tiro θ=67.5°, la posición de disparo x₀=-1.71 m, el tiempo de vuelo T=1.30 s y la altura máxima medida desde el centro del tronco, h_m=1.06 m, 6 cm por encima del tronco.

>> v0
v0 =    6.8789
>> th*180/pi
ans =   67.5000
>> x0
x0 =    1.7071
>> tVuelo
tVuelo =    1.2970
>> hm=3*sqrt(2)*R/4
hm =    1.0607

Actividades

Se introduce

La velocidad de disparo v₀, en el control titulado Velocidad
El ángulo de tiro, θ, en el control titulado Angulo
La posición de disparo -x₀ a la izquierda del origen en el control titulado Distancia

Se pulsa el botón titulado Nuevo

Se traza la trayectoria parabólica seguida por la rana de acuerdo con las ecuaciones

Cuando el proyectil choca con el tronco, es decir, cuando su distancia al centro del tronco es menor que R el movimiento se detiene

$x^{2} + {(y - R)}^{2} \leq R^{2}$

El movimiento también se detiene cuando el proyectil llega al suelo, y=0

Velocidad : Angulo:
Distancia:

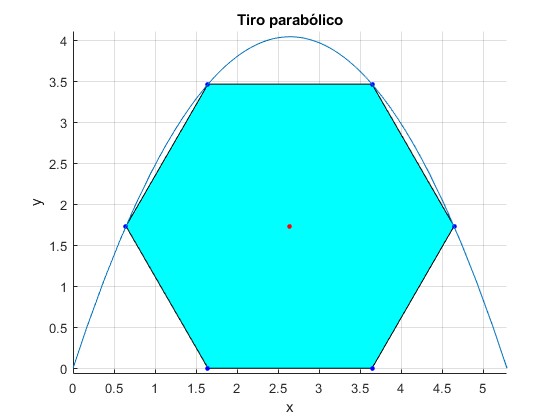
Tronco hexagonal

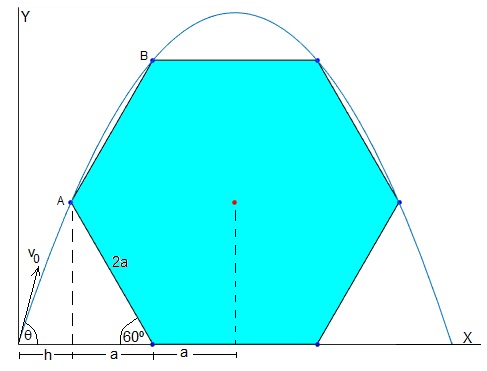
Se dispara un proyectil desde el origen, con velocidad v₀, haciendo un ángulo θ con la horizontal. La trayectoria del proyectil pasa por cuatro vértices del hexágono de lado 2a, tal como se muestra en la figura.

La ecuación de la trayectoria es

$\begin{array}{l} {\begin{cases} a_{x} = 0 \\ a_{y} = - g \end{cases} {\begin{cases} v_{x} = v_{0} \cos θ \\ v_{y} = v_{0} \sin θ - g t \end{cases} {\begin{cases} x = v_{0} \cos θ \cdot t \\ y = v_{0} \sin θ \cdot t - \frac{1}{2} g t^{2} \end{cases} \\ y = \tan θ \cdot x - \frac{g x^{2}}{2 v_{0}^{2} \cos^{2} θ} \end{array}$

El alcance y=0 es

$R = \frac{2 v_{0}^{2} \sin θ \cos θ}{g}$

Ecuaciones

La trayectoria pasa por el punto A (h, 2asin60°)

$a \sqrt{3} = \tan θ \cdot h - \frac{g h^{2}}{2 v_{0}^{2} \cos^{2} θ}$

La trayectoria pasa por el punto B (h+a, 4asin60°)

$2 a \sqrt{3} = \tan θ \cdot (h + a) - \frac{g {(h + a)}^{2}}{2 v_{0}^{2} \cos^{2} θ}$

El alcance del proyectil es 2(h+2a)

$\begin{array}{l} 2 h + 4 a = \frac{2 v_{0}^{2} \sin θ \cos θ}{g} \\ v_{0}^{2} = \frac{(h + 2 a) g}{\sin θ \cos θ} \end{array}$

Las tres incógnitas son:

posición inicial, h respecto del vértice A del hexágono
la velocidad inicial, v₀
el ángulo que hace con la horizontal, θ

Combinamos la primera y segunda ecuación

$\begin{array}{l} 2 a \sqrt{3} = a \tan θ + h \tan θ - \frac{g h^{2}}{2 v_{0}^{2} \cos^{2} θ} - \frac{g a (2 h + a)}{2 v_{0}^{2} \cos^{2} θ} \\ \sqrt{3} = \tan θ - \frac{g (2 h + a)}{2 v_{0}^{2} \cos^{2} θ} \end{array}$

Introducimos el cuadrado de la velocidad inicial en la ecuación anterior

$\begin{array}{l} \sqrt{3} = \tan θ - \frac{g (2 h + a)}{2 \cos^{2} θ} \frac{\sin θ \cos θ}{(h + 2 a) g} \\ \sqrt{3} = \tan θ - \frac{2 h + a}{2 (h + 2 a)} \tan θ \\ \tan θ = \frac{2 (h + 2 a)}{\sqrt{3} a} \end{array}$

Posición inicial, h

Introducimos en la primera ecuación, el cuadrado de la velocidad inicial y tanθ

$\begin{array}{l} a \sqrt{3} = \tan θ \cdot h - \frac{g h^{2}}{2 v_{0}^{2} \cos^{2} θ} \\ a \sqrt{3} = \tan θ \cdot h - \frac{g h^{2}}{2 \cos^{2} θ} \frac{\sin θ \cos θ}{(h + 2 a) g} \\ a \sqrt{3} = (\frac{h (h + 4 a)}{2 (h + 2 a)}) \tan θ \\ a \sqrt{3} = (\frac{h (h + 4 a)}{2 (h + 2 a)}) \frac{2 (h + 2 a)}{\sqrt{3} a} \\ h^{2} + 4 a h - 3 a^{2} = 0 \end{array}$

La solución positiva de la ecuación de segundo grado es

$h = (\sqrt{7} - 2) a$

El ángulo que hace con la horizontal, θ

$\tan θ = \frac{2 (h + 2 a)}{\sqrt{3} a} = 2 \sqrt{\frac{7}{3}}$

La velocidad inicial, v₀

Utilizamos las relaciones trigonométricas

$\sin θ = \frac{\tan θ}{\sqrt{1 + \tan^{2} θ}}, \cos θ = \frac{1}{\sqrt{1 + \tan^{2} θ}}$

El resultado es

$\begin{array}{l} v_{0}^{2} = \frac{(h + 2 a) g}{\sin θ \cos θ} \\ \sin θ \cos θ = \frac{\tan θ}{1 + \tan^{2} θ} = \frac{2 \sqrt{\frac{7}{3}}}{1 + \frac{28}{3}} \\ v_{0}^{2} = \frac{31}{2 \sqrt{3}} a g \end{array}$

Alcance

$R = 2 (h + 2 a) = 2 \sqrt{7} a$

También se puede calcular a partir de la fórmula del alcance en el tiro parabólico

Tiempo de vuelo

Poniendo y=0 en la ecuación de la trayectoria

$\begin{array}{l} 0 = v_{0} \sin θ \cdot t - \frac{1}{2} g t^{2} \\ T = \frac{2 v_{0} \sin θ}{g} \\ T^{2} = \frac{4 v_{0}^{2} \sin^{2} θ}{g^{2}} = 4 \frac{31}{2 \sqrt{3}} \frac{a g}{g^{2}} \frac{4 \frac{7}{3}}{1 + \frac{28}{3}} = \frac{56}{\sqrt{3}} \frac{a}{g} \end{array}$

Es el cuadrado del tiempo de vuelo

a=1; %lado del hexágono 2a
h=-2+sqrt(7)*a;
xc=h+2*a; %centro,
yc=a*sqrt(3);
hold on
x1=xc+2*a*cos((1:6)*pi/3);
y1=yc+2*a*sin((1:6)*pi/3);
fill(x1,y1,'c')
plot(x1,y1,'bo','markersize',3,'markerfacecolor','b')  
plot(xc,yc,'ro','markersize',3,'markerfacecolor','r') 
v0=sqrt(31*a*9.8/(2*sqrt(3))); %velocidad de disparo
th=atan(2*sqrt(7/3)); %ángulo de tiro
T=sqrt(56*a/(sqrt(3)*9.8)); %tiempo de vuelo
x=@(t) v0*cos(th)*t;
y=@(t) v0*sin(th)*t-4.9*t.^2;
fplot(x,y,[0,T])
hold off
axis equal
grid on
xlabel('x')
ylabel('y')
title('Tiro parabólico')

Referencias

Physics Challenge for Teachers and Students. Solution to November 2010 Challenge. A Natural Log Puzzle. The Physics Teacher, Vol 49, 2011, pp. 631-632

Indian National Physics Olympiad. Homi Bhabha Centre for Science Eduaction. Solved papers NSEP & INPhO, 2016-2018, Example 30, pp. 25-26