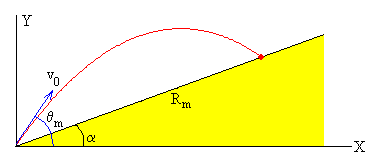
Alcance máximo en un plano inclinado
Se dispara un proyectil desde el origen con velocidad inicial v0, haciendo un ángulo θ con la horizontal, el punto de impacto está situado en un plano inclinado que forma un ángulo α con la horizontal. Para describir el movimiento establecemos un sistema de referencia como se indica en la figura.
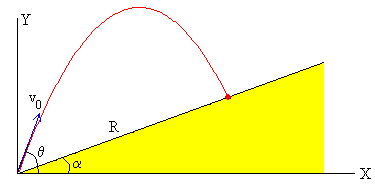
Las componentes de la velocidad del proyectil en función del tiempo son:
vx=v0·cosθ
vy=v0·sinθ-g·t
La posición en función del tiempo es
x= v0·cosθ·t
y= v0·sinθ·t-g·t2/2
Estas son las ecuaciones paramétricas de la trayectoria, ya que dado el tiempo t, se obtiene la posición x e y del proyectil.
Como las coordenadas x e y del punto de impacto están relacionadas por y=x·tanα, despejamos el tiempo de vuelo t, de las ecuaciones paramétricas de la trayectoria
El alcance R medido a lo largo del plano inclinado es
Cambio de Sistema de Referencia
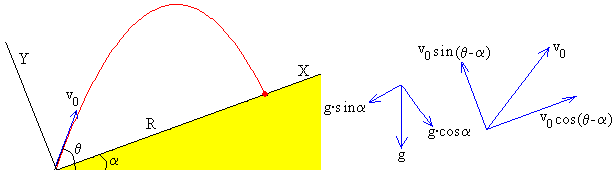
Analizamos el movimiento del proyectil en un Sistema de Referencia en el que el eje X es paralelo al plano inclinado y el eje Y es perpendicular al mismo.
La aceleración de la gravedad g está dirigida verticalmente hacia abajo. Las componentes de la aceleración de la gravedad y de la velocidad inicial se muestran en la figura. Las ecuaciones del movimiento del proyectil son
x=v0·cos(θ-α)·t-g·sinα·t2/2
y=v0·sin(θ-α)·t-g·cosα·t2/2
El tiempo de vuelo se determina poniendo y=0, y despejando el tiempo t.
Sustituimos el valor de t en la primera ecuación
v0=60; %velocidad de disparo
alfa=20*pi/180; %plano inclinado
x=(20:90)*pi/180;
R=2*v0^2*sin(x-alfa).*cos(x)/(9.8*cos(alfa)^2);
plot(x,R)
set(gca,'XTick',0:pi/8:pi/2)
set(gca,'XTickLabel',{'0','\pi/8','\pi/4','3\pi/8','\pi/2'})
grid on
xlabel('\theta')
ylabel('R')
title('Alcance')
En la figura, se representa el alcance R en función del ángulo de tiro θ, para un plano inclinado α=20º y una velocidad de disparo v0=60 m/s. El alcance máximo se produce para el ángulo 55º
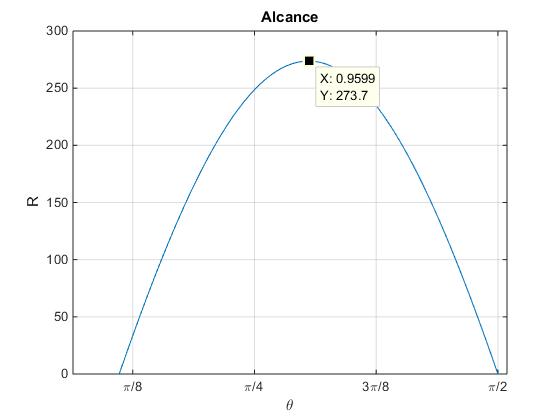
Alcance máximo
Derivando R con respecto del ángulo de tiro θ e igualando a cero obtenemos el ángulo de tiro θm para el cual el alcance es máximo.
El ángulo θ para el cual el alcance R es máximo vale
El alcance máximo sin cálculo de derivadas
Una forma alternativa de calcular el ángulo θm, sin tener que realizar un cálculo de derivadas es el siguiente:
Eliminamos el tiempo t, en de las ecuaciones paramétricas de la trayectoria, llegamos a la ecuación de la parábola (recuérdese que 1/cos2θ=1+tan2θ)
Las coordenadas x0 e y0 del punto de impacto están relacionadas y0=x0·tanα, llegamos a la siguiente ecuación de segundo grado en tanθ.
Las raíces de la ecuación de segundo grado son
Tenemos dos ángulos de tiro θ1 y el ángulo θ2 que dan lugar al mismo alcance R<Rm, tal como apreciamos en la figura.
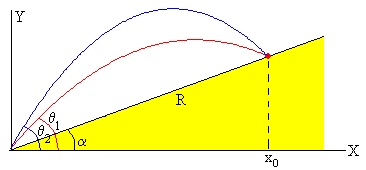
v0=60; %velocidad de disparo
R=200; %alcance
alfa=20*pi/180; %plano inclinado
x0=R*cos(alfa);
%ángulos de tiro
dis=1-2*9.8*x0*tan(alfa)/v0^2-(9.8*x0/v0^2)^2;
tan_1=v0^2*(1+sqrt(dis))/(9.8*x0);
tan_2=v0^2*(1-sqrt(dis))/(9.8*x0);
%trayectorias
x=linspace(0,x0,100);
y1=x*tan_1-9.8*x.^2*(1+tan_1^2)/(2*v0^2);
y2=x*tan_2-9.8*x.^2*(1+tan_2^2)/(2*v0^2);
hold on
plot(x,y1,'b',x,y2,'r')
%plano inclinado
xx=[0 250*cos(alfa) 250*cos(alfa)];
yy=[0 250*sin(alfa) 0];
fill(xx,yy,'y')
hold off
grid on
xlabel('x')
ylabel('y')
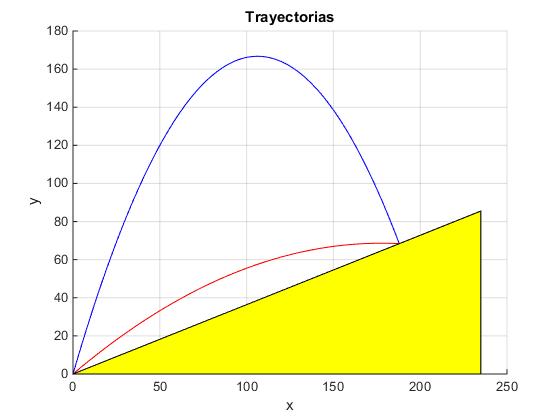
title('Trayectorias')
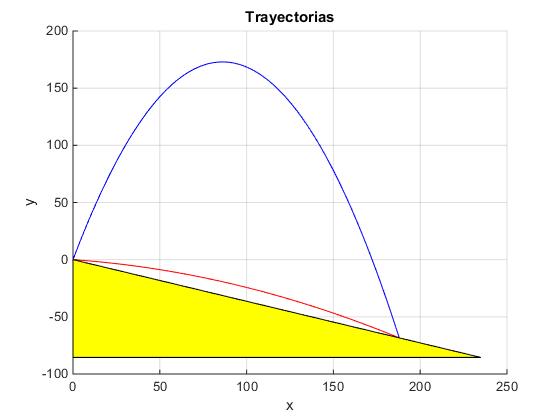
Modificamos el script para las pendientes negativas
v0=60; %velocidad de disparo
R=200; %alcance
alfa=-20*pi/180; %plano inclinado
x0=R*cos(alfa);
%ángulos de tiro
dis=1-2*9.8*x0*tan(alfa)/v0^2-(9.8*x0/v0^2)^2;
tan_1=v0^2*(1+sqrt(dis))/(9.8*x0);
tan_2=v0^2*(1-sqrt(dis))/(9.8*x0);
%trayectorias
x=linspace(0,x0,100);
y1=x*tan_1-9.8*x.^2*(1+tan_1^2)/(2*v0^2);
y2=x*tan_2-9.8*x.^2*(1+tan_2^2)/(2*v0^2);
hold on
plot(x,y1,'b',x,y2,'r')
%plano inclinado
xx=[0 0 250*cos(alfa)];
yy=[0 250*sin(alfa) 250*sin(alfa)];
fill(xx,yy,'y')
hold off
grid on
xlabel('x')
ylabel('y')
title('Trayectorias')
Empleamos las propiedades de las raíces de la ecuación de segundo grado ax2+bx+c=0
Haciendo algunas operaciones, relacionamos el ángulo θ1 y el ángulo θ2.
Cuando el alcance tiende hacia el valor máximo, los dos ángulos de tiro θ1 y θ2 se hacen cada vez más próximos hasta que coinciden. Las dos raíces son iguales θm=θ1=θ2.
Sustituyendo θm por α/2+π/4 en la expresión del alcance R al principio de la página
Otro modo de obtener el alcance máximo es el siguiente: el discriminante de la ecuación de segundo grado en tanθ, se hace cero, cuando la raíz es doble. Por tanto,
Despejamos Rm y sustituimos θm por α/2+π/4, obtenemos después de realizar algunas operaciones la misma expresión para Rm.
El tiempo de vuelo del proyectil para el ángulo θm vale
Simplificamos esta expresión hasta llegar a
Velocidad final y velocidad inicial
El ángulo que forma la velocidad final con el eje X es
Para el ángulo de disparo θm=π/4+α/2
El vector velocidad inicial y el vector velocidad final son perpendiculares.
Ejemplo
- La velocidad de disparo, v0=60 m/s
- La pendiente del plano inclinado, α=20º
- El ángulo de disparo, θ1=60º
-
El alcance vale
-
El ángulo de disparo θ1=50º
-
El ángulo para el cual el alcance es máximo (véase la última figura) es
-
Ángulos de tiro que producen el mismo alcance R=200 m.
El tiempo de vuelo vale
El alcance vale
El tiempo de vuelo vale
El alcance para este ángulo vale
El tiempo de vuelo es
Calculamos los dos ángulos de tiro que producen el mismo alcance R<Rm, por ejemplo un alcance de R=200 m. Calculamos las raíces de la ecuación de segundo grado en tanθ
x0=R·cosα, x0=200·cos20º=187.9 m
θ1=37.7º, θ2=72.3º, Como vemos θ1+θ2=90+20=110º, y θ1<θm<θ2
Alcance máximo, en general
En las secciones precedentes, el proyectil se dispara desde un punto situado en el plano inclinado. En esta sección, el proyectil se dispara desde un punto P que dista h del plano inclinado de ángulo α. Por comodidad, el ángulo de tiro θ se mide con el plano inclinado, no con el plano horizontal.
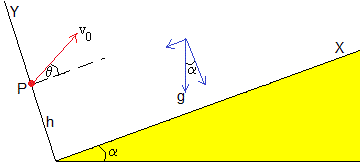
Establecemos los ejes X a lo largo del plano e Y perpendicular a dicho plano. Un proyectil se dispara con velocidad inicial v0 haciendo un ángulo θ con el eje X desde un punto P situado a una distancia h del plano inclinado.
El movimiento del proyectil es la composición de dos movimientos acelerados:
- a lo largo del eje X, con velocidad inicial v0cosθ y aceleración -g·sinα
- a lo largo del eje Y, con velocidad inicial v0sinθ y aceleración -g·cosα
El alcance x se obtiene para y=0.
Para obtener el alcance máximo, tenemos que resolver un problema de extremo condicionado
Dada la pendiente α, formamos la función de Lagrange
Escribimos el sistema de ecuaciones para determinar el parámetro λ y obtener los valores de las variables θ y t del extremo condicionado
De la primera ecuación, obtenemos
De la segunda ecuación,
De la tercera ecuación,
Tenemos que transformar esta ecuación en otra equivalente con el fin de despejar el ángulo θ+α en términos de μ y del ángulo α. Esta es
Comprobación
Llamamos x=tan(θ+α) y resolvemos la ecuación de segundo grado
Solamente es válida la raíz positiva
Casos particulares:
Plano horizontal, α=0
Se dispara desde un punto situado en el plano inclinado, h=0, μ=0
Resultado que hemos obtenido anteriormente. Recuérdese que ahora, el ángulo de tiro θ se mide con el plano inclinado
Comprobación
Ejemplo
Se dispara un proyectil con velocidad v0=60 m/s, desde un punto P que dista h=50 m del plano inclinado un ángulo α=20°
Calulamos el ángulo de tiro θm que hace que el alcance sea máximo
El resultado es θm=30.4°
Representamos tres trayectorias del proyectil para los ángulos de tiro: 25.4°, 30.4° y 35.4°. La trayectoria intermedia es la que tiene mayor alcance 305.7 m
v0=60; %velocidad de disparo
alfa=20*pi/180; %plano inclinado
h=50; %distancia a la posición de disparo
mu=2*h*9.8/v0^2;
th_m=atan((sin(alfa)+sqrt(1+mu*cos(alfa)))/(mu+cos(alfa)))-alfa;
disp(th_m*180/pi) %ángulo de tiro para el alcance máximo
hold on
plot(-h*sin(alfa),h*cos(alfa),'ro','markersize',4,'markerfacecolor','r')
line([0,-h*sin(alfa)],[0,h*cos(alfa)])
%plano inclinado
xx=[0 350*cos(alfa) 350*cos(alfa)];
yy=[0 350*sin(alfa) 0];
fill(xx,yy,'y')
%trayectorias
for th=[th_m-5*pi/180,th_m,th_m+5*pi/180] %trayectorias
tt=(v0*sin(th)+sqrt(v0^2*sin(th)^2+2*9.8*h*cos(alfa)))/(9.8*cos(alfa));
x=@(t) -h*sin(alfa)+v0*cos(th+alfa)*t;
y=@(t) h*cos(alfa)+v0*sin(th+alfa)*t-4.9*t.^2;
fplot(x,y,[0,tt])
disp(sqrt(x(tt)^2+y(tt)^2)) %alcance
end
hold off
axis equal
grid on
xlabel('x')
ylabel('y')
title('Alcance máximo')
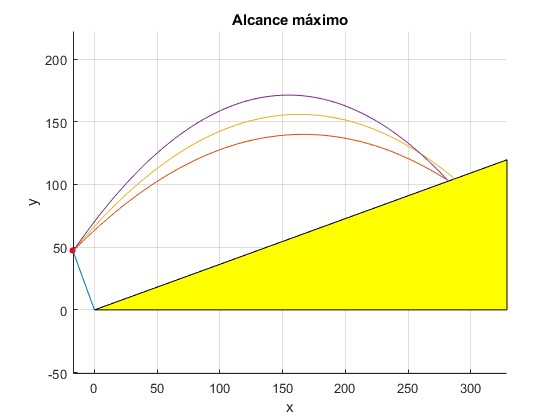
30.3557 %ángulo de tiro 300.7219 305.7106 %alcance máximo 300.4022
Referencias
Buckmaster H. A., Ideal ballistic trajectories revisited. Am. J. Phys. 53 (7) July 1985, pp. 638-641.
Drago Bajc. Maximum ranges in ideal projectile motion-A generalization. Am. J. Phys. 58 (4) April 1990, pp. 408-409

