Se dispara un proyectil con velocidad v₀ haciendo un ángulo θ con la horizontal. Las ecuaciones del movimiento son

${\displaystyle \{\begin{array}{l}{a}_x=0\\ a_y=-g\end{array}\{\begin{array}{l}{v}_x=v_0\cos \theta \\ v_y=v_0\text{sin}\theta -gt\end{array}\{\begin{array}{l}x=v_0\cos \theta t\\ y=v_0\text{sin}\theta t-\frac{1}{2}g{t}^2\end{array}}$

Eliminando el tiempo t obtenemos la ecuación de la trayectoria

${\displaystyle y=x\tan \theta -\frac{1}{2}\frac{g}{v_0^2{\cos }^2\theta }{x}^2}$

Alcance

La abscisa R del punto de impacto, denominada alcance se obtiene poniendo y=0 en la ecuación de la trayectoria

${\displaystyle R=\frac{2v_0^2\text{sin}\theta \cos \theta }{g}=\frac{v_0^2\text{sin(2}\theta )}{g}}$

El máximo valor de R se obtiene para θ=45º

Tiempo de vuelo

Poniendo y=0, y despejando t, tenemos dos soluciones t=0, que corresponde al disparo del proyectil y

${\displaystyle T=\frac{2v_0\text{sin}\theta }{g}}$

El valor máximo de T se obtiene para θ=90º. Cuando el proyectil se lanza verticalmente hacia arriba, describiendo una trayectoria rectilínea a lo largo del eje Y.

Área encerrada por la trayectoria y el eje horizontal X

En la figura, se muestra el área diferencial y·dx. El área total encerrada entre la trayectoria y el eje X se calcula mediante la integral definida.

${\displaystyle \begin{array}{l}A(\theta )={\displaystyle \underset{0}{\overset{R}{\int }}y·dx={\displaystyle \underset{0}{\overset{R}{\int }}\left(x\tan \theta -\frac{1}{2}\frac{g}{v_0^2{\cos }^2\theta }{x}^2\right)}}dx={\frac{1}{2}{x}^2\tan \theta -\frac{1}{2}\frac{g}{v_0^2{\cos }^2\theta }\frac{x^3}{3}|}_0^R=\\ \frac{1}{2}{R}^2\tan \theta -\frac{1}{2}\frac{g}{v_0^2{\cos }^2\theta }\frac{R^3}{3}=\frac{2}{3}\frac{v_0^4}{g^2}{\text{sin}}^3\theta \cos \theta \end{array}}$

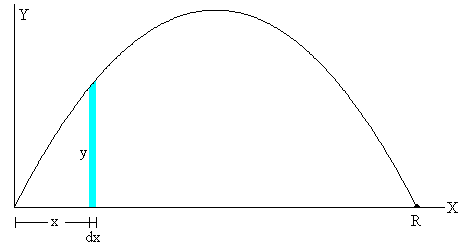
En la figura, se muestra que el comportamiento del área total A encerrada entre la trayectoria y el eje X con el ángulo de tiro θ. El área aumenta con el ángulo de tiro θ, alcanzando un máximo y luego vuelve a disminuir, hasta que se hace cero cuando θ=90º

f=@(x) (sin(x).^3).*cos(x);
fplot(f,[0,pi/2])
set(gca,'XTick',0:pi/12:pi/2)
set(gca,'XTickLabel',{'0','\pi/12','\pi/6','\pi/4','\pi/3','5\pi/12','\pi/2'})
grid on
xlabel('\theta')
ylabel('Area')
title('Area encerrada por la trayectoria')

Calculamos el máximo de la función f(θ)=sin³θ·cosθ

${\displaystyle \frac{df}{d\theta }={\text{sin}}^2\theta (3{\cos }^2\theta -{\text{sin}}^2\theta )=0\text{tan}\theta =\pm \sqrt{3}}$

Tiene sentido solamente el signo positivo, que corresponde al ángulo de tiro θ=60º

Cuando se dispara un proyectil con un ángulo de tiro θ=60º, el área encerrada por la trayectoria y el eje horizontal X es máxima.

Longitud de la trayectoria

La longitud del elemento diferencial de la trayectoria (en color rojo en la figura) es la hipotenusa de un triángulo rectángulo cuyos catetos tienen longitudes dx y dy, respectivamente.

${\displaystyle \sqrt{d{x}^2+d{y}^2}={\sqrt{1+\left(\frac{dy}{dx}\right)}}^{2}dx}$

La longitud total del camino recorrido por el proyectil es

${\displaystyle L(\theta )={\displaystyle \underset{0}{\overset{R}{\int }}\sqrt{d{x}^2+d{y}^2}={\displaystyle \underset{0}{\overset{R}{\int }}\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}dx}=}{\displaystyle \underset{0}{\overset{R}{\int }}\sqrt{1+{\left(-\frac{g}{v_0^2{\cos }^2\theta }x+\tan \theta \right)}^2}dx}}$

Esta integral es de la forma

${\displaystyle {\displaystyle \int \sqrt{1+u^2}}du=\frac{u}{2}\sqrt{u^2+1}+\frac{1}{2}\ln \left|u+\sqrt{u^2+1}\right|}$

>> syms x;
>> int(sqrt(1+x^2),x)
ans =asinh(x)/2 + (x*(x^2 + 1)^(1/2))/2

El arco seno hiperbólico se define

${\displaystyle \text{asinh}(x)=\ln \left(x+\sqrt{x^2+1}\right)}$

La longitud del camino es

${\displaystyle L(\theta )=-\frac{v_0^2{\cos }^2\theta }{g}{\displaystyle \underset{u_0}{\overset{u_1}{\int }}\sqrt{1+u^2}du}u=\frac{-g}{v_0^2{\cos }^2\theta }x+\tan \theta }$

Al cambiar la variable de x a u cambian los límites de la integral.

• El límite inferior se obtiene para x=0, es decir, para u₀=tanθ
• El límite superior se obtiene para x=R, es decir, para u₁=-tanθ

$$\begin{gathered} {\displaystyle L(\theta )=-\frac{v_0^2{\cos }^2\theta }{g}{\displaystyle \underset{u_0}{\overset{u_1}{\int }}\sqrt{1+u^2}du}= \\ -\frac{v_0^2{\cos }^2\theta }{g}\left\{\begin{array}{l}\left(\frac{-\tan \theta }{2}\sqrt{1+{\tan }^2\theta }+\frac{1}{2}\ln \left|-\tan \theta +\sqrt{1+{\tan }^2\theta }\right|\right)\\ -\left(\frac{\tan \theta }{2}\sqrt{1+{\tan }^2\theta }+\frac{1}{2}\ln \left|\tan \theta +\sqrt{1+{\tan }^2\theta }\right|\right)\end{array}\right\}} \end{gathered}$$

Teniendo en cuenta que 1+tan²θ=1/cos²θ

${\displaystyle \begin{array}{l}L(\theta )=-\frac{v_0^2{\cos }^2\theta }{g}\left\{-\frac{\text{sin}\theta }{{\cos }^2\theta }+\frac{1}{2}\ln \left(\frac{1-\text{sin}\theta }{\cos \theta }\right)-\frac{1}{2}\ln \left(\frac{1+\text{sin}\theta }{\cos \theta }\right)\right\}=\\ -\frac{v_0^2{\cos }^2\theta }{g}\left\{-\frac{\text{sin}\theta }{{\cos }^2\theta }+\frac{1}{2}\ln \left(\frac{1-\text{sin}\theta }{1+\text{sin}\theta }\right)\right\}=-\frac{v_0^2{\cos }^2\theta }{g}\left\{-\frac{\text{sin}\theta }{{\cos }^2\theta }+\frac{1}{2}\ln \left(\frac{1-{\text{sin}}^{\text{2}}\theta }{{(1+\text{sin}\theta )}^2}\right)\right\}=\\ -\frac{v_0^2{\cos }^2\theta }{g}\left\{-\frac{\text{sin}\theta }{{\cos }^2\theta }-\ln \left(\frac{1+\text{sin}\theta }{\cos \theta }\right)\right\}=\frac{v_0^2}{g}\left\{\text{sin}\theta +{\cos }^2\theta \ln \left(\frac{1+\text{sin}\theta }{\cos \theta }\right)\right\}\end{array}}$

En la figura, se muestra que el comportamiento de la longitud L del camino recorrido por el proyectil con el ángulo de tiro θ. La longitud aumenta con el ángulo de tiro θ, alcanzando un máximo y luego vuelve a disminuir.

f=@(x) sin(x)+(cos(x).^2).*log((1+sin(x))./cos(x));
fplot(f,[0,pi/2])
set(gca,'XTick',0:pi/12:pi/2)
set(gca,'XTickLabel',{'0','\pi/12','\pi/6','\pi/4','\pi/3','5\pi/12','\pi/2'})
grid on
xlabel('\theta')
ylabel('Longitud')
title('Longitud del camino recorrido por el proyectil')

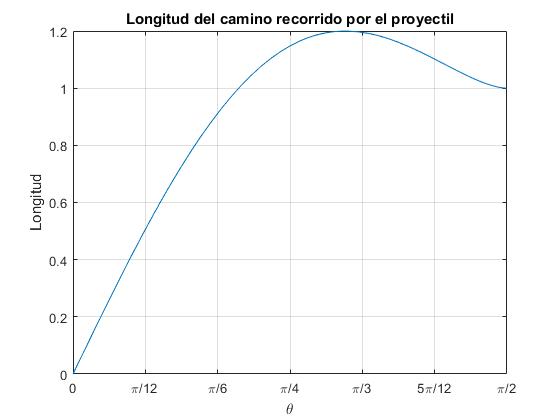
Derivamos L(θ) para hallar el ángulo θ para el cual la longitud de la trayectoria es máxima

${\displaystyle \frac{dL}{d\theta }=2\frac{v_0^2}{g}\cos \theta \left(1-\text{sin}\theta \ln \left(\frac{1+\text{sin}\theta }{\cos \theta }\right)\right)=0}$

Tenemos que resolver la ecuación trascendente

${\displaystyle 1-\text{sin}\theta \ln \left(\frac{1+\text{sin}\theta }{\cos \theta }\right)=0}$

La representación gráfica nos indica que el máximo de L(θ) se encuentra entre 50 y 60º. Se calcula la raíz de la ecuación trascendente con fzero. El valor que se obtiene es θ_m=56.46º

>> f=@(x) 1-sin(x)*log((1+sin(x))/cos(x));
>> fzero(f,50*pi/180,60*pi/180)*180/pi
ans =   56.4658

Velocidad media

La velocidad media de una partícula que se mueve, es el cociente entre la distancia total L y el tiempo T empleado en recorrerla.

${\displaystyle \langle v\rangle =\frac{L}{T}}$

Hemos calculado la longitud de la trayectoria de un proyectil disparado con velocidad v₀ y ángulo de tiro θ

${\displaystyle L(\theta )=\frac{v_0^2}{g}\left\{\sin \theta +{\cos }^2\theta \ln \left(\frac{1+\sin \theta }{\cos \theta }\right)\right\}}$

La velocidad media es

${\displaystyle \langle v\rangle \left(\theta \right)=\frac{L(\theta )}{\frac{2v_0\sin \theta }{g}}=\frac{v_0}{2}\left\{1+\frac{{\cos }^2\theta }{\sin \theta }\ln \left(\frac{1+\sin \theta }{\cos \theta }\right)\right\}}$

Tenemos dos casos especiales, cuando θ→0 y cuando θ→π/2

La primera tarea es prescindir de los términos cuyo resultado ya conocemos

• Cuando θ→0

El término

${\displaystyle \frac{1}{\sin \theta }\ln \left(\frac{1+\sin \theta }{\cos \theta }\right)}$

produce una indeterminación del tipo 0/0. Aplicamos la regla de L'Hôpital

${\displaystyle \begin{array}{l}\underset{x\to a}{\lim }\frac{f(x)}{g(x)}=\underset{x\to a}{\lim }\frac{f\text{'}(x)}{g\text{'}(x)}\hfill \\ \begin{array}{l}\{\begin{array}{l}f\left(\theta \right)=\ln \left(\frac{1+\sin \theta }{\cos \theta }\right)\\ g\left(\theta \right)=\sin \theta \end{array}\\ \frac{df}{d\theta }=\frac{\frac{{\cos }^2\theta +\sin \theta \left(1+\sin \theta \right)}{{\cos }^2\theta }}{\frac{1+\sin \theta }{\cos \theta }}=\frac{1}{\cos \theta }\\ \frac{\frac{df}{d\theta }}{\frac{dg}{d\theta }}=\frac{\frac{1}{\cos \theta }}{\cos \theta }=\frac{1}{{\cos }^2\theta }\\ \underset{\theta \to 0}{\lim }\left(\frac{1}{{\cos }^2\theta }\right)=1\end{array}\hfill \end{array}}$

El resultado es, $\langle v\rangle \left(0\right)=v_0$

• Cuando θ→π/2

${\displaystyle {\cos }^2\theta \ln \left(\frac{1+\sin \theta }{\cos \theta }\right)={\cos }^2\theta \ln \left(1+\sin \theta \right)-{\cos }^2\theta \ln \left(\cos \theta \right)}$

El término

${\displaystyle {\cos }^2\theta \ln \left(\cos \theta \right)}$

produce una indeterminación del tipo 0·∞

${\displaystyle \underset{x\to \frac{\pi }{2}}{\lim }\left({\cos }^2\theta ·\ln \left(\cos \theta \right)\right)=\underset{x\to \frac{\pi }{2}}{\lim }\frac{\ln \left(\cos \theta \right)}{\frac{1}{{\cos }^2\theta }}=\underset{x\to \frac{\pi }{2}}{\lim }\left(\frac{\frac{-\sin \theta }{\cos \theta }}{\frac{-2\sin \theta }{{\cos }^3\theta }}\right)=\underset{x\to \frac{\pi }{2}}{\lim }\left(\frac{{\cos }^2\theta }{2}\right)=0}$

El resultado es $\langle v\rangle \left(\frac{\pi }{2}\right)=\frac{v_0}{2}$

Comprobamos con MATLAB

>> syms x;
>> y=cos(x)^2*log((1+sin(x))/cos(x))/sin(x);
>> limit(y,x,0)
ans =1
>> limit(y,x,pi/2)
ans =0

Otra forma de obtener la velocidad media de la función v(t)

El valor medo de una función f(x) en el intervalo [a,b] es

${\displaystyle \langle f\rangle =\frac{1}{b-a}{\displaystyle \underset{a}{\overset{b}{\int }}f(x)·dx}}$

La velocidad del proyectil es

${\displaystyle v=\sqrt{v_{0x}^2+v_{0y}^2}=\sqrt{v_0^2{\cos }^2\theta +{\left(v_0\sin \theta -gt\right)}^2}}$

El valor medio de esta velocidad desde el momento del disparo t=0, del proyectil hasta que llega al suelo y=0, durante el tiempo de vuelo T es

${\displaystyle \langle v\rangle =\frac{1}{T}{\displaystyle \underset{0}{\overset{T}{\int }}\sqrt{v_0^2{\cos }^2\theta +{\left(v_0\sin \theta -gt\right)}^2}·dt},T=\frac{2v_0\sin \theta }{g}}$

Para resolver la integral hacemos elcambio de variable

${\displaystyle \begin{array}{l}u=v_0\sin \theta -gt,du=-g·dt\\ \langle v\rangle =-\frac{1}{gT}{\displaystyle \underset{0}{\overset{T}{\int }}\sqrt{v_0^2{\cos }^2\theta +u^2}·dx}\end{array}}$

Esta integral se ha resuelto en la página titulada Integrales, en el apartado 'Integración por sustitución'

${\displaystyle {{\displaystyle \int }}^{\text{}}\sqrt{a^2+x^2}dx=\frac{x}{2}\sqrt{a^2+x^2}+\frac{a^2}{2}\ln \left(x+\sqrt{a^2+x^2}\right)}$

Teniendo en cuenta este resultado

${\displaystyle \begin{array}{l}\langle v\rangle =-\frac{1}{gT}{\left(\frac{\left(v_0\sin \theta -gt\right)}{2}\sqrt{v_0^2{\cos }^2\theta +{\left(v_0\sin \theta -gt\right)}^2}+\frac{v_0^2{\cos }^2\theta }{2}\ln \left(\left(v_0\sin \theta -gt\right)+\sqrt{v_0^2{\cos }^2\theta +{\left(v_0\sin \theta -gt\right)}^2}\right)\right)|}_0^T=\\ -\frac{1}{gT}\left\{\begin{array}{l}\frac{\left(-v_0\sin \theta \right)}{2}\sqrt{v_0^2{\cos }^2\theta +{\left(-v_0\sin \theta \right)}^2}+\frac{v_0^2{\cos }^2\theta }{2}\ln \left(\left(-v_0\sin \theta \right)+\sqrt{v_0^2{\cos }^2\theta +{\left(-v_0\sin \theta \right)}^2}\right)-\\ \left(\frac{\left(v_0\sin \theta \right)}{2}\sqrt{v_0^2{\cos }^2\theta +{\left(v_0\sin \theta \right)}^2}+\frac{v_0^2{\cos }^2\theta }{2}\ln \left(\left(v_0\sin \theta \right)+\sqrt{v_0^2{\cos }^2\theta +{\left(v_0\sin \theta \right)}^2}\right)\right)\end{array}\right\}\\ -\frac{1}{gT}\left\{-\frac{v_0^2\sin \theta }{2}+\frac{v_0^2{\cos }^2\theta }{2}\ln \left(v_0-v_0\sin \theta \right)-\left(\frac{v_0^2\sin \theta }{2}+\frac{v_0^2{\cos }^2\theta }{2}\ln \left(v_0+v_0\sin \theta \right)\right)\right\}=\\ \frac{1}{2v_0\sin \theta }\left\{v_0^2\sin \theta +\frac{v_0^2{\cos }^2\theta }{2}\ln \left(\frac{1+\sin \theta }{1-\sin \theta }\right)\right\}\end{array}}$

La velocidad media es

${\displaystyle \langle v\rangle \left(\theta \right)=\frac{v_0}{2}\left\{1+\frac{{\cos }^2\theta }{2\sin \theta }\ln \left(\frac{1+\sin \theta }{1-\sin \theta }\right)\right\}}$

El resultado es el mismo que el obtenido previamente ya que

${\displaystyle \begin{array}{l}\frac{1}{2}\ln \left(\frac{1+\sin \theta }{1-\sin \theta }\right)=\ln \left(\frac{1+\sin \theta }{\cos \theta }\right)\\ \frac{1+\sin \theta }{1-\sin \theta }={\left(\frac{1+\sin \theta }{\cos \theta }\right)}^2\\ 1-{\sin }^2\theta ={\cos }^2\theta \end{array}}$

Velocidad media de la función v(y)

Hemos obtenido el valor medio de la función v(t) ahora, vamos a obtener el valor medio de la función v(y) desde y=0 hasta la altura máxima que alcanza el proyectil, y_m

${\displaystyle \begin{array}{l}\{\begin{array}{l}{v}_x=v_0\cos \theta \\ v_y=v_0\sin \theta -gt\end{array}\\ y=v_0\sin \theta ·t-\frac{1}{2}g{t}^2\\ v^2=v_x^2+v_y^2=v_0^2-2v_0\sin \theta ·gt+g^2{t}^2=v_0^2-2gy\end{array}}$

La altura máxima se alcanza cuando v_y=0

${\displaystyle y_m=\frac{v_0^2{\sin }^2\theta }{2g}}$

La expresión del módulo de la velocidad v en función de la altura y se obtiene rápidamente aplicando el principio de conservación de la energía

${\displaystyle \frac{1}{2}m{v}_0^2=\frac{1}{2}m{v}^2+mgy}$

La velocidad media

${\displaystyle \langle v\rangle =\frac{1}{y_m}{\displaystyle \underset{0}{\overset{y_m}{\int }}\sqrt{v_0^2-2gy}}·dy}$

Haciendo el cambio de variable

${\displaystyle \begin{array}{l}u=v_0^2-2gy,du=-2gdy\\ {\displaystyle \int \sqrt{v_0^2-2gy}}·dy=-\frac{1}{2g}{\displaystyle \int \sqrt{u}}·du=-\frac{1}{3g}{u}^{3/2}=-\frac{1}{3g}{\left(v_0^2-2gy\right)}^{3/2}\end{array}}$

El resultado es

${\displaystyle \begin{array}{l}\langle v\rangle =\frac{1}{3g{y}_m}\left\{-{\left(v_0^2-2g{y}_m\right)}^{3/2}+v_0^3\right\}=\frac{2}{3v_0^2{\sin }^2\theta }\left\{v_0^3-{\left(v_0^2-v_0^2{\sin }^2\theta \right)}^{3/2}\right\}\\ \langle v\rangle \left(\theta \right)=\frac{2v_0}{3{\sin }^2\theta }\left(1-{\cos }^3\theta \right)\end{array}}$

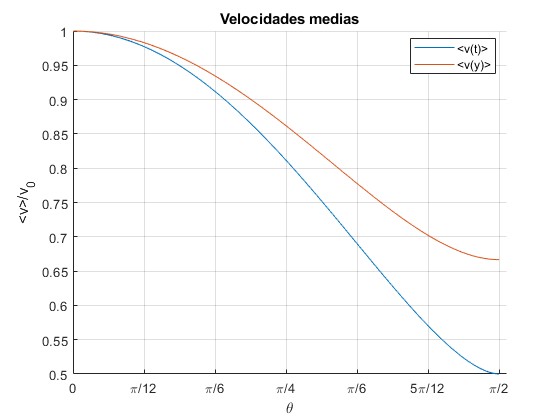
Representamos las velocidades medias <v>(θ)/v₀ de las funciones v(t) y v(y)

hold on
f=@(x) (1+cos(x).^2.*log((1+sin(x))./(1-sin(x)))./(2*sin(x)))/2;
fplot(f,[0,pi/2])
g=@(x) 2*(1-cos(x).^3)./(3*sin(x).^2);
fplot(g,[0,pi/2])
hold off
grid on
set(gca,'XTick',0:pi/12:pi/2)
set(gca,'XTickLabel',{'0','\pi/12','\pi/6','\pi/4','\pi/6','5\pi/12','\pi/2'})
xlabel('\theta')
legend('<v(t)>','<v(y)>','location', 'best')
ylabel('<v>/v_0')
title('Velocidades medias')

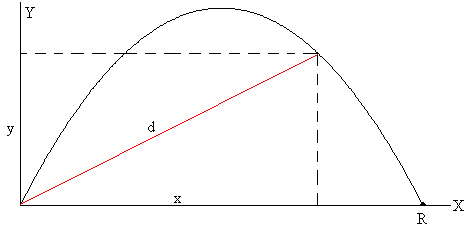
Distancia entre el origen del disparo y el proyectil

La distancia d entre el origen O y la posición (x, y) del proyectil en el instante t es

${\displaystyle d^2=x^2+y^2={\left(v_0\cos \theta ·t\right)}^2+{\left(v_0\text{sin}\theta ·t-\frac{1}{2}g{t}^2\right)}^2=\frac{1}{4}{g}^2{t}^4-v_{0}g\text{sin}\theta ·t^3+v_0^2{t}^2}$

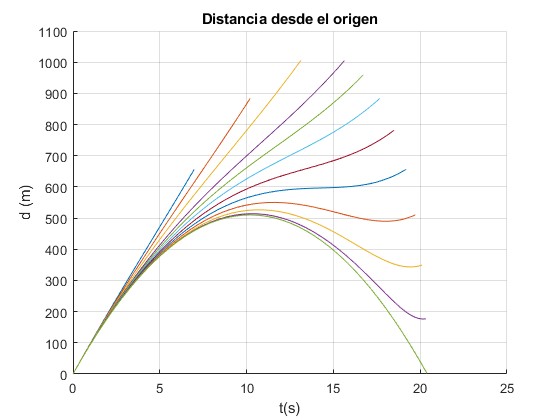
Representamos la distancia d en función del tiempo t para la velocidad de disparo v₀=100 m/s y los ángulo de tiro, θ=20, 30, 40, 50, 55, 60, 65, 70, 75, 80, 85, 90°. El tiempo T de vuelo es

${\displaystyle T=\frac{2v_0\sin \theta }{g}}$

v0=100; %velocidad de disparo
hold on
for th=[20,30,40,50,55,60,65,70,75,80,85,90]*pi/180
    T=2*v0*sin(th)/9.8; %tiempo de vuelo
    f=@(t) sqrt(v0^2*t.^2-v0*9.8*sin(th)*t.^3+9.8^2*t.^4/4);
    fplot(f,[0,T])
end
hold off
grid on
ylim([0,1100])
xlabel('t(s)')
ylabel('d (m)')
title('Distancia desde el origen')

El máximo de esta distancia se obtiene igualando la derivada con respecto al tiempo a cero

${\displaystyle g^2{t}^3-3v_{0}g\text{sin}\theta ·t^2+2v_0^{2}t=0}$

Simplificando entre t, calculamos las raíces de la ecuación de segundo grado en t.

${\displaystyle t_{\pm }=\frac{3v_0\text{sin}\theta }{2g}\left(1\pm \sqrt{1-\frac{8}{9{\text{sin}}^2\theta }}\right)}$

Las raíces reales existen cuando el radicando es positivo o nulo

${\displaystyle \frac{8}{9{\text{sin}}^2\theta }\le 1{\text{sin}}^2\theta \ge \frac{8}{9}{\theta }_0\ge 70.5º}$

Para ángulos de tiro θ<θ₀ la distancia d entre el origen y el proyectil es una función creciente del tiempo, que alcanza su máximo valor cuando impacta en el suelo.

El máximo d es igual al alcance R y ocurre en el instante T=2v₀sinθ/g que es el tiempo de vuelo.

En el instante t₊ la distancia d₊ entre el origen y la posición del proyectil vale

${\displaystyle \begin{array}{l}{d}_{+}^2=t_{+}^2\left(\frac{1}{4}{g}^2{t}_{+}^2-v_{0}g\text{sin}\theta ·t_{+}+v_0^2\right)=\\ {\left(\frac{3v_0\text{sin}\theta }{2g}\right)}^2{\left(1+\sqrt{1-\frac{8}{9{\text{sin}}^2\theta }}\right)}^2\left\{\begin{array}{l}\frac{1}{4}{g}^2{\left(\frac{3v_0\text{sin}\theta }{2g}\right)}^2{\left(1+\sqrt{1-\frac{8}{9{\text{sin}}^2\theta }}\right)}^2-\\ v_{0}g\text{sin}\theta \left(\frac{3v_0\text{sin}\theta }{2g}\right)\left(1+\sqrt{1-\frac{8}{9{\text{sin}}^2\theta }}\right)+v_0^2\end{array}\right\}=\\ v_0^2{\left(\frac{3v_0\text{sin}\theta }{2g}\right)}^2{\left(1+\sqrt{1-\frac{8}{9{\text{sin}}^2\theta }}\right)}^2\left\{-\frac{3}{8}{\text{sin}}^2\theta -\frac{3}{8}{\text{sin}}^2\theta \sqrt{1-\frac{8}{9{\text{sin}}^2\theta }}+\frac{1}{2}\right\}=\\ \frac{9v_0^4{\text{sin}}^{\text{2}}\theta }{4g^2}\left\{2-\frac{3}{2}{\text{sin}}^2\theta -\frac{4}{9{\text{sin}}^2\theta }+\left(\frac{4}{3}-\frac{3}{2}{\text{sin}}^2\theta \right)\sqrt{1-\frac{8}{9{\text{sin}}^2\theta }}\right\}\end{array}}$

En el instante t_- la distancia d_- entre el origen y el proyectil vale

${\displaystyle \begin{array}{l}{d}_{-}^2=t_{-}^2\left(\frac{1}{4}{g}^2{t}_{-}^2-v_{0}g\text{sin}\theta ·t_{-}+v_0^2\right)=\\ {\left(\frac{3v_0\text{sin}\theta }{2g}\right)}^2{\left(1-\sqrt{1-\frac{8}{9{\text{sin}}^2\theta }}\right)}^2\left\{\begin{array}{l}\frac{1}{4}{g}^2{\left(\frac{3v_0\text{sin}\theta }{2g}\right)}^2{\left(1-\sqrt{1-\frac{8}{9{\text{sin}}^2\theta }}\right)}^2-\\ v_{0}g\text{sin}\theta \left(\frac{3v_0\text{sin}\theta }{2g}\right)\left(1-\sqrt{1-\frac{8}{9{\text{sin}}^2\theta }}\right)+v_0^2\end{array}\right\}=\\ v_0^2{\left(\frac{3v_0\text{sin}\theta }{2g}\right)}^2{\left(1-\sqrt{1-\frac{8}{9{\text{sin}}^2\theta }}\right)}^2\left\{-\frac{3}{8}{\text{sin}}^2\theta +\frac{3}{8}{\text{sin}}^2\theta \sqrt{1-\frac{8}{9{\text{sin}}^2\theta }}+\frac{1}{2}\right\}=\\ \frac{9v_0^4{\text{sin}}^{\text{2}}\theta }{4g^2}\left\{2-\frac{3}{2}{\text{sin}}^2\theta -\frac{4}{9{\text{sin}}^2\theta }+\left(-\frac{4}{3}+\frac{3}{2}{\text{sin}}^2\theta \right)\sqrt{1-\frac{8}{9{\text{sin}}^2\theta }}\right\}\end{array}}$

Comprobamos que

${\displaystyle \begin{array}{l}{d}_{-}^2>d_{+}^2\\ \left\{2-\frac{3}{2}{\text{sin}}^2\theta -\frac{4}{9{\text{sin}}^2\theta }+\left(-\frac{4}{3}+\frac{3}{2}{\text{sin}}^2\theta \right)\sqrt{1-\frac{8}{9{\text{sin}}^2\theta }}\right\}>\\ \left\{2-\frac{3}{2}{\text{sin}}^2\theta -\frac{4}{9{\text{sin}}^2\theta }+\left(\frac{4}{3}-\frac{3}{2}{\text{sin}}^2\theta \right)\sqrt{1-\frac{8}{9{\text{sin}}^2\theta }}\right\}\\ \left(-\frac{4}{3}+\frac{3}{2}{\text{sin}}^2\theta \right)>\left(\frac{4}{3}-\frac{3}{2}{\text{sin}}^2\theta \right)\\ {\text{sin}}^2\theta >\frac{8}{9}\end{array}}$

De las dos soluciones de la ecuación de segundo grado t₊ y t_- solamente hemos de tener en cuenta la segunda, ya que d_->d₊ para θ>θ₀=70.5º .

Verificamos que el instante t_- es menor que el tiempo de vuelo T

${\displaystyle \frac{t_{-}}{T}=\frac{\frac{3v_0\text{sin}\theta }{2g}\left(1-\sqrt{1-\frac{8}{9{\text{sin}}^2\theta }}\right)}{\frac{2v_0}{g}\text{sin}\theta }=\frac{3}{4}\left(1-\sqrt{1-\frac{8}{9{\text{sin}}^2\theta }}\right)<1}$

Comparamos ahora d_- con el alcance R. Vamos a determinar el ángulo θ₁ a partir del cual d_- es mayor que  R

${\displaystyle \begin{array}{l}\frac{9v_0^4{\text{sin}}^{\text{2}}\theta }{4g^2}\left\{2-\frac{3}{2}{\text{sin}}^2\theta -\frac{4}{9{\text{sin}}^2\theta }+\left(-\frac{4}{3}+\frac{3}{2}{\text{sin}}^2\theta \right)\sqrt{1-\frac{8}{9{\text{sin}}^2\theta }}\right\}>{\left(\frac{2v_0^2\text{sin}\theta \cos \theta }{g}\right)}^2\\ \frac{2}{9}+\frac{5}{18}{\text{sin}}^2\theta -\frac{4}{9{\text{sin}}^2\theta }>\left(\frac{4}{3}-\frac{3}{2}{\text{sin}}^2\theta \right)\sqrt{1-\frac{8}{9{\text{sin}}^2\theta }}\\ {\left(\frac{2}{9}+\frac{5}{18}{\text{sin}}^2\theta -\frac{4}{9{\text{sin}}^2\theta }\right)}^2>{\left(\frac{4}{3}-\frac{3}{2}{\text{sin}}^2\theta \right)}^2\left(1-\frac{8}{9{\text{sin}}^2\theta }\right)\\ {\text{11sin}}^8\theta -31{\text{sin}}^6\theta +28{\text{sin}}^4\theta -7{\text{sin}}^2\theta -1>0\end{array}}$

La ecuación

11x⁸-31x⁶+28x⁴-7x²-1=0

Tiene dos raíces reales dobles x=1 y x=-1

11x⁸-31x⁶+28x⁴-7x²-1=(x-1)² (x+1)²(11x⁴-9x²-1)

Resolvemos la ecuación bicuadrada

11x⁴-9x²-1=0 haciendo el cambio de variable z=x²

11z²-9z-1=0

La raíces reales son x=±0.95775, que corresponden al ángulo θ=±arcsinx=±73.3º

Para el ángulo θ≥θ₁=73.3º la distancia d_- entre le origen y la posición del proyectil en el instante t_- es mayor que el alcance R

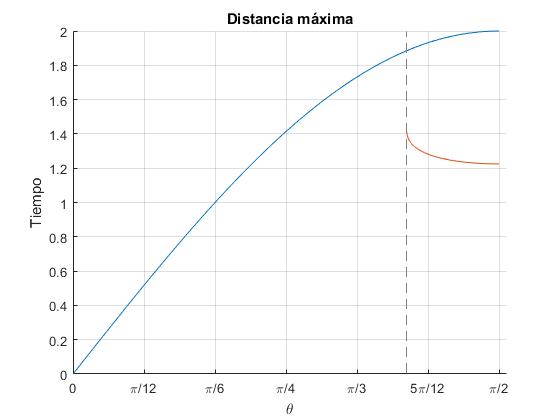
En la figura se muestra, el instante t_m para el cual la distancia d entre el proyectil y el origen es máximo. Para θ<θ₁=73.3º esta distancia es el alcance R y el tiempo t_m=T al tiempo de vuelo. Sorprendentemente, la curva presenta una discontinuidad en θ=θ₁. A partir de este ángulo θ>θ₁, el instante t_m=t_- y la distancia máxima d_m=d_-. Las expresiones de t_- y d_- en función del ángulo de tiro θ las hemos deducido en este apartado.

t=@(x) (3*sin(x)/2).*sqrt(1-sqrt(1-8./(9*sin(x).^2)));
T=@(x) 2*sin(x);
hold on
fplot(T,[0,pi/2]); 
fplot(t,[0,pi/2]) 
hold off
set(gca,'XTick',0:pi/12:pi/2)
set(gca,'XTickLabel',{'0','\pi/12','\pi/6','\pi/4','\pi/3','5\pi/12','\pi/2'})
grid on
xlabel('\theta')
ylabel('Tiempo')
title('Distancia máxima')

La gráfica de color azul es proporcional al tiempo de vuelo T. La grafíca de color amarillo es proporcional a t_-. La segunda es menor que T en el intervalo (73.3°,90°)

Ejemplo:

• Sea θ=71º>70.5º.

El alcance vale

${\displaystyle R=\frac{v_0^2}{g}\text{sin(2}·71)=0.616·\frac{v_0^2}{g}}$

El tiempo de vuelo

${\displaystyle T=\frac{v_0}{g}2·\text{sin}71=1.891\frac{v_0}{g}}$

El valor máximo de la distancia d_m entre el origen y el proyectil se produce en el instante

${\displaystyle t_m=\frac{v_0}{g}\frac{3·\text{sin}71}{2}\left(1-\sqrt{1-\frac{8}{9·{\text{sin}}^{2}71}}\right)=1.311\frac{v_0}{g}}$

que es menor que el tiempo de vuelo T

Calculamos la posición del proyectil en el instante t_m

x_m=v₀·cosθ·t_m=0.427·v₀²/g
y_m= v₀·sinθ·t_m-gt_m²/2=0.380·v₀²/g

${\displaystyle d_m=\sqrt{x_m^2+y_m^2}=0.572\frac{v_0^2}{g}}$

que es menor que el alcance R. Luego, para un ángulo de disparo de 71º, la máxima distancia entre el origen y el proyectil se produce en el instante T cuando llega al suelo y es el alcance R.

• Sea θ=75º>θ₁=73.3º.

El alcance vale

${\displaystyle R=\frac{v_0^2}{g}\text{sin(2}·75)=0.5·\frac{v_0^2}{g}}$

El tiempo de vuelo

${\displaystyle T=\frac{v_0}{g}2·\text{sin}75=1.932\frac{v_0}{g}}$

El valor máximo de la distancia d_m entre el origen y el proyectil se produce en el instante

${\displaystyle t_m=\frac{v_0}{g}\frac{3·\text{sin}75}{2}\left(1-\sqrt{1-\frac{8}{9·{\text{sin}}^{2}75}}\right)=1.134\frac{v_0}{g}}$

que es menor que el tiempo de vuelo T

Calculamos la posición del proyectil en este instante

x_m=v₀·cosθ·t_m=0.293·v₀²/g
y_m= v₀·sinθ·t_m-gt_m²/2=0.452·v₀²/g

${\displaystyle d_m=\sqrt{x_m^2+y_m^2}=0.539\frac{v_0^2}{g}}$

que es mayor que el alcance R

Luego, para un ángulo de disparo de 75º, la máxima distancia entre el origen y el proyectil se produce en el instante t_m=1.134v₀/g y vale d_m=0.539·v₀²/g.

Actividades

Se introduce

• El ángulo de tiro, en el control titulado Ángulo
• La velocidad de disparo se ha fijado en v₀=60 m/s

Se pulsa el botón titulado Nuevo y a continuación ►. Pulsando en el botón pausa || nos aproximamos al momento en el que la distancia es máxima. Pulsando repetidamente el botón paso a paso >|, nos acercamos a dicho instante.

Cuando el ángulo de tiro θ>θ₁=73.3º. El programa interactivo calcula el instante t_m para el cual la distancia entre el proyectil y el origen es máxima. Se dibuja el segmento de color azul que une ambas posiciones y se muestra la distancia d en la parte superior

Referencias

Sarafian H. On projectile motion. The Physics Teacher. Vol 37, February 1999, pp. 86-88

Hu H, Yu J. Another look at projectile motion. The Physics Teacher Vol 38, October 2000, pp. 423

Mirabelli A. A new projectile problem and the attribution of continuity. Am. J. Phys. 54 (3) March 1986, pp. 278-27

Chloe T. Calderon, Pirooz Mohazzabi. Average Speed in Projectile Motion and in General Motion of a Particle. Journal of Applied Mathematics and Physics, 2018, 6, 1540-1548. http://www.scirp.org/journal/jamp