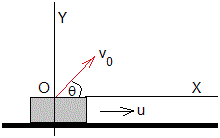
Supongamos que un vehículo que se mueve con velocidad u, dispara un proyectil con velocidad v₀ haciendo un ángulo de tiro θ con la horizontal. El efecto del movimiento del vehículo es reemplazar la componente v₀cosθ por u+v₀cosθ, de la velocidad inicial relativa a la Tierra.

Las ecuaciones del movimiento son:

${\displaystyle \overrightarrow{a}\{\begin{array}{l}{a}_x=0\\ a_y=-g\end{array}\overrightarrow{v}\{\begin{array}{l}{v}_x=u+v_0\cos \theta \\ v_y=v_0\sin \theta -gt\end{array}\overrightarrow{r}\{\begin{array}{l}x=(u+v_0\cos \theta )·t\\ y=v_0\sin \theta ·t-\frac{1}{2}g{t}^2\end{array}}$

El alcance del proyectil R, se obtiene cuando y=0.

${\displaystyle \begin{array}{l}t=\frac{2v_0\sin \theta }{g}\\ R=\left(u+v_0\cos \theta \right)\frac{2v_0\sin \theta }{g}\end{array}}$

El alcance máximo se obtiene derivando R con respecto al ángulo θ, e igualando a cero, dR/dθ=0

${\displaystyle \begin{array}{l}2{\cos }^2\theta +\frac{u}{v_0}\cos \theta -1=0\\ \cos \theta =\frac{1}{4}\left(\sqrt{k^2+8}-k\right)k=\frac{u}{v_0}\\ \sin \theta =\sqrt{1-{\cos }^2\theta }=\sqrt{\frac{1}{2}-\frac{k^2}{8}+\frac{k}{8}\sqrt{k^2+8}}\end{array}}$

Cuando k=u/v₀>0 es positivo el vehículo se mueve a lo largo del eje X hacia la derecha, cuando k<0, el vehículo se mueve hacia la izquierda

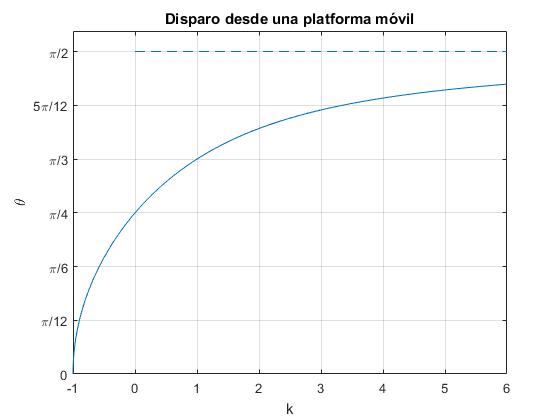
Representamos el ángulo θ en función de k. La asíntota horizontal cuando k→∞, es la recta θ=π/2, representada por una línea a trazos

f=@(k) acos((sqrt(k.^2+8)-k)/4);
fplot(f,[-1,6])
line([0,6],[pi/2,pi/2],'lineStyle','--')
set(gca,'YTick',0:pi/12:pi/2)
set(gca,'YTickLabel',{'0','\pi/12','\pi/6','\pi/4','\pi/3','5\pi/12','\pi/2'})
ylim([0,pi/2+.1])
grid on
xlabel('k')
ylabel('\theta')
title('Disparo desde una platforma móvil')

Sustituyendo sinθ y cosθ en el alcance R

${\displaystyle \begin{array}{l}R=\frac{2v_0^2}{g}\left(k+\cos \theta \right)\sin \theta \\ R_{max}=\frac{v_0^2}{2g}\left(3k+\sqrt{k^2+8}\right)\sqrt{\frac{1}{2}-\frac{k^2}{8}+\frac{k}{8}\sqrt{k^2+8}}\end{array}}$

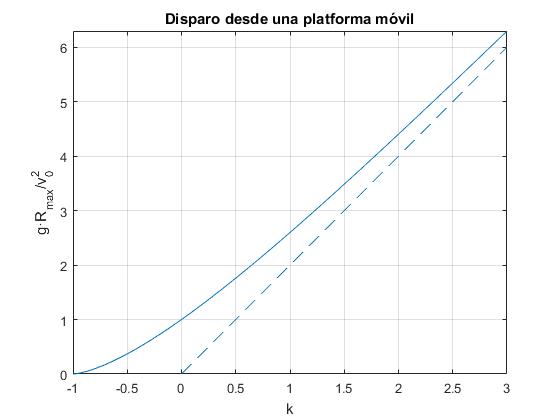
Representamos la función f(k), en el eje horizontal k=u/v₀ y en el eje vertical R_maxg/v². La línea a puntos representa el valor asintótico, cuando k→∞

f=@(k) (3*k+sqrt(k.^2+8)).*sqrt(1/2-k.^2/8+k.*sqrt(k.^2+8)/8)/2;
fplot(f,[-1,3])
line([0,3],[0,6], 'linestyle','--')
grid on
xlabel('k')
ylabel('g·R_{max}/v_0^2')
title('Disparo desde una platforma móvil')

Comprobamos que $\underset{k\to \infty }{\lim }\frac{f(k)}{k}=2$

>> syms k;
>> limit((3*k+sqrt(k^2+8))*sqrt(1/2-k^2/8+k*sqrt(k^2+8)/8)/(2*k),k,inf)
ans =2

La asíntota de la función f(k) es la recta y=2k

Ejemplo

El alcance máximo L de un proyectil disparado desde el suelo con velocidad v₀, se produce para el ángulo θ=45° y vale

${\displaystyle L=\frac{v_0^2\sin \left(2\theta \right)}{g}=\frac{v_0^2}{g}}$

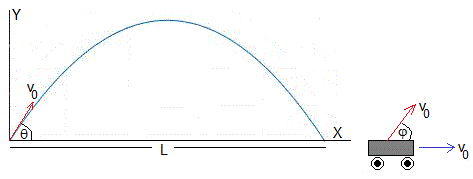
Supongamos que un vehículo se mueve con velocidad constante v₀ y dispara proyectiles con la misma velocidad v₀. El alcance máximo se produce para el ángulo φ tal que

${\displaystyle \cos \phi =\frac{1}{4}\left(\sqrt{k^2+8}-k\right),k=\frac{u}{v_0}}$

Como u=v₀, para k=1, cosφ=1/2, φ=π/3 (60°)

El alcance máximo R es

${\displaystyle \begin{array}{l}R=\frac{2v_0^2}{g}(k+\cos \phi )\sin \phi \hfill \\ R=\frac{2v_0^2}{g}\left(1+\frac{1}{2}\right)\frac{\sqrt{3}}{2}=\frac{3\sqrt{3}}{2}\frac{v_0^2}{g}=\frac{3\sqrt{3}}{2}L\hfill \end{array}}$

El vehículo se mueve a lo largo de un plano horizontal

Supongamos que un vehículo que se mueve con velocidad v_0x a lo largo de un plano horizontal sin rozamiento. Dispara un proyectil con velocidad inicial v_0y perpendicularmente a la dirección de la velocidad del vehículo tal como se muestra en la figura.

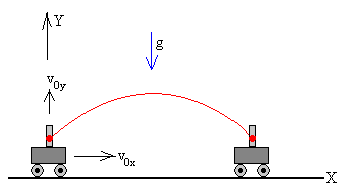
El proyectil se mueve a lo largo de un plano horizontal, a lo largo del eje X con velocidad constante v_0x. Su posición en el instante t es

x’=v_0x·t

La posición del proyectil en función del tiempo, es

x=v_0x·t
y=v_0y·t-gt²/2

Cuando el proyectil regresa al plano horizontal y=0, emplea un tiempo de

T=2v_0y/g

La distancia horizontal o alcance es

R=2v_0x·v_0y/g

Que es la misma distancia x’ que recorre el vehículo en el tiempo T. Luego, el vehículo dispara el proyectil en el origen y lo recoge a una distancia de R=2v_0x·v_0y/g

Ejemplo:

v_0x=15 m/s
v_0y=10 m/s

El tiempo T que tarda el proyectil en regresar la plano horizontal y el alcance R son

${\displaystyle T=\frac{2·10}{9.8}=2.04\text{s}R=\frac{2·15·10}{9.8}=30.6\text{m}}$

El vehículo recorre x’=30.6 m en el mismo tiempo

El vehículo asciende a lo largo de un plano inclinado

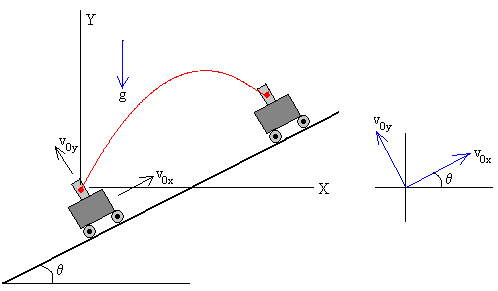
Supongamos que el vehículo asciende por un plano inclinado de ángulo θ.

Establecemos un sistema de referencia tal como se muestra en la figura, el eje X es horizontal y el eje Y es vertical. Calculamos las componentes X e Y de las velocidades iniciales. Las ecuación del movimiento del proyectil es la composición de dos movimientos: uniforme a lo largo del eje X y uniformemente acelerado a lo largo del eje Y

x=(v_0x·cosθ-v_0y·sinθ)·t
y=(v_0x·sinθ+v_0y·cosθ)·t-gt²/2

El punto de impacto se encuentra sobre el plano inclinado en la posición y=x·tanθ. Se despeja el tiempo t.

${\displaystyle T=\frac{2v_{0y}}{g·\cos \theta }}$

La distancia del origen al punto de impacto es

${\displaystyle R=\frac{x}{\cos \theta }=\frac{2v_{oy}}{g\cos \theta }\left(v_{0x}-v_{0y}·\tan \theta \right)}$

El vehículo se mueve a lo largo del plano inclinado. Si no hay rozamiento, la fuerza sobre el vehículo es la componente mg·sinθ del peso que es de sentido contrario a la velocidad v_0x. La ecuación del movimiento a lo largo del plano inclinado es

x’=v_0x·t-g·sinθ·t²/2

En el tiempo T que tarda el proyectil en chocar con el plano inclinado, se encuentra a una distancia R dada por la expresión anterior. El proyectil es disparado desde el vehículo en el origen en el instante t=0, y es recogido por el mismo vehículo en el instante T, cuando se encuentra a una distancia R del origen medida a lo largo del plano inclinado.

Como caso particular, mencionaremos aquél en el que el proyectil se mueve a lo largo del eje vertical Y. Cuando x=0, v_0x·cosθ-v_0y·sinθ=0, o bien

${\displaystyle \tan \theta =\frac{v_{0x}}{v_{0y}}}$

El proyectil parte del origen y regresa al mismo moviéndose hacia arriba y hacia abajo a lo largo del eje vertical Y.

Cambio de Sistema de Referencia

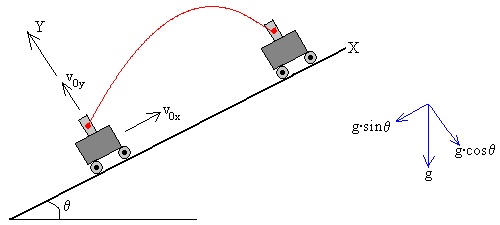
Analizamos el movimiento del vehículo y del proyectil en un Sistema de Referencia en el que el eje X es paralelo al plano inclinado y el eje Y es perpendicular al mismo.

La aceleración de la gravedad g está dirigida verticalmente hacia a bajo. Las componentes de la aceleración se muestran en la figura

Si su velocidad inicial del vehículo es v_0x. Su posición x’ en función del tiempo es

x’=v_0x·t-g·sinθ·t²/2

La posición del proyectil en función del tiempo respecto de estos ejes es la composición de dos movimientos uniformemente acelerados

x= v_0x·t-g·sinθ·t²/2
y=v_0y·t-gcosθ·t²/2

Cuando regresa al plano inclinado y=0, emplea un tiempo T y se encuentra a una distancia R del origen

${\displaystyle T=\frac{2v_{oy}}{g\cos \theta }R=\frac{2v_{oy}}{g\cos \theta }\left(v_{0x}-v_{0y}·\tan \theta \right)}$

El vehículo recorre la misma distancia x’ en el mismo tiempo t. El vehículo por tanto, dispara el proyectil en el origen y lo recoge a una distancia R dada por la fórmula anterior.

Cuando se cumple que

${\displaystyle \tan \theta =\frac{v_{0x}}{v_{0y}}}$

La partícula sale del origen y regresa al origen a lo largo de la dirección vertical. Para comprobarlo, en la expresión de x(t) de la posición del proyectil sustituimos v_0x por v_0y·tanθ, y multiplicamos ambos miembros por cosθ. Multiplicamos ambos miembros de la expresión y(t) de la posición del proyectil por sinθ. Verificamos que

x·cosθ=y·sinθ. Es decir, y=x/tanθ,  que es la ecuación de la recta vertical

Ejemplo:

θ=20º
v_0x=15 m/s
v_0y=10 m/s

El tiempo T que tarda el proyectil en regresar la plano horizontal y el alcance R valen

${\displaystyle T=\frac{2·10}{9.8·\cos 20}=2.17\text{s}R=\frac{2·10}{9.8·\cos 20}\left(15-10·\tan 20\right)=24.7\text{m}}$

El vehículo recorre x’=24.7 m en el mismo tiempo

Si la velocidad del vehículo v_0x=10·tan20=3.64 m/s el proyectil se mueve a lo largo de la dirección vertical. El proyectil sale y regresa al origen.

El vehículo desciende a lo largo de un plano inclinado

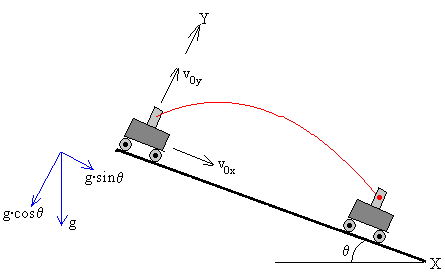
Supongamos que el vehículo desciende por un plano inclinado de ángulo θ.

Establecemos un Sistema de Referencia en el que el eje X es paralelo al plano inclinado y el eje Y es perpendicular al mismo

La aceleración de la gravedad g está dirigida verticalmente hacia a bajo. Las componentes de la aceleración se muestran en la figura

Si la velocidad inicial del vehículo es v_0x. Su posición x’ en función del tiempo es

x’=v_0x·t+g·sinθ·t²/2

La posición del proyectil en función del tiempo es

x= v_0x·t+g·sinθ·t²/2
y=v_0y·t-gcosθ·t²/2

Cuando regresa al plano inclinado y=0, emplea un tiempo T y se encuentra a una distancia R del origen  dados por

${\displaystyle T=\frac{2v_{oy}}{g\cos \theta }R=\frac{2v_{oy}}{g\cos \theta }\left(v_{0x}+v_{0y}·\tan \theta \right)}$

El vehículo recorre la misma distancia x’ en el mismo tiempo T. El vehículo por tanto, dispara el proyectil en el origen y lo recoge a una distancia de R dada por la fórmula anterior.

Ejemplo:

θ=20º
v_0x=15 m/s
v_0y=10 m/s

El tiempo T que tarda el proyectil en regresar la plano horizontal y el alcance R son

${\displaystyle T=\frac{2·10}{9.8·\cos 20}=2.17\text{s}R=\frac{2·10}{9.8·\cos 20}\left(15+10·\tan 20\right)=40.5\text{m}}$

El vehículo recorre x’=40.5 m en el mismo tiempo

Actividades

Se introduce

• El ángulo del plano inclinado, en el control titulado Angulo
• La velocidad inicial del vehículo, v_0x, en el control titulado Velocidad.
• La velocidad de disparo del proyectil desde el vehículo se ha fijado en v_0y=10 m/s

Se pulsa el botón titulado Nuevo

Se sugiere, describir el movimiento del proyectil en los dos Sistemas de Referencia:

• el eje X es horizontal y el eje Y es vertical.
• el eje X es paralelo al plano inclinado y el eje Y es perpendicular al mismo.

Referencias

Prigo R., Rosales A., More general and interesting versions of the ballistics cart and tunnel demostration. Am. J. Phys. 44 (8) August 1976, pp. 783-78

Physics Challenge for Teachers and Students. Let’s rock-n-roll!. The Physics Teacher. Vol. 53, September 2015. pp. 381