Se dispara un proyectil desde una altura h sobre un plano horizontal con velocidad inicial v₀, haciendo un ángulo θ con la horizontal. Para describir el movimiento establecemos un sistema de referencia como se indica en la figura.

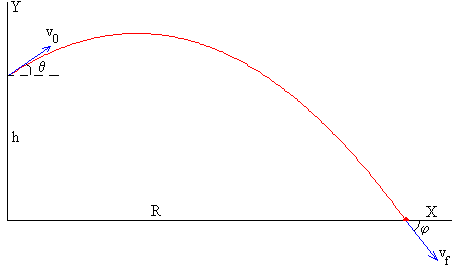
Las componentes de la velocidad del proyectil en función del tiempo son:

v_x=v₀·cosθ
v_y=v₀·sinθ-g·t

La posición del proyectil en función del tiempo es

x= v₀·cosθ·t
y= h+v₀·sinθ·t-g·t²/2

Estas son las ecuaciones paramétricas de la trayectoria, ya que dado el tiempo t, se obtiene la posición x e y del proyectil.

El tiempo de vuelo T se obtiene poniendo y=0 en la segunda ecuación y despejando el tiempo t.

${\displaystyle T=\frac{v_0}{g}\left(\text{sin}\theta +\sqrt{{\text{sin}}^2\theta +2z}\right)z=\frac{gh}{v_0^2}}$

El proyectil llega al punto de impacto en el instante t=T. Sustituyendo t en la primera ecuación obtenemos el alcance, o distancia horizontal entre el origen y el punto de impacto, R.

${\displaystyle R=\frac{v_0^2}{g}\left(\text{sin}\theta +\sqrt{{\text{sin}}^2\theta +2z}\right)\cos \theta z=\frac{gh}{v_0^2}}$

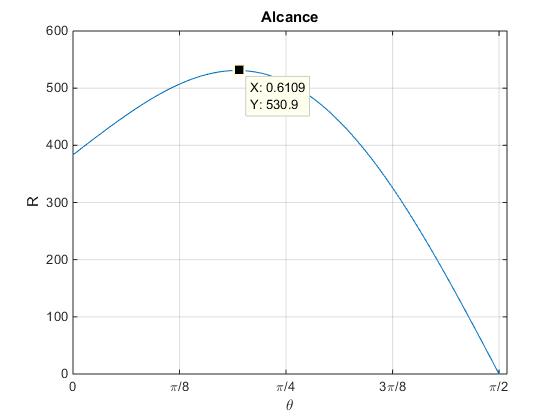
En la figura, se representa el alcance R en función del ángulo de tiro θ. Se ha señalado el ángulo 0.6109 rad=35° para el cual el alcance es máximo.

v0=60;
h=200;
x=(0:90)*pi/180;
R=v0^2*(sin(x)+sqrt(sin(x).^2+2*9.8*h/v0^2)).*cos(x)/9.8;
plot(x,R)
set(gca,'XTick',0:pi/8:pi/2)
set(gca,'XTickLabel',{'0','\pi/8','\pi/4','3\pi/8','\pi/2'})

grid on
xlabel('\theta')
ylabel('R')
title('Alcance')

La componente v_y de la velocidad cuando el cuerpo llega al suelo es

${\displaystyle v_y=v_0\text{sin}\theta -gT=-v_0\sqrt{{\text{sin}}^2\theta +2z}}$

La velocidad final v_f del proyectil cuando llega al suelo y el ángulo que forma con la horizontal (véase la primera figura) es

${\displaystyle \begin{array}{l}{v}_f=\sqrt{v_x^2+v_y^2}=v_0\sqrt{1+2z}\\ \tan \phi =\frac{v_y}{v_x}=-\frac{\sqrt{{\text{sin}}^2\theta +2z}}{\cos \theta }\end{array}}$

El módulo de la velocidad final v_f se puede calcular también, aplicando el principio de conservación de la energía.

${\displaystyle \frac{1}{2}m{v}_0^2+mgh=\frac{1}{2}m{v}_f^2}$

Alcance máximo

Derivando R con respecto del ángulo de tiro θ e igualando a cero obtenemos el ángulo de tiro θ_m para el cual el alcance es máximo.

${\displaystyle \begin{array}{l}\left(\cos \theta +\frac{2\text{sin}\theta \cos \theta }{2\sqrt{{\text{sin}}^2\theta +2z}}\right)\cos \theta -\left(\text{sin}\theta +\sqrt{{\text{sin}}^2\theta +2z}\right)\text{sin}\theta =0\\ \left({\cos }^2\theta -{\text{sin}}^2\theta \right)\left(\text{sin}\theta +\sqrt{{\text{sin}}^2\theta +2z}\right)=2z\text{sin}\theta \\ \sqrt{{\text{sin}}^2\theta +2z}=\frac{2z\text{sin}\theta }{\cos (2\theta )}-\text{sin}\theta \end{array}}$

Elevamos al cuadrado y simplificamos

${\displaystyle {\left(1-2·{\sin }^2\theta \right)}^2=2z·{\text{sin}}^2\theta -2·{\text{sin}}^2\theta \left(1-2·{\text{sin}}^2\theta \right)}$

${\displaystyle {\text{cos}}^2\theta =\frac{1+2z}{2+2z}{\text{sin}}^2\theta =\frac{1}{2+2z}}$

El ángulo θ_m para el cual el alcance R es máximo vale

${\displaystyle \tan {\theta }_m=\frac{1}{\sqrt{1+2z}}=\frac{v_0}{\sqrt{v_0^2+2gh}}}$

Sustituyendo cosθ y sinθ en función del parámetro z, en la expresión del alcance R, se obtiene después de algunas operaciones

${\displaystyle R_m=\frac{v_0^2}{g}\sqrt{1+2z}=\frac{v_0}{g}\sqrt{v_0^2+2gh}}$

Otra forma de expresar el alcance máximo R_m es

${\displaystyle R_m=\frac{v_0^2}{g·\tan {\theta }_m}}$

Llegamos a una expresión simple para el alcance máximo

R_m=h·tan(2θ_m)

El tiempo de vuelo T_m para el ángulo θ_m

${\displaystyle T_m=\frac{v_0}{g}\sqrt{2+2z}=\frac{\sqrt{2(v_0^2+2gh)}}{g}}$

El alcance máximo sin cálculo de derivadas

Una forma alternativa de calcular el ángulo θ_m, sin tener que realizar un cálculo de derivadas es el siguiente:

Eliminamos el tiempo t, en de las ecuaciones paramétricas de la trayectoria, llegamos a la ecuación de la parábola (recuérdese que 1/cos²θ=1+tan²θ)

${\displaystyle y=x\tan \theta -\frac{g{x}^2}{2v_0^2}(1+{\tan }^2\theta )}$

En el punto de impacto con el suelo y=0, obtenemos la ecuación de segundo grado en tanθ

${\displaystyle \frac{g{R}^2}{2v_0^2}{\tan }^2\theta -R·\tan \theta +\left(\frac{g{R}^2}{2v_0^2}-h\right)=0}$

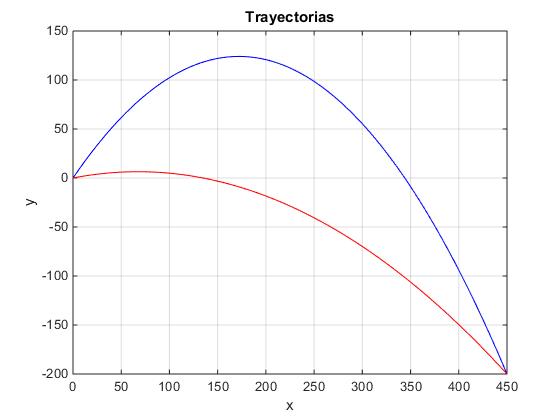
con dos soluciones para R<R_m, y una solución para R=R_m y ninguna para R>R_m,véase la figura.

v0=60;
h=200;
R=450;
%ángulos de tiro
a=9.8*R^2/(2*v0^2);
b=-R;
c=9.8*R^2/(2*v0^2)-h;
tan_1=(-b+sqrt(b^2-4*a*c))/(2*a);
tan_2=(-b-sqrt(b^2-4*a*c))/(2*a);
%trayectorias
x=linspace(0,R,100);
y1=x*tan_1-9.8*x.^2*(1+tan_1^2)/(2*v0^2);
y2=x*tan_2-9.8*x.^2*(1+tan_2^2)/(2*v0^2);
plot(x,y1,'b',x,y2,'r')
grid on
xlabel('x')
ylabel('y')
title('Trayectorias')

Esto implica que el discriminante de la ecuación de segundo grado debe ser cero para el ángulo θ_m  que hace que el alcance sea máximo

${\displaystyle R_m^2-4\frac{g{R}_m^2}{2v_0^2}\left(\frac{g{R}_m^2}{2v_0^2}-h\right)=0R_m=\frac{v_0}{g}\sqrt{2gh+v_0^2}}$

El mismo resultado que ya obtuvimos de una forma más laboriosa.

Velocidad final y velocidad inicial

La velocidad final y el ángulo que forma con el eje X son

${\displaystyle \begin{array}{l}{v}_f=v_0\sqrt{1+2z}\\ \tan {\phi }_m=-\frac{\sqrt{{\text{sin}}^2\theta +2z}}{\cos \theta }=-\sqrt{1+2z}\end{array}}$

La relación entre el ángulo de disparo θ_m y el ángulo φ_m que forma el vector velocidad cuando el proyectil llega al suelo es

${\displaystyle \tan {\phi }_m=-\frac{1}{\tan {\theta }_m}{\theta }_{\text{m}}={\phi }_m+\frac{\pi }{2}}$

El vector velocidad inicial $\overrightarrow{v_0}$ y el vector velocidad final $\overrightarrow{v_f}$ son perpendiculares,

Ejemplo:

• La velocidad de disparo, v₀=60 m/s,
• La altura inicial del proyectil, h=200 m
• El ángulo de tiro, θ=30º.

• El alcance R es

$$\begin{gathered} {\displaystyle z=\frac{9.8·200}{{60}^2}=0.\text{54} \\ R=\frac{{60}^2}{9.8}\left(\text{sin30º}+\sqrt{{\text{sin}}^{2}30º+2·0.54}\right)\cos 30º=527.2\text{m}} \end{gathered}$$

El tiempo T de vuelo del proyectil es

${\displaystyle T=\frac{60}{9.8}\left(\text{sin30º}+\sqrt{{\text{sin}}^{2}30º+2·0.54}\right)=\text{10}\text{.1}\text{s}}$

• El alcance máximo (véase la última figura) se obtiene para el ángulo

${\displaystyle \tan {\theta }_m=\frac{1}{\sqrt{1+2·0.54}}{\theta }_{\text{m}}=34.7º}$

El alcance y el tiempo de vuelo para este ángulo son, respectivamente

${\displaystyle \begin{array}{l}{R}_m=\frac{{60}^2}{9.8}\sqrt{1+2·0.54}=530.9\text{m}\\ T_m=\frac{60}{9.8}\sqrt{2+2·0.54}=10.8\text{s}\end{array}}$

• Ángulos de tiro que producen el mismo alcance R=450 m.

Calculamos los dos ángulos de tiro que producen el mismo alcance R<R_m, por ejemplo un alcance de R=450 m. Calculamos las raíces de la ecuación de segundo grado en tanθ. Véase la figura, más arriba

${\displaystyle \frac{9.8·{450}^2}{2·{60}^2}{\tan }^2\theta -450·\tan \theta +\left(\frac{9.8·{450}^2}{2·{60}^2}-200\right)=0}$

θ₁=10.8º, θ₂=55.3º,  Como vemos θ₁<θ_m<θ₂



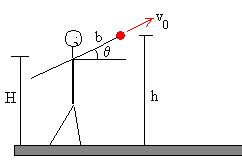
Supongamos que un atleta lanza un peso desde una altura h con una velocidad v₀, haciendo un ángulo θ con la horizontal.

Si el atleta lanza el peso desde una altura de h=2.1 m y quiere que llegue a una distancia R_m=22 m, el ángulo óptimo de lanzamiento θ_m vale

R_m=h·tan(2θ_m)     θ_m=42.3º

El análisis del lanzamiento del peso es más complicado, ya que la altura h no es independiente del ángulo θ, tal como se aprecia en la figura, sino que h=H+b·sinθ, siendo H la altura del hombro y b la longitud del brazo. (Véase De Luca 2005)

El salto de tarzán

Consideremos un objeto que denominaremos proyectil de masa m que cuelga de una cuerda de longitud l. Cuando se separa de su posición de equilibrio y se suelta comienza a oscilar, tal como estudiaremos en la página dedicada al péndulo simple.

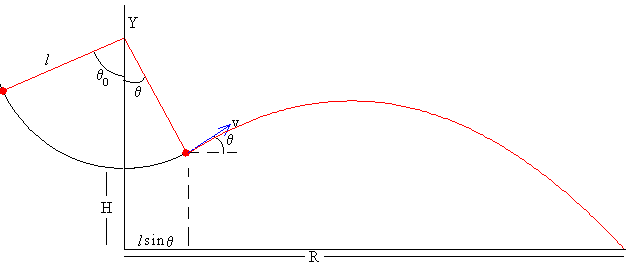
Soltamos el proyectil cuando la cuerda se desvía de la posición de equilibrio un ángulo θ₀. Se corta la cuerda cuando el péndulo se desvía de la posición vertical un ángulo θ<|θ₀|. El proyectil describe una trayectoria parabólica si se desprecia el rozamiento con el aire, tal como se aprecia en la figura.

Principio de conservación de la energía

El proyectil parte de la posición inicial θ₀, con velocidad inicial v=0. Describe un arco de circunferencia y llega a la posición final θ, con velocidad v.  Aplicamos el principio de conservación de la energía para calcular la velocidad v. Si ponemos el nivel cero de energía potencial en la parte más baja de la trayectoria

${\displaystyle \begin{array}{l}mg(l-l\cos {\theta }_0)=\frac{1}{2}m{v}^2+mg(l-l\cos \theta )\\ v=\sqrt{2gl(\cos \theta -\cos {\theta }_0)}\end{array}}$

Ecuaciones del tiro parabólico

Para describir el movimiento del proyectil, situamos los ejes X e Y del modo en el que se señala en la figura; el eje X en el suelo, y el eje Y tiene la dirección del péndulo en la posición de equilibrio θ=0.

El proyectil se dispara con una velocidad v, haciendo un ángulo θ con la horizontal, desde una altura h=H+(l-lcosθ). Siendo H+l la altura del centro de giro del péndulo.

La posición del proyectil en función del tiempo es

x= l·sinθ+v·cosθ·t
y= h+v·sinθ·t-g·t²/2

Siguiendo los mismos pasos que en la sección anterior. Obtenemos el alcance R, poniendo y=0, en la segunda ecuación, despejando el tiempo de vuelo t, y sustituyéndolo en la primera ecuación de la  trayectoria.

${\displaystyle R=\frac{v^2}{g}\left(\text{sin}\theta +\sqrt{{\text{sin}}^2\theta +2z}\right)\cos \theta +l·\text{sin}\theta z=\frac{gh}{v^2}}$

Expresamos el alcance R en función del ángulo θ

${\displaystyle R=2l(\cos \theta -\cos {\theta }_0)\cos \theta \left(\text{sin}\theta +\sqrt{{\text{sin}}^2\theta +\frac{H+l(1-\cos \theta )}{l(\cos \theta -\cos {\theta }_0)}}\right)+l·\text{sin}\theta }$

Dado el ángulo θ₀ de partida del objeto, se tratará de calcular el ángulo θ, para el cual el alcance R es máximo.

Alcance máximo

Dado el ángulo θ₀ de partida del objeto, calcularemos el ángulo θ_m, para el cual el alcance R es máximo.

l=0.6;
H=1.0;
aIni=80*pi/180;

x=linspace(0,aIni,100);
R=2*l*((cos(x)-cos(aIni)).*cos(x)).*(sin(x)+sqrt(sin(x).^2+
(H+l*(1-cos(x)))./(l*(cos(x)-cos(aIni)))))+l*sin(x);
plot(x,R)
set(gca,'XTick',0:pi/8:pi/2)
set(gca,'XTickLabel',{'0','\pi/8','\pi/4','3\pi/8','\pi/2'})

grid on
ylim([0 2])
xlabel('\theta')
ylabel('R')
title('Alcance')

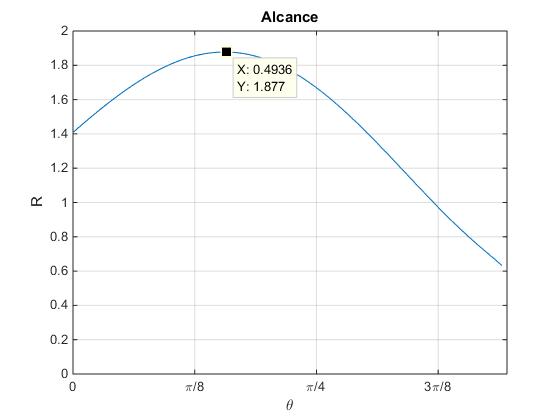
En la figura, se representa el alcance R en función del ángulo θ, para θ₀=80º. se ha señalado el ángulo para el cual se produce el alcance máximo, 0.4936 rad=28.3°.

El ángulo θ_m para el cual R es máximo se obtiene derivando R respecto del ángulo θ, e igualando a cero. Es decir,  resolviendo la ecuación dR/dθ=0.

En el segundo artículo citado en las referencias, el alcance máximo se obtiene calculando las raíces reales de la ecuación cúbica.

${\displaystyle x^3+\frac{H+l(1-2\cos {\theta }_0)}{l}{x}^2-\frac{H+l(1-\cos {\theta }_0)}{l}=0}$

con x=cosθ_m

Ejemplo:

• Longitud del péndulo, l=0.6 m
• Altura del proyectil en la situación de equilibrio, H=1.0 m
• Se desvía el péndulo θ₀=80º de la posición de equilibrio
• Se corta la cuerda cuando el péndulo se desvía θ=30º

La velocidad del proyectil cuando se corta la cuerda es

${\displaystyle v=\sqrt{2·9.8·0.6(\cos 30º-\cos 80º)}=2.85\text{m/s}}$

Ecuaciones del movimiento

x= 0.6·sin30+2.85·cos30·t
y= 1.0+0.6-0.6·cos30+2.85·sin30·t-9.8·t²/2

El alcance se calcula poniendo y=0. Resolvemos la ecuación de segundo grado en t. La raíz positiva vale t=0.64 s

Calculamos el alcance en la primera ecuación x=1.87 m

Calculamos el alcance de forma directa

$$\begin{gathered} {\displaystyle R=2·0.6(\cos 30-\cos 80)\cos 30\left(\text{sin30}+\sqrt{{\text{sin}}^{2}30+\frac{1.0+0.6(1-\cos 30)}{0.6(\cos 30-\cos 80)}}\right)+ \\ 0.6·\text{sin}30=1.87\text{m}} \end{gathered}$$

Para calcular el ángulo θ_m para el cual el alcance es máximo, se resuelve la ecuación cúbica

x³+a·x²+bx+c=0

con a=2.32, b=0, c=-2.49

Se calcula

${\displaystyle Q=\frac{a^2-3b}{9}=\text{0}\text{.60}R=\frac{2a^3-9ab+27c}{54}=-0.78}$

Como R²>Q³ entonces la ecuación tiene una raíz real

${\displaystyle \begin{array}{l}A=-\mathrm{sgn}(R){\left[\left|R\right|+\sqrt{R^2-Q^3}\right]}^{1/3}=1.12\\ x_1=A+\frac{Q}{A}-\frac{a}{3}=0.882\end{array}}$

El ángulo x₁=cosθ_m, θ_m=28.1º

Este ángulo θ_m se puede obtener aproximadamente de forma gráfica, tal como se ha señalado en la figura

H=1.0;
l=0.6;
aIni=80*pi/180;
a=(H+l*(1-2*cos(aIni)))/l;
c=-(H+l*(1-cos(aIni)))/l;
x=roots([1 a 0 c]);
for i=1:length(x)
    if isreal(x(i))
        disp(acos(x(i))*180/pi);
        break;
    end
end

28.0663

Actividades

Se introduce

• El ángulo θ₀ que se desvía el péndulo de la posición de equilibrio, en el control titulado Angulo inicial.

• El ángulo θ que forma el péndulo con la vertical cuando se corta la cuerda que sostiene el proyectil, en el control titulado Angulo final.

• La longitud del péndulo se ha fijado en l=0.6 m

• La altura del proyectil en la posición de equilibrio θ=0 se ha fijado en H=1.0 m

Se pulsa el botón titulado Nuevo.

Referencias

Buckmaster H. A., Ideal ballistic trajectories revisited. Am. J. Phys. 53 (7) July 1985, pp. 638-641.

Bittel D. Maximizing the range of a projectile launched by a simple pendulum. The Physics Teacher, 43, February 2005, pp. 98-100.

De Luca R. Shot-put kinematics. Eur. J. Phys. 26 (2005), pp. 1031-1036