Tiro parabólico y movimiento circular uniforme

Un paraguas de radio R está mojado y gira alrededor de su eje fijo con velocidad angular ω, en el plano vertical. Las gotas de agua se dispersan desde los extremos de las varillas con la misma velocidad v₀= ωR pero con distinta dirección. El vector velocidad inicial tiene una dirección tangente a la circunferencia tal como se muestra en la figura.

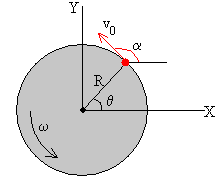
La gota de agua situada en la posición

x₀=R·cosθ
y₀=R·sinθ

se desprende del extremo de la varilla con una velocidad inicial v₀= ωR formando un ángulo α=θ+π/2 con la horizontal.

La posición de la gota de agua en función del tiempo es:

$\begin{array}{l} x = x_{0} + v_{0} \cos α \cdot t \\ y = y_{0} + v_{0} \sin α \cdot t - \frac{1}{2} g t^{2} \end{array}$

o bien,

$\begin{array}{l} x = R \cos θ - v_{0} \sin θ \cdot t \\ y = R \sin θ + v_{0} \cos θ \cdot t - \frac{1}{2} g t^{2} \end{array}$

R=1;  %radio del disco
h=8; %altura del disco
w=9.04; %velocidad angular de rotación

hold on
for ang=0:pi/6:2*pi
    %posición inicial
    x=R*cos(ang);
    y=R*sin(ang);
    plot(x,y,'o', 'markersize',3,'markeredgecolor','k',
'markerfacecolor','k')
    %tiempo de vuelo
    T=(w*R*cos(ang)+sqrt((w*R*cos(ang))^2+4*4.9*(h+R*sin(ang))))/9.8;
    %trayectoria
    x=@(t) R*cos(ang)-w*R*sin(ang)*t;
    y=@(t) R*sin(ang)+w*R*cos(ang)*t-4.9*t.^2;
    fplot(x,y,[0,T]);
end
axis equal
hold off
xlabel('x')
ylabel('y')
grid on
title('Tiro parabólico')

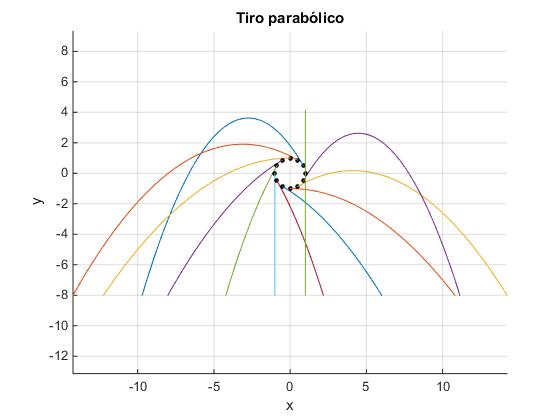
Alcance máximo

Si el suelo está a una distancia h por debajo el origen. El alcance de una gota que sale de la posición θ se calcula poniendo en las ecuaciones del movimiento y=-h.

$\begin{array}{l} x = R \cos θ - v_{0} \sin θ \cdot t \\ - h = R \sin θ + v_{0} \cos θ \cdot t - \frac{1}{2} g t^{2} \end{array}$

Dado el ángulo θ, calculamos el tiempo de vuelo t, en la segunda ecuación y lo sustituimos en la primera para calcular el alcance x.

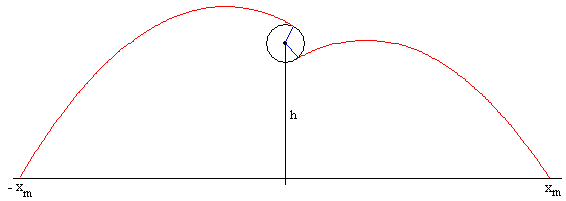
Ahora bien, nuestra tarea será determinar la posición inicial, o el ángulo θ_m, de la gota o gotas que llegan más lejos. Como vemos en la figura, hay dos ángulos para los cuales el alcance es máximo e igual a x_m.

El alcance x es una función del tiempo de vuelo t y del ángulo θ en la primera ecuación, y el tiempo de vuelo t es una función del ángulo θ, en la segunda ecuación. No parece a primera vista, una tarea sencilla, expresar x en función del ángulo θ, y despejar θ en la ecuación que nos da la condición de extremo dx/dθ=0. Realizaremos el cálculo de los ángulos θ_m siguiendo el procedimiento descrito en el artículo citado en las referencias.

Expresamos las ecuaciones del tiro parabólico en forma vectorial

$\vec{r} = \vec{r_{0}} + \vec{v_{0}} t + \frac{1}{2} \vec{g} t^{2}$

donde

$\begin{array}{l} \vec{r} = x \hat{i} + y \hat{j} \\ \vec{r_{0}} = R \cos θ \hat{i} + R \sin θ \hat{j} \\ \vec{v_{0}} = - v_{0} \sin θ \hat{i} + v_{0} \cos θ \hat{j} \\ \vec{g} = - g \hat{j} \end{array}$

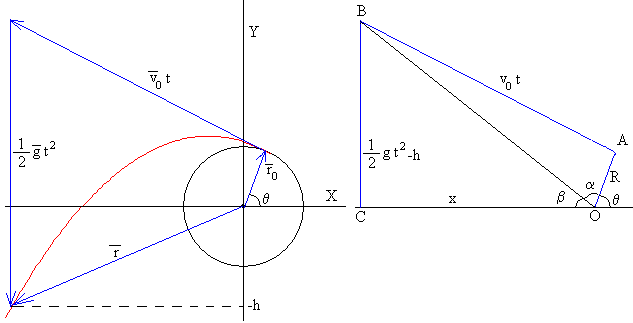
Dibujamos los tres vectores $\vec{r_{0}}, \vec{v_{0}} t, \frac{1}{2} \vec{g} t^{2}$ , y el vector suma $\vec{r}$ , tal como se muestra en la parte izquierda de la figura. En la parte derecha, observamos dos triángulos rectángulos OAB y OBC con la hipotenusa OB común, se cumplirá que

$R^{2} + {(v_{0} t)}^{2} = x^{2} + {(\frac{1}{2} g t^{2} - h)}^{2}$

De este modo, expresamos x solamente en función del tiempo t.

$x^{2} = - \frac{1}{4} g^{2} t^{4} + (v_{0}^{2} + g h) t^{2} + (R^{2} - h^{2})$

El extremo (máximo) de x se calcula derivando x con respecto a t.

$\frac{d x}{d t} = - g^{2} t^{3} + 2 (v_{0}^{2} + g h) t = 0 t_{m} = \frac{\sqrt{2 (v_{0}^{2} + g h)}}{g}$

El alcance x_m para el instante t_m es

$x_{m} = \pm \frac{\sqrt{v_{0}^{4} + 2 v_{0}^{2} g h + g^{2} R^{2}}}{g}$

Calculamos el ángulo θ_m de la gota cuyo punto de impacto es (-x_m, -h). Como vemos en la parte derecha de la figura θ_m=π-α-β.

$\begin{array}{l} θ_{m} = π - \arctan \frac{v_{o} t_{m}}{R} - \arctan \frac{\frac{1}{2} g t_{m}^{2} - h}{x_{m}} \\ θ_{m} = π - \arctan \frac{v_{o} \sqrt{2 (v_{0}^{2} + g h)}}{g R} - \arctan \frac{v_{0}^{2}}{\sqrt{v_{0}^{4} + 2 v_{0}^{2} g h + g^{2} R^{2}}} \end{array}$

Calculamos el ángulo θ_m de la gota cuyo punto de impacto es (x_m, -h).

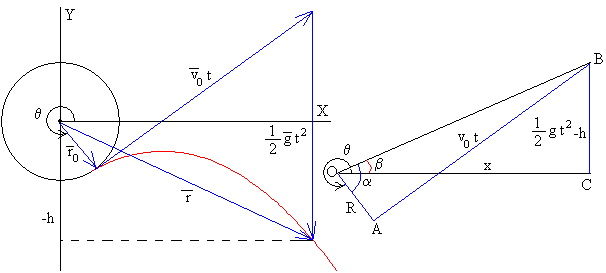
Como vemos en la parte derecha de la figura θ_m=2π-(α-β)=2π-α+β.

$θ_{m} = 2 π - \arctan \frac{v_{o} \sqrt{2 (v_{0}^{2} + g h)}}{g R} + \arctan \frac{v_{0}^{2}}{\sqrt{v_{0}^{4} + 2 v_{0}^{2} g h + g^{2} R^{2}}}$

Altura máxima

La gota que se lanza en la posición θ=0, se mueve verticalmente hacia arriba,

$\begin{array}{l} v_{y} = v_{0} - g t \\ y = v_{0} t - \frac{1}{2} g t^{2} \end{array}$

alcanzando una altura máxima y cuando v_y=0, cuyo valor es

$y = \frac{v_{0}^{2}}{2 g}$

Hay otras gotas que alcanzan una altura mayor, la que alcanza la altura máxima sale de la posición angular θ_m que vamos a calcular

La componente vertical de la velocidad de la gota que sale de la posición angular θ

$\begin{array}{l} v_{y} = v_{0} \cos θ - g t \\ y = R \sin θ + v_{0} \cos θ \cdot t - \frac{1}{2} g t^{2} \end{array}$

La máxima altura se alcanza cuando v_y=0, y su valor es

$y = R \sin θ + \frac{v_{0}^{2} \cos^{2} θ}{2 g}$

El ángulo θ, para el cual y es un extremo se obtiene dy/dθ=0

$\frac{d y}{d θ} = R \cos θ - \frac{v_{0}^{2}}{g} \sin θ \cdot \cos θ = 0$

Una solución es cosθ=0, con θ=π/2, que es cuando la gota sale horizontalmente. La solución buscada es

$θ_{m} = arcsin \frac{g R}{v_{0}^{2}}$

La altura máxima que alcanza la gota que parte de esta posición es

$y_{m} = \frac{g R^{2}}{2 v_{0}^{2}} + \frac{v_{0}^{2}}{2 g}$

y su abscisa es x_m=0, tal como vemos en la figura, más abajo

Ecuación de la envolvente.

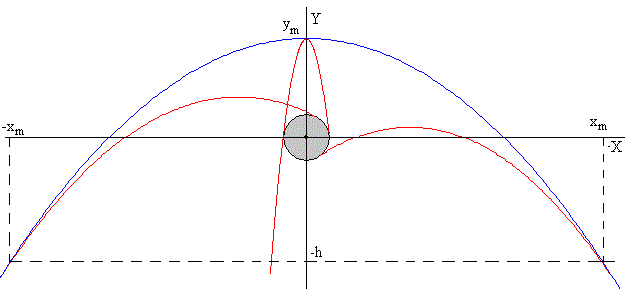
Como vemos en la figura, la envolvente (en color azul) es una parábola simétrica respecto del eje Y, su ecuación es y=ax²+b. Calculamos a y b sabiendo que la parábola pasa por el punto (0, y_m), y pasa por el punto (x_m, -h). Tenemos un sistema de dos ecuaciones con dos incógnitas

$\begin{array}{l} a x_{m}^{2} + b = - h \\ b = y_{m} \end{array}$

La ecuación de la envolvente, para el caso $v_{0}^{2} > g R$ , es la parábola

$y = \frac{g R^{2}}{2 v_{0}^{2}} + \frac{v_{0}^{2}}{2 g} - \frac{g x^{2}}{2 v_{0}^{2}}$

Ejemplo:

Sea ω=9.04 rad/s, y por tanto, v₀=9.04 m/s, y sea h=8 m la altura del eje del paraguas sobre el suelo

Consideremos la gota situada en la posición θ=60º

La posición de la gota en función del tiempo será

x=1.0·cos60º-9.04·sin60º·t
y=1.0·sin60º+ 9.04·cos60º·t-9.8·t²/2

Llega al suelo y=-8 m, en el instante t=1.88 s, y su distancia al origen será de x=-14.24 m.

Calculamos el alcance máximo

$x_{m} = \frac{\sqrt{{9.04}^{4} + 2 \cdot {9.04}^{2} \cdot 9.8 \cdot 8 + {9.8}^{2} {1.0}^{2}}}{9.8} = \pm 14.28 m$

El tiempo que tarda en llegar al suelo es

$t_{m} = \frac{\sqrt{2 ({9.04}^{2} + 9.8 \cdot 8)}}{9.8} = 1.83 s$

Las dos gotas que parten de las posiciones angulares

$\begin{array}{l} θ_{m} = 180 - \arctan \frac{9.04 \cdot 1.83}{1.0} - \arctan \frac{\frac{1}{2} 9.8 \cdot {1.83}^{2} - 8}{14.28} = 63.2 º \\ θ_{m} = 360 - \arctan \frac{9.04 \cdot 1.83}{1.0} + \arctan \frac{\frac{1}{2} 9.8 \cdot {1.83}^{2} - 8}{14.28} = 303.7 º \end{array}$

su alcance es máximo

La gota que parte de la posición angular

$θ_{m} = arcsin \frac{9.8 \cdot 1.0}{{9.04}^{2}} = 6.9 º$

alcanza la altura máxima y_m

$y_{m} = \frac{9.8 \cdot {1.0}^{2}}{2 \cdot {9.04}^{2}} + \frac{{9.04}^{2}}{2 \cdot 9.8} = 4.23 m$

Actividades

Se introduce

La velocidad angular de rotación ω, en rad/s, en el control titulado Velocidad angular.
El radio del paraguas se ha fijado en el programa interactivo en el valor R=1 m

Se pulsa el botón titulado Nuevo.

Se observa el movimiento de las gotas situadas en los extremos de las varillas del paraguas en las posiciones: 0º, 30º, 60º, 90º, 120º, 150º, 180º, 210º, 240º, 270, 300º, y 330º.

Conocida la altura h del paraguas sobre el suelo, el lector puede calcular los alcances y el tiempo de vuelo de las gotas situadas en algunas de estas posiciones y en especial la situadas en θ=90º y θ=270º.

Velocidad angular (rad/s)

Referencias

Martínez D. Queiro S. An elementary solution for a difficult motion problem. The Physics Teacher 41, December 2003, pp. 518-520