Se dispara un proyectil contra un blanco móvil
Un cañón dispara un proyectil con velocidad v, haciendo un ángulo θ con la horizontal. Un carro de combate situado a una distancia d del cañón, en el momento del disparo, se mueve con velocidad constante u hacia el cañón. Se tratará de determinar el ángulo (o los ángulos) de disparo que hacen que el proyectil impacte en el carro de combate.
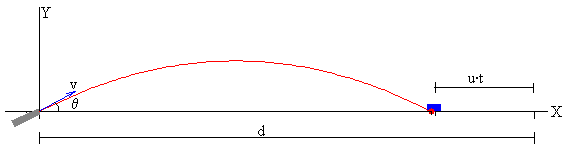
El proyectil se mueve bajo la aceleración constante de la gravedad, que es la composición de dos movimientos: Uniforme a lo largo del eje horizontal X y uniformemente acelerado a lo largo del eje vertical Y
El movimiento del carro de combate es rectilíneo y uniforme. Su posición x en función del tiempo es
x=d-u·t
El impacto del proyectil sobre el carro de combate se produce para y=0, es decir, en el instante t=2·v·sinθ/g
En dicho instante, han de coincidir las posiciones x de ambos móviles
Se pueden dar tres casos dependiendo de cual sean los datos y las incógnitas.
Se conoce la separación inicial d, el ángulo de tiro θ y la velocidad de disparo v. Calcular la velocidad u del carro de combate.
Se conoce la separación inicial d, el ángulo de tiro θ y la velocidad u del carro de combate. Calcular la velocidad de disparo v
El caso más interesante, es aquél en el que se conoce la separación inicial d, la velocidad de disparo v y la velocidad u del carro de combate, se pide calcular el ángulo (o ángulos) de tiro θ
Ángulos de disparo
Tenemos que hallar las raíces de la ecuación trascendente
v2·sin(2θ)+2u·v·sinθ-d·g=0
Existen varios procedimientos, el más simple, es trazar la gráfica de la función z=f(θ)
z=v2·sin(2θ)+2u·v·sinθ-d·g
y determinar aproximadamente, los puntos de corte de la función con el eje horizontal, tal como se aprecia en la figura.
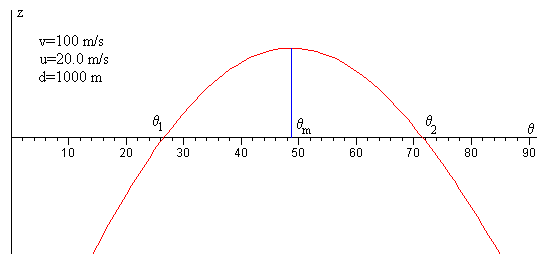
El máximo de la función z se produce
para un ángulo θm independiente de la distancia d
Los dos ángulos buscados θ1 y θ2 están en los intervalos (0, θm) y (θm, π/2) respectivamente.
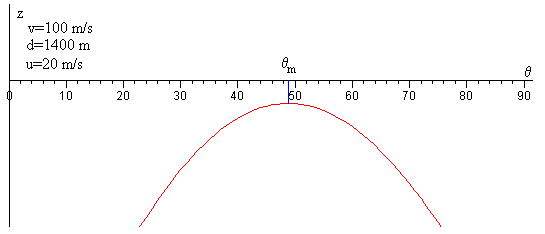
Existe una distancia dm para la cual la ecuación trascendente tiene una sola raíz θm. El máximo de la función f(θm) es z=0.
Si la distancia d entre el cañón y el carro de combate es mayor que dm, no hay ningún ángulo para el que se pueda producir impacto, la ecuación trascendente carece de raíces, tal como puede verse en la figura.
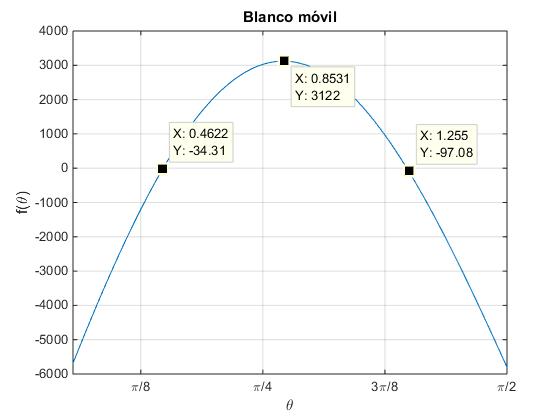
Ejemplo
Para una velocidad del carro de combate u=20.0 m/s, el máximo de la función f(θ) se produce para
Los ángulos de disparo que producen impacto en el carro de combate están comprendidos entre (0, 48.8º) y (48.8º, 90º) y son θ1=26.6º y θ2=71.5º, tal como puede verse en la primera representación gráfica
v=100; %velocidad de disparo
u=20; %velocidad del carro
d=1000; %distancia inicial entre el cañón y el carro
f= @(x) v^2*sin(2*x)+2*u*v*sin(x)-d*9.8;
fplot(f,[10,90]*pi/180)
set(gca,'XTick',0:pi/8:pi/2)
set(gca,'XTickLabel',{'0','\pi/8','\pi/4','3\pi/8','\pi/2'})
grid on
xlabel('\theta')
ylabel('f(\theta)')
title('Blanco móvil')
%ángulos de tiro
fzero(f,[0 0.85])*180/pi
fzero(f,[0.85 pi/2])*180/pi
ans = 26.6061 ans = 71.5446
Actividades
- La velocidad v de disparo del proyectil se ha fijado en 100 m/s.
- La distancia horizontal d entre el cañón y el carro de combate en el momento del disparo se ha fijado en 1000 m.
- El programa interactivo genera un número aleatorio comprendido entre 0 y 50 que representa la velocidad u del carro de combate.
- Se establece el ángulo de disparo, en el control titulado Angulo.
Se pulsa el botón titulado Nuevo
Observamos el movimiento del carro de combate desde la posición inicial x=1000 m, hacia el origen donde se encuentra el cañón.
- Se cambia el ángulo de tiro y se pulsa el botón titulado Nuevo
- Se ensaya con varios ángulos de disparo hasta dar en el blanco.
Referencias
Montalvo D. Solving an "unsolvable" projectile-motion problem. The Physics Teacher, Vol 37, April 1999, pp. 226-227

