Consideremos un condensador consistente en dos placas circulares de radio R separadas una distancia d, donde d<<R. Las placas del condensador se conectan a una batería cuya diferencia de potencial constante es V.

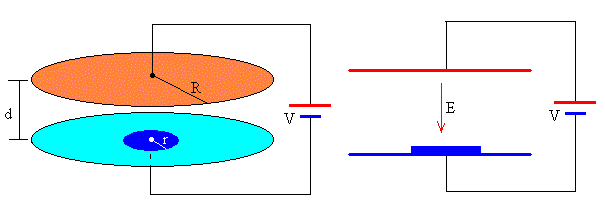
Un pequeño disco de masa m, de radio r<<R y de espesor w<<r  se coloca en el centro de la placa inferior, tal como se muestra en la figura.

Se supondrá que las placas y el disco son conductores perfectos y se despreciarán los efectos de los bordes.

Carga del disco

Las placas del condensador están cargadas con una carga Q, positiva (color rojo) en la placa superior y negativa (color azul) en la inferior. La densidad de carga es σ=Q/(πR²)

El campo eléctrico E es uniforme en el interior del condensador

${\displaystyle E=\frac{\sigma }{{\epsilon }_0}=\frac{Q}{\pi R^2{\epsilon }_0}=\frac{V}{d}}$

La carga Q de las placas del condensador es

${\displaystyle Q=\frac{V}{d}\pi R^2{\epsilon }_0}$

Suponiendo una distribución uniforme de la carga en la superficie de la placa, es decir, σ es constante, el pequeño disco situado en contacto con la placa inferior contiene una carga

${\displaystyle q=\sigma \pi r^2=\frac{\pi r^2}{\pi R^2}Q=\frac{V}{d}\pi r^2{\epsilon }_0}$

Movimiento del disco

Movimiento hacia arriba

Examinamos ahora el movimiento del disco hacia arriba, de la placa negativa a la positiva. Para ello, situamos el origen en la placa inferior y el eje Y apunta hacia arriba, de modo que la velocidad inicial y la aceleración son positivas.

El disco está cargado con una carga q negativa, el campo eléctrico ejerce una fuerza hacia arriba qE. Si esta fuerza es mayor que el peso mg, el disco asciende, en caso contrario, el disco permanece en reposo sobre la placa inferior del condensador.

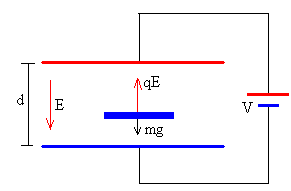
Si qE>mg la aceleración del disco es 

${\displaystyle a_{-}=\frac{qE}{m}-g=\frac{{(V/d)}^2{\epsilon }_0}{\rho w}-g}$

donde hemos supuesto que el disco es un pequeño cilindro de radio de la base r y altura w y está hecho de un material de densidad ρ, su masa es m=ρ(πr²)w.

Las ecuaciones del movimiento rectilíneo uniformemente acelerado para el movimiento ascendente son:

${\displaystyle v=v_{-0}+a_{-}ty=v_{-0}t+\frac{1}{2}{a}_{-}{t}^2}$

donde v_-0=0 es la velocidad inicial de partida.

El disco llega a la placa positiva y=d en el instante

${\displaystyle t_{-}=\frac{-v_{-0}+\sqrt{v_{-0}^2+2a_{-}d}}{a_{-}}}$

La velocidad con la que llega es

${\displaystyle v_{-}^2=v_{-0}^2+2a_{-}d}$

Balance energético

• Pondremos el nivel cero de energía potencial gravitatoria en la placa inferior, cuando un cuerpo se mueve hacia arriba, gana energía potencial.

• Cuando una carga positiva se mueve en el sentido del campo eléctrico, disminuye su energía potencial. Del mismo modo, cuando una carga negativa se mueve en sentido contrario al campo eléctrico, su energía potencial disminuye.

En la posición inicial de partida, la energía del disco es cinética y potencial eléctrica

${\displaystyle U_i=\frac{1}{2}m{v}_{-0}^2+qV}$

En la posición final, cuando llega a la placa positiva, su energía es potencial gravitatoria y cinética.

${\displaystyle U_f=\frac{1}{2}m{v}_{-}^2+mgd}$

Aplicamos el principio de conservación de la energía y obtenemos el mismo resultado que aplicando las ecuaciones de la dinámica.

${\displaystyle \begin{array}{l}{v}_{-}^2=v_{-0}^2+2\frac{qV}{m}-2gd=v_{-0}^2+2\left(\frac{V(V/d)\pi r^2{\epsilon }_0}{\rho \pi r^{2}w}-gd\right)=\\ v_{-0}^2+2\left(\frac{{(V/d)}^2{\epsilon }_0}{\rho w}-g\right)d=v_{-0}^2+2a_{-}d\end{array}}$

Choque del disco con la placa superior positiva

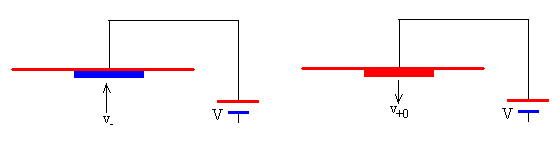
El disco con velocidad v_- choca con la placa, la velocidad del disco después del choque es

v₊₀=ev_-

siendo e≤1 el coeficiente de restitución. El valor e=1 corresponde al choque elástico

En el momento del choque, el disco pierde su carga q negativa y adquiere una carga igual y de sentido contrario, q positiva. La batería suministra carga a las placas a fin de mantener constante la carga Q de las mismas.

Movimiento hacia abajo

Examinamos el movimiento del disco hacia abajo, de la placa positiva a la negativa. Cambiamos el origen y el sentido del eje vertical. Situamos el origen en la placa superior y el eje Y apunta ahora, hacia abajo, de modo que la velocidad inicial y la aceleración son positivas. Ponemos el contador de tiempo t a cero.

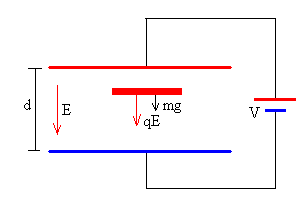
El disco está cargado con una carga q positiva, el campo eléctrico ejerce una fuerza hacia abajo qE. La aceleración del disco es

${\displaystyle a_{+}=\frac{qE}{m}+g=\frac{{(V/d)}^2{\epsilon }_0}{\rho w}+g}$

Las ecuaciones del movimiento rectilíneo uniformemente acelerado para el movimiento descendente son:

${\displaystyle v=v_{+0}+a_{+}ty=v_{+0}t+\frac{1}{2}{a}_{+}{t}^2}$

El disco llega a la placa negativa y=d en el instante

${\displaystyle t_{+}=\frac{-v_{+0}+\sqrt{v_{+0}^2+2a_{+}d}}{a_{+}}}$

La velocidad con la que llega es

${\displaystyle v_{+}^2=v_{+0}^2+2a_{+}d}$

Balance energético

• Cuando un cuerpo se mueve hacia abajo, su energía potencial gravitatoria disminuye.

• Cuando una carga positiva se mueve en el sentido del campo eléctrico, disminuye su energía potencial.

En la posición inicial de partida, la energía del disco es cinética, potencial eléctrica y gravitatoria.

${\displaystyle U_i=\frac{1}{2}m{v}_{+0}^2+qV+mgd}$

En la posición final, cuando llega a la placa positiva, su energía es cinética

${\displaystyle U_f=\frac{1}{2}m{v}_{+}^2}$

Aplicamos el principio de conservación de la energía y obtenemos el mismo resultado que aplicando las ecuaciones de la dinámica.

$$\begin{gathered} {\displaystyle v_{+}^2=v_{+0}^2+2\left(\frac{V(V/d)\pi r^2{\epsilon }_0}{\rho \pi r^{2}w}+gd\right)=v_{+0}^2+2\left(\frac{{(V/d)}^2{\epsilon }_0}{\rho w}+g\right)d \\ =v_{+0}^2+2a_{+}d} \end{gathered}$$

Choque del disco con la placa inferior negativa

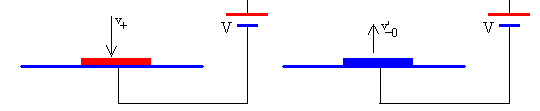
El disco con velocidad v₊ choca con la placa. La velocidad del disco después del choque es

v’_-0=ev₊

En el momento del choque el disco pierde su carga q positiva y adquiere una carga igual y de sentido contrario, q negativa. La batería tiene que suministrar carga a las placas a fin de mantener constante la carga Q de las mismas.

De este modo, hemos completado un ciclo, partiendo el disco de la placa inferior con una velocidad v’_-0

Oscilación completa

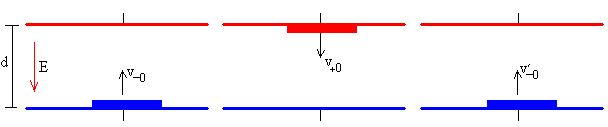
Resumimos las ecuaciones deducidas en el apartado anterior

El disco parte de la placa inferior con velocidad v_-0 y llega a la placa superior con velocidad

${\displaystyle v_{-}^2=v_{-0}^2+2a_{-}d{a}_{-}=\frac{qV}{md}-g}$

Choca con la placa superior

v₊₀=ev_-

El disco parte de la placa superior con velocidad v₊₀ y llega a la placa inferior con velocidad

${\displaystyle v_{+}^2=v_{+0}^2+2a_{+}d{a}_{+}=\frac{qV}{md}+g}$

Choca con la placa inferior y rebota con velocidad

v’_-0=ev₊

Vamos a relacionar las velocidades al comienzo de dos oscilaciones consecutivas, v’_-0 con v_-0

${\displaystyle \begin{array}{l}{v}_{+0}^2=e^2\left(v_{-0}^2+2a_{-}d\right)\\ v{\text{'}}_{-0}^2=e^2\left(e^2\left(v_{-0}^2+2a_{-}d\right)+2a_{+}d\right)=e^4{v}_{-0}^2+2e^4\left(\frac{qV}{m}-gd\right)+2e^2\left(\frac{qV}{m}+gd\right)\end{array}}$

El periodo P o tiempo que tarda en completar una oscilación vale

${\displaystyle P=t_{-}+t_{+}=\frac{-v_{-0}+\sqrt{v_{-0}^2+2a_{-}d}}{a_{-}}+\frac{-v_{+0}+\sqrt{v_{+0}^2+2a_{+}d}}{a_{+}}}$

Ejemplo:

Datos:

• Distancia entre las placas, d=0.1 m=10 cm

• Diferencia de potencial entre las placas V=250000 V

• Espesor del disco, w=0.002 m=2 mm

• Densidad del disco de aluminio, ρ=2700 kg/m³

• Coeficiente de restitución, e=0.9

Los valores de las aceleraciones son:

$$\begin{gathered} {\displaystyle \begin{array}{l}{a}_{-}=\frac{qV}{md}-g=\frac{(V/d)}{\rho \pi r^{2}w}\frac{\pi r^2{\epsilon }_{0}V}{d}-g=\frac{{\epsilon }_0}{\rho w}{\left(\frac{V}{d}\right)}^2-g= \\ \frac{{(250000/0.1)}^2}{2700·0.002·4\pi ·9·{10}^9}-9.8=0.4337{\text{m/s}}^{\text{2}}\\ a_{+}=\frac{qV}{md}+g=\frac{{\epsilon }_0}{\rho w}{\left(\frac{V}{d}\right)}^2+g=\frac{{(250000/0.1)}^2}{2700·0.002·4\pi ·9·{10}^9}+9.8=20.0337{\text{m/s}}^{\text{2}}\end{array}} \end{gathered}$$

La diferencia de potencial mínima que logra mover el disco hacia arriba se calcula poniendo a_-=0, y despejando V. Con los datos del ejemplo, V=244645 V

Calculamos las velocidades v_-0 al comienzo de cada oscilación y v₊₀ cuando retorna, sabiendo que la velocidad inicial v_-0=0.

${\displaystyle v_{+0}^2=e^2\left(v_{-0}^2+2a_{-}d\right)v{\text{'}}_{-0}^2=e^2\left(v_{+0}^2+2a_{+}d\right)}$

d=0.1; %distancia entre placas
V=250000; %diferencia de potencial entre las placas
w=0.002; %Espesor del disco
rho=2700; %Densidad del disco de aluminio
e=0.9; %Coeficiente de restitución

a_menos=(V/d)^2/(rho*w*4*pi*9e9)-9.8;
a_mas=(V/d)^2/(rho*w*4*pi*9e9)+9.8;
if a_menos<=0
    disp('El disco no asciende')
    return;
end

disp(['P(s)     ','      V_0 (m/s)'])
v0_2_menos=0;
for i=1:15
    v0_2_mas=e^2*(v0_2_menos+2*a_menos*d);
    P=(-sqrt(v0_2_menos)+sqrt(v0_2_menos+2*a_menos*d))/a_menos+
(-sqrt(v0_2_mas)+sqrt(v0_2_mas+2*a_mas*d))/a_mas;
    v0_2_menos=e^2*(v0_2_mas+2*a_mas*d);
    disp([P,sqrt(v0_2_menos)]);
end

  P(s)      V_0 (m/s)
    0.7666    1.8172
    0.1017    2.3386
    0.0823    2.6250
    0.0744    2.7970
    0.0704    2.9044
    0.0681    2.9727
    0.0667    3.0166
    0.0658    3.0452
    0.0652    3.0637
    0.0649    3.0758
    0.0647    3.0838
    0.0645    3.0890
    0.0644    3.0924
    0.0643    3.0946
    0.0643    3.0960

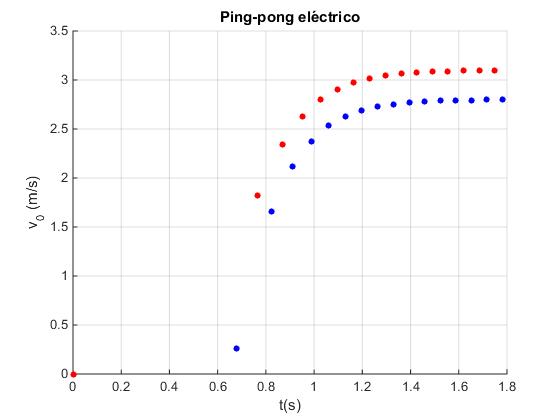
En la columna de la izquierda se proporciona los datos del periodo P de las oscilaciones del disco que va disminuyendo hasta que alcanza un valor constante. Sin embargo, la velocidad v_-0 va aumentado hasta que alcanza un valor constante, tal como se aprecia en la figura.

d=0.1; %distancia entre placas
V=250000; %diferencia de potencial entre las placas
w=0.002; %Espesor del disco
rho=2700; %Densidad del disco de aluminio
e=0.9; %Coeficiente de restitución

a_menos=(V/d)^2/(rho*w*4*pi*9e9)-9.8;
a_mas=(V/d)^2/(rho*w*4*pi*9e9)+9.8;
if a_menos<=0
    disp('El disco no asciende')
    return;
end
t=zeros(0,34);
v=zeros(0,34);
v0_2_menos=0;
t(1)=0;
v(1)=0;
for i=1:2:32
    t(i+1)=t(i)+(-sqrt(v0_2_menos)+sqrt(v0_2_menos+2*a_menos*d))/a_menos;
    v0_2_mas=e^2*(v0_2_menos+2*a_menos*d);
    v(i+1)=sqrt(v0_2_mas);
    t(i+2)=t(i+1)+(-sqrt(v0_2_mas)+sqrt(v0_2_mas+2*a_mas*d))/a_mas;
    v0_2_menos=e^2*(v0_2_mas+2*a_mas*d);
    v(i+2)=sqrt(v0_2_menos);
end
hold on
plot(t(1:2:end-1),v(1:2:end-1),'ro','markersize',4,'markerfacecolor','r')
plot(t(2:2:end),v(2:2:end),'bo','markersize',4,'markerfacecolor','b')
hold off
grid on
xlabel('t(s)')
ylabel('v_0 (m/s)')
title('Ping-pong eléctrico')

Estado estacionario

El disco va ganado energía suministrada por el campo eléctrico del condensador, es decir, por la batería. Si el choque fuese completamente elástico e=1, la energía del disco crecería 2qV en cada oscilación.

${\displaystyle \frac{1}{2}mv{\text{'}}_{-0}^2=\frac{1}{2}m{v}_{-0}^2+2qV}$

El choque inelástico proporciona el mecanismo de pérdida de energía, de modo que al cabo de un cierto tiempo t, teóricamente infinito, se alcanza el estado estacionario, el disco completa una oscilación con un periodo P aproximadamente constante.

Cuando nos aproximamos al estado estacionario v’_-0≈v_-0

${\displaystyle \begin{array}{l}v{\text{'}}_{-0}^2=e^2\left(e^2\left(v_{-0}^2+2a_{-}d\right)+2a_{+}d\right)\\ (1-e^4)v_{-0}^2=2e^4{a}_{-}d+2e^2{a}_{+}d\end{array}}$

Con los datos del ejemplo, en el estado estacionario, las velocidades son

v_-0=3.10 m/s
v₊₀=2.80 m/s
y el periodo, P=0.064 s

De otra forma

${\displaystyle \begin{array}{l}(1-e^4)v_{-0}^2=2e^4\left(\frac{qV}{m}-gd\right)+2e^2\left(\frac{qV}{m}+gd\right)\\ \frac{1}{2}m{v}_{-0}^2=\frac{e^2}{1-e^2}qV+\frac{e^2}{1+e^2}mgd\\ \frac{1}{2}m{v}_{+0}^2=\frac{e^2}{1-e^2}qV-\frac{e^2}{1+e^2}mgd\end{array}}$

En el estado estacionario v’_-0=v_-0, de modo

${\displaystyle v_{+0}^2=e^2\left(v_{-0}^2+2a_{-}d\right)v_{-0}^2=e^2\left(v_{+0}^2+2a_{+}d\right)}$

El periodo en el estado estacionario se escribe

${\displaystyle \begin{array}{l}P=t_{-}+t_{+}=\frac{-v_{-0}+\sqrt{v_{-0}^2+2a_{-}d}}{a_{-}}+\frac{-v_{+0}+\sqrt{v_{+0}^2+2a_{+}d}}{a_{+}}\\ =\frac{-v_{-0}+v_{0+}/e}{a_{-}}+\frac{-v_{0+}+v_{0-}/e}{a_{+}}\end{array}}$

Aparentemente, no hay una expresión sencilla para el periodo P en el estado estacionario en términos de V, m, d, g y e.

Intensidad de la corriente eléctrica es

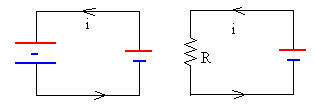
Durante el periodo P de una oscilación la batería trasporta una carga 2q a las placas. La intensidad es

${\displaystyle i=\frac{2q}{P}}$

La resistencia equivalente del circuito es

R=V/i

Aproximaciones

Cuando qV>>mgd

Las aceleraciones a_- y a₊ son prácticamente iguales

${\displaystyle a=a_{-}=a_{+}\approx \frac{qV}{md}}$

El disco parte de la placa inferior con velocidad v_-0

La velocidad con la que llega a la placa superior es

${\displaystyle v_{-}^2=v_{-0}^2+2ad}$

El disco con velocidad v_- choca con la placa, la velocidad del disco después del choque es

v₊₀=ev_-

La velocidad con la que llega a la placa inferior es

${\displaystyle v_{+}^2=v_{+0}^2+2ad}$

El disco con velocidad v₊ choca con la placa inferior, la velocidad del disco después del choque es

v’_-0=ev₊

Relacionamos las velocidades iniciales al comienzo de dos oscilaciones consecutivas v_-0 y v'_-0

${\displaystyle v{\text{'}}_{-0}^2=e^4{v}_{-0}^2+2(e^2+e^4)ad}$

En el estado estacionario v’_-0≈ v_-0

${\displaystyle \frac{1}{2}m{v}_{-0}^2=\frac{e^2}{1-e^2}qV}$

El tiempo que tarda en ascender o descender es

${\displaystyle t=\frac{-v_{-0}+\sqrt{v_{-0}^2+2ad}}{a}=\sqrt{\frac{1-e}{1+e}}\sqrt{\frac{2m{d}^2}{qV}}}$

La intensidad i de la corriente eléctrica es

${\displaystyle i=\frac{2q}{2t}=\sqrt{\frac{1+e}{1-e}}\sqrt{\frac{q^{3}V}{2m{d}^2}}=\sqrt{\frac{1+e}{1-e}}\sqrt{\frac{{({\epsilon }_0\pi r^2)}^3}{2m{d}^5}}{V}^2}$

La intensidad i es directamente proporcional al cuadrado de la diferencia de potencial V entre las placas del condensador

Actividades

Se introduce

• El coeficiente de restitución, e, en el control titulado Coef. restitución

• La diferencia de potencial entre las placas, V, en el control titulado d.d.p.

• La densidad ρ del material del que está hecho el disco, eligiendo uno en el control titulado Material.

El programa interactivo ha fijado los siguientes datos:

• El espesor del disco, w=2mm=0.002 m

• La distancia entre las placas, d=10 cm=0.1 m

Se pulsa el botón titulado Nuevo

Se observa, ascender el disco, si la diferencia de potencial entre las placas es superior al valor crítico, es decir, si la aceleración a_->0.

Después de varias oscilaciones, se alcanza el estado estacionario.

En la parte derecha, se representa la velocidad v_-0 con que inicia el disco su movimiento ascendente desde la placa inferior, en función del tiempo t.

Dicha velocidad tiende hacia el valor constante

${\displaystyle \frac{1}{2}m{v}_{-0}^2=\frac{e^2}{1-e^2}qV+\frac{e^2}{1+e^2}mgd}$

Cuando el coeficiente de restitución e es pequeño, prácticamente desde el primer choque, se alcanza el estado estacionario.

En el borde derecho, una barra de colores representa el balance energético, la suma de las tres clases de energía:

• La energía cinética, en color azul claro

• La energía potencial gravitatoria, en color amarillo

• La energía potencial eléctrica, en color rojo

La energía se conserva cuando el disco asciende o desciende y cambia, en el momento en el que el disco choca con las placas superior e inferior.

La energía del disco, va creciendo hasta que alcanza un valor límite en el estado estacionario. En la parte superior derecha, se proporciona el valor de la energía del disco por unidad de masa.

El radio del disco coincide con el radio de las placas del condensador

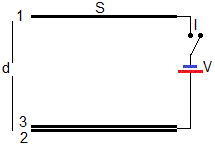
Un la situación anterior, hemos supuesto que el disco, que se mueve entre las placas del condensador, es pequeño y que no perturba el campo eléctrico existente entre dichas placas. En este apartado, vamos a analizar el movimiento de un disco que tiene las mismas dimensiones que la placas del condensador

Las dos placas del condensador plano-paralelo están separadas una distancia d, su área es S y están conectadas a una batería V. Un disco 3 de masa m y de las mismas dimensiones se coloca encima de la segunda placa. Se cierra el interruptor I y observaremos al disco 3 moviéndose entre las dos placas fijas.

Movimiento hacia arriba

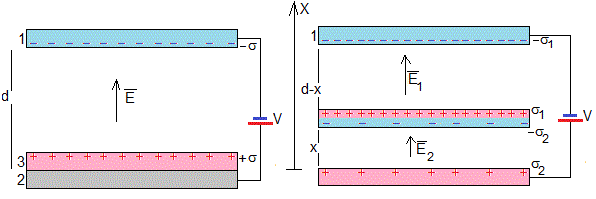
En el instante inicial, las cargas de la placas 1 y del disco 3, son

${\displaystyle E=\frac{V}{d}=\frac{\sigma }{{\epsilon }_0}}$

En el instante t, el disco 3 se eleva una altura x, por la conservación de la carga

${\displaystyle \sigma ={\sigma }_1-{\sigma }_2={\epsilon }_0\frac{V}{d}}$

Por otra parte, en la figura de la derecha

${\displaystyle V=E_{2}x+E_1\left(d-x\right)=\frac{{\sigma }_2}{{\epsilon }_0}x+\frac{{\sigma }_1}{{\epsilon }_0}\left(d-x\right)}$

Despejamos σ₁ y σ₂ en el sistema de dos ecuaciones, y calculamos los campos eléctricos E₁ y E₂

${\displaystyle E_1=\frac{V}{d}\left(1+\frac{x}{d}\right),E_2=\frac{V}{d}\frac{x}{d}}$

Las fuerzas sobre el disco 3 son

• El peso, mg

• La fuerza que ejercen los campos eléctricos sobre las cargas en el disco 3

${\displaystyle \begin{array}{l}F=\frac{1}{2}{\epsilon }_{0}S{E}_1^2-\frac{1}{2}{\epsilon }_{0}S{E}_2^2=\frac{1}{2}{\epsilon }_{0}S{\left(\frac{V}{d}\right)}^2\left({\left(1+\frac{x}{d}\right)}^2-\frac{x^2}{d^2}\right)\\ F=\frac{1}{2}{\epsilon }_{0}S{\left(\frac{V}{d}\right)}^2\left(1+2\frac{x}{d}\right)\end{array}}$

Se trata de una fuerza hacia arriba, contraria al peso

La aceleración del disco 3, es

${\displaystyle a=\frac{F-mg}{m}=\frac{{\epsilon }_{0}S{V}^2}{2m{d}^2}-g+\frac{{\epsilon }_{0}S{V}^2}{m{d}^3}x}$

Para que la placa se mueva hacia arriba

${\displaystyle \begin{array}{l}\frac{{\epsilon }_{0}S{V}^2}{2m{d}^2}>g\\ V_m=d\sqrt{\frac{2mg}{{\epsilon }_{0}S}}\end{array}}$

La fem V de la batería tiene que ser mayor que el mínimo V_m

La aceleración a es una función del desplazamiento x de la placa 3

${\displaystyle a=\frac{dv}{dt}=\frac{dv}{dx}\frac{dx}{dt}=v\frac{dv}{dx}}$

Integramos, con la condición inicial para x=0, v=v₀

${\displaystyle \begin{array}{l}v\frac{dv}{dx}=b+cx,\{\begin{array}{l}b=\frac{{\epsilon }_{0}S{V}^2}{2m{d}^2}-g>0\\ c=\frac{{\epsilon }_{0}S{V}^2}{m{d}^3}\end{array}\\ {\displaystyle \underset{v_0}{\overset{v}{\int }}v·dv}={\displaystyle \underset{0}{\overset{x}{\int }}\left(b+cx\right)dx}\\ \frac{1}{2}{v}^2-\frac{1}{2}{v}_0^2=bx+\frac{1}{2}c{x}^2\\ v=\sqrt{v_0^2+2bx+c{x}^2}\end{array}}$

Como v=dx/dt, integramos la ecuación diferencial con las condiciones iniciales, para t=0, x=0. El disco 3 emplea un tiempo t₁ en desplazarse d, distancia entre las placas

${\displaystyle \begin{array}{l}\frac{dx}{dt}=\sqrt{v_0^2+2bx+c{x}^2}\\ {\displaystyle \underset{0}{\overset{d}{\int }}\frac{dx}{\sqrt{v_0^2+2bx+c{x}^2}}={\displaystyle \underset{0}{\overset{t_1}{\int }}dt}}\end{array}}$

Para resolver la integral, se completan cuadrados

${\displaystyle {\displaystyle \int \frac{dx}{\sqrt{v_0^2+2bx+c{x}^2}}}=\frac{1}{\sqrt{c}}{\displaystyle \int \frac{dx}{\sqrt{\frac{v_0^2}{c}+2\frac{b}{c}x+x^2}}}=\frac{1}{\sqrt{c}}{\displaystyle \int \frac{dx}{\sqrt{{\left(x+\frac{b}{c}\right)}^2+\frac{v_0^2}{c}-\frac{b^2}{c^2}}}}}$

Hacemos el cambio de variable

${\displaystyle \begin{array}{l}t=x+\frac{b}{c},dt=dx\\ \frac{1}{\sqrt{c}}{\displaystyle \int \frac{dt}{\sqrt{t^2+a^2}}}=\frac{1}{\sqrt{c}}\text{arcsinh}\left(\frac{t}{a}\right)\text{=}\frac{1}{\sqrt{c}}\text{ln}\left(t+\sqrt{t^2+a^2}\right)\end{array}}$

Deshaciendo el cambio de variable

${\displaystyle {\displaystyle \int \frac{dx}{\sqrt{v_0^2+2bx+c{x}^2}}}=\frac{1}{\sqrt{c}}\text{ln}\left(x+\frac{b}{c}+\sqrt{{\left(x+\frac{b}{c}\right)}^2+\frac{v_0^2}{c}-\frac{b^2}{c^2}}\right)+C}$

El tiempo t₁ que emplea el disco 3 en chocar con la placa negativa 1, transfiriéndole la carga positiva σS, es

${\displaystyle t_1=\frac{1}{\sqrt{c}}\text{ln}\left(d+\frac{b}{c}+\sqrt{{\left(d+\frac{b}{c}\right)}^2+\frac{v_0^2}{c}-\frac{b^2}{c^2}}\right)-\frac{1}{\sqrt{c}}\text{ln}\left(\frac{b}{c}+\sqrt{\frac{v_0^2}{c}}\right)}$

Si el disco 3 parte del reposo, v₀=0

${\displaystyle \begin{array}{l}{t}_1=\frac{1}{\sqrt{c}}\text{ln}\left(\frac{cd+b}{b}+\frac{\sqrt{c}}{b}\sqrt{c{d}^2+2bd}\right)\\ t_1=\frac{d}{V}\sqrt{\frac{md}{{\epsilon }_{0}S}}\text{ln}\left(\frac{3{\epsilon }_{0}S{V}^2-2mg{d}^2+2\sqrt{2{\epsilon }_{0}S{V}^2}\sqrt{{\epsilon }_{0}S{V}^2-mg{d}^2}}{{\epsilon }_{0}S{V}^2-2mg{d}^2}\right)\end{array}}$

Movimiento hacia abajo

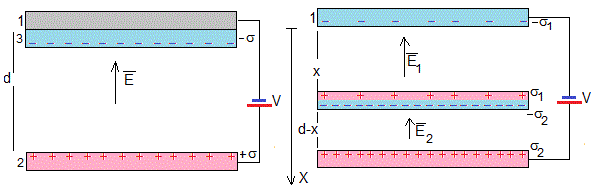
En el instante inicial, las cargas están en la superficie del disco 3 y de la placa 2, como se muestra en la figura de la izquierda

En el instante t el disco 3 se desplaza x. Por la conservación de la carga

${\displaystyle \sigma ={\sigma }_2-{\sigma }_1={\epsilon }_0\frac{V}{d}}$

Por otra parte, en la figura de la derecha

${\displaystyle V=E_{1}x+E_2\left(d-x\right)=\frac{{\sigma }_1}{{\epsilon }_0}x+\frac{{\sigma }_2}{{\epsilon }_0}\left(d-x\right)}$

Despejamos σ₁ y σ₂ en el sistema de dos ecuaciones, y calculamos los campos eléctricos E₁ y E₂

${\displaystyle E_2=\frac{V}{d}\left(1+\frac{x}{d}\right),E_1=\frac{V}{d}\frac{x}{d}}$

• El peso, mg

• La fuerza que ejercen los campos eléctricos sobre las cargas en el disco 3

${\displaystyle \begin{array}{l}F=\frac{1}{2}{\epsilon }_{0}S{E}_1^2-\frac{1}{2}{\epsilon }_{0}S{E}_2^2=\frac{1}{2}{\epsilon }_{0}S{\left(\frac{V}{d}\right)}^2\left(\frac{x^2}{d^2}-{\left(1+\frac{x}{d}\right)}^2\right)\\ F=-\frac{1}{2}{\epsilon }_{0}S{\left(\frac{V}{d}\right)}^2\left(1+2\frac{x}{d}\right)\end{array}}$

Se trata de una fuerza hacia abajo, del mismo sentido que el peso

Cambiamos la orientación del eje X, que ahora apunta hacia abajo. La aceleración del disco 3 (hacia abajo) es

${\displaystyle a=\frac{\left|F\right|+mg}{m}=\frac{{\epsilon }_{0}S{V}^2}{2m{d}^2}+g+\frac{{\epsilon }_{0}S{V}^2}{m{d}^3}x}$

El tiempo t₂ que tarda el disco 3 en chocar con la placa 2 y transferirle una carga σS negativa, es similar al de subida, solamente hay que cambiar -g por g

Haciendo que el radio r disco sea pequeño en comparación con el radio R de las placas del condensador, facilita la resolución de este interesante problema. Cuando el radio del disco es igual al de las placas del condensador entendemos mejor las distribución de cargas en el disco y la fuerza que ejercen los campos eléctricos entre las placas del condensador sobre dichas cargas

Referencias

Thoretical question 1: "Ping-Pong Resistor"

Strawson R., Lovett D. International Physics Olympiad Competition 2004 in South Korea. Physics Education. Vol 40 (2) March 2005, pp. 160-163

Chinese Physics Olympiad 2018 Finals. Theoretical Exam. Solution. Problem 2. https://physoly.tech/static/files/archive/CPhO-2018-F-S.pdf