Potencial constante

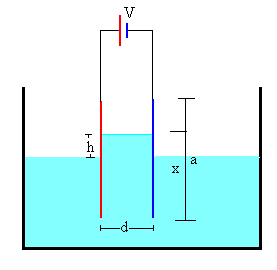
Consideremos un condensador plano-paralelo cuyas armaduras son perpendiculares a la superficie de un dieléctrico líquido de constante dieléctrica k. Cuando introducimos el condensador en el recipiente que contiene el dieléctrico su superficie libre se eleva entre las placas del condensador, tal como se muestra en la figura.

Sean a y b las dimensiones de la placa rectangular. Si el dieléctrico está introducido una longitud x en el condensador su capacidad es la suma de las capacidades de dos condensadores uno de longitud x con dieléctrico y otro de longitud a-x en el vacío.

${\displaystyle C=\frac{k\epsilon bx}{d}+\frac{{\epsilon }_{0}b(a-x)}{d}}$

Si la diferencia de potencial en el condensador V permanece constante, entonces la fuerza vertical que se ejerce sobre la superficie libre del líquido dieléctrico, perpendicularmente a las líneas del campo es

${\displaystyle F_x={\left(\frac{\partial U}{\partial x}\right)}_V=\frac{1}{2}{V}^2\frac{\partial C}{\partial x}=\frac{{\epsilon }_0(k-1)b}{2d}{V}^2}$

Esta es la fuerza que hace que el líquido ascienda

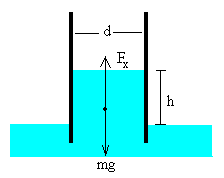
En el equilibrio la fuerza que ejerce el campo eléctrico sobre el dieléctrico F_x se iguala al peso de la columna de líquido mg=ρ·g·bhd.

${\displaystyle h=\frac{{\epsilon }_0(k-1)}{2\rho g}{\left(\frac{V}{d}\right)}^2}$

La presión p que hace la columna de líquido de altura h es

${\displaystyle p=\frac{F_x}{bd}=\frac{{\epsilon }_0(k-1)}{2d^2}{V}^2=\frac{1}{2}{\epsilon }_0(k-1)E^2}$

Donde E=V/d es la intensidad del campo eléctrico entre las placas del condensador vacío.

La presión, en la superficie de separación entre dos medios dieléctricos es proporcional al cuadrado de la intensidad del campo eléctrico E.

Balance energético

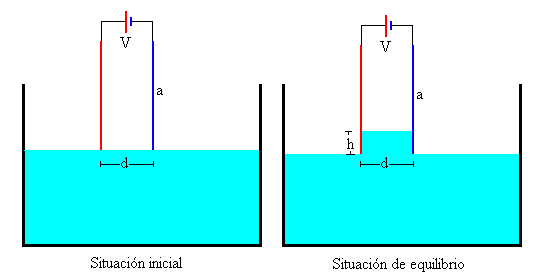
La capacidad del condensador con dieléctrico aumenta, para que la diferencia de potencial entre las placas se mantenga constante en V, la batería tiene que suministrar carga al condensador. La batería suministra energía para incrementar la energía electrostática del condensador y a la vez, elevar el centro de masas del líquido dieléctrico en h/2.

En la situación inicial la energía asociada al campo eléctrico del condensador vacío es

${\displaystyle C_0=\frac{{\epsilon }_{0}ab}{d}{U}_0=\frac{1}{2}{C}_0{V}^2}$

En la situación de equilibrio, el condensador tiene en su interior una porción h de dieléctrico líquido. La energía asociada al campo eléctrico del condensador es

${\displaystyle \begin{array}{l}C=\frac{k\epsilon bh}{d}+\frac{{\epsilon }_{0}b(a-h)}{d}{U}_{\epsilon }=\frac{1}{2}C{V}^2\\ U_{\epsilon }=\frac{1}{2}\frac{{\epsilon }_0(k-1)b}{d}h{V}^2+\frac{1}{2}\frac{{\epsilon }_{0}ab}{d}{V}^2=\frac{1}{4}\frac{{\epsilon }_0^2{(k-1)}^{2}b}{\rho g{d}^3}{V}^4+\frac{1}{2}\frac{{\epsilon }_{0}ab}{d}{V}^2=\frac{1}{4}\frac{{\epsilon }_0^2{(k-1)}^{2}b}{\rho g{d}^3}{V}^4+U_0\end{array}}$

La porción h de dieléctrico que ha ascendido ha adquirido una energía potencial gravitatoria, su centro de masas se encuentra a h/2 de altura.

${\displaystyle U_g=\rho (bdh)g\frac{h}{2}=\frac{1}{2}\rho gbd{h}^2=\frac{1}{2}\rho gbd\frac{{\epsilon }_0^2{(k-1)}^2}{4{\rho }^2{g}^2}{\left(\frac{V}{d}\right)}^4=\frac{1}{8}\frac{{\epsilon }_0^2{(k-1)}^{2}b}{\rho g{d}^3}{V}^4}$

La energía suministrada por la batería será la diferencia entre la energía final U_g+U_ε y la energía inicial U₀.

${\displaystyle W=U_g+U_{\epsilon }-U_0=\frac{3}{8}\frac{{\epsilon }_0^2{(k-1)}^{2}bd}{\rho g}{\left(\frac{V}{d}\right)}^4}$

Actividades

El programa interactivo genera un valor aleatorio de la constante dieléctrica k entre 300 y 400, cada vez que se pulsa el botón titulado Nuevo.

• La distancia d entre las placas está fijada en el programa y su valor es 0.2 mm.
• La densidad ρ del fluido está también fijado en el programa y su valor es de 1.02 g/cm³.

Se introduce un valor de la diferencia de potencial V entre las placas del condensador, en el control titulado d. d. potencial.

Ejemplo:

Leemos en el voltímetro una diferencia de potencial de 80 V y medimos la altura que se eleva el fluido dieléctrico en la regla graduada, h=25.97 mm.

${\displaystyle 25.97·{10}^{-3}=\frac{1}{4\pi ·9·{10}^9}\frac{k-1}{2·9.8·1.02·{10}^3}{\left(\frac{80}{2·{10}^{-4}}\right)}^{2}k=368}$

Carga constante

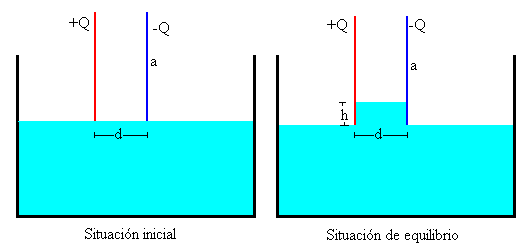
Un condensador de placas paralelas está fijado en posición vertical, su parte inferior está en contacto con un dieléctrico líquido. Determinar la altura h del líquido entre las placas, despreciando los efectos capilares, suponiendo que la distancia d entre las placas es mucho menor que las dimensiones lineales de las mismas.

La energía inicial del condensador cargado es

${\displaystyle U_0=\frac{1}{2}\frac{Q^2}{C_0}{C}_0=\frac{{\epsilon }_{0}ab}{d}}$

donde a (vertical) y b (horizontal) son las dimensiones de las placas rectangulares cargadas con una carga Q.

Cuando las placas entran en contacto con el dieléctrico líquido se ejerce una fuerza vertical sobre el mismo. La carga Q permanece constante. La disminución de la energía electrostática se compensa con el incremento de la energía potencial gravitatoria ya que no hay energía transferida al sistema desde el exterior.

Calculamos la capacidad C del condensador con una porción h de dieléctrico y su energía U_ε.

${\displaystyle \begin{array}{l}C=\frac{\epsilon kbh}{d}+\frac{{\epsilon }_{0}b(a-h)}{d}\\ U_{\epsilon }=\frac{1}{2}\frac{Q^2}{C}\end{array}}$

La energía potencial gravitatoria de la porción de fluido es

${\displaystyle U_g=\rho \left(bdh\right)g\frac{h}{2}=\frac{1}{2}\rho bdg{h}^2}$

Aplicamos el principio de conservación de la energía

U₀= U_ε+U_g

${\displaystyle h^2+\frac{a}{(k-1)}h-\frac{Q^2}{\rho g({\epsilon }_{0}a{b}^2)}=0}$

El campo eléctrico del condensador vacío es

${\displaystyle E_0=\frac{\sigma }{{\epsilon }_0}=\frac{Q}{{\epsilon }_{0}ab}}$

donde σ es la densidad de carga de cada una de las placas en C/m².

${\displaystyle \begin{array}{l}{h}^2+\frac{a}{(k-1)}h-\frac{{\epsilon }_0{E}_0^{2}a}{\rho g}=0\\ h=\frac{1}{2}\frac{a}{(k-1)}\left(-1+\sqrt{1+\frac{4{\epsilon }_0{E}_0^2{(k-1)}^2}{\rho ga}}\right)\end{array}}$

Habitualmente, la altura h de dieléctrico en el condensador es mucho menor que la altura a de las placas.

${\displaystyle h\approx \frac{{\epsilon }_0(k-1)}{\rho g}{E}_0^2}$

Movimiento del líquido dieléctrico

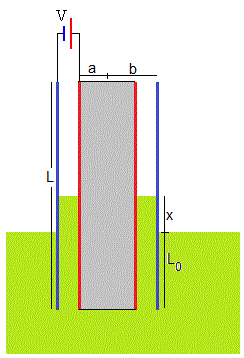
Consideremos un condensador cilíndrico de longitud L cuyo radio interior es a y exterior b, con L>>b

El condensador en posición vertical se introduce parcialmente en un líquido dieléctrico contenido en un recipiente grande, de tal manera, que la superficie del líquido esté lejos de los extremos del condensador. Siendo L₀ la parte sumergida

Se aplica un diferencia de potencial entre las placas del condensador, se observa que el líquido dieléctrico se eleva entre sus placas. En este apartado, calculamos la altura máxima que alcanza el líquido dieléctrico y el tiempo que tarda en alcanzarlo.

En el instante t=0, se concetan las placas del condensador a una batería, en el instante t el líquido se ha elevado x tal como se muestra en la figura

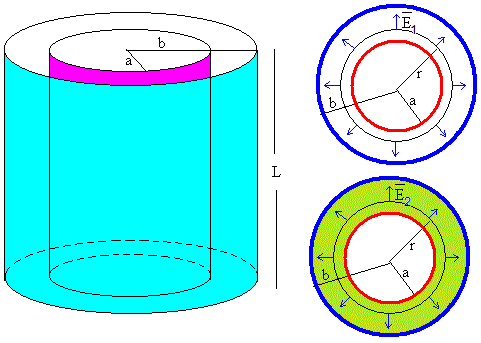
El campo eléctrico en el condensador cilíndrico tiene dirección radial y su módulo es (de acuerdo con la ley de Gauss)

${\displaystyle \begin{array}{l}{E}_1=\frac{{\lambda }_1}{2\pi {\epsilon }_{0}r}\\ E_2=\frac{{\lambda }_2}{2\pi \epsilon r}\end{array}}$

Donde ε₀ es la permitividad en el vacío y ε es la permitividad en el dieléctrico. λ₁ y λ₂ son las densidades lineales de carga libre de la parte superior (vacío) e inferior (dieléctrico)

La diferencia de potencial entre las placas es V

${\displaystyle \begin{array}{l}V={\displaystyle \underset{a}{\overset{b}{\int }}{E}_{1}dr=\frac{{\lambda }_1}{2\pi {\epsilon }_0}}\ln \frac{b}{a}\\ V={\displaystyle \underset{a}{\overset{b}{\int }}{E}_{2}dr=\frac{{\lambda }_2}{2\pi \epsilon }}\ln \frac{b}{a}\end{array}}$

La carga del condensador es

${\displaystyle \begin{array}{l}Q={\lambda }_1\left(L-(L_0+x)\right)+{\lambda }_2\left(L_0+x\right)=\frac{2\pi {\epsilon }_{0}V}{\ln \frac{b}{a}}\left(L-(L_0+x)\right)+\frac{2\pi \epsilon V}{\ln \frac{b}{a}}\left(L_0+x\right)=\\ \frac{2\pi {\epsilon }_{0}V}{\ln \frac{b}{a}}\left(L-(L_0+x)+\frac{\epsilon }{{\epsilon }_0}\left(L_0+x\right)\right)=\frac{2\pi {\epsilon }_{0}V}{\ln \frac{b}{a}}\left(L+\left(k-1\right)(L_0+x)\right),k=\frac{\epsilon }{{\epsilon }_0}\end{array}}$

La capacidad del condensador es

${\displaystyle C=\frac{Q}{V}=\frac{2\pi {\epsilon }_0}{\ln \frac{b}{a}}\left(L+\left(k-1\right)(L_0+x)\right)}$

Alternativamente, obtenemos la capacidad del condensador sumando de las capacidades de un condensador cilíndrico vacío de longitud L-(L₀+x) y de otro con dieléctrico de longitud L₀+x

${\displaystyle C=\frac{2\pi {\epsilon }_0\left(L-(L_0+x)\right)}{\ln \frac{b}{a}}+\frac{2\pi \epsilon \left(L_0+x\right)}{\ln \frac{b}{a}}=\frac{2\pi {\epsilon }_0}{\ln \frac{b}{a}}\left(L+\left(k-1\right)\left(L_0+x\right)\right)}$

Potencial constante

La energía del condensador es

${\displaystyle U=\frac{1}{2}C{V}^2}$

La fuerza sobre el dieléctrico es

${\displaystyle F={\left(\frac{dU}{dx}\right)}_V=\frac{\pi {\epsilon }_0}{\ln \frac{b}{a}}\left(k-1\right)V^2}$

Esta fuerza es constante

Ecuación del movimiento del líquido dieléctrico

Se trata de un problema de masa variable

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(m\frac{dx}{dt}\right)=F+\rho g{L}_0\pi \left(b^2-a^2\right)-mg\\ m=\rho \pi \left(b^2-a^2\right)\left(L_0+x\right)\end{array}}$

La segunda fuerza se justifica del siguiente modo: la presión en la parte inferior de la columna de líquido que hay dentro del condensador es mayor que la presión en la superficie libre, la diferencia es ρgL₀, donde ρ es la densidad del líquido dieléctrico. Esto da lugar a una fuerza hacia arriba producto de la diferencia de presión por el área de la sección, $\rho g{L}_0\pi \left(b^2-a^2\right)$, se le añade a la fuera electrostática F y al peso mg

Obtenemos una ecuación diferencial en términos de la variable x

${\displaystyle \left(L_0+x\right)\frac{d^{2}x}{d{t}^2}+{\left(\frac{dx}{dt}\right)}^2=\frac{{\epsilon }_0\left(k-1\right)V^2}{\rho \left(b^2-a^2\right)\ln \frac{b}{a}}+g{L}_0-\left(L_0+x\right)g}$

Para simplificar la ecuación diferencial, definimos las siguientes magnitudes

${\displaystyle \begin{array}{l}{a}_0=\frac{{\epsilon }_0\left(k-1\right)V^2}{\rho g\left(b^2-a^2\right)\ln \frac{b}{a}}=g{t}_0^2\\ \xi =\frac{L_0+x}{a_0},\tau =\frac{t}{t_0},\alpha =\frac{L_0}{a_0}\end{array}}$

Obtenemos la ecuación diferencial

${\displaystyle \begin{array}{l}{a}_0\xi \frac{a_0}{t_0^2}\frac{d^2\xi }{d{\tau }^2}+\frac{a_0^2}{t_0^2}{\left(\frac{d\xi }{d\tau }\right)}^2=a_{0}g+g\alpha a_0-\xi a_{0}g\\ \frac{a_0}{t_0^2}\xi \frac{d^2\xi }{d{\tau }^2}+\frac{a_0}{t_0^2}{\left(\frac{d\xi }{d\tau }\right)}^2=g+g\alpha -\xi g\\ a_0\xi \frac{d^2\xi }{d{\tau }^2}+a_0{\left(\frac{d\xi }{d\tau }\right)}^2=g{t}_0^2+g{t}_0^2\alpha -\xi g{t}_0^2\\ \xi \frac{d^2\xi }{d{\tau }^2}+{\left(\frac{d\xi }{d\tau }\right)}^2=1+\alpha -\xi \end{array}}$

Para resolver la ecuación diferencial se hace el cambio de variable

${\displaystyle \begin{array}{l}p=\frac{d\xi }{d\tau }\\ \frac{d^2\xi }{d{\tau }^2}=\frac{dp}{d\tau }=\frac{dp}{d\xi }\frac{d\xi }{d\tau }=p\frac{dp}{d\xi }\end{array}}$

La ecuación diferencial se convierte en

${\displaystyle \begin{array}{l}\xi p\frac{dp}{d\xi }+p^2=1+\alpha -\xi \\ \xi pdp+\left(p^2-1-\alpha +\xi \right)d\xi =0\end{array}}$

El procedimiento para obtener la solución de esta ecuación diferencial se explica en la página titulada Ecuaciones diferenciales (I) en el apartado Ecuaciones diferenciales exactas

Cambiamos el nombre de las variables p por t y ξ por x

${\displaystyle \begin{array}{l}\xi pdp+\left(p^2-1-\alpha +\xi \right)d\xi =0\\ \left(xt\right)dt+\left(t^2-1-\alpha +x\right)dx=0\\ P\left(t,x\right)dt+Q\left(t,x\right)dx=\mathrm{0,}\{\begin{array}{l}P\left(t,x\right)=xt\\ Q\left(t,x\right)=t^2-1-\alpha +x\end{array}\end{array}}$

Comprobamos que no es diferencial exacta

${\displaystyle \begin{array}{l}\frac{\partial P}{\partial x}=\frac{\partial Q}{\partial t}\\ t\ne 2t\end{array}}$

Buscamos un factor integrante μ

${\displaystyle \begin{array}{l}\frac{1}{P}\left(\frac{\partial Q}{\partial t}-\frac{\partial P}{\partial x}\right)=g(x),\mu =\exp \left({\displaystyle \int g(x)dx}\right)\\ \frac{1}{xt}\left(2t-2\right)=\frac{1}{x},\mu =\exp \left({\displaystyle \int \frac{1}{x}dx}\right)=\exp \left(\ln x\right)=x\end{array}}$

Comprobamos que es diferencial exacta

${\displaystyle \begin{array}{l}\frac{\partial \left(\mu P\right)}{\partial x}=\frac{\partial \left(\mu Q\right)}{\partial t}\\ \frac{\partial \left(x^{2}t\right)}{\partial x}=\frac{\partial \left(x\left(t^2-1-\alpha +x\right)\right)}{\partial t}\\ 2xt=2xt\end{array}}$

Obtenemos la solución de la ecuación diferencial

${\displaystyle \begin{array}{l}U={\displaystyle \int \mu P(t,x)dt+\phi (x)=}{\displaystyle \int x·xt·dt+\phi (x)=}{x}^2\frac{t^2}{2}+\phi (x)\\ \mu Q(t,x)=\frac{\partial U}{\partial x}\\ x\left(t^2-1-\alpha +x\right)=x{t}^2+\frac{\partial \phi }{\partial x}\\ \frac{\partial \phi }{\partial x}=x^2-\left(1+\alpha \right)x\\ \phi (x)={\displaystyle \int \left(x^2-\left(1+\alpha \right)x\right)dx}=\frac{x^3}{3}-\frac{1+\alpha }{2}{x}^2+C\\ U(x,t)=x^2\frac{t^2}{2}+\frac{x^3}{3}-\frac{1+\alpha }{2}{x}^2+C\end{array}}$

Regresando a la notación original, cambiando p por t, x por ξ

${\displaystyle \frac{1}{2}{\xi }^2{p}^2+\frac{{\xi }^3}{3}-\frac{1+\alpha }{2}{\xi }^2+C=0}$

La constante C se determina a partir de las condiciones iniciales, en el instante t=0, x=0, dx/dt=0. O bien, τ=0, ξ=L₀/a₀=α, p=dξ/dτ=0

${\displaystyle \begin{array}{l}\frac{{\alpha }^3}{3}-\frac{1+\alpha }{2}{\alpha }^2+C=0\\ C=\frac{1+\alpha }{2}{\alpha }^2-\frac{{\alpha }^3}{3}\end{array}}$

La ecuación que hay que integrar es

${\displaystyle \begin{array}{l}\frac{1}{2}{\xi }^2{\left(\frac{d\xi }{d\tau }\right)}^2=\frac{1}{3}\left({\alpha }^3-{\xi }^3\right)+\frac{1+\alpha }{2}\left({\xi }^2-{\alpha }^2\right)\\ \tau =\frac{1}{\sqrt{2}}{\displaystyle \underset{\alpha }{\overset{\xi }{\int }}\frac{\xi d\xi }{\sqrt{\frac{1+\alpha }{2}\left({\xi }^2-{\alpha }^2\right)-\frac{1}{3}\left({\xi }^3-{\alpha }^3\right)}}}\end{array}}$

El líquido dieléctrico alcanza la máxima altura cuando la velocidad es nula, p=dξ/dτ=0

${\displaystyle \begin{array}{l}\frac{1}{3}\left({\xi }^3-{\alpha }^3\right)=\frac{1+\alpha }{2}\left({\xi }^2-{\alpha }^2\right)\\ \frac{1}{3}\left(\xi -\alpha \right)\left({\xi }^2+\xi \alpha +{\alpha }^2\right)=\frac{1+\alpha }{2}\left(\xi -\alpha \right)\left(\xi +\alpha \right)\end{array}}$

Una solución es ξ=α, que es la altura inicial, las otras dos son

${\displaystyle \begin{array}{l}\frac{1}{3}\left({\xi }^3-{\alpha }^3\right)=\frac{1+\alpha }{2}\left({\xi }^2-{\alpha }^2\right)\\ \frac{1}{3}\left(\xi -\alpha \right)\left({\xi }^2+\xi \alpha +{\alpha }^2\right)=\frac{1+\alpha }{2}\left(\xi -\alpha \right)\left(\xi +\alpha \right)\\ \frac{1}{3}\left({\xi }^2+\xi \alpha +{\alpha }^2\right)=\frac{1+\alpha }{2}\left(\xi +\alpha \right)\\ \frac{1}{3}{\xi }^2-\frac{1}{2}\left(1+\frac{\alpha }{3}\right)\xi -\frac{1}{2}\alpha \left(1+\frac{\alpha }{3}\right)=0\\ {\xi }_m=\frac{1}{4}\left(\alpha +3+3\sqrt{{\alpha }^2+\frac{10}{3}\alpha +1}\right)\\ {\xi }_1=\frac{1}{4}\left(\alpha +3-3\sqrt{{\alpha }^2+\frac{10}{3}\alpha +1}\right)=-\frac{1}{4}\left(3\sqrt{{\alpha }^2+\frac{10}{3}\alpha +1}-\alpha -3\right)\end{array}}$

El tiempo Τ que tarda en alcanzar la altura máxima ξ_m es

${\displaystyle {\rm T}=\frac{1}{\sqrt{2}}{t}_0{\displaystyle \underset{\alpha }{\overset{{\xi }_m}{\int }}\frac{\xi d\xi }{\sqrt{-\frac{1}{3}\left(\xi -\alpha \right)\left(\xi -{\xi }_m\right)\left(\xi -{\xi }_1\right)}}}=\sqrt{\frac{3}{2}}{t}_0{\displaystyle \underset{\alpha }{\overset{{\xi }_m}{\int }}\frac{\xi d\xi }{\sqrt{\left(\xi -\alpha \right)\left({\xi }_m-\xi \right)\left(\xi -{\xi }_1\right)}}}}$

Buscamos en la tabla de integrales la solución

${\displaystyle \begin{array}{l}{\displaystyle \underset{u}{\overset{a}{\int }}\frac{xdx}{\sqrt{(a-x)(x-b)(x-c)}}}=\frac{2}{\sqrt{a-c}}F\left(\lambda ,p\right)+2\frac{a}{b}\sqrt{a-c}E\left(\lambda ,p\right),a>u\ge b>c\\ p=\sqrt{\frac{a-b}{a-c}},\lambda =\arcsin \left(\sqrt{\frac{a-u}{a-b}}\right)\end{array}}$

En este caso, a es ξ_m, u es b=α y c es ξ₁

${\displaystyle \begin{array}{l}\lambda =\arcsin (1)=\frac{\pi }{2}\\ E\left(\frac{\pi }{2},p\right)=E\left(p\right)\\ F\left(\frac{\pi }{2},p\right)=K\left(p\right)\\ p=\sqrt{\frac{a-b}{a-c}}=\sqrt{\frac{{\xi }_m-\alpha }{{\xi }_m+\left|{\xi }_1\right|}}\\ {\rm T}=\sqrt{6}{t}_0\left(\frac{1}{\sqrt{{\xi }_m+\left|{\xi }_1\right|}}K\left(p\right)+\frac{{\xi }_m}{\alpha }\sqrt{{\xi }_m+\left|{\xi }_1\right|}E\left(p\right)\right)\end{array}}$

E(p) y K(p) son integrales elípticas completas

Nota: la expresión del tiempo Τ difiere de la deducida por los autores del primer artículo citado en las Referencias

Datos

• radio interior, a=1.0 cm
• radio exterior, b=2.0 cm
• longitud del condensador, L=20 cm
• el extremos inferior está a una profundidad, L₀=10 cm
• Se conecta el condensador a una batería, V=5000 V

a=1/100; %radio interior
b=2/100; %radio exterior
L=20/100; %longitud del condensador
L0=10/100; %profundidad
V=5000; %batería
k=80; %permitividad relativa del líquido
rho=1000; %densidad del líquido

a0=(k-1)*V^2/(4*pi*9e9*rho*9.8*(b^2-a^2)*log(b/a));
alfa=L0/a0;
t0=sqrt(a0/9.8);
xi_m=(alfa+3+3*sqrt(alfa^2+10*alfa/3+1))/4;
xi_1=abs((3*sqrt(alfa^2+10*alfa/3+1)-alfa-3)/4); %valor absoluto
p2=(xi_m-alfa)/(xi_m+xi_1);
[K,E]=ellipke(p2);
T=sqrt(6)*t0*(K/sqrt(xi_m+xi_1)+xi_m*E*sqrt(xi_m+xi_1)/alfa);
disp([xi_m,a0*xi_m-L0]) %altura máxima
disp([T,t0*T]) %tiempo en alcanzarla

La altura máxima es ξ_m=13.6195 o bien, x_m=0.0167 m=1.67 cm. El tiempo que tarda en alcanzar la altura máxima es Τ=0.6038 o bien, t_m=0.0179 s

  13.6195    0.0167
   0.6038    0.0179

Carga constante

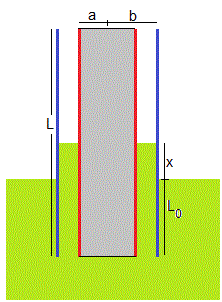
La fuerza sobre el dieléctrico es

${\displaystyle F=-{\left(\frac{dU}{dx}\right)}_Q=\frac{Q^2}{4\pi {\epsilon }_0}\frac{\left(k-1\right)\ln \frac{b}{a}}{{\left(L+\left(k-1\right)\left(L_0+x\right)\right)}^2}}$

Que es una fuerza variable

Ecuación del movimiento del líquido dieléctrico

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(m\frac{dx}{dt}\right)=\frac{Q^2}{4\pi {\epsilon }_0}\frac{\left(k-1\right)\ln \frac{b}{a}}{{\left(L+\left(k-1\right)\left(L_0+x\right)\right)}^2}+\rho g{L}_0\pi \left(b^2-a^2\right)-mg\\ m=\rho \pi \left(b^2-a^2\right)\left(L_0+x\right)\end{array}}$

Reordenando términos

${\displaystyle \begin{array}{l}\rho \pi \left(b^2-a^2\right){\left(\frac{dx}{dt}\right)}^2+\rho \pi \left(b^2-a^2\right)\left(L_0+x\right)\frac{d^{2}x}{d{t}^2}=\frac{Q^2}{4\pi {\epsilon }_0}\frac{\left(k-1\right)\ln \frac{b}{a}}{{\left(L+\left(k-1\right)\left(L_0+x\right)\right)}^2}+\rho g{L}_0\pi \left(b^2-a^2\right)-\rho \pi \left(b^2-a^2\right)\left(L_0+x\right)g\\ \left(L_0+x\right)\frac{d^{2}x}{d{t}^2}+{\left(\frac{dx}{dt}\right)}^2=\frac{Q^2}{4\pi {\epsilon }_0}\frac{\left(k-1\right)\ln \frac{b}{a}}{{\left(L+\left(k-1\right)\left(L_0+x\right)\right)}^2\rho \pi \left(b^2-a^2\right)}+g{L}_0-\left(L_0+x\right)g\end{array}}$

Para simplificar la ecuación diferencial, definimos las siguientes magnitudes

${\displaystyle \begin{array}{l}{\tilde{a}}_0=\frac{Q^2}{4{\pi }^2{\epsilon }_0}\frac{\left(k-1\right)\ln \frac{b}{a}}{\rho \left(b^2-a^2\right)L^{2}g}=g{\tilde{t}}_0{}^2\\ \xi =\frac{L_0+x}{{\tilde{a}}_0},\tau =\frac{t}{{\tilde{t}}_0},\alpha =\frac{L_0}{{\tilde{a}}_0},\sigma =\left(k-1\right)\frac{{\tilde{a}}_0}{L}\end{array}}$

El resultado es

${\displaystyle \begin{array}{l}{\tilde{a}}_0\xi \frac{{\tilde{a}}_0}{{\tilde{t}}_0^2}\frac{d^2\xi }{d{t}^2}+\frac{{\tilde{a}}_0^2}{{\tilde{t}}_0^2}{\left(\frac{dx}{dt}\right)}^2=\frac{g{L}^2{\tilde{a}}_0}{{\left(L+\left(k-1\right)\left(L_0+x\right)\right)}^2}+{\tilde{a}}_{0}g\alpha -{\tilde{a}}_0\xi g\\ \xi {\tilde{a}}_0\frac{d^2\xi }{d{\tau }^2}+{\tilde{a}}_0{\left(\frac{d\xi }{d\tau }\right)}^2=\frac{g{\tilde{t}}_0^2}{{\left(1+\left(k-1\right)\frac{\xi {\tilde{a}}_0}{L}\right)}^2}+\alpha g{\tilde{t}}_0^2-\xi g{\tilde{t}}_0^2\\ \xi \frac{d^2\xi }{d{\tau }^2}+{\left(\frac{d\xi }{d\tau }\right)}^2=\frac{1}{{\left(1+\sigma \xi \right)}^2}+\alpha -\xi \end{array}}$

Esta ecuación diferencial no tine solución analítica. Se resuelve aplicando procedimientos numéricos, con las condiciones iniciales, en el instante t=0, x=0, dx/dt=0. O bien, τ=0, ξ=L₀/a₀=α, p=dξ/dτ=0.

Referencias

Rafael Nardi, Nivaldo A Lemos. Dynamics of a liquid dielectric attracted by a cylindrical capacitor. Eur. J. Phys. 28 (2007) pp. 125-134

I. S. Gradshteyn, I. M. Ryzhik. Table of Integrals, Series, and Products. Seventh Edition. Elsevier (2007). Página 257, 3.132, n° 5