Se conectan dos condensadores
El caso más importante sucede cuando se conectan las placas del mismo signo de dos condensadores de capacidades C1 y C2. Si inicialmente, el condensador C1 se ha cargado con una carga Q y se conecta al condensador C2 inicialmente descargado. Después de conectarlos, las cargas pasan de un condensador al otro hasta que se igualan los potenciales.
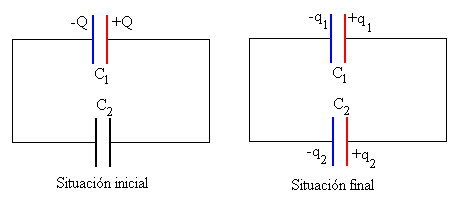
Las cargas finales de cada condensador q1 y q2, se obtienen a partir de las ecuaciones de la conservación de la carga y de la igualdad de potenciales de los condensadores después de la unión.
Despejando q1 y q2, en el sistema de dos ecuaciones
La energía inicial, es la almacenada en forma de campo eléctrico en el condensador de capacidad C1
La energía final, es la suma de las energías almacenadas en los dos condensadores
Como vemos la energía final Uf es menor que la inicial Ui.
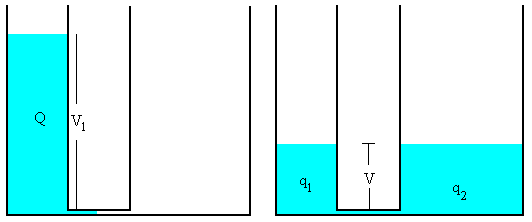
En la figura, se muestra la analogía hidráulica de un sistema formado por dos condensadores en paralelo.
Ejemplo:
Supongamos que tenemos un condensador cargado a una diferencia de potencial V, la carga que adquiere el condensador es Q0=C·V. La energía acumulada en el condensador es
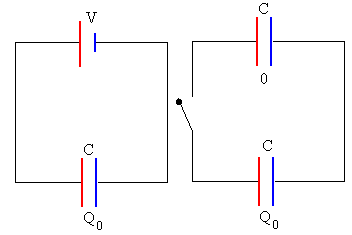
Conectamos este condensador a otro idéntico inicialmente descargado. Cuando el circuito se cierra la carga fluye del primero hacia el segundo hasta que la diferencia de potencial en ambos condensadores es la misma.
Como la capacidad C de ambos condensadores es la misma, la carga final de cada uno de los condensadores será la mitad de la carga inicial
La energía acumulada por el sistema formado por los dos condensadores es
La energía final es la mitad de la energía inicial. Siempre se perderá la mitad de la energía independientemente de que cambiemos o no la resistencia de los cables que unen los condensadores.
Analogía hidráulica
Supongamos dos depósitos cilíndricos iguales conectados por un tubo horizontal de sección despreciable, tal como se indica en la figura, el primero de ellos con una masa m de agua, y el segundo vacío.
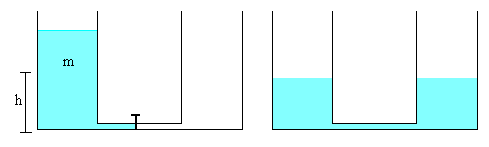
La energía inicial del agua es la energía potencial del centro de masas del agua que está a una altura h de la base. U0=mgh
Si se abre la llave, el agua fluye del primer depósito al segundo, hasta que la altura del agua es la misma en ambos. Por tanto, el agua se reparte por igual entre los dos depósitos. La energía final será
la mitad de la energía inicial.
Como hemos visto, si no hubiese resistencia alguna, no habría pérdidas, ya que la energía potencial del agua se transforma en cinética del agua que fluye y viceversa. El agua pasaría de un depósito al otro, se produciría un movimiento oscilatorio. Lo mismo ocurriría en un sistema de dos condensadores, la carga oscilaría entre los dos condensadores.
La resistencia del tubo, que conecta los dos depósitos, al movimiento del agua es análoga a la resistencia de los cables que conectan los dos condensadores, el primero se opone al flujo del agua, el segundo al flujo de carga. Después de unas cuantas oscilaciones se alcanza la situación final de equilibrio. En la página titulada El problema de los dos condensadores se describe este comportamiento oscilatorio
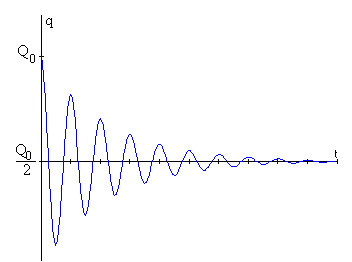
La situación final no se alcanza por tanto, de una vez, sino después de un cierto tiempo tanto más pequeño cuanto mayor sea la resistencia.
Circuito formado por dos condensadores y una resistencia
Consideremos el siguiente circuito formado por dos condensadores de capacidades C1 y C2 y una resistencia R.
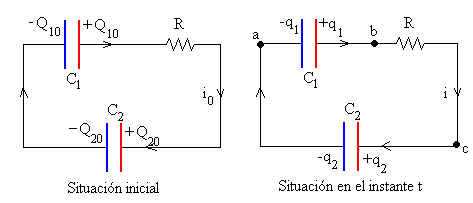
El condensador de capacidad C1 está cargado con una carga Q10 y el condensador de capacidad C2 está está cargado con una carga Q20. En el instante t=0, se cierra el circuito.
En un instante dado t, tendremos que
- El condensador C1 tiene una carga q1
- El condensador C2 tiene una carga q2
- Por la resistencia R circula una corriente de intensidad i.
Medimos las diferencias de potencial entre los puntos a y b, b y c, c y a. Se cumplirá que
Vab+Vbc+Vca=0
- En el condensador C1 el potencial de a (placa negativa) es menor que el b (placa positiva), de modo que Vab=-q1/C1
- En la resistencia R la corriente de intensidad i circula de b a c, luego Vbc=iR
- En el condensador C2 el potencial de c (placa positiva) es mayor que el a (placa negativa), de modo que Vca=q2/C2
La ecuación del circuito será
Supongamos que la carga q1 disminuye con el tiempo y la carga q2 aumenta con el tiempo, la intensidad i (carga por unidad de tiempo) valdrá
Derivamos la ecuación del circuito respecto del tiempo
Integramos la ecuación diferencial con la siguiente condición inicial: en el instante t=0, la intensidad i=i0.
En el instante inicial t=0, el condensador de capacidad C2 tiene una carga Q20, el condensador de capacidad C1 tiene una carga inicial Q10.
La solución de la ecuación diferencial es
Calculamos las cargas de cada condensador en función del tiempo con las siguientes condiciones iniciales: en el instante t=0, la carga del condensador C1 es q1=Q10, y la carga del condensador C2 es q2=Q20.
Como vemos q1+q2=Q10+Q20, la carga total en los condensadores es la carga inicial.
Después de un tiempo teóricamente infinito, se establece una situación de equilibrio en el que las cargas finales de los condensadores serán
Estudio energético
-
La energía inicial almacenada en los condensadores es
-
La energía final almacenada en los condensadores después de un tiempo teóricamente infinito es
-
La energía disipada en la resistencia R hasta que se establece la situación de equilibrio es
Parte de la energía inicial se disipa en la resistencia y la otra parte, se almacena en los condensadores en forma de campo eléctrico.
Uf=Ui-UR
Ejemplo:
- Resistencia, R=2
- Capacidad del primer condensador, C1=1
- Capacidad del segundo condensador, C2=1
- Carga inicial del primer condensador, Q10=5
- Carga inicial del segundo condensador, Q20=-3
-
Calcular la carga de cada condensador en el instante t=3, la energía inicial almacenada en los condensadores, la energía de los dos condensadores en dicho instante y la energía disipada en la resistencia.
-
Calcular la carga final de cada condensador en el instante t=∞, la energía final de los dos condensadores en dicho instante y la energía total disipada en la resistencia.
En el instante t=3, la carga de cada condensador es
La energía inicial y la energía almacenada en los condensadores en el instante t=3 es
La energía disipada en la resistencia hasta dicho instante vale
La carga final t→∞ de cada condensador vale
La energía final almacenada en los condensadores es
La energía total disipada en la resistencia vale
Como puede comprobarse
Uf=Ui-UR
Actividades
Se ha fijado
- la capacidad del primer condensador, C1=1
- la resistencia del circuito, R=2
Se introduce
- la capacidad del segundo condensador C2
- la carga inicial del primer condensador Q10
- la carga inicial del segundo condensador Q20
Se pulsa el botón titulado Nuevo
Se observa el movimiento de cargas entre los condensadores desde el estado inicial al estado final.

