En un condensador de plano-paralelo el campo no está confinado en el interior del condensador, sino que es intenso entre las placas y disminuye rápidamente fuera de las mismas. Si las placas están separadas una distancia pequeña en comparación con sus dimensiones, podemos considerar despreciable el campo fuera de las mismas.

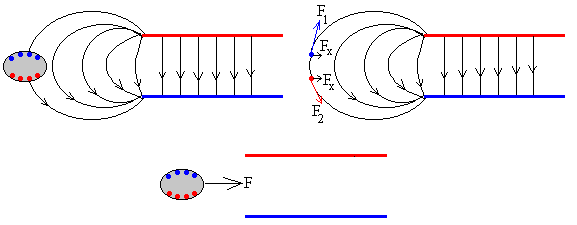
Sin embargo, este campo no homogéneo es el responsable de la atracción que experimenta un dieléctrico que se acerca a las proximidades de un condensador cargado.

Un dieléctrico en un campo eléctrico presenta cargas inducidas en su superficie, negativas cerca de la placa positiva y positivas cerca de la placa negativa. Como vemos en la figura la carga inducida negativa (positiva) está más cerca de la placa positiva (negativa) de la placa del condensador, existe una fuerza neta sobre el cuerpo dieléctrico que lo arrastra hacia el interior del condensador.

Si mantenemos V constante (la batería permanece conectada al condensador). La energía del condensador cargado es

${\displaystyle U=\frac{1}{2}C{V}^2}$

Vamos a calcular fuerza sobre el dieléctrico

• Si V permanece constante, al introducir el dieléctrico su capacidad C aumenta y su energía U aumenta.

${\displaystyle F_x={\left(\frac{\partial U}{\partial x}\right)}_V=\frac{1}{2}{V}^2\frac{\partial C}{\partial x}}$

La fuerza actúa en el sentido en el que aumenta la energía del condensador.

• Si se mantiene la carga Q fija (la batería carga al condensador y luego se desconecta).

${\displaystyle U=\frac{1}{2}{\frac{Q}{C}}^2}$

Si mantenemos Q constante al introducir el dieléctrico C aumenta y U disminuye.

${\displaystyle F_x=-{\left(\frac{\partial U}{\partial x}\right)}_Q=\frac{Q^2}{2C^2}\frac{\partial C}{\partial x}}$

El signo negativo indica que la fuerza tiene el sentido en el que disminuye la energía almacenada en el condensador

Descripción del experimento

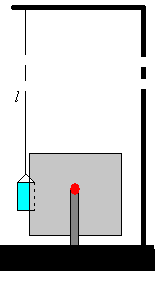
Un portaobjetos de vidrio es atraído hacia el interior de un condensador formado por dos placas paralelas. El portaobjetos está colgado de una larga cuerda, de modo que su desplazamiento x hacia el interior del condensador, nos da una medida de la fuerza sobre el dieléctrico.

Las placas del condensador de forma cuadrada tienen una dimensión de b=11.5 cm, están separadas una distancia d=2 mm y están conectadas a una fuente de modo que la diferencia de potencial entre las placas puede variar entre 1000 y 3000 V.

El portaobjetos de vidrio tiene un espesor t=1 mm, una altura de a=7.5 cm, una masa de m=4.37 g, y una constante dieléctrica k=5.

El portaobjetos está sujeto por una larga cuerda de modo que la distancia entre su centro y el punto de suspensión es de l=1.34 m.

En la experiencia real (véase el artículo citado en las referencias), la fuente suministra una diferencia de potencial alterna, debido a que con corriente continua las superficies del portaobjetos se polarizan y se pegan inmediatamente a una u otra placa del condensador.

Campo eléctrico

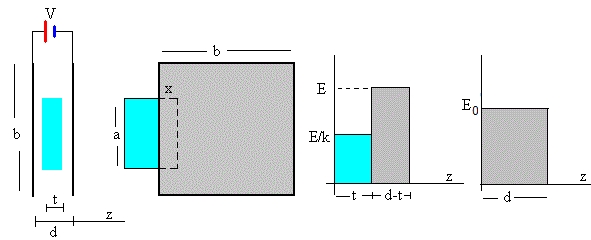
Las dos figuras de la izquierda representan el portaobjetos y las placas del condensador. El portaobjetos tiene un espesor t y la distancia entre las placas del condensador es d, tal como se muestra en la primera figura. El portaobjetos tiene una altura a y se ha introducido x entre las placas, tal como se muestra en la segunda figura.

Supondremos que el campo eléctrico en el interior del condensador plano-paralelo vacío E₀=V/d es constante y perpendicular a las placas y es despreciable fuera del condensador, tal como se muestra en la cuarta figura.

Cuando el dieléctrico se ha introducido una distancia x entre las placas del condensador, el campo en la región rectangular de dimensión a de alto y x de ancho cambia. En la tercera figura, se representa el campo eléctrico en dicha región en función de la distancia z a una de las placas. En el interior del dieléctrico, el campo se reduce a E/k, (k es la constante dieléctrica del material) y fuera del dieléctrico el campo es E. La suma de las áreas de los dos rectángulos es la diferencia de potencial constante V.

${\displaystyle V=\frac{E}{k}t+E(d-t)E=\frac{V}{d-(1-1/k)t}}$

Energía electrostática

Para hallar la energía electrostática dividimos el volumen del condensador en tres zonas.

• En la región del condensador vacía de área b²-ax y espesor d, el campo eléctrico es E₀=V/d, la energía electrostática es

${\displaystyle U_1=\left(\frac{1}{2}{\epsilon }_0{E}_0^2\right)(b^2-a·x)d=\frac{1}{2}{\epsilon }_0{V}^2\frac{b^2-ax}{d}}$

La región de área ax y espesor d, está dividida en dos partes:

• En la parte vacía de área ax y de espesor (d-t), el campo eléctrico es E, la energía electrostática es

${\displaystyle U_2=\left(\frac{1}{2}{\epsilon }_0{E}^2\right)ax·(d-t)=\frac{1}{2}{\epsilon }_0{\left(\frac{V}{d-(1-1/k)t}\right)}^{2}ax·(d-t)}$

• En la parte con dieléctrico de área ax y espesor t, el campo eléctrico es E/k¸la energía electrostática es

${\displaystyle U_3=\left(\frac{1}{2}k{\epsilon }_0\frac{E^2}{k^2}\right)ax·t=\frac{1}{2}{\epsilon }_0{\left(\frac{V}{d-(1-1/k)t}\right)}^2\frac{ax·t}{k}}$

La energía electrostática total U es la suma de las tres contribuciones U=U₁+U₂+U₃.

Fuerza sobre el dieléctrico

Como la diferencia de potencial V se mantiene constante mientras se introduce el dieléctrico en el condensador. La fuerza sobre el portaobjetos es

${\displaystyle F={\left(\frac{\partial U}{\partial x}\right)}_V=-\frac{1}{2}{\epsilon }_0{V}^2\frac{a}{d}+\frac{1}{2}{\epsilon }_0{V}^2\frac{a}{d-(1-1/k)t}}$

Equilibrio del portaobjetos

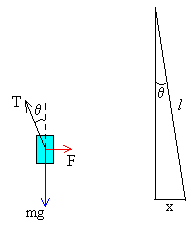
El portaobjetos está en equilibrio bajo la acción de las siguientes fuerzas:

• El peso mg

• La fuerza de atracción F, horizontal y dirigida hacia el interior del condensador

• La fuerza que ejerce la cuerda T.

Como consecuencia, el hilo se desvía de la vertical un ángulo θ.

T·sinθ=F
T·cosθ=mg

El desplazamiento x del portaobjetos es

${\displaystyle \sin \theta =\frac{x}{l}\text{tan}\theta =\frac{F}{mg}}$

Como la distancia entre le centro del portaobjetos y el punto de suspensión l es muy grande comparado con el desplazamiento x del portaobjetos, el ángulo θ es pequeño,

${\displaystyle \sin \theta \approx \tan \theta x=\frac{F·l}{mg}}$

Actividades

Se introduce

• La diferencia de potencial V constante entre las placas del condensador, en el control titulado Diferencia de potencial.

Se pulsa el botón titulado Nuevo

Se observa el desplazamiento x del portaobjetos hacia el interior del condensador, y se mide en la escala graduada en cm.

Datos que se mantienen fijos en el programa interactivo son:

• Distancia entre las placas del condensador d=2mm
• Altura del portaobjetos a=7.5 cm
• Espesor del portaobjetos t=1 mm
• Constante dieléctrica del vidrio k=5
• Distancia entre el centro del portaobjetos y el punto de suspensión l=134 cm
• Masa del portaobjetos m=4.37 g

Cuando V=2000 V

${\displaystyle F=\frac{1}{2}\frac{1}{4\pi ·9·{10}^9}{2000}^2\left(-\frac{0.075}{0.002}+\frac{0.075}{0.002-(1-\frac{1}{5})0.001}\right)=4.42·{10}^{-4}\text{N}}$

El ángulo θ de desviación de la cuerda de su posición inicial es

${\displaystyle \tan \theta =\frac{4.42·{10}^{-4}}{4.37·{10}^{-3}·9.8}\theta =0.59º}$

La desviación x es

x=l·sinθ=134·sin0.59º=1.38 cm

Referencias

Benenson R. E. Direct observation of the force on a dielectric. Am. J. Phys. 59 (8) August 1991, pp. 763-764