Un oscilador eléctrico (carga constante)
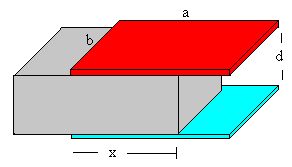
Supongamos un condensador plano-paralelo cargado con carga Q mediante una batería y a continuación se desconectan las placas. Las dimensiones del condensador son a y b, y d es la separación entre las placas.
La capacidad del condensador vacío es
La energía almacenada en el condensador es
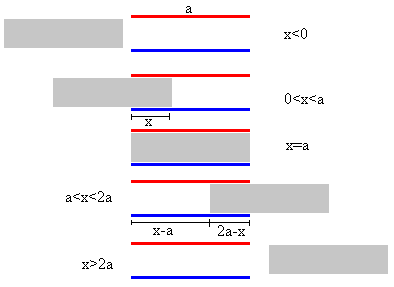
Supongamos que el dieléctrico ha penetrado una longitud x<a en el condensador inicialmente vacío. Para hallar la capacidad del condensador con dieléctrico podemos considerar el condensador como la agrupación de dos condensadores en paralelo, uno con dieléctrico de longitud x y otro, en el vacío de longitud a-x. Tenemos que la capacidad total de la agrupación es la suma de las capacidades de cada uno de los condensadores planos-paralelos.
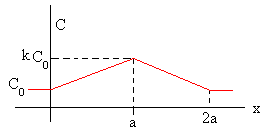
La capacidad se incrementa al introducirse el dieléctrico hasta que alcanza un máximo valor k·C0 cuando el dieléctrico ocupa todo el espacio entre las dos placas paralelas.
La energía U del condensador es una función de x.
La energía disminuye a medida que x aumenta. La energía mínima se obtiene cuando todo el dieléctrico x=a ocupa el espacio entre las placas del condensador.
Carga constante
La fuerza se obtiene derivando la energía U, manteniendo la carga constante (el condensador no está conectado a la batería)
La fuerza actúa en el sentido en el que tiende a disminuir la energía U almacenada en el sistema
En la tabla se resume los valores de la capacidad C, energía electrostática U y la fuerza F sobre el dieléctrico para distintas posiciones x.
| Posición | Capacidad | Energía electrostática | Fuerza |
|---|---|---|---|
| x<0 | F=0 | ||
| 0<x<a | |||
| x=a | C=k·C0 | ||
| a<x<2a | |||
| x>2a | F=0 |
La capacidad C es simétrica respecto de x=a. El valor de la capacidad C, de la energía electrostática U y el módulo de la fuerza F es el mismo para x=a-δ y para x=a+δ. Como vemos en las gráficas, arriba de la capacidad y más abajo, de la energía U y de la fuerza F.
Discusión
En la posición x=a, la energía potencial presenta un mínimo. La derivada debería de ser cero. Sin embargo, la fuerza F en x=a no da cero
Esta discrepancia se debe a que la energía potencial U es discontinua en x=a y por tanto, la función energía potencial U no es diferenciable en este punto.
En realidad, la energía potencial U es continua, ya que en nuestro modelo simplificado no se han tenido en cuenta el campo eléctrico existente fuera del condensador y su contribución a la energía potencial eléctrica.
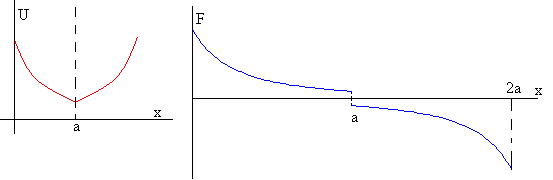
El cálculo que hemos realizado, tal como se presenta en la mayoría de los libros de texto, ignora el origen físico de la fuerza de atracción sobre el dieléctrico. ¿Cómo puede atraer el campo eléctrico de un condensador al dieléctrico, si el campo eléctrico es perpendicular a las placas y solamente existe en la región situada entre las mismas?, tal como se muestra en la figura de la izquierda
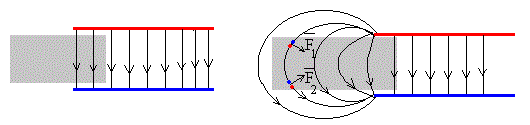
La fuerza sobre el dieléctrico es debida al campo existente fuera del dieléctrico Así, consideremos dos moléculas del dieléctrico, polarizadas por el campo existente fuera del condensador y dispuestas simétricamente, como se muestra en la figura de la derecha. Las fuerzas sobre cada una de las dos cargas de una molécula son tangentes a la línea de fuerza en el punto en la que está situadas las cargas y son opuestas pero no son completamente colineales y por tanto, existe una fuerza resultante sobre cada molécula que representamos por y .
La fuerza neta sobre el par de moléculas está dirigida hacia la derecha. La fuerza sobre el dieléctrico es la suma de las fuerzas que ejerce el campo eléctrico sobre todos los pares de moléculas.
Actividades
Una pieza de material dieléctrico es atraída hacia el interior del condensador, su energía potencial eléctrica se convierte en energía cinética. Alcanza la máxima velocidad cuando ocupa todo el espacio entre las placas y luego, comienza a salir, su energía cinética se convierte en potencial eléctrica y así sucesivamente.
Tenemos un oscilador, pero no es un oscilador armónico, ya que no describe un MAS, la fuerza no es proporcional al desplazamiento x. La posición del diléctrico x en función del tiempo t se determina resolviendo numéricamente las ecuación del movimiento.
Elegimos una sustancia dieléctrica en una lista de sustancias:
| Sustancia | cte. dieléctrica | Sustancia | cte. dieléctrica |
|---|---|---|---|
| Ambar | 2.8 | Plástico | 4.1 |
| Baquelita | 4.3 | Porcelana | 6.0 |
| Parafina | 2.2 | Pexiglás | 3.3 |
Se pulsa el botón titulado Nuevo
Se observa el movimiento de la pieza dieléctrica entre las placas del condensador. Se muestra mediante un vector la fuerza sobre la pieza y su energía potencial eléctrica para cada posición x del dieléctrico.
Ejemplo:
En la parte izquierda, se muestra el condensador, conectado a un voltímetro. La carga Q no cambia, pero al introducirse el dieléctrico la capacidad se modifica.
En el programa interactivo, la longitud del condensador se ha fijado en a=10, y Q/C0=1 se ha tomado igual a la unidad. Por ejemplo, eligiendo el ámbar como sustancia dieléctrica k=2.8 y para x=2, el potencial vale
Para x=20-2=18, el potencial V tiene el mismo valor que para x=2.
El potencial es mínimo V=0.36, para x=10.

