Carga de un condensador

El circuito que representa la carga de un condensador real sería el siguiente.

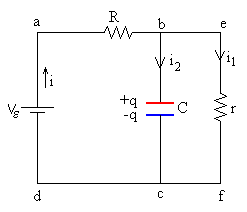
Donde r es la resistencia interna del condensador.

Las ecuaciones son

${\displaystyle \begin{array}{l}{V}_{ab}+V_{bc}+V_{cd}+V_{da}=0iR+\frac{q}{C}-V_{\epsilon }=0\\ V_{ae}+V_{ef}+V_{fd}+V_{da}=0iR+i_{1}r-V_{\epsilon }=0\\ i=i_1+i_2\end{array}}$

Despejamos del sistema de ecuaciones las intensidades i₁ e i₂

${\displaystyle i_1=\frac{q}{rC}{i}_2=\frac{1}{R}\left[V_{\epsilon }-\frac{q}{C}\left(1+\frac{R}{r}\right)\right]}$

Teniendo en cuanta que i₂=dq/dt, calculamos la carga q del condensador en función del tiempo t, sabiendo que en el instante t=0, q=0, el condensador está inicialmente descargado.

${\displaystyle \begin{array}{l}\frac{dq}{dt}=a-bq{\displaystyle \underset{0}{\overset{q}{\int }}\frac{dq}{a-bq}}={\displaystyle \underset{0}{\overset{t}{\int }}dt}\\ q=\frac{a}{b}\left(1-\exp (-bt)\right)\\ q=\frac{r}{r+R}{V}_{\epsilon }C\left(1-\exp \left(-\frac{t}{\tau }\right)\right)\tau =\frac{1}{b}=\frac{rR}{r+R}C\end{array}}$

Las intensidades valen

${\displaystyle \begin{array}{l}{i}_2=\frac{dq}{dt}=\frac{V_{\epsilon }}{R}\exp \left(-\frac{t}{\tau }\right)i_1=\frac{q}{rC}=\frac{V_{\epsilon }}{r+R}\left(1-\exp \left(-\frac{t}{\tau }\right)\right)\\ i=i_1+i_2=\frac{V_{\epsilon }}{r+R}\left(1+\frac{r}{R}\exp \left(-\frac{t}{\tau }\right)\right)\end{array}}$

Energías

Energía almacenada en el condensador en el instante t

${\displaystyle E_C=\frac{1}{2}\frac{q^2}{C}=\frac{1}{2}{\left(\frac{V_{\epsilon }r}{r+R}\right)}^{2}C{\left(1-\exp \left(-\frac{t}{\tau }\right)\right)}^2}$

Energía disipada en la resistencia interna r.

${\displaystyle \begin{array}{l}{E}_r={{\displaystyle \underset{0}{\overset{t}{\int }}{i}_1^{2}r·dt={\displaystyle \underset{0}{\overset{t}{\int }}r{\left(\frac{V_{\epsilon }}{r+R}\right)}^2\left(1-\exp \left(-\frac{t}{\tau }\right)\right)}}}^{2}dt=\\ r{\left(\frac{V_{\epsilon }}{r+R}\right)}^2\left(t-\frac{\tau }{2}\exp \left(-\frac{2t}{\tau }\right)+2\tau \exp \left(-\frac{t}{\tau }\right)-\frac{3}{2}\tau \right)\end{array}}$

Energía disipada en la resistencia R.

${\displaystyle \begin{array}{l}{E}_R={\displaystyle \underset{0}{\overset{t}{\int }}{i}^{2}R·dt={\displaystyle \underset{0}{\overset{t}{\int }}R}}{\left(\frac{V_{\epsilon }}{r+R}\right)}^2{\left(1+\frac{r}{R}\exp \left(-\frac{t}{\tau }\right)\right)}^{2}dt=\\ R{\left(\frac{V_{\epsilon }}{r+R}\right)}^2\left(t-\frac{\tau }{2}\frac{r^2}{R^2}\exp \left(-\frac{2t}{\tau }\right)-2\frac{r}{R}\tau \exp \left(-\frac{t}{\tau }\right)+\frac{\tau }{2}\frac{r^2}{R^2}+2\frac{r}{R}\tau \right)\end{array}}$

Energía suministrada por la batería

${\displaystyle \begin{array}{l}{E}_{\epsilon }={\displaystyle \underset{0}{\overset{t}{\int }}{V}_{\epsilon }i·dt={\displaystyle \underset{0}{\overset{t}{\int }}\frac{V_{\epsilon }^2}{r+R}\left(1+\frac{r}{R}\exp \left(-\frac{t}{\tau }\right)\right)}}dt=\\ \frac{V_{\epsilon }^2}{r+R}\left(t-\frac{r}{R}\tau \exp \left(-\frac{t}{\tau }\right)+\frac{r}{R}\tau \right)\end{array}}$

Comprobamos que parte de la energía suministrada por la batería E_ε, se almacena en el condensador E_C y otra parte, se disipa en la resistencia interna E_r y externa E_R.

E_ε=E_R+E_r+E_C

Después de un tiempo grande exp(-t/τ) tiende a cero

La carga máxima del condensador es

${\displaystyle q_{máx}=\frac{r}{r+R}{V}_{\epsilon }C}$

y la energía acumulada en el condensador es

${\displaystyle E_C=\frac{1}{2}\frac{q_{máx}^2}{C}=\frac{1}{2}{\left(\frac{r}{r+R}\right)}^2{V}_{\epsilon }^{2}C}$

Descarga de un condensador real

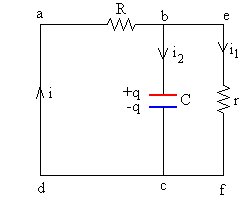
Las ecuaciones son

${\displaystyle \begin{array}{l}{V}_{ab}+V_{bc}+V_{cd}+V_{da}=0iR+\frac{q}{C}=0\\ V_{ae}+V_{ef}+V_{fd}+V_{da}=0iR+i_{1}r=0\\ i=i_1+i_2\end{array}}$

Despejamos del sistema de ecuaciones las intensidades i₁ e i₂

${\displaystyle i_1=\frac{q}{rC}{i}_2=-\frac{q}{C}\left(\frac{1}{R}+\frac{1}{r}\right)}$

Teniendo en cuanta que i₂=dq/dt, calculamos la carga q del condensador en función del tiempo t, sabiendo que en el instante t=0, q=q₀, el condensador está inicialmente cargado.

${\displaystyle \begin{array}{l}\frac{dq}{dt}=-bq{\displaystyle \underset{q_0}{\overset{q}{\int }}\frac{dq}{q}}=-b{\displaystyle \underset{0}{\overset{t}{\int }}dt}\\ q=q_0\exp (-bt)\\ q=q_0\exp \left(-\frac{t}{\tau }\right)\tau =\frac{1}{b}=\frac{rR}{r+R}C\end{array}}$

Las intensidades valen

${\displaystyle \begin{array}{l}{i}_2=\frac{dq}{dt}=-\frac{q_0}{C}\frac{r+R}{rR}\exp \left(-\frac{t}{\tau }\right)i_1=\frac{q}{rC}=\frac{q_0}{rC}\exp \left(-\frac{t}{\tau }\right)\\ i=i_1+i_2=-\frac{q_0}{CR}\exp \left(-\frac{t}{\tau }\right)\end{array}}$

Energías

Energía almacenada en el condensador en el instante inicial

${\displaystyle E_C=\frac{1}{2}\frac{q_0^2}{C}}$

Energía disipada en la resistencia interna r.

${\displaystyle \begin{array}{l}{E}_r={{\displaystyle \underset{0}{\overset{t}{\int }}{i}_1^{2}r·dt={\displaystyle \underset{0}{\overset{t}{\int }}r\left(\frac{q_0}{rC}\exp \left(-\frac{t}{\tau }\right)\right)}}}^{2}dt=\\ \frac{1}{r}{\left(\frac{q_0}{C}\right)}^2\left(\frac{\tau }{2}-\frac{\tau }{2}\exp \left(-\frac{2t}{\tau }\right)\right)\end{array}}$

Energía disipada en la resistencia R.

${\displaystyle \begin{array}{l}{E}_R={\displaystyle \underset{0}{\overset{t}{\int }}{i}^{2}R·dt={\displaystyle \underset{0}{\overset{t}{\int }}R}}{\left(-\frac{q_0}{CR}\exp \left(-\frac{t}{\tau }\right)\right)}^{2}dt=\\ \frac{1}{R}{\left(\frac{q_0}{C}\right)}^2\left(\frac{\tau }{2}-\frac{\tau }{2}\exp \left(-\frac{2t}{\tau }\right)\right)\end{array}}$

Comprobamos que la energía suministrada por el condensador se disipa en las dos resistencias

${\displaystyle \begin{array}{l}\Delta E_C=\frac{1}{2}\frac{q_0^2}{C}-\frac{1}{2}\frac{q^2}{C}=\frac{1}{2}\frac{q_0^2}{C}\left(1-\exp \left(-\frac{2t}{\tau }\right)\right)\\ \Delta E_C=E_r+E_R\end{array}}$

Después de un tiempo grande exp(-2t/τ) tiende a cero

La energía almacenada en el condensador se disipa en las dos resistencias.

E_C=E_r∞+E_R∞

Referencias

Carvalho P. S., Sampaio e Sousa A., Helping students understand real capacitors: measuring efficiencies in a school laboratory. Physics Education 43 (4) July 2008, pp. 400-406.