Condensador cargado aislado

Ente las placas de un condensador plano-paralelo, se coloca un péndulo, atando al extremo de un hilo una pequeña esfera de metal normalmente, una bolita que se ha hecho plegando con los dedos papel de aluminio.

Una de las placas del condensador se conecta a un electroscopio, la otra placa se conecta a tierra.

Ponemos en marcha un generador de Van de Graaff y transportamos carga desde la esfera del generador a la placa del condensador conectada al espectroscopio mediante una bola metálica situada en el extremo de una varilla de plástico, o bien, conectamos con un cable esta placa con la esfera del generador.

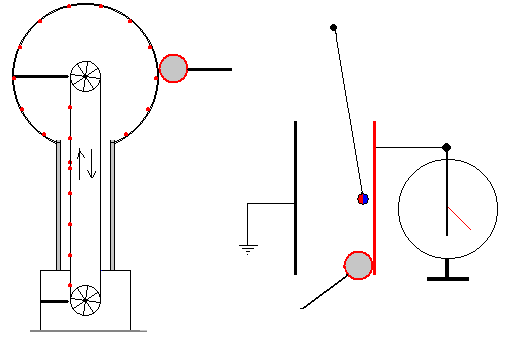
En el primer caso, la placa se va cargando, la aguja del electroscopio se va desviando de su posición de equilibrio. La bolita metálica es atraída hacia la placa cargada. En un momento dado entra en contacto con ella y el péndulo empieza a moverse rápidamente entre las placas del condensador, descargando la placa unida al electroscopio.

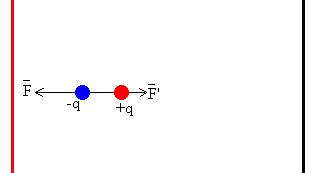
Como vemos en la figura, la placa positiva del condensador está más cerca de la carga negativa inducida en la bolita, que de la carga positiva inducida en la misma. Luego, la fuerza neta será atractiva.

Cuando el campo es suficientemente intenso, la bolita toca la placa positiva del condensador. La bolita se carga con una carga positiva Δq y placa pierde la misma carga que ha adquirido la bolita.

El electroscopio indicará la disminución de carga de la placa, la aguja indicadora formará ahora un ángulo ligeramente más pequeño con la vertical.

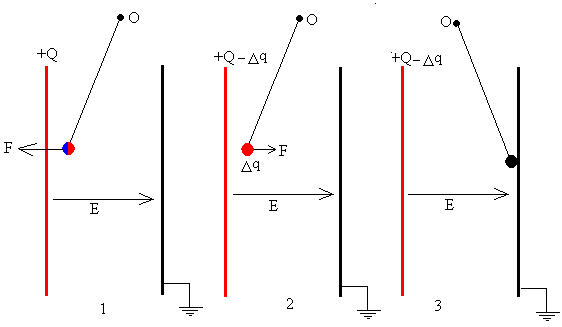
Una vez que la bolita se ha cargado positivamente, experimenta una fuerza en el sentido del campo, que la mueve rápidamente hacia la placa opuesta conectada a tierra.

La bolita choca con dicha placa y pierde entonces su carga. Rebota y se mueve hacia la posición de equilibrio, rebasándola debido a su energía cinética y comienza un nuevo ciclo.

El resultado es que la placa positiva va perdiendo una carga Δq, cada vez que la bolita entra en contacto con dicha placa. El electroscopio indicará la disminución paulatina de carga en la placa.

Cuando la carga existente en la placa está por debajo de cierto valor, el campo eléctrico entre las placas es pequeño y la bolita es atraída por la placa positiva con una fuerza que no es suficiente para que entre en contacto con ella. La bolita oscila cada vez con menos amplitud debido al rozamiento con el aire hasta que se detiene.

Actividades

Disponemos de un generador de Van de Graaff para suministrar la carga que transportamos a una de las placas del condensador.

• Se pulsa el botón titulado Nuevo
• Pulsamos varias veces el botón titulado Carga para repetir la operación de carga del condensador

Vemos como se va cargando la placa y se desvía la aguja indicadora del electroscopio. La bolita es atraída hacia la placa positiva, hasta que entra en contacto con ella. En ese momento, la bolita empieza a oscilar y la placa positiva del condensador empieza a perder poco a poco carga en cada oscilación de la bolita.

Para repetir la experiencia se pulsa el botón titulado Nuevo.

Condensador conectado a una batería

En primer lugar, no tendremos en cuenta el peso de la bolita conductora que se moverá horiontalmente hacia adelante y hacia atrás chocando con las placas.

En una segunda aproximación, tendremos en cuenta el efecto de la componente tangencial del peso y calcularemos la frecuencia final en el estado estacionario.

En este análisis no tendremos en cuenta el efecto del rozamiento del la bolita al moverse en el aire

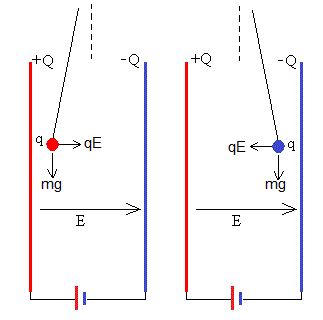
Un condensador plano paralelo se conecta a una batería V₀ que suministra una carga Q a las placas. Un pequeño conductor de masa m se suspende de un hilo muy largo y se coloca entre las placas del condensador de área S separadas una distancia d.

El pequeño conductor describe un arco de circunferencia bajo la acción de dos fuerzas: el peso mg y la fuerza que ejerce el campo eléctrico E sobre la carga q.

Inicialmente, el conductor se pone en contacto con la placa positiva y adquiere una carga q del mismo signo. Se mueve hacia la placa negativa, choca con dicha placa cambiando el módulo y el sentido de su velocidad. Mientras está en contacto con la placa negativa adquiere una carga q del mismo signo que la placa. El conductor inicia el viaje de vuelta hacia la placa positiva, choca con dicha placa adquiriendo una carga q del mismo signo, cambiando el módulo y el sentido de su velocidad. Completándose el primer periodo de la oscilación de la bolita cargada.

Movimiento de la bolita cargada en un campo eléctrico uniforme

La fuerza que ejerce el campo eléctrico E existente entre las placas del condensador es qE=qV₀/d y la aceleración a=qE/m

Sea q una fracción r de la carga Q de las placas

${\displaystyle a=\frac{rQ{V}_0}{md}=\frac{rC{V}_0^2}{md}={\epsilon }_0\frac{rS}{m}{\left(\frac{V_0}{d}\right)}^2}$

donde C=ε₀S/d es la capacidad del condensador plano-paralelo

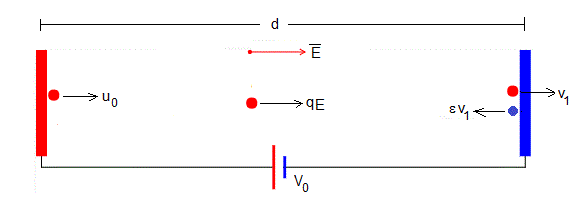
Supongamos que la bolita conductora se suelta cuando está en contacto con la placa positiva, es acelerada por el campo eléctrico E una distancia d hasta que llega a la placa negativa

La velocidad inicial, cuando la bolita se pone en contacto con la placa positiva es u₀=0. La velocidad final v₁ cuando alcanza la placa opuesta es

${\displaystyle \begin{array}{l}{v}_1=u_0+at\\ d=u_{0}t+\frac{1}{2}a{t}^2\end{array}\}{v}_1^2=u_0^2+2ad}$

Cuando la bolita choca con la placa cambia el sentido de su velocidad, su módulo y el signo de la carga. Si el coeficiente de restitución es ε<1, la velocidad inmediatamente después del choque será menor ε·v₁

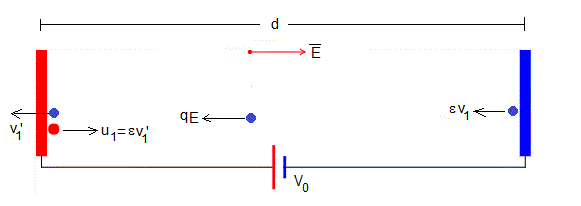
La bolita cargada con una carga q negativa inicia el viaje de vuelta impulsada por el campo eléctrico E. La velocidad v'₁ que tiene al establecer contacto con la placa positiva es

${\displaystyle \begin{array}{l}{v}_1^{\text{'}2}={\left(\epsilon v_1\right)}^2+2ad\\ v_1^{\text{'}2}={\epsilon }^2{u}_0^2+2ad\left(1+{\epsilon }^2\right)\end{array}}$

Cuando la bolita choca con la placa cambia el sentido de su velocidad, su módulo y el signo de la carga. La velocidad inmediatamente después del choque será u₁=ε·v'₁

${\displaystyle u_1^2={\epsilon }^4{u}_0^2+2ad\left({\epsilon }^2+{\epsilon }^4\right)}$

con lo que se completa el primer periodo

La bolita cargada con una carga q positiva inicia el viaje de ida impulsada por el campo eléctrico E. La velocidad v₂ que tiene al establecer contacto con la placa negativa es

${\displaystyle v_2^2=u_1^2+2ad={\epsilon }^4{u}_0^2+2ad\left(1+{\epsilon }^2+{\epsilon }^4\right)}$

La velocidad inmediatamente después del choque es ε·v₂. La bolita cargada con una carga q negativa inicia el viaje de vuelta impulsada por el campo eléctrico E. La velocidad v'₂ que tiene al establecer contacto con la placa positiva es

${\displaystyle v_2^{\text{'}2}={\epsilon }^6{u}_0^2+2ad\left(1+{\epsilon }^2+{\epsilon }^4+{\epsilon }^6\right)}$

La velocidad inmediatamente después del choque será u₂=ε·v'₂

${\displaystyle u_2^2={\epsilon }^8{u}_0^2+2ad\left({\epsilon }^2+{\epsilon }^4+{\epsilon }^6+{\epsilon }^8\right)}$

con lo que se completa el segundo periodo

Después de n periodos

${\displaystyle u_n^2={\epsilon }^{4n}{u}_0^2+2ad\left({\epsilon }^2+{\epsilon }^4+\mathrm{...}+{\epsilon }^{4n}\right)}$

N=10;
e=0.9;
y=zeros(1,N);
for n=1:N
    y(n)=sum((e.^(2:2:4*n)));
end
plot(0:N,[0,y],'o','markersize',4,'markeredgecolor',
'r','markerfacecolor','r')
grid on
xlabel('n')
ylabel('u')
title('Hacia el estado estacionario')

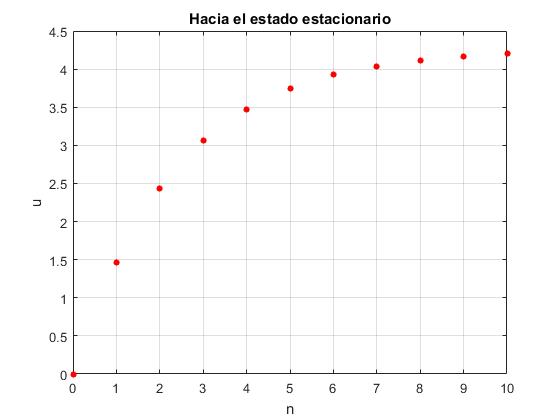
Cuando n tiende a infinito, el primer término tiende a cero ya que ε<1. El término entre paréntesis es la suma de infinitos términos de una progresión geométrica cuyo primer término es ε² y la razón es ε²

${\displaystyle u_{\infty }^2=2ad\frac{{\epsilon }^2}{1-{\epsilon }^2}}$

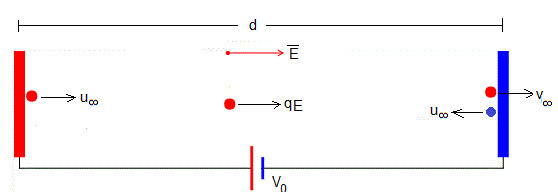
Una vez que se ha alcanzado el estado estacionario, la velocidad después de de chocar con la placa es u_∞ y la velocidad antes de chocar con la placa opuesta es u_∞+a·Δt, donde Δt es el tiempo que tarda la bolita en viajar de una placa a la otra.

${\displaystyle \begin{array}{l}{\left(u_{\infty }+a\Delta t\right)}^2=u_{\infty }^2+2ad\\ \Delta t=\sqrt{\frac{2d\left(1-\epsilon \right)}{a\left(1+\epsilon \right)}}\end{array}}$

Comprobamos que en el estado estacionario, el incremento de la velocidad de la bolita durante su viaje entre las dos placas u_∞+a·Δt se pierde en el choque

${\displaystyle u_{\infty }=\epsilon \left(u_{\infty }+a\Delta t\right)}$

El periodo P y la frecuencia f son, respectivamente

${\displaystyle \begin{array}{l}P=2\Delta t\\ f=\frac{1}{2}\sqrt{\frac{a\left(1+\epsilon \right)}{2d\left(1-\epsilon \right)}}=k\left(\frac{V_0}{d}\right)\end{array}}$

La frecuencia es proporcional al campo E=V₀/d existente entre las placas del condensador

Actividades

Se introduce

• El coeficiente de restitución, e, en el control titulado Coef. restitución

• La diferencia de potencial entre las placas, V, en el control titulado d.d.p.

Se representa la velocidad u_n en función del tiempo t. Vemos que la velocidad final tiene hacia un valor límite constante u_∞. Esta velocidad es proporcional a la diferencia de potencial V₀ entre las placas del condensador

La bolita conductora se mueve bajo la acción de su peso y de la fuerza que produce el campo eléctrico

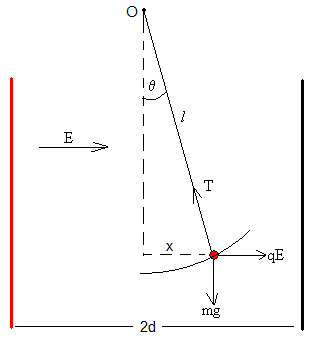
Las fuerzas sobre la bolita cargada son:

• El peso, mg
• La fuerza que ejerce el campo eléctrico, qE
• La tensión de la cuerda, T

Descomponemos las fuerzas en la dirección tangencial y en la dirección normal

La ecuación del movimiento de la bolita es

${\displaystyle ml\frac{d^2\theta }{d{t}^2}=-mg\sin \theta +qE\cos \theta }$

Si la separación 2d entre las placas es pequeña comparada con la longitud l del péndulo, la amplitud de la oscilación del péndulo es pequeña, hacemos las siguientes aproximaciones

sinθ≈θ, cosθ≈1

La ecuación del movimiento se escribe

${\displaystyle \begin{array}{l}\frac{d^2(l\theta )}{d{t}^2}+\frac{g}{l}x=\frac{qE}{m}\\ \frac{d^{2}x}{d{t}^2}+{\omega }^{2}x=\frac{qE}{m}\end{array}}$

La solución de esta ecuación diferencial es

${\displaystyle \begin{array}{l}x=A\sin \left(\omega t\right)+B\cos \left(\omega t\right)+C\\ \frac{dx}{dt}=\omega \left(A\cos \left(\omega t\right)-B\sin \left(\omega t\right)\right)\end{array}}$

La constante C es la solución particular ω²C=qE/m

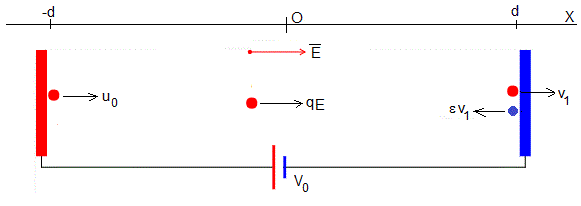
Los coeficientes A y B se determinan a partir de las condiciones iniciales: en el instante t=0, la posición es x=-d,dx/dt=u₀

${\displaystyle \begin{array}{l}x=\frac{u_0}{\omega }\sin (\omega t)-\left(d+\delta \right)\cos (\omega t)+\delta \\ \frac{dx}{dt}=u_0\cos (\omega t)+\omega \left(d+\delta \right)\sin (\omega t)\end{array}}$

con δ=qE/mω²

Para calcular el tiempo t₁ que tarda la bolita en alcanzar la placa negativa x=d utilizamos la equivalencia, Asin(ωt)+Bcos(ωt)=Msin(ωt+φ)

${\displaystyle \begin{array}{l}d-\delta =M\sin \left(\omega t+\phi \right)\{\begin{array}{l}M\cos \phi =u_0/\omega \\ M\sin \phi =-(d+\delta )\end{array}\\ t_1=\frac{1}{\omega }\left(\arcsin \left(\frac{d-\delta }{\sqrt{{\left(u_0/\omega \right)}^2+{\left(d+\delta \right)}^2}}\right)+\arctan \left(\frac{d+\delta }{u_0/\omega }\right)\right)\end{array}}$

La bolita alcanza la velocidad v₁ al llegar a la placa negativa

${\displaystyle v_1=u_0\cos (\omega t_1)+\omega \left(d+\delta \right)\sin (\omega t_1)}$

Después del choque la bolita cambia el módulo, el sentido de su velocidad y el signo de la carga, ε·v₁

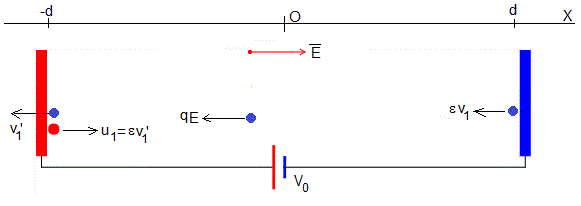
Ponemos el reloj a cero t=0, y calculamos el tiempo t₂ que tarda la bolita en moverse desde la placa negativa x=d hasta la placa positiva x=-d

Las condiciones iniciales son ahora: el instante t=0, la posición de la bolita es x=d y su velocidad es -ε·v₁. Dado que la carga q ha cambiado de signo, la ecuación del movimiento es

${\displaystyle \begin{array}{l}x=-\frac{\epsilon v_1}{\omega }\sin (\omega t)+\left(d+\delta \right)\cos (\omega t)-\delta \\ \frac{dx}{dt}=-\epsilon v_1\cos (\omega t)-\omega \left(d+\delta \right)\sin (\omega t)\end{array}}$

con δ=|q|E/mω²

Calculamos el tiempo t₂ que tarda la bolita en llegar a la posición x=-d

${\displaystyle $ t_2=\frac{1}{\omega }\left(\arcsin \left(\frac{d-\delta }{\sqrt{{\left(\epsilon v_1/\omega \right)}^2+{\left(d+\delta \right)}^2}}\right)+\arctan \left(\frac{d+\delta }{\epsilon v_1/\omega }\right)\right)$}$

Inmediatamente después del choque con la placa positiva, la velcidad u₁ de la bolita es

${\displaystyle \begin{array}{l}{u}_1=-\epsilon \left(-\epsilon v_1\cos (\omega t_2)-\omega \left(d+\delta \right)\sin (\omega t_2)\right)=\\ {\epsilon }^2{v}_1\cos (\omega t_2)+\epsilon \omega \left(d+\delta \right)\sin (\omega t_2)\end{array}}$

Esta es la velocidad inicial para el siguiente periodo

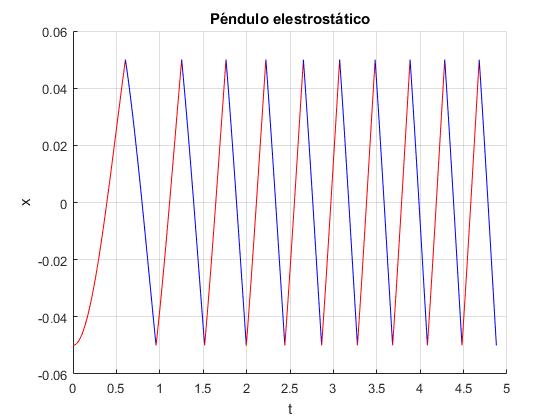
Representamos la posición x de la bolita en función del tiempo t

d=0.05; %mitad de la separación entre placas
e=0.9; %coeficente de restituación
ddp=250000; %fem de la batería
w=sqrt(9.8); % el péndulo tiene una longitud de  1 m.

delta=(ddp/(4*d))^2/(4*pi*9e9*2700*0.02*w^2);
N=10; %periodos
v0=0;
P=0;
hold on
for i=1:N
    t1=(asin((d-delta)/sqrt((v0/w)^2+(d+delta)^2))+atan((d+delta)/(v0/w)))/w; 
    x1=@(t) (v0/w)*sin(w*t)-(d+delta)*cos(w*t)+delta;
    v1=@(t) v0*cos(w*t)+w*(d+delta)*sin(w*t);
    [tt,y]=fplot(x1,[0,t1]);
    plot(tt+P,y, 'r');
    P=P+t1;

    v0=-e*v1(t1);
    t2=(asin((d-delta)/sqrt((v0/w)^2+(d+delta)^2))+atan((d+delta)/(-v0/w)))/w;
    x2= @(t) (v0/w)*sin(w*t)+(d+delta)*cos(w*t)-delta;
    v2= @(t) v0*cos(w*t)-w*(d+delta)*sin(w*t);
    [tt,y]=fplot(x2,[0,t2]);
    plot(tt+P,y, 'b');
    P=P+t2;
    v0=-e*v2(t2);
end
hold off
grid on
xlabel('t')
ylabel('x')
title('Péndulo elestrostático')

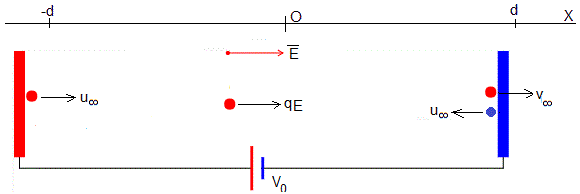
En el estado estacionario, la bolita sale de la placa positiva x=-d con velocidad u_∞ y llega a la placa negativa x=d con velocidad v_∞, algo mayor, debido al fuerza que ejerce el campo eléctrico. Después de chocar con la placa negativa, pierde la velocidad que había ganado, u_∞= ε·v_∞. Las ecuaciones son

${\displaystyle \begin{array}{l}d=\frac{u_{\infty }}{\omega }\sin (\omega t)-\left(d+\delta \right)\cos (\omega t)+\delta \\ v_{\infty }=u_{\infty }\cos (\omega t)+\omega \left(d+\delta \right)\sin (\omega t)\\ u_{\infty }=\epsilon v_{\infty }\end{array}}$

Despejamos el tiempo t que tarda la bolita en desplazarse desde la placa positiva a la negativa, que será medio periodo P

${\displaystyle \cos (\omega t)=\frac{\delta (1+\epsilon )-d(1-\epsilon )}{\delta (1+\epsilon )+d(1-\epsilon )}}$

Calculamos también la velocidad u_∞

${\displaystyle u_{\infty }=\frac{\epsilon \omega (d+\delta )\sin (\omega t)}{1-\epsilon \cos (\omega t)}}$

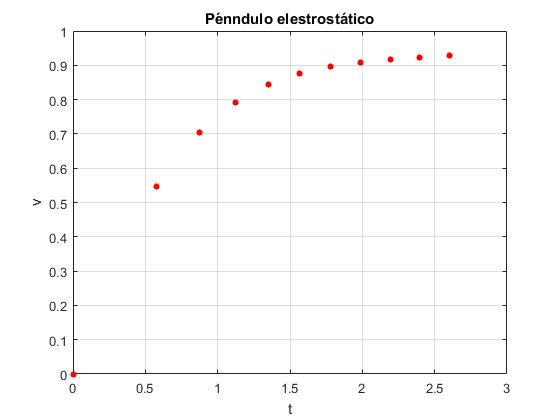
Representamos la velocidad inicial u_n de la bolita cuando sale de la placa positiva en función del tiempo. Vemos que la velocidad tiende hacia un límite constante u_∞. La distancia horizontal entre dos puntos rojos consecutivos es el periodo, que toma un valor constante P

d=0.05; %mitad de la separación entre placas
e=0.9; %coeficente de restituación
ddp=250000; %fem de la batería
w=sqrt(9.8); % el péndulo tiene una longitud de  1 m.

delta=(ddp/(2*d))^2/(4*pi*9e9*2700*0.02*w^2);
N=10; %periodos
v0=0;
P=0;
for i=1:N
    t1=(asin((d-delta)/sqrt((v0/w)^2+(d+delta)^2))
+atan((d+delta)/(v0/w)))/w; 
    v1=v0*cos(w*t1)+w*(d+delta)*sin(w*t1);
    P=P+t1;

    v0=-e*v1;
    t2=(asin((d-delta)/sqrt((v0/w)^2+(d+delta)^2))+
atan((d+delta)/(-v0/w)))/w;
    v2=v0*cos(w*t2)-w*(d+delta)*sin(w*t2);
    P=P+t2;
    v0=-e*v2;
    v(i)=v0;
    tt(i)=P;
end
plot([0,tt],[0,v],'o','markersize',4,'markeredgecolor',
'r','markerfacecolor','r')
grid on
xlabel('t')
ylabel('v')
title('Péndulo elestrostático')

P=2*acos((delta*(1+e)-d*(1-e))/(delta*(1+e)+d*(1-e)))/w
u_inf=e*w*(d+delta)*sin(w*P/2)/(1-e*cos(w*P/2))

P =    0.2012
u_inf =    0.9341

Actividades

Se introduce

• El coeficiente de restitución, e, en el control titulado Coef. restitución

• La diferencia de potencial entre las placas, V, en el control titulado d.d.p.

Se representa la velocidad u_n en función del tiempo t. Vemos que la velocidad final tiene hacia un valor límite constante u_∞. Esta velocidad es proporcional a la diferencia de potencial V₀ entre las placas del condensador

Referencias

Amin Rezaeizadeh, Pooya Mameghani.Thermodynamic model for bouncing charged particles inside a capacitor. Am. J. Phys. 81 (8) August 2013, pp. 632-635

Matej Forjan, Marko Marhl, Vladimir Grubelnik. Mathematical modelling of the electrostatic pendulum in school and undergarduate education. Eur. J. Phys. 35 (2014) 015922

Kazutoshi Asano. On the theory of an electrostatic pendulum oscillator. Am. J. Phys. 43 (5) May 1975, pp. 423-427