Consideremos el circuito de la figura, formado por una batería V₀, dos condensadores C iguales y tres resistencias R iguales. Se cierra el interruptor. En la parte derecha de la figura, se dibujan las intensidades y las cargas de cada uno de los condensadores que calcularemos resolviendo las ecuaciones el circuito

${\displaystyle \begin{array}{l}\{\begin{array}{l}{V}_{ab}+V_{be}+V_{ea}=\mathrm{0,}-V_0+\frac{q_1}{C}+i_{4}R=0(1)\\ V_{ab}+V_{bc}+V_{ca}=\mathrm{0,}-V_0+i_{2}R+\frac{q_2}{C}=0(2)\\ V_{ab}+V_{bc}+V_{cd}+V_{da}=\mathrm{0,}-V_0+i_{2}R-i_{3}R+i_{4}R=0(3)\end{array}\\ \{\begin{array}{l}{i}_5=i_2+i_3(4)\\ i_1=i_4+i_3(5)\end{array}\\ \{\begin{array}{l}{i}_1=\frac{d{q}_1}{dt}(6)\\ i_5=\frac{d{q}_2}{dt}(7)\end{array}\end{array}}$

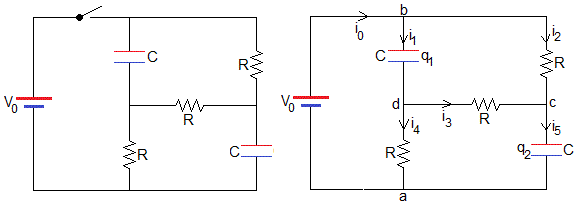
Las intensidades i₁ e i₅ añaden carga a los respectivos condensadores. Por tanto, i₁=dq₁/dt y lo mismo para el otro condensador

Tenemos que resolver un sistema de siete ecuaciones con siete incógnitas. Para resolver las ecuaciones diferenciales, precisamos conocer las cargas e intensidades iniciales en el instante t=0

Condiciones iniciales

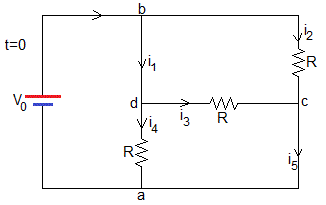
En el instante t=0, las cargas q₁ y q₂ de los condensadores son nulas, la diferencia de potencial V_bd=0 y V_ca=0. En la figura se muestra el circuito equivalente

Las ecuaciones del circuito son

${\displaystyle \begin{array}{l}\{\begin{array}{l}{V}_{ab}+V_{ba}=\mathrm{0,}-V_0+i_{4}R=0\\ V_{ab}+V_{bc}=\mathrm{0,}-V_0+i_{2}R=0\\ V_{ab}+V_{bc}+V_{cd}+V_{da}=\mathrm{0,}-V_0+i_{2}R-i_{3}R+i_{4}R=0\end{array}\\ i_3(0)=\frac{V_0}{R},i_2(0)=\frac{V_0}{R},i_4(0)=\frac{V_0}{R}\end{array}}$

De las ecuaciones (4) y (5) obtenemos

${\displaystyle i_1(0)=2\frac{V_0}{R},i_5(0)=2\frac{V_0}{R}}$

Sistema de ecuaciones

Los pasos para resolver el sistema de siete ecuaciones son los siguientes

• Derivamos (1) y (2)

${\displaystyle \{\begin{array}{l}\frac{1}{C}\frac{d{q}_1}{dt}+\frac{d{i}_4}{dt}R=\mathrm{0,}\frac{i_1}{C}+\frac{d{i}_4}{dt}R=0(8)\\ \frac{d{i}_2}{dt}R+\frac{1}{C}\frac{d{q}_2}{dt}=\mathrm{0,}\frac{d{i}_2}{dt}R+\frac{i_5}{C}=0(9)\end{array}}$

• Sumamos (4) y (5)

${\displaystyle i_1+i_5=i_2+2i_3+i_4(10)}$

• Sumamos (8) y (9) y con el resultado (10)

${\displaystyle \begin{array}{l}\frac{i_1+i_5}{C}+\frac{d\left(i_4+i_2\right)}{dt}R=0\\ \frac{i_2+2i_3+i_4}{C}+\frac{d\left(i_4+i_2\right)}{dt}R=0(11)\end{array}}$

• De la ecuación (3)

${\displaystyle i_2+i_4=\frac{V_0}{R}+i_3(12)}$

• Sustituimos (12) en (11) y obtenemos una ecuación diferencial

${\displaystyle \begin{array}{l}\frac{\frac{V_0}{R}+3i_3}{C}+\frac{d\left(\frac{V_0}{R}+i_3\right)}{dt}R=0\\ \frac{d{i}_3}{dt}+\frac{3}{RC}{i}_3=-\frac{V_0}{R^{2}C}\end{array}}$

Intensidades

• i₃

Resolvemos la ecuación diferencial en i₃

La solución particular de esta ecuación diferencial es la constante k tal que

${\displaystyle \frac{3}{RC}k=-\frac{V_0}{R^{2}C},k=-\frac{V_0}{3R}}$

La solución de la ecuación diferencial homogénea es

${\displaystyle A\exp \left(-\frac{3}{RC}t\right)}$

La solución completa es

${\displaystyle i_3=-\frac{V_0}{3R}+A\exp \left(-\frac{3}{RC}t\right)}$

El coeficiente A se determina a partir de las condiciones iniciales, i₃(0)

${\displaystyle i_3(0)=-\frac{V_0}{3R}+A=\frac{V_0}{R},A=\frac{4V_0}{3R}}$

La intensidad i₃ varía en función del tiempo t de la forma

${\displaystyle i_3=\frac{1}{3}\frac{V_0}{R}\left(-1+4\exp \left(-\frac{3}{RC}t\right)\right)}$

• i₂

De las ecuaciones (9) y (4) obtenemos una ecuación diferencial de i₂

${\displaystyle \begin{array}{l}R\frac{d{i}_2}{dt}+\frac{i_2+i_3}{C}=0\\ \frac{d{i}_2}{dt}+\frac{i_2}{RC}=-\frac{1}{3}\frac{V_0}{R^{2}C}\left(-1+4\exp \left(-\frac{3}{RC}t\right)\right)\end{array}}$

La solución particular es de la forma

${\displaystyle a+b\exp \left(-\frac{3}{RC}t\right)}$

La introducimos en la ecuación diferencial y obtenemos

${\displaystyle a=\frac{1}{3}\frac{V_0}{R},b=\frac{2}{3}\frac{V_0}{R}}$

La solución de la ecuación diferencial homogénea es

${\displaystyle A\exp \left(-\frac{1}{RC}t\right)}$

La solución completa es

${\displaystyle i_2=\frac{1}{3}\frac{V_0}{R}+\frac{2}{3}\frac{V_0}{R}\exp \left(-\frac{3}{RC}t\right)+A\exp \left(-\frac{1}{RC}t\right)}$

La intensidad inicial i₂(0) determina el coeficiente A

${\displaystyle i_2(0)=\frac{1}{3}\frac{V_0}{R}+\frac{2}{3}\frac{V_0}{R}+A=\frac{V_0}{R},A=0}$

La intensidad i₂ varía en función del tiempo t de la forma

${\displaystyle i_2=\frac{1}{3}\frac{V_0}{R}\left(1+2\exp \left(-\frac{3}{RC}t\right)\right)}$

• i₄

De la ecuación (12)

${\displaystyle i_2+i_4=\frac{V_0}{R}+i_3=\frac{V_0}{3R}\left(2+4\exp \left(-\frac{3}{RC}t\right)\right)}$

Conocido i₂, despejamos i₄

${\displaystyle i_4=\frac{1}{3}\frac{V_0}{R}\left(1+2\exp \left(-\frac{3}{RC}t\right)\right)}$

Las intensidades i₂ e i₄ son iguales

• i₅

De la ecuación (4)

${\displaystyle i_5=i_2+i_3=2\frac{V_0}{R}\exp \left(-\frac{3}{RC}t\right)}$

• i₁

De la ecuación (5)

${\displaystyle i_1=i_4+i_3=2\frac{V_0}{R}\exp \left(-\frac{3}{RC}t\right)}$

Las intensidades i₁ e i₅ son iguales

Representamos las intensidades en unidades V₀/R en función del tiempo adimensional t/(RC)

i3=@(x) (-1+4*exp(-3*x))/3;
hold on
fplot(i3,[0,3])
i2=@(x) (1+2*exp(-3*x))/3; %igual a i4
fplot(i2,[0,3])
i1=@(x) 2*exp(-3*x);%igual a i5
fplot(i1,[0,3])
hold off
xlabel('t/(RC)')
ylabel('i/(V_0/R)')
legend('i_3','i_2=i_4','i_1=i_5','Location','best')
grid on
title('Intensidades')

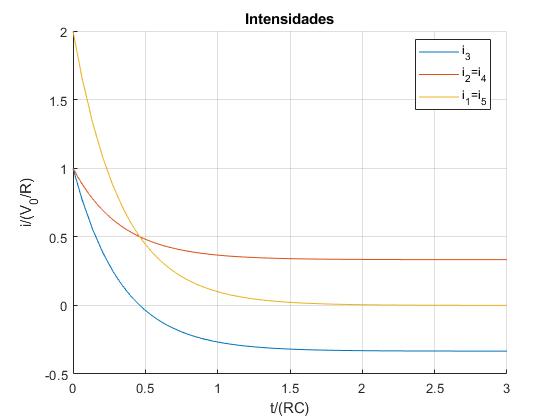
• Las intensidades i₁ e i₅, tienden a cero cuando t→∞

• Las intensidades i₂ e i₄, tienden a V₀/(3R) cuando t→∞

• La intensidad i₃ se anula en el instante t

${\displaystyle -1+4\exp \left(-\frac{3}{RC}t\right)=\mathrm{0,}t=\frac{\ln 4}{3}RC}$

Luego, tiende hacia el valor constante -V₀/(3R) cuando t→∞

Cargas de los condensadores

Los condensadores están inicialmente descargados, q₁(0)=0, q₂(0)=0

• q₁

De la ecuación (6)

${\displaystyle \begin{array}{l}{i}_1=\frac{d{q}_1}{dt}\\ \frac{d{q}_1}{dt}=2\frac{V_0}{R}\exp \left(-\frac{3}{RC}t\right)\\ q_1=2\frac{V_0}{R}{\displaystyle \underset{0}{\overset{t}{\int }}\exp \left(-\frac{3}{RC}t\right)dt}\\ q_1=\frac{2}{3}{V}_{0}C\left(1-\exp \left(-\frac{3}{RC}t\right)\right)\end{array}}$

• q₂

De la ecuación (7)

${\displaystyle i_5=\frac{d{q}_2}{dt}}$

Como i₁ es igual a i₅, la carga q₁ es la misma que la carga q₂

${\displaystyle q_2=\frac{2}{3}{V}_{0}C\left(1-\exp \left(-\frac{3}{RC}t\right)\right)}$

Representamos las cargas q₁, q₂ en unidades V₀C en función del tiempo adimensional t/(RC)

q=@(x) 2*(1-exp(-3*x))/3;
fplot(q,[0,3])
xlabel('t/(RC)')
ylabel('q/(V_0·C)')
grid on
title('Cargas')

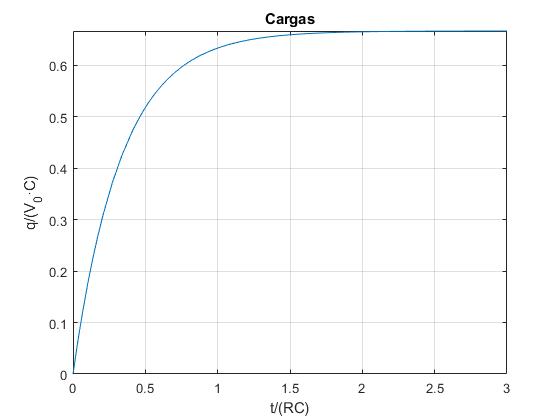
Las cargas q₁ y q₂ tienden hacia el valor constante 2V₀C/3, que es la carga máxima, cuando t→∞

Energías

• Energía suministrada por la batería

La corriente que pasa por la batería es i₀=i₁+i₂

${\displaystyle i_0=2\frac{V_0}{R}\exp \left(-\frac{3}{RC}t\right)+\frac{1}{3}\frac{V_0}{R}+\frac{2}{3}\frac{V_0}{R}\exp \left(-\frac{3}{RC}t\right)=\frac{1}{3}\frac{V_0}{R}\left(1+8\exp \left(-\frac{3}{RC}t\right)\right)}$

La energía suministrada por la batería hasta el instante t es

${\displaystyle E_B={\displaystyle \underset{0}{\overset{t}{\int }}{V}_0{i}_{0}dt=}\frac{1}{3}\frac{V_0^2}{R}{\displaystyle \underset{0}{\overset{t}{\int }}\left(1+8\exp \left(-\frac{3}{RC}t\right)\right)dt}=\frac{1}{3}\frac{V_0^2}{R}\left\{t+\frac{8}{3}RC\left(1-\exp \left(-\frac{3}{RC}t\right)\right)\right\}}$

• Energía disipada en la resistencia

${\displaystyle \begin{array}{l}{E}_R={\displaystyle \underset{0}{\overset{t}{\int }}\left(i_4^{2}R+i_2^{2}R+i_3^{2}R\right)}dt={\displaystyle \underset{0}{\overset{t}{\int }}\left(2i_4^{2}R+i_3^{2}R\right)}dt\\ =\frac{1}{9}\frac{V_0^2}{R}{\displaystyle \underset{0}{\overset{t}{\int }}\left\{2{\left(1+2\exp \left(-\frac{3}{RC}t\right)\right)}^2+{\left(-1+4\exp \left(-\frac{3}{RC}t\right)\right)}^2\right\}}dt=\\ \frac{1}{9}\frac{V_0^2}{R}{\displaystyle \underset{0}{\overset{t}{\int }}\left\{3+24\exp \left(-\frac{6}{RC}t\right)\right\}}dt=\frac{1}{9}\frac{V_0^2}{R}\left\{3t+4RC\left(1-\exp \left(-\frac{6}{RC}t\right)\right)\right\}\end{array}}$

• Energía acumulada en los condensadores

${\displaystyle E_C=\frac{1}{2}\frac{q_1^2}{C}+\frac{1}{2}\frac{q_2^2}{C}=\frac{q_1^2}{C}=\frac{4}{9}{V}_0^{2}C{\left(1-\exp \left(-\frac{3}{RC}t\right)\right)}^2}$

Comprobamos que E_C+E_R=E_B. Una parte de la energía suministrada por la batería, se acumula en forma de campo eléctrico en los dos condensadores, el resto, se disipa en las tres resistencias.

Representamos las energías en unidades V₀²C en función del tiempo adimensional t/(RC)

eB=@(x) (x+8*(1-exp(-3*x))/3)/3;
eC=@(x) 4*(1-exp(-3*x)).^2/9;
eR=@(x) (3*x+4*(1-exp(-6*x)))/9;
hold on
fplot(eB,[0,3])
fplot(eC,[0,3])
fplot(eR,[0,3])
% f=@(x) eC(x)+eR(x);
% fplot(f,[0,3],'color','k')
hold off
xlabel('t/(RC)')
ylabel('E/(V_0^2·C)')
legend('E_B','E_C','E_R','Location','best')
grid on
title('Energías')

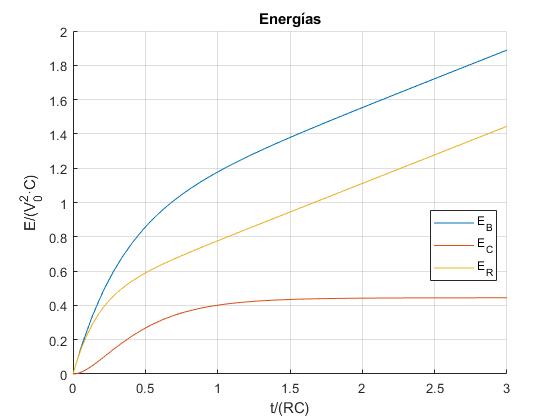
La energía de los condensadores tiende hacia el valor máximo, cuando t→∞

${\displaystyle 2\left(\frac{1}{2}\frac{{\left(\frac{2}{3}{V}_{0}C\right)}^2}{C}\right)=\frac{4}{9}{V}_0^{2}C}$

La carga máxima de cada condensador está entre paréntesis en el numerador

Una vez alcanzado el estado estacionario (t→∞), la energía de la batería se disipa en la resistencia

Referencias

Physics Challenge for Teachers and Students. A trip aCRoss the Bridge. The Physics Teacher. Vol. 53, May 2015. pp. 316