Dispersión por un potencial repulsivo V(r)=k/r²

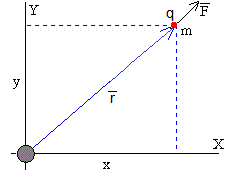
La energía E y el momento angular L en coordenadas polares de una partícula de masa m y carga q son

${\displaystyle \begin{array}{l}E=\frac{1}{2}m{\left(\frac{dr}{dt}\right)}^2+\frac{1}{2}m{r}^2{\left(\frac{d\theta }{dt}\right)}^2+qV(r)\\ L=m{r}^2\frac{d\theta }{dt}\end{array}}$

Estas dos magnitudes son constantes en todos los puntos de la trayectoria e iguales a su valor inicial

${\displaystyle \begin{array}{l}L=m{v}_{0}b\\ E=\frac{1}{2}m{v}_0^2\end{array}}$

b se denomina parámetro de impacto y v₀ es la velocidad de la partícula en el infinito. La ecuación diferencial de la trayectoria es

${\displaystyle \begin{array}{l}\begin{array}{l}E=\frac{1}{2}m{\left(\frac{dr}{dt}\right)}^2+\frac{L^2}{2m{r}^2}+qV(r)\hfill \\ \{\begin{array}{l}\frac{d\theta }{dt}=\frac{L}{m{r}^2}\\ \frac{dr}{dt}=\sqrt{\frac{2}{m}\left(E-\frac{L^2}{2m{r}^2}-qV(r)\right)}\end{array}\hfill \end{array}\\ \frac{d\theta }{dr}=\frac{\frac{L}{m{r}^2}}{\sqrt{\frac{2}{m}\left(E-\frac{L^2}{2m{r}^2}-qV(r)\right)}}\end{array}}$

Sustituimos E, L y V(r)

${\displaystyle \begin{array}{l}\frac{d\theta }{dr}=\frac{\frac{m{v}_{0}b}{m{r}^2}}{\sqrt{\frac{2}{m}\left(\frac{1}{2}m{v}_0^2-\frac{m^2{v}_0^2{b}^2}{2m{r}^2}-q\frac{Q}{4\pi {\epsilon }_0{r}^2}\right)}}\hfill \\ d\theta =\frac{\frac{b}{r^2}}{\sqrt{\left(1-\frac{b^2}{r^2}-\frac{qQ}{2\pi {\epsilon }_{0}m{v}_0^2}\frac{1}{r^2}\right)}}dr\hfill \end{array}}$

Hacemos el cambio de variable u=1/r, du=-dr/r²

${\displaystyle d\theta =\frac{-bdu}{\sqrt{1-k^2{u}^2}}=-\frac{b}{k}\frac{du}{\sqrt{\frac{1}{k^2}-u^2}},k^2=b^2+\frac{qQ}{2\pi {\epsilon }_{0}m{v}_0^2}}$

La ecuación de la trayectoria en coordenadas polares es

${\displaystyle \begin{array}{l}\theta =-\frac{b}{k}\arcsin \left(\frac{u}{\frac{1}{k}}\right)+C\\ c-\frac{k}{b}\theta =\arcsin \left(\frac{k}{r}\right)\\ r=\frac{k}{\sin \left(c-\frac{k}{b}\theta \right)}\end{array}}$

La constante c se determina sabiendo que la partícula parte del infinito, r→∞ con un parámetro de impacto b, la posición angular θ→0 (véase la figura más abajo). Por tanto, c=π. La ecuacion de la trayectoria en coordenadas polares es

${\displaystyle r=\frac{k}{\sin \left(\pi -\frac{k}{b}\theta \right)}}$

La otra asíntota se obtiene para el ángulo θ₁ tal que π-kθ₁/b=0, es decir, cuando r→∞

El ángulo de dispersión es

${\displaystyle \Phi =\pi -{\theta }_1=\pi -\frac{b}{k}\pi =\left(1-\frac{b}{k}\right)\pi }$

En la posición de mínima distancia se cumple que la componente radial de la velocidad es nula, dr/dt=0

Para un parámetro de impacto dado b, la distancia mínima r_m entre la partícula y el centro fijo de fuerzas es

${\displaystyle \begin{array}{l}E=\frac{L^2}{2m{r}_m^2}+\frac{Qq}{4\pi {\epsilon }_0{r}_m^2}\hfill \\ \frac{1}{2}m{v}_0^2=\frac{m^2{v}_0^2{b}^2}{2m{r}_m^2}+\frac{Qq}{4\pi {\epsilon }_0{r}_m^2}\hfill \\ r_m^2=b^2+\frac{Qq}{2\pi {\epsilon }_{0}m{v}_0^2}\hfill \\ r_m=k\hfill \end{array}}$

Cuando el parámero de impacto b=0, la partícula se mueve hacia el centro de fuerzas hasta una distancia h y luego, retrocede

${\displaystyle \begin{array}{l}\frac{1}{2}m{v}_0^2=\frac{Qq}{4\pi {\epsilon }_0{h}^2}\hfill \\ h^2=\frac{Qq}{2\pi {\epsilon }_{0}m{v}_0^2}\hfill \\ r_m^2=b^2+h^2\hfill \end{array}}$

La ecuación de la trayectoria en términos de los parámetros r_m y h se escribe

${\displaystyle r=\frac{r_m}{\sin \left(\pi -\frac{r_m}{\sqrt{r_m^2-h^2}}\theta \right)}=\frac{r_m}{\sin \left(\pi -\frac{\theta }{\sqrt{1-\frac{h^2}{r_m^2}}}\right)}}$

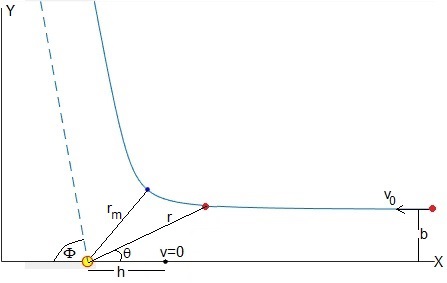
Para representar la trayectoria se ha empleado el código MATLAB

h2=0.2; %se fija la energía de la partícula
hold on
b=0.3; % parámetro de impacto
k2=b^2+h2;
r=@(x) sqrt(k2)./sin(pi-sqrt(k2)*x/b);
Th=pi*b/sqrt(k2); %asíntota
fplot(@(x) r(x).*cos(x),@(x) r(x).*sin(x),[0.05,Th-0.05])
plot(0,0,'ro', 'markersize',8,'markerfacecolor','y')
plot(sqrt(k2)*cos(Th/2),sqrt(k2)*sin(Th/2),'bo', 'markersize',3
,'markerfacecolor','b')
plot(sqrt(h2),0,'ko', 'markersize',3,'markerfacecolor','k')
line([0,-0.5],[0,0.5*tan(pi-Th)],'lineStyle','--') %asíntota
hold off
axis equal
xlim([-0.5,2])
ylim([0,1.5])
xlabel('x')
ylabel('y')
title('Dispersión')

Representamos las trayectorias para una energía fijada por el parámetro h², para varios parámeros de imapacto b

h2=0.2; %se fija la energía de la partícula
hold on
for b=0.1:0.1:1 % parámetro de impacto
    k2=b^2+h2;
    r=@(x) sqrt(k2)./sin(pi-sqrt(k2)*x/b);
    fplot(@(x) r(x).*cos(x),@(x) r(x).*sin(x),[0.05, pi*b/sqrt(k2)-0.05])
    %simétrica
    fplot(@(x) r(x).*cos(x),@(x) -r(x).*sin(x),[0.05, pi*b/sqrt(k2)-0.05])
end
plot(0,0,'ro', 'markersize',8,'markerfacecolor','y') %centro de fuerzas
hold off
grid on
axis equal
xlim([-2,2])
ylim([-1.5,1.5])
xlabel('x')
ylabel('y')
title('Dispersión')

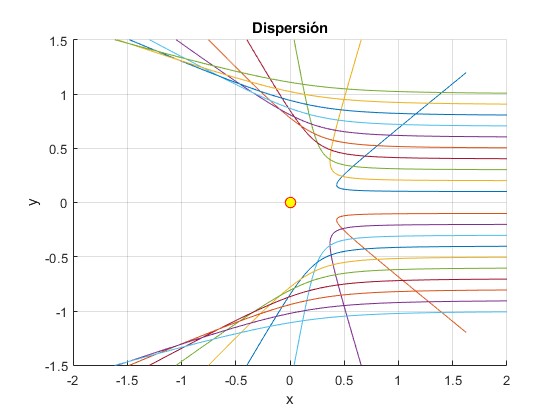
Envolvente

La ecuación de la trayectoria depende del parámetro de impacto b, f(r, θ, b)=0

${\displaystyle r\sin \left(\pi -\frac{\sqrt{b^2+h^2}}{b}\theta \right)-\sqrt{b^2+h^2}=0}$

La ecuación de la envolvente de las trayectorias se obtiene derivando con respecto a b e igualando a cero.

${\displaystyle \begin{array}{l}\frac{\partial f}{\partial b}=0\\ r\left(-\frac{\frac{b^2}{\sqrt{b^2+h^2}}-\sqrt{b^2+h^2}}{b^2}\right)\cos \left(\pi -\frac{\sqrt{b^2+h^2}}{b}\theta \right)-\frac{b}{\sqrt{b^2+h^2}}=0\\ r\frac{h^2}{b^2}\cos \left(\pi -\frac{\sqrt{b^2+h^2}}{b}\theta \right)-b=0\end{array}}$

No podemos despejar b de la ecuación de la trayectoria y sustituirlo en esta última. La ecuación de la envolvente viene descrita por el sistema de dos ecuaciones

${\displaystyle \{\begin{array}{l}r\sin \left(\pi -\frac{\sqrt{b^2+h^2}}{b}\theta \right)-\sqrt{b^2+h^2}=0\\ r{h}^2\cos \left(\pi -\frac{\sqrt{b^2+h^2}}{b}\theta \right)-b^3=0\end{array}}$

Dado el parámetro b, se resuelve el sistema de dos ecuaciones no lineales mediante fsolve para obtener r y θ que representa un punto, en coordenadas polares, de la envolvente (curva de color rojo)

h2=0.8; %se fija la energía de la partícula
hold on
for b=0.1:0.1:1 % parámetro de impacto
    k2=b^2+h2;
    r=@(x) sqrt(k2)./sin(pi-sqrt(k2)*x/b);
    fplot(@(x) r(x).*cos(x),@(x) r(x).*sin(x),[0.05, pi*b/sqrt(k2)-0.05])
    fplot(@(x) r(x).*cos(x),@(x) -r(x).*sin(x),[0.05, pi*b/sqrt(k2)-0.05])
end
plot(0,0,'ro', 'markersize',8,'markerfacecolor','y')
%envolvente
bb=0.1:0.05:1;
z=zeros(length(bb),2);
j=1;
for b=bb
%r es x(1) y th es x(2)
    k2=b^2+h2;
    F=@(x) [x(1)*sin(pi-sqrt(k2)*x(2)./b)-sqrt(k2); x(1)*h2*
cos(pi-sqrt(k2)*x(2)./b)-b.^3];
    zz=fsolve(F,[sqrt(k2),pi*b/(2*sqrt(k2))]);
        z(j,1)=zz(1);
        z(j,2)=zz(2);
        j=j+1;
end
plot(z(:,1).*cos(z(:,2)),z(:,1).*sin(z(:,2)),'r')
plot(z(:,1).*cos(z(:,2)),-z(:,1).*sin(z(:,2)),'r')
hold off
grid on
axis equal
xlim([-2,2])
ylim([-1.5,1.5])
xlabel('x')
ylabel('y')
title('Dispersión')

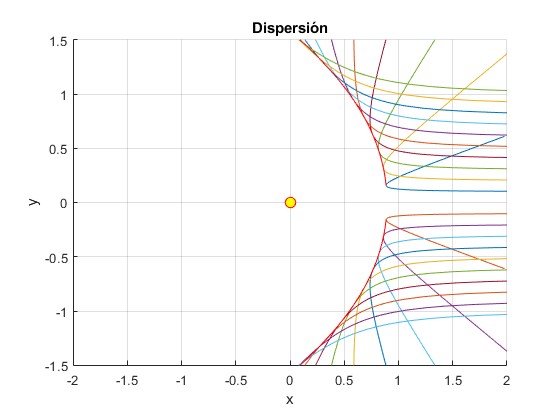
Para h²=0.2, el error en la envolvente es importante para valores del parámetro de impacto b grandes

Alternativamente, utilizamos el procedimiento de Newton-Raphson, para representar la evolvente, para ello necesitamos determinar la matriz J del siguiente modo

${\displaystyle \begin{array}{l}\{\begin{array}{l}f\left(r,\theta \right)=r\sin \left(\pi -\frac{\sqrt{b^2+h^2}}{b}\theta \right)-\sqrt{b^2+h^2}=0\\ g\left(r,\theta \right)=r{h}^2\cos \left(\pi -\frac{\sqrt{b^2+h^2}}{b}\theta \right)-b^3=0\end{array}\\ J=\left(\begin{array}{cc}\frac{\partial f}{\partial r}& \frac{\partial f}{\partial \theta }\\ \frac{\partial g}{\partial r}& \frac{\partial g}{\partial \theta }\end{array}\right)=\left(\begin{array}{cc}\sin \left(\pi -\frac{\sqrt{b^2+h^2}}{b}\theta \right)& -\frac{\sqrt{b^2+h^2}}{b}r\cos \left(\pi -\frac{\sqrt{b^2+h^2}}{b}\theta \right)\\ h^2\cos \left(\pi -\frac{\sqrt{b^2+h^2}}{b}\theta \right)& \frac{\sqrt{b^2+h^2}}{b}r{h}^2\sin \left(\pi -\frac{\sqrt{b^2+h^2}}{b}\theta \right)\end{array}\right)\end{array}}$

function hiperbola_8
    h2=0.8; %se fija la energía de la partícula
    hold on
    for b=0.1:0.05:1 % parámetro de impacto
        k2=b^2+h2;
        r=@(x) sqrt(k2)./sin(pi-sqrt(k2)*x/b);
        fplot(@(x) r(x).*cos(x),@(x) r(x).*sin(x),[0.05, pi*b/sqrt(k2)-0.05])
        fplot(@(x) r(x).*cos(x),@(x) -r(x).*sin(x),[0.05, pi*b/sqrt(k2)-0.05])
    end
    plot(0,0,'ro', 'markersize',8,'markerfacecolor','y')
%envolvente
    bb=0.1:0.05:1;
     z=zeros(length(bb),2);
     j=1;
    for b=bb
        zz=envolvente(b);
        z(j,1)=zz(1);
        z(j,2)=zz(2);
        %disp([zz(1),zz(2)])
        j=j+1;
     end
    plot(z(:,1).*cos(z(:,2)),z(:,1).*sin(z(:,2)),'r')
    hold off
    grid on
    axis equal
    xlim([-2,2])
    ylim([-1.5,1.5])
    xlabel('x')
    ylabel('y')
    title('Dispersión')

    function x=envolvente(b)
        k2=b^2+h2;
        F=@(x) [x(1)*sin(pi-sqrt(k2)*x(2)./b)-sqrt(k2); 
x(1)*h2*cos(pi-sqrt(k2)*x(2)./b)-b.^3];
        J=@(x) [sin(pi-sqrt(k2)*x(2)./b), -x(1)*sqrt(k2)*cos(pi-sqrt(k2)*x(2)./b)/b
; h2*cos(pi-sqrt(k2)*x(2)./b), x(1)*h2*sin(pi-sqrt(k2)*x(2)./b)*sqrt(k2)/b];
        x=[sqrt(k2),pi*b/(2*sqrt(k2))]; %valor inicial
        for i=1:100
            dx=-J(x)\F(x);
            if sqrt(norm(dx)/norm(x))<0.001
%                   disp(x+dx)
                break;
            end
            x=x+dx;
        end
        if i==100
            disp('Se ha soprepasado el número de iteracciones');
        end
    end
end

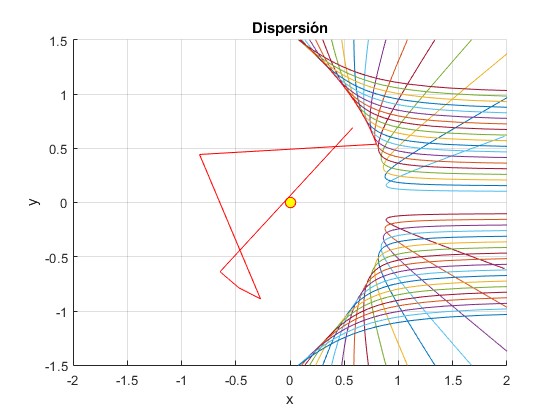
Para los primeros valores del parámetro de impacto b, el procedimiento no realiza bien los cálculos tal como se puede ver en la siguiente tabla

La primera columna b es el parámetro de impacto. La segunda y tercera columna, es la posición (r,θ) de un punto de la envolvente en coordendas polares, calculado mediante fsolve de MATLAB. La cuarta y quinta columna es la posición de dicho punto calculada medinte el método de Newton-Raphson

A partir de b=0.4 ambos procedimientos coinciden en los resultados

Dispersión de un ión por un átomo neutro

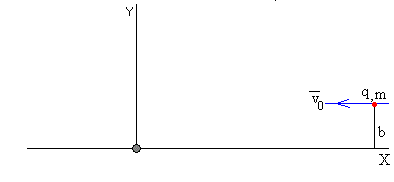
Consideremos un átomo inmóvil, situado en el origen y un ión de msa m y carga q situado a una distancia r

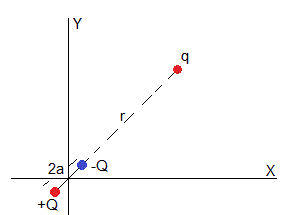
El campo eléctrico producido por el ión polariza el átomo que podemos considerar ahora como un dipolo de cargas +Q y -Q separadas una distancia 2a.

El campo eléctrico producido por el dipolo en la posición del ión es

${\displaystyle E_p=\frac{1}{4\pi {\epsilon }_0}\frac{Q}{{(r+a)}^2}-\frac{1}{4\pi {\epsilon }_0}\frac{Q}{{(r-a)}^2}=\frac{Q}{4\pi {\epsilon }_0{r}^2}\left({\left(1+\frac{a}{r}\right)}^{-2}-{\left(1-\frac{a}{r}\right)}^{-2}\right)}$

Como a<<r, aproximamos a

${\displaystyle E_p\approx \frac{Q}{4\pi {\epsilon }_0{r}^2}\left(\left(1-\frac{2a}{r}\right)-\left(1+\frac{2a}{r}\right)\right)=-\frac{4Qa}{4\pi {\epsilon }_0{r}^3}}$

El campo eléctrico E_i producido por el ión polariza el átomo, p=α·E_i, donde p es el momento dipolar p=Q(2a). Calculamos la carga Q del dipolo

${\displaystyle \begin{array}{l}p=\alpha \frac{1}{4\pi {\epsilon }_0}\frac{q}{r^2}\\ Q=\frac{\alpha }{2a}\frac{1}{4\pi {\epsilon }_0}\frac{q}{r^2}\end{array}}$

El campo producido por el átomo neutro situado en el origen, en la posición del ión es

${\displaystyle E_p=-\frac{2\alpha }{{\left(4\pi {\epsilon }_0\right)}^2}\frac{q}{r^5}}$

La fuerza sobre el ión es atractiva

${\displaystyle f_p=-\frac{2\alpha }{{\left(4\pi {\epsilon }_0\right)}^2}\frac{q^2}{r^5}}$

El potencial V(r) correspondiente al campo E_p es

${\displaystyle V(r)={\displaystyle \underset{r}{\overset{\infty }{\int }}-\frac{2\alpha }{{\left(4\pi {\epsilon }_0\right)}^2}\frac{q}{r^5}dr=}-\frac{\alpha }{2{\left(4\pi {\epsilon }_0\right)}^2}\frac{q}{r^4}}$

En la posición de mínima distancia se cumple que la componente radial de la velocidad es nula, dr/dt=0. Dicha posición r_m es la raíz real positiva de la ecuación bicuadrada

${\displaystyle \begin{array}{l}E=\frac{1}{2}m{\left(\frac{dr}{dt}\right)}^2+\frac{L^2}{2m{r}^2}+qV(r),\{\begin{array}{l}L=bm{v}_0\\ E=\frac{1}{2}m{v}_0^2\end{array}\hfill \\ E=\frac{m^2{b}^2\frac{2E}{m}}{2m{r}_m^2}-\frac{\alpha }{2{(4\pi {\epsilon }_0)}^2}\frac{q^2}{r_m^4}\hfill \\ r_m^2-b^2+\frac{k}{r_m^{2}E}=\mathrm{0,}k=\frac{\alpha q^2}{2{(4\pi {\epsilon }_0)}^2}\hfill \end{array}}$

Las raíces reales se obtienen siempre que

${\displaystyle b^4\ge 4\frac{k}{E}\text{,}b\ge {\left(\frac{\alpha q^2}{4{\left(\pi {\epsilon }_0\right)}^{2}m{v}_0^2}\right)}^{1/4}}$

Trayectorias

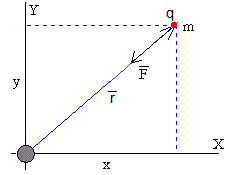
Las ecuaciones del movimiento del ión de masa m son

${\displaystyle \begin{array}{l}m\frac{d^{2}x}{d{t}^2}=-\frac{4k}{r^5}\frac{x}{r}\\ m\frac{d^{2}y}{d{t}^2}=-\frac{4k}{r^5}\frac{y}{r}\end{array}}$

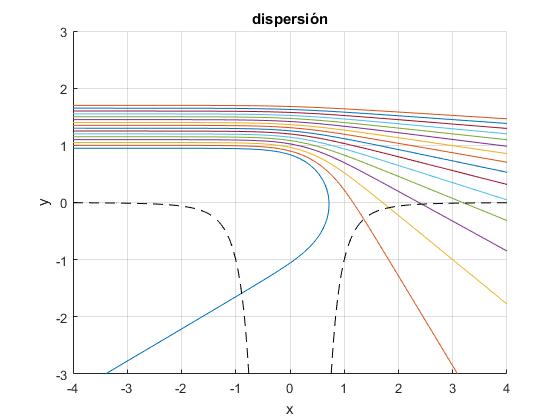
Representamos las trayectorias seguidas por los iones, resolviendo el sistema de ecuaciones diferenciales por procedimientos numéricos. Superponemos en líneas a trazos, la curva de energía potencial E_p(r)=-k/r⁴

k=1;
energia=5;
N=20; %partículas
tspan=[0,10];
hold on
potencial=@(r) -k./r.^4;
for i=1:N
    b=0.7+i/N; %parámetro de impacto
    if b>(4*k/energia)^(1/4)
        x0=[-10,sqrt(2*energia),b,0];
        fg=@(t,x)[x(2);-4*k*x(1)/(x(1)^2+x(3)^2)^3; x(4); 
-4*k*x(3)/(x(1)^2+x(3)^2)^3];
        [t,x]=ode45(fg,tspan,x0);
        plot(x(:,1),x(:,3))    
    end
end
fp=fplot(potencial,[0.05,5],'--k');
plot(-fp.XData,fp.YData,'--k')
ylim([-3,3]);
xlim([-4,4])
hold off
grid on
xlabel('x')
ylabel('y');
title('dispersión')

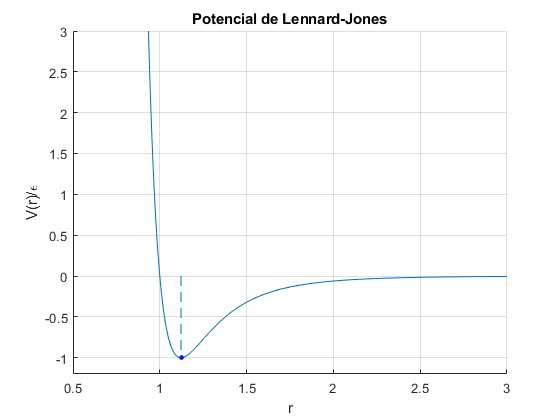
Potencial de Lennard-Jones

Hemos estudiado el potencial de Lennard-Jones en la página titulada Vibración de una molécula diatómica. La expresión equivalente de este potencial es

${\displaystyle V(r)=4\epsilon \left({\left(\frac{\ell }{r}\right)}^{12}-{\left(\frac{\ell }{r}\right)}^6\right)}$

Representamos V(r)/ε en función de r, tomando l=1

Presenta un mínimo para r₀=2^1/6

${\displaystyle \begin{array}{l}\frac{dV}{dr}=4\epsilon \left(-\frac{12}{r}{\left(\frac{\ell }{r}\right)}^{12}+\frac{6}{r}{\left(\frac{\ell }{r}\right)}^6\right)=0\\ -2{\left(\frac{\ell }{r_0}\right)}^{12}+{\left(\frac{\ell }{r_0}\right)}^6=0\\ {\left(\frac{\ell }{r_0}\right)}^6=\frac{1}{2}\\ r_0=2^{\frac{1}{6}}\ell \end{array}}$

g=@(x) 4*(1./x.^12-1./x.^6);
hold on
fplot(g,[0.8,3])
min=2^(1/6); %mínimo
plot(min,g(min),'bo','markersize',3,'markerfacecolor','b')
line([min,min],[0, g(min)],'lineStyle','--')
hold off
grid on
ylim([-1.2,3])
xlabel('r')
ylabel('V(r)/\epsilon')
title('Potencial de Lennard-Jones')

Expresamos el potencial de Lennard-Jones en términos del parámetro r₀

${\displaystyle \begin{array}{l}V(r)=4\epsilon \left(\frac{1}{4}{\left(\frac{r_0}{r}\right)}^{12}-\frac{1}{2}{\left(\frac{r_0}{r}\right)}^6\right)\\ V(r)=\epsilon \left({\left(\frac{r_0}{r}\right)}^{12}-2{\left(\frac{r_0}{r}\right)}^6\right)\end{array}}$

Estudiamos la dispersión de una partícula en el potencial V(r)

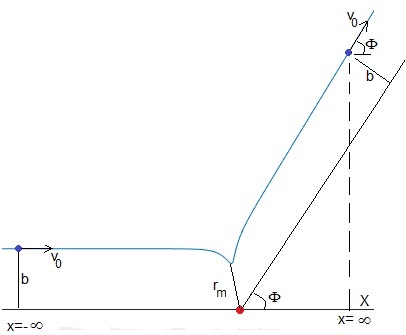
Desde x=-∞, se lanza una partícula de masa m con velocidad v₀ con parámetro de impacto b. La partícula se mueve hacia el centro de fuerzas acercándose a un distancia r_m. Cuando la partícula llega a x=∞, el módulo de su velocidad es v₀ y su dirección hace un ángulo de dispersión Φ.

La energía y el momento angular son constantes

${\displaystyle E=\frac{1}{2}m{\left(\frac{dr}{dt}\right)}^2+\frac{L^2}{2m{r}^2}+V(r),\{\begin{array}{l}E=\frac{1}{2}m{v}_0^2\\ L=bm{v}_0\end{array}}$

La energía potencial efectiva es

${\displaystyle \begin{array}{l}{v}_{ef}(r)=\frac{L^2}{2m{r}^2}+4\epsilon \left({\left(\frac{\ell }{r}\right)}^{12}-{\left(\frac{\ell }{r}\right)}^6\right)\hfill \\ \begin{array}{l}{V}_{ef}(r)=\frac{b^2{m}^2\frac{2E}{m}}{2m{r}^2}+4\epsilon \left({\left(\frac{\ell }{r}\right)}^{12}-{\left(\frac{\ell }{r}\right)}^6\right)\\ V_{ef}(r)=\frac{b^{2}E}{r^2}+4\epsilon \left({\left(\frac{\ell }{r}\right)}^{12}-{\left(\frac{\ell }{r}\right)}^6\right)\end{array}\hfill \end{array}}$

Establecemos un sistema de unidades, tal que l=1, la energía y el potencial V_ef(r) se miden en unidades de ε

${\displaystyle v_{ef}(r)=\frac{b^{2}e}{r^2}+4\left({\left(\frac{1}{r}\right)}^{12}-{\left(\frac{1}{r}\right)}^6\right)}$

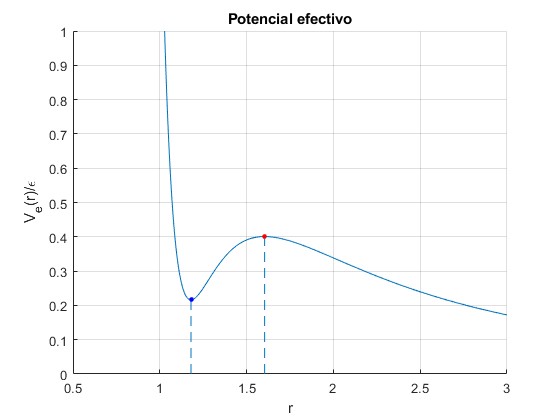
Para eb²=1.6 observamos la presencia de un mínimo y máximo local

k=1.6; %b^2e
g=@(x) k./x.^2+4*(1./x.^12-1./x.^6);
hold on
fplot(g, [0.8,3])
f=@(x) 24/x^10-12/x^4+k;
min=fzero(f,[1,1.5]);
max=fzero(f,[1.5,2]);
line([min,min],[0, g(min)],'lineStyle','--')
line([max,max],[0, g(max)],'lineStyle','--')
plot(min,g(min),'bo','markersize',3,'markerfacecolor','b')
plot(max,g(max),'ro','markersize',3,'markerfacecolor','r')
hold off
grid on
ylim([0,1])
xlabel('r')
ylabel('V_e(r)/\epsilon')
title('Potencial efectivo')

La condición de extremo (máximo o mínimo)

${\displaystyle \begin{array}{l}\frac{d{v}_{ef}}{dr}=-\frac{2}{r}\frac{b^{2}e}{r^2}+4\left(-\frac{12}{r}{\left(\frac{1}{r}\right)}^{12}+\frac{6}{r}{\left(\frac{1}{r}\right)}^6\right)=0\\ b^{2}e=-\frac{24}{r^{10}}+\frac{12}{r^4}\end{array}}$

Obtenemos la raíz de esta ecuación utilizando el procedimiento fzero de MALTAB, en el inervalo [1,1.5] (mínimo) y [1.5,2] máximo locales

Obtenemos órbitas circulares de radio r_M inestables cuando la energía total e es igual al máximo

${\displaystyle \begin{array}{l}e=\frac{b^{2}e}{r^2}+4\left({\left(\frac{1}{r}\right)}^{12}-{\left(\frac{1}{r}\right)}^6\right)\hfill \\ b^{2}e=\frac{e{r}^{12}-4\left(1-r^6\right)}{r^{10}}\hfill \end{array}}$

Sustituyendo eb² en la condición de extremo

${\displaystyle \begin{array}{l}\frac{e{r}^{12}-4\left(1-r^6\right)}{r^{10}}=-\frac{24}{r^{10}}+\frac{12}{r^4}\\ e{r}^{12}-8r^6+20=0\\ e{x}^2-8x+20=\mathrm{0,}x=r^6\\ x=\frac{4\pm 2\sqrt{4-5e}}{e}\\ r_M={\left(\frac{4+2\sqrt{4-5e}}{e}\right)}^{1/6}\end{array}}$

Para e>0.8 el término bajo la raíz se convierte en negativo y un valor real no existe para r_M

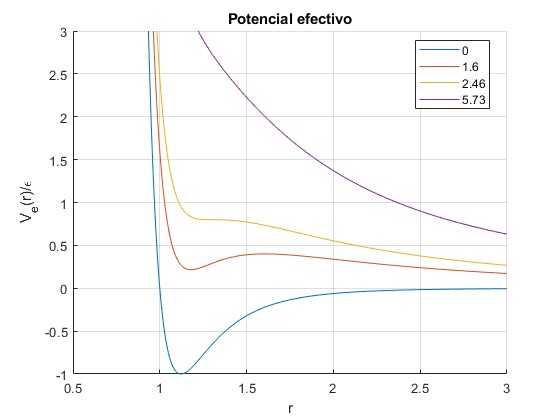
Cuando eb² se incrementa desaparecen el máximo y mínimo locales

hold on
for k=[0,1.6, 2.46,5.73]
    fplot(@(x) k./x.^2+4*(1./x.^12-1./x.^6), [0.8,3],'displayName',num2str(k))
end
hold off
grid on
legend('-DynamicLegend','location','best')
ylim([-1,3])
xlabel('r')
ylabel('V_e(r)/\epsilon')
title('Potencial efectivo')

Trayectorias

La fuerza conservativa correspondiente al potencial V(r) es

${\displaystyle F=-\frac{dV(r)}{dr}=4\epsilon \left(\frac{12}{r}{\left(\frac{\ell }{r}\right)}^{12}-\frac{6}{r}{\left(\frac{\ell }{r}\right)}^6\right)}$

Las ecuaciones del movimiento de la partícula de masa m son

${\displaystyle \begin{array}{l}m\frac{d^{2}x}{d{t}^2}=F\frac{x}{r}=4\epsilon \left(\frac{12}{r^2}{\left(\frac{\ell }{r}\right)}^{12}-\frac{6}{r^2}{\left(\frac{\ell }{r}\right)}^6\right)x\\ m\frac{d^{2}y}{d{t}^2}=F\frac{y}{r}=4\epsilon \left(\frac{12}{r^2}{\left(\frac{\ell }{r}\right)}^{12}-\frac{6}{r^2}{\left(\frac{\ell }{r}\right)}^6\right)y\end{array}}$

Para simplificar, resolvemos el sistema de dos ecuaciones diferenciales tomando m=ε=l=1

${\displaystyle \begin{array}{l}\{\begin{array}{l}\frac{d^{2}x}{d{t}^2}=-24\left(\frac{1}{r^8}-\frac{2}{r^{14}}\right)x\\ \frac{d^{2}y}{d{t}^2}=-24\left(\frac{1}{r^8}-\frac{2}{r^{14}}\right)y\end{array}\\ \begin{array}{l}r=\sqrt{x^2+y^2}\hfill \end{array}\end{array}}$

Representamos la trayectoria para la energía E y parámetros de impacto b=0.1, 0.2, 0.3....3.

El ángulo de dispersión Φ que forma la direccón de la velocidad v₀ para r→∞ es

${\displaystyle \tan \Phi =\frac{v_{0y}}{v_{0x}}}$

En MATLAB utilizamos la función atan2 que devuelve el ángulo entre -π y π

Ejemplos

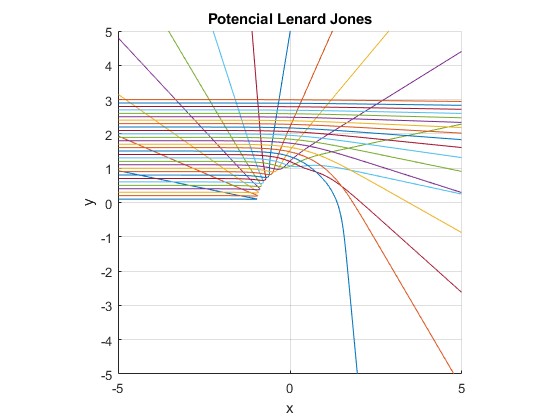
• Para la energía E=0.4

function lenard_jones
    E=0.4; %energía de la partícula
    opts=odeset('events',@stop_particula);
    fg=@(t,x)[x(2);-24*x(1)*(1/(x(1)^2+x(3)^2)^4-2/(x(1)^2+x(3)^2)^7); x(4); 
-24*x(3)*(1/(x(1)^2+x(3)^2)^4-2/(x(1)^2+x(3)^2)^7)];
    hold on
    for b=0.1:0.1:3 %parámetros de impacto
        [~,x]=ode45(fg,[0,100],[-10,sqrt(2*E),b,0], opts);
        plot(x(:,1),x(:,3))
        angulo=atan2(x(end,4),x(end,2));
        disp([b,angulo*180/pi])
    end
    hold off
    grid on
    xlabel('x')
    ylabel('y');
    xlim([-5,5])
    ylim([-5,5])
    axis square
    title('Potencial Lenard Jones')

    function [value,isterminal,direction]=stop_particula(~,x)
       %x(1) es  x, x(3) es y
        value=sqrt(x(1)^2+x(3)^2)-20;
        isterminal=1;    
        direction=0; 
    end
end



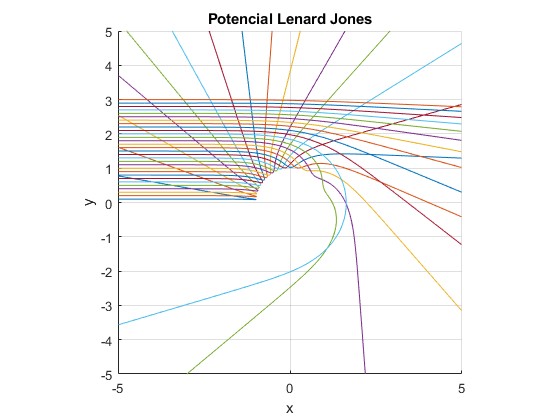
Los ángulos de dispersión Φ (aproximados) correspondientes a cada parámetro de impacto b son

   
    0.1000  170.0809
    0.2000  160.0148
    0.3000  150.0647
    0.4000  139.8414
    0.5000  129.5016
    0.6000  118.8111
    0.7000  107.9732
    0.8000   96.7881
    0.9000   85.8696
    1.0000   75.8970
    1.1000   60.1251
    1.2000   48.1580
    1.3000   31.8641
    1.4000   15.7014
    1.5000   -2.3396
    1.6000  -23.3307
    1.7000  -48.8725
    1.8000  -85.7355
    1.9000 -140.1201
    2.0000 -163.5271
    2.1000  -37.8542
    2.2000  -22.5957
    2.3000  -15.2522
    2.4000  -10.9142
    2.5000   -8.1157
    2.6000   -6.1692
    2.7000   -4.7987
    2.8000   -3.7669
    2.9000   -2.8548
    3.0000   -2.4243

Representamos el ángulo de dispersión Φ (en grados) en función del parámetro de impacto b. Cuando b se hace grande el ángulo Φ→0.

b=0.1:0.1:3;
angulos=[170.1,160.0,150.1,139.8,129.5,118.8,107.0, 96.8, 85.9,
 75.9, 60.1, 48.2, 31.9, 15.7, -2.3,-23.3,-48.9,-85.7,-140.1,
-163.5,-37.8,-22.6,-15.2,-10.9, -8.1, -6.2, -4.8, -3.8, -2.8, -2.4];
plot(b,angulos,'ro','markersize',3,'markerfacecolor','r')
grid on
xlabel('b')
ylabel('\Phi')
title('Angulo de dispersión')



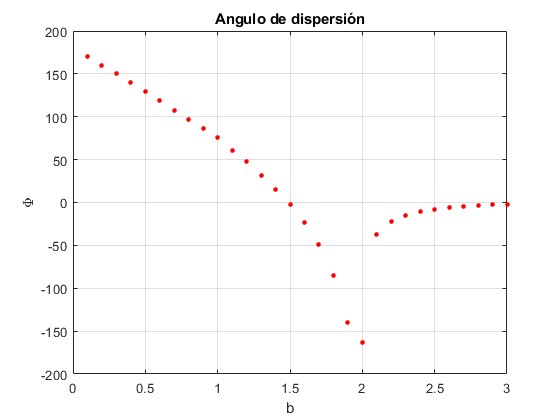
Un estudio más detallado nos informa que para los parámetros de impacto b≈2, la partícula puede dar vueltas alrededor del centro de fuerzas situado en el origen

function lenard_jones_6
    E=0.4; %energía de la partícula
    opts=odeset('events',@stop_particula);
    fg=@(t,x)[x(2);-24*x(1)*(1/(x(1)^2+x(3)^2)^4-2/(x(1)^2+x(3)^2)^7); x(4); 
-24*x(3)*(1/(x(1)^2+x(3)^2)^4-2/(x(1)^2+x(3)^2)^7)];
     b=1.9978; %parámetro de impacto
     [~,x]=ode45(fg,[0,100],[-10,sqrt(2*E),b,0], opts);
     plot(x(:,1),x(:,3))
    grid on
    xlabel('x')
    ylabel('y');
    xlim([-5,5])
    ylim([-5,5])
    axis square
    title('Potencial Lenard Jones')

    function [value,isterminal,direction]=stop_particula(~,x)
       %x(1) es  x, x(3) es y
        value=sqrt(x(1)^2+x(3)^2)-20;
        isterminal=1;   
        direction=0; 
    end
end



• Para la energía E=0.9



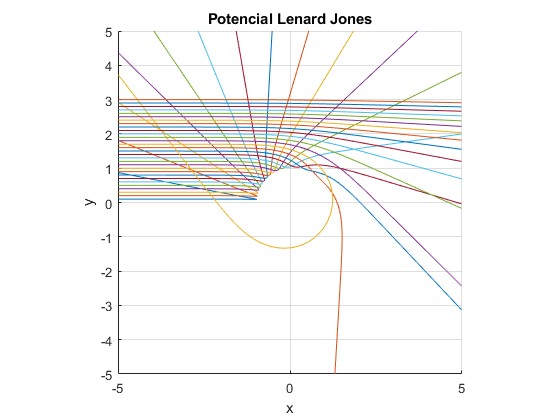
• Para la energía E=1.5

Actividades

Representamos la trayectoria de la partícula para una energía E y un parámetro de impacto b

Se introduce

• La energía E en el control titulado Energía
• El Parámetro de impacto b en el control titulado Parámetro de impacto

Se pulsa el botón titulado Nuevo

Se comprueba que el momento angular y la energía permanecen constantes en todos los puntos de la trayectoria

Se proporciona los datos de la posición (x,y) y de la velocidad (v_x,v_y) de la partícula en cada instante t. El ángulo de dispersión Φ en grados, medido cuando la partícula se aleja del origen a una distancia grande

Si la energía en un punto de la trayectoria difiere de la energía inicial, el programa calcula el % de error, si éste es mayor que 1 el programa se detiene

Referencias

Thomas Curtright, Gaurav Verma. Scattering shadows. Am. J. Phys. 92 (12), December 2024, pp. 924-930

Problema propuesto en la XLII Olimpiada Internacional de Física. Bangkok (2011)

Tiago Kroetz. An overview of classical scattering by a Lennard-Jones potential. Eur. J. Phys. 46 (2025) 055001