Movimiento de una partícula cargada en la superficie de un cono, bajo la influencia de un dipolo eléctrico situado en su vértice
Dipolo eléctrico
En la página titulada Campo eléctrico de un sistema de dos o más cargas eléctricas, calculamos las componenetes del campo eléctrico producido en un punto P por un dipolo eléctrico cuyo vector , está orientado a lo largo del eje X. En este apartado, repetimos la derivación para un dipolo cuyo vector tiene la dirección del eje Z
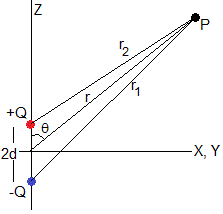
El potencial en el punto P distante r1 de la carga –Q y r2 de la carga +Q es
Expresamos r1 y r2 en función de r y θ, que es la posición del punto P expresada en coordenadas esféricas.
Teniendo en cuenta que d es pequeño frente a r, el potencial V se aproxima a
Las componentes de se pueden calcular a partir del gradiente de V
Carga positiva
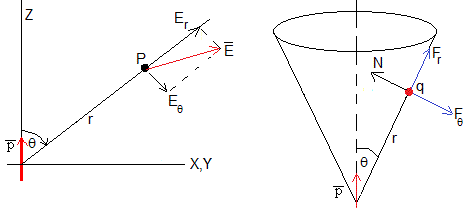
En la parte derecha de la figura, se muestran las fuerzas que ejerce el dipolo situado en el vértice del cono sobre una partícula de masa m y carga positiva q situada en la superficie del cono (de ángulo 2θ) a una distancia r del vértice. La superficie del cono ejerce sobre la partícula una fuerza N
No se incluye al peso mg de la partícula, ya que la fuerzas gravitatorias son muy pequeñas frente a las fuerzas eléctricas
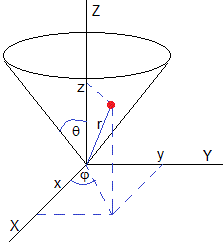
En un instante dado t, la partícula dista r del vértice del cono y hace un ángulo φ con el eje X tal como se muestra en la figura. Describimos el movimiento de la partícula en coordenadas esféricas (r, φ, θ) con el ángulo θ constante.
La aceleración en coordenadas esféricas es
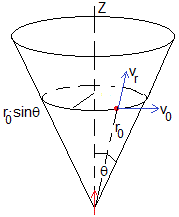
Las condiciones iniciales son
En el instante t=0, la partícula cargada se encuentra sobre la superficie cónica a una distancia r0 del dipolo y las componentes de su velocidad son vr en la dirección radial y v0 en la direccíon tangente a la circunferencia de radio r0sinθ. En el instante inicial, el ángulo φ=0
Ecuaciones del movimiento
Dado que θ es constante en la superficie del cono, dθ/dt=0
Dirección perpendicular a la superficie cónica,
Dirección tangente a la superficie cónica,
Dirección radial,
No hay fuerza en esta dirección, el momento angular Lz se mantiene constante
La reacción N de la superficie cónica es siempre positiva, la partícula desliza sin rozamiento sobre dicha superficie
Hemos definido una nueva velocidad vc
La aceleración en la dirección radial es positiva, por tanto no es posible que la partícula cargada describa un movimiento circular. La partícula se mueve radialmente a la vez que gira alrededor del eje Z
Distancia r de la partícula al dipolo en función del tiempo
Integramos la ecuación diferencial para obtener la velocidad radial dr/dt en función de la distancia r al dipolo, sabiendo que la velocidad inicial en la dirección radial es vr en la posición r0
Integramos, de nuevo, para obtener la distancia r de la partícula cargada al dipolo en función del tiempo
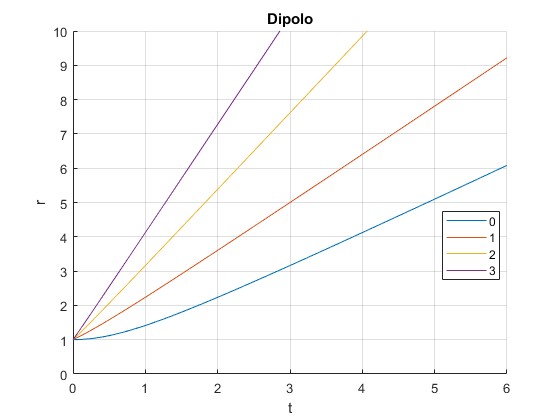
Representamos r en función del tiempo t para cuatro valores del cociente vr/vc=, 0, 1, 2, 3, con r0=1
r0=1;
vc=1;
hold on
for vr=0:3
f=@(t) sqrt(((vr^2+vc^2)*t+vr*r0).^2+vc^2*r0^2)/sqrt(vr^2+vc^2);
fplot(f,[0,6],'displayName',num2str(vr))
end
hold off
grid on
ylim([0,10])
legend('-DynamicLegend','location','best')
xlabel('t')
ylabel('r')
title('Dipolo')
Angulo φ en función del tiempo
Partimos de la constancia del momento angular Lz y de la expresión de la distancia r en función del tiempo
Resolvemos la integral
El resultado es
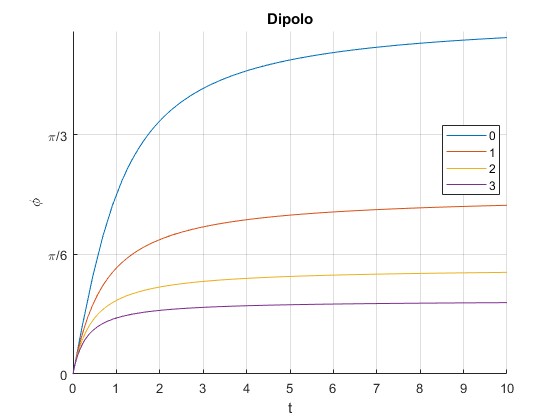
Representamos en función del tiempo t para cuatro valores del cociente vr/vc=, 0, 1, 2, 3, con r0=1
r0=1;
vc=1;
hold on
for vr=0:3
f=@(t) (atan(((vr^2+vc^2)*t+vr*r0)/(vc*r0))-atan(vr/vc))/vc;
fplot(f,[0,10],'displayName',num2str(vr))
end
hold off
grid on
set(gca,'YTick',0:pi/6:pi/2)
set(gca,'YTickLabel',{'0','\pi/6','\pi/3','\pi/2'})
legend('-DynamicLegend','location','best')
xlabel('t')
ylabel('\phi')
title('Dipolo')
Ecuación de la trayectoria
Partimos de la expresión de la velocidad en la dirección radial dr/dt y de la constancia del momento angular Lz
Hacemos el cambio de variable
El resultado es
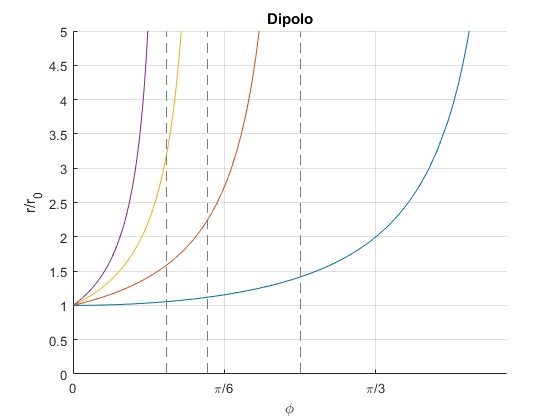
Representamos r en función del tiempo φ para cuatro valores del cociente vr/vc=, 0, 1, 2, 3, con
vc=1;
hold on
for vr=0:3
f=@(x) (vc/sqrt(vc^2+vr^2))./sin(asin(vc/sqrt(vc^2+vr^2))-x);
fplot(f,[0,1.5])
end
hold off
set(gca,'XTick',0:pi/6:pi/2)
set(gca,'XTickLabel',{'0','\pi/6','\pi/3','\pi/2'})
grid on
ylim([0,5])
xlabel('\phi')
ylabel('r/r_0')
title('Dipolo')
Carga negativa
Cuando la carga q es negativa, la reacción N de la superficie cónica no es siempre positiva,
La velocidad inicial v0 tiene que ser mayor que un valor mínimo, para que la partícula permanezca en la superficie del cono
La ecuación del movimiento en la dirección radial es
Supondremos que la velocidad inicial en la dirección radial vr=0. Los posibles movimientos son
Aceleración radial nula, movimiento circular
La velocidad inicial v0 es mayor que la crítica v0c
La velocidad inicial v0 es menor que la crítica v0c
La velocidad inicial de la partícula v0c (crítica) para que describa un movimiento circular es
Esta velocidad debe ser mayor que la mínima (N>0) lo que impone cierta condición al ángulo θ del cono
El momento angular Lz=mr0v0sinθ es independiente de la distancia r0 de la partícula al dipolo situado en el vértice el cono
La energía de la partícula es nula
Expresamos la ecuación diferencial del movimiento en la dirección radial en términos de v0c
Integramos la ecuación diferencial para obtener la velocidad radial dr/dt en función de la distancia r al dipolo, sabiendo que la velocidad inicial en la dirección radial es vr=0 en la posición r0
Integramos, para obtener la distancia radial r en función del tiempo
Ecuación de la trayectoria
Partimos de la expresión de la velocidad en la dirección radial dr/dt y de la constancia del momento angular Lz
Hacemos el cambio de variable
El resultado es
Expresamos la ecuación diferencial del movimiento en la dirección radial en términos de v0c
Integramos la ecuación diferencial para obtener la velocidad radial dr/dt en función de la distancia r al dipolo, sabiendo que la velocidad inicial en la dirección radial es vr=0 en la posición r0
Ecuación de la trayectoria
Partimos de la expresión de la velocidad en la dirección radial dr/dt y de la constancia del momento angular Lz
Hacemos el cambio de variable
Hacemos un nuevo cambio de variable
El resultado es
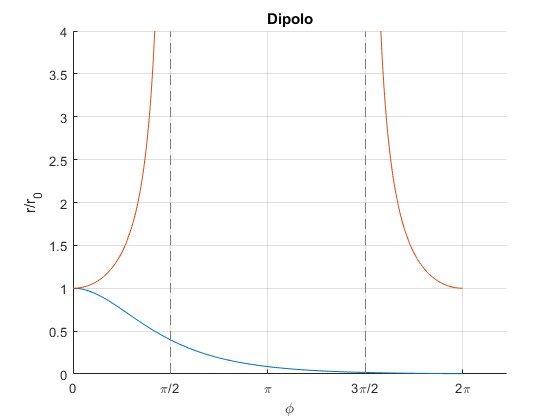
Representamos r en función del ángulo φ para v0>v0c con . Representamos r en función del ángulo φ para v0<v0c con
r0=1;
vc=1;
hold on
f=@(x) 1./cosh(x);
fplot(f,[0,2*pi])
f=@(x) 1./cos(x);
fplot(f,[0,2*pi])
hold off
set(gca,'XTick',0:pi/2:2*pi)
set(gca,'XTickLabel',{'0','\pi/2','\pi','3\pi/2','2\pi'})
grid on
ylim([0,4])
xlabel('\phi')
ylabel('r/r_0')
title('Dipolo')
Referencias
Yusmantoro Yusmantoro. Circular motion of a charged particle on the inner surface of a frictionless cone under the influence of an electric field due to an electric dipole. Eur. J. Phys. 45 (2024) 065201

