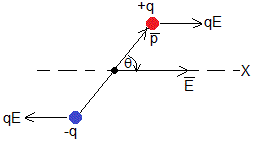
Sea un dipolo eléctrico en el seno de un campo eléctrico uniforme cuya dirección es el eje X.

La fuerza que ejerce el campo eléctrico sobre cada una de las cargas es qE

El momento de dichas fuerzas respecto del eje del dipolo

• Tiene por módulo, 2qE·(d/2)sinθ=qdEsinθ=pEsinθ. Donde p es el momento dipolar
• Dirección, perpendicular al plano del dipolo
• Sentido, el de las agujas del reloj

En forma vectorial

${\displaystyle \overrightarrow{M}=\overrightarrow{p}\times \overrightarrow{E}}$

Un dipolo en un campo eléctrico uniforme oscila como un péndulo simple. La ecuación de la dinámica de rotación es

${\displaystyle \begin{array}{l}\left(m{\left(\frac{d}{2}\right)}^2+m{\left(\frac{d}{2}\right)}^2\right)\frac{d^2\theta }{d{t}^2}=-pE\sin \theta \\ \frac{d^2\theta }{d{t}^2}+\frac{2qE}{md}\sin \theta =0\end{array}}$

Si las oscilaciones son de amplitud pequeña, se puede aproximar sinθ≈θ. El periodo del Movimiento Armónico Simple que describe es

${\displaystyle P=2\pi \sqrt{\frac{md}{2qE}}}$

Movimiento de la molécula

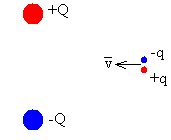
En la figura, se muestra un par de esferas con cargas +Q y –Q respectivamente, separadas una distancia 2D, y una molécula de momento dipolar p=q·d, siendo 2d la separación entre los centros de distribución de las cargas positivas y negativas, respectivamente.

La molécula está sometida a cuatro fuerzas: dos de repulsión entre cargas del mismo signo y otras dos de atracción entre cargas de signo contrario. Como las cargas de signo contrario están más cerca, predomina la fuerza de atracción sobre la de repulsión.

Si en el instante en el que la molécula llega al centro de las esferas, se conectasen a potencial cero, la molécula continuaría con velocidad constante. 

Un dispositivo de este tipo formado por varias etapas constituye un acelerador de moléculas que permite estudiar su estructura a partir de los choques inelásticos que experimentan.

Un acelerador de moléculas tiene unos electrodos de forma esférica de 0.25 mm de radio, separados 2D=1 mm, que se mantienen a un potencial de ±40 kV. Una molécula de momento dipolar p=2·10^-29 C·m adquiere una energía de aproximadamente 0.01 eV. Como esta energía es muy pequeña, el acelerador consta de 700 etapas separadas 1.4 cm, los electrodos se alimentan por un potencial alterno de 500 kHz. .

En la experiencia simulada mantendremos la carga de los dos electrodos esféricos constante e igual a ±Q. Observaremos como la molécula describe un movimiento oscilatorio, que no es Armónico Simple (MAS).

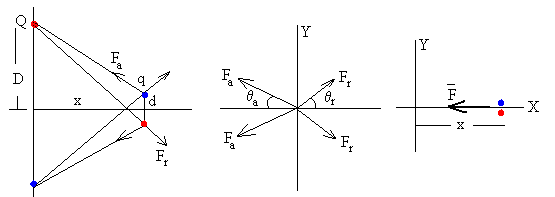
Por simetría, las componentes a lo largo del eje Y de las fuerzas que actúan sobre la molécula se anulan de dos en dos. La resultante está dirigida a lo largo del eje X y vale

F=-2·F_a·cosθ_a+2·F_r·cosθ_r

Siendo F_a el módulo de la fuerza atractiva entre cargas de distinto signo, y F_r el módulo de la fuerza repulsiva entre cargas del mismo signo.

${\displaystyle F_a=\frac{1}{4\pi {\epsilon }_0}\frac{qQ}{\left(x^2+{(D-d)}^2\right)}{F}_r=\frac{1}{4\pi {\epsilon }_0}\frac{qQ}{\left(x^2+{(D+d)}^2\right)}}$

Los ángulos que forman los vectores fuerza con el eje X son, respectivamente

${\displaystyle \cos {\theta }_a=\frac{x}{\sqrt{x^2+{(D-d)}^2}}\cos {\theta }_r=\frac{x}{\sqrt{x^2+{(D+d)}^2}}}$

La expresión de la fuerza resultante es

${\displaystyle F=\frac{qQx}{2\pi {\epsilon }_0}\left(\frac{1}{{\left(x^2+{(D+d)}^2\right)}^{3/2}}-\frac{1}{{\left(x^2+{(D-d)}^2\right)}^{3/2}}\right)}$

• Si x>0, la resultante de las fuerzas F<0
• Si x<0, la resultante de las fuerzas F>0

La fuerza F es de signo contrario al desplazamiento x, pero no es proporcional al desplazamiento, que es la característica distintiva de un Movimiento Armónico Simple.

La ecuación del movimiento es

${\displaystyle m\frac{d^{2}x}{d{t}^2}=\frac{qQx}{2\pi {\epsilon }_0}\left(\frac{1}{{\left(x^2+{(D+d)}^2\right)}^{3/2}}-\frac{1}{{\left(x^2+{(D-d)}^2\right)}^{3/2}}\right)}$

Esta ecuación diferencial se resuelve por procedimientos numéricos con las condiciones iniciales t=0, x=x₀ dx/dt=0. La molécula parte de la posición x₀ con velocidad inicial nula.

Balance energético

En la posición x, la energía de la molécula es la suma de la energía cinética y potencial

${\displaystyle E=\frac{1}{2}m{v}^2+\frac{1}{4\pi {\epsilon }_0}\left(\frac{2qQ}{\sqrt{x^2+{(D+d)}^2}}-\frac{2qQ}{\sqrt{x^2+{(D-d)}^2}}\right)}$

Cuando pasa por el origen, la energía de la molécula es

${\displaystyle E=\frac{1}{2}m{v}^2+\frac{1}{4\pi {\epsilon }_0}\left(\frac{2qQ}{D+d}-\frac{2qQ}{D-d}\right)}$

Cuando parte de la posición inicial x₀ o llega al extremo opuesto de la trayectoria –x₀, la velocidad de la molécula v=0.

${\displaystyle E=\frac{1}{4\pi {\epsilon }_0}\left(\frac{2qQ}{\sqrt{x_0^2+{(D+d)}^2}}-\frac{2qQ}{\sqrt{x_0^2+{(D-d)}^2}}\right)}$

Aplicando el principio de conservación de la energía, calculamos la velocidad v de la molécula en cualquier posición x.

Ejemplo

Datos

• Separación entre los electrodos esféricos, 2D=1
• Separación entre los centros de distribución de carga de la molécula polar 2d=1/2
• Cargas de la molécula polar q=1
• Carga de los electrodos Q=6
• Valor de la constante 1/(4πє₀)=1

La fuerza sobre la partícula en la posición x=2 es

${\displaystyle \begin{array}{l}F=\frac{qQx}{2\pi {\epsilon }_0}\left(\frac{1}{{\left(x^2+{(D+d)}^2\right)}^{3/2}}-\frac{1}{{\left(x^2+{(D-d)}^2\right)}^{3/2}}\right)\\ F=2\frac{1·6·2}{1}\left(\frac{1}{{\left(2^2+{(0.5+0.25)}^2\right)}^{3/2}}-\frac{1}{{\left(2^2+{(0.5-0.25)}^2\right)}^{3/2}}\right)=-0.468\end{array}}$

La energía de la partícula en la posición inicial  x₀=3 es

${\displaystyle \begin{array}{l}E=\frac{1}{4\pi {\epsilon }_0}\left(\frac{2qQ}{\sqrt{x_0^2+{(D+d)}^2}}-\frac{2qQ}{\sqrt{x_0^2+{(D-d)}^2}}\right)\\ E=1·\left(\frac{2·1·6}{\sqrt{3^2+{(0.5+0.25)}^2}}-\frac{2·1·6}{\sqrt{3^2+{(0.5-0.25)}^2}}\right)=-0.1056\end{array}}$

La energía cuando pasa por la posición x=2 es

${\displaystyle \begin{array}{l}E=\frac{1}{2}m{v}^2+\frac{1}{4\pi {\epsilon }_0}\left(\frac{2qQ}{\sqrt{x^2+{(D+d)}^2}}-\frac{2qQ}{\sqrt{x^2+{(D-d)}^2}}\right)\\ \text{-0}\text{.1056}=\frac{\text{1}}{\text{2}}1·v^2+1·\left(\frac{2·1·6}{\sqrt{2^2+{(0.5+0.125)}^2}}-\frac{2·1·6}{\sqrt{2^2+{(0.5-0.125)}^2}}\right)\end{array}}$

Se despeja la velocidad de la molécula v=0.678

El procedimiento ode45 de MATLAB no produce buenos resultados

q=1;
Q=6;
d=1/4;
D=0.5;
x0=[3,0];
f=@(t,x) [x(2);2*q*Q*x(1)*((x(1)^2+(D+d)^2)^(-3/2)-
((x(1)^2+(D-d)^2)^(-3/2)))]; 
[t,x]=ode45(f,[0,30],x0);
plot(t,x(:,1))
xlabel('t')
ylabel('x');
title('Movimiento de una molécula')
grid on

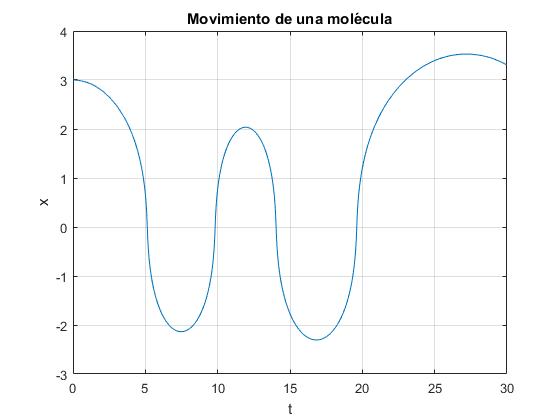
Comprobamos la conservación de la energía. Como apreciamos, la energía inicial no se mantiene constante

>> E=2*q*Q*(sqrt(x0(1)^2+(D+d)^2)-sqrt(x0(1)^2+(D-d)^2))
E =    0.9832
>> E=0.5*x(:,2).^2+2*q*Q*(sqrt(x(:,1).^2+(D+d)^2)-sqrt(x(:,1).^2+(D-d)^2))
E =
    0.9832
    0.9832
    0.9832
    .....
    2.0345
    2.1429
    ......
    10.8802
    12.5506
    14.8270
    18.0371
    22.6982
    26.3133
    30.5965
    34.9475
    37.7536
    37.0530
    33.6128
    29.1141
   ......

Actividades

En la simulación se fijado los siguientes parámetros:

• 1/(4πє₀)=1,

• La masa del la molécula es m=1, y sus cargas ±q=±1. La separación d es una fracción de la separación 2D entre las esferas.

• La carga Q de las esferas es múltiplo de q, y su separación es 2D=1 unidad de longitud.

• La posición de la molécula en el instante t=0, es x₀=3 unidades de longitud

Se introduce

• La carga Q de las dos esferas, en el control titulado Carga

• La separación entre las cargas ±q de la molécula, seleccionado una fracción en el control titulado Separación

Se pulsa el botón titulado Nuevo

Se observa el movimiento de la molécula entre las posiciones extremas ±x₀, y se puede medir el periodo P de la oscilación. La fuerza sobre la molécula es de corto alcance ya que solamente tiene un valor apreciable cuando pasa por las proximidades del origen.

En la parte superior, se representa la energía potencial E_p(x), que presenta un mínimo en x=0.

${\displaystyle E_p(x)=\frac{1}{4\pi {\epsilon }_0}\left(\frac{2qQ}{\sqrt{x^2+{(D+d)}^2}}-\frac{2qQ}{\sqrt{x^2+{(D-d)}^2}}\right)}$

Se representa mediante una recta horizontal la energía total E. Un segmento vertical de color rojo, representa la energía cinética E_k, diferencia entre la energía total E y la energía potencial E_p(x). Una flecha representa la fuerza sobre la partícula, la pendiente cambiada de signo de la curva de la energía potencial en la posición x.

${\displaystyle F=-\frac{d{E}_p(x)}{dx}}$

La fuerza F es nula en el origen x=0 (posición de equilibrio), donde la energía potencial E_p(x) presenta un mínimo

El programa calcula en cada instante el tanto por ciento de error relativo en la energía o el cociente

${\displaystyle \left|\frac{E-E_0}{E_0}\right|·100}$

donde E es la energía del sistema en cualquier instante tt, y E₀ es la energía inicial del sistema.

Este valor se proporciona en caracteres de color rojo en la parte inferior izquierda. Su valor debe ser siempre cero, o un valor muy pequeño lo que indica que la energía del sistema permanece constante y el programa realiza los cálculos correctamente.

Referencias

Lorrain P. Corson D., Campos y Ondas Electromagnéticas, Editorial Selecciones Científicas (1972), págs. 144-145