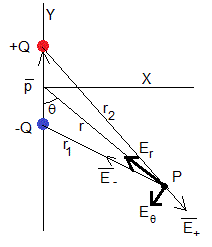
Consideremos el campo eléctrico producido por un dipolo de momento $\overrightarrow{p}$, módulo, Q(2d), a lo largo del eje Y, tal como se muestra en la figura. El dipolo está formado por dos cargas +Q y -Q separadas una distancia 2d. E₊ es el campo eléctrico producido por la carga positiva y E_- el producido por la negativa en el punto P de coordenadas (r, θ). Se señalan las componentes tangencial E_θ y radial E_r del campo resultante.

La energía potencial vale

${\displaystyle \begin{array}{l}V=\frac{Q}{4\pi {\epsilon }_0}\left(\frac{1}{r_2}-\frac{1}{r_1}\right)\\ \begin{array}{l}{r}_1^2=r^2+d^2-2rd\cos \theta \hfill \\ r_2^2=r^2+d^2+2rd\cos \theta \hfill \end{array}\end{array}}$

Despreciando los términos de orden superior a d²/r², obtenemos

${\displaystyle V=-\frac{Qd}{2\pi {\epsilon }_0{r}^2}\cos \theta }$

Las componentes del campo eléctrico $\overrightarrow{E}$ son

${\displaystyle \begin{array}{l}{E}_r=-\frac{\partial V}{\partial r}=-\frac{1}{4\pi {\epsilon }_0}\frac{4Qd}{r^3}\cos \theta \hfill \\ E_{\theta }=-\frac{1}{r}\frac{\partial V}{\partial \theta }=-\frac{1}{4\pi {\epsilon }_0}\frac{2Qd}{r^3}\sin \theta \hfill \end{array}}$

La fuerza que ejerce este campo eléctrico sobre una carga positva +q situada en el punto P tiene la misma dirección y sentido que el campo $\overrightarrow{F}=q\overrightarrow{E}$

Analogía con el péndulo simple

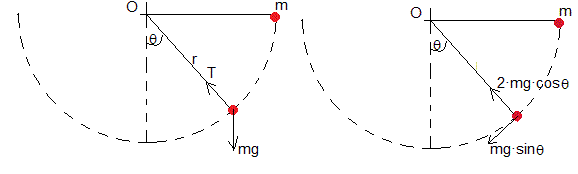
Sea un péndulo formado por una masa puntual m unida a un hilo inextensible de longitud r. En la dirección radial, la fuerza sobre la partícula está dirigida hacia el centro y su valor es T-mgcosθ. La fuerza en la dirección tangencial es mgsinθ

Como la partícula de masa m está describiendo un movimiento circular de radio r, la ecuación de la dinámica del movimiento circular uniforme es

${\displaystyle m\frac{v^2}{r}=T-mg\cos \theta }$

La velocidad v se calcula aplicando el principio de conservación de la energía a un péndulo que se ha desviado π/2 (90°) y se suelta. Situando el nivel cero de energía potencial en O

${\displaystyle \frac{1}{2}m{v}^2-mgr\cos \theta =0}$

La tensión T=3mgcosθ, y la fuerza en la dirección radial sobre la partícula es F_r=2mgcosθ

En ambos casos (carga en el campo eléctrico producido por un dipolo y péndulo simple) tenemos:

• La fuerza en la dirección radial dirigida hacia el centro vale, 2k·cosθ
• la fuerza en la dirección tangencial vale, k·sinθ

Donde la constante de proporcionalidad, k=mg en el caso del péndulo y $k=\frac{1}{4\pi {\epsilon }_0}\frac{2Qqd}{r^3}$, en el caso de la carga

Esta analogía solamente se produce en el caso de que la partícula cargada parta (en reposo) de un punto del eje X situado a una distancia r del origen y el péndulo de longitud r se desvíe un ángulo θ₀=π/2 (90°) y se suelte.

Movimiento de la carga

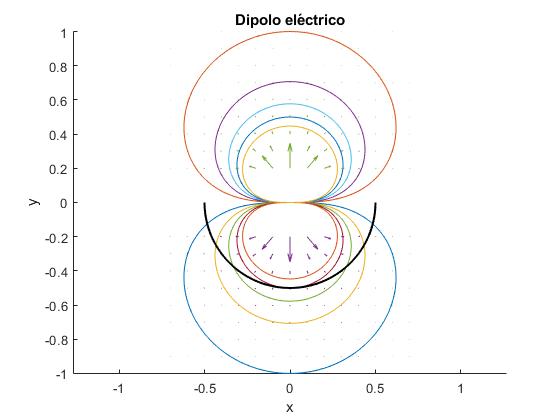
La carga se mueve en el campo eléctrico producido por el dipolo a lo largo de una semicircunferencia de radio r tal como se muestra en la figura en color negro. Repetiremos aquí los cálculos realizados para el péndulo en el caso particular de que la desviación θ₀=π/2

El principio de conservación de la energía para la carga q de masa m que se mueve en el campo producido por el dipolo es

${\displaystyle \begin{array}{l}\frac{1}{2}m{v}^2+qV=0\\ \frac{1}{2}m{v}^2-q\frac{Qd}{2\pi {\epsilon }_0{r}^2}\cos \theta =0\end{array}}$

Cuando θ=π/2, la energía es cero, como en el caso del péndulo. Como la carga se mueve en una trayectoria circular su velocidad v=r·dθ/dt

${\displaystyle \begin{array}{l}{\left(\frac{d\theta }{dt}\right)}^2=\frac{1}{r^4}\frac{qQd}{\pi {\epsilon }_{0}m}\cos \theta \\ {\displaystyle \underset{0}{\overset{\theta }{\int }}\frac{d\theta }{\sqrt{\cos \theta }}}=\frac{1}{r^2}\sqrt{\frac{qQd}{\pi {\epsilon }_{0}m}}t\end{array}}$

donde t es un cuarto de periodo. Teniendo en cuenta la relación trigonométrica

${\displaystyle \cos \theta ={\cos }^2\left(\frac{\theta }{2}\right)-{\sin }^2\left(\frac{\theta }{2}\right)=1-2{\sin }^2\left(\frac{\theta }{2}\right)}$

la integral se expresa

${\displaystyle {\displaystyle \underset{0}{\overset{\theta }{\int }}\frac{d\theta }{\sqrt{1-2{\sin }^2\left(\frac{\theta }{2}\right)}}}=\frac{1}{r^2}\sqrt{\frac{qQd}{\pi {\epsilon }_{0}m}}t}$

Haciendo el cambio de variable

${\displaystyle \begin{array}{l}\sin \left(\frac{\theta }{2}\right)=\frac{\sqrt{2}}{2}\sin \phi \hfill \\ \frac{1}{2}\cos \left(\frac{\theta }{2}\right)d\theta =\frac{\sqrt{2}}{2}\cos \phi ·d\phi \hfill \end{array}}$

Obtenemos la integral elíptica

${\displaystyle {\displaystyle \underset{0}{\overset{\phi }{\int }}\frac{d\phi }{\sqrt{1-\frac{1}{2}{\sin }^2\phi }}}=\frac{1}{r^2}\sqrt{\frac{qQd}{2\pi {\epsilon }_{0}m}}t}$

Para el límite θ=π/2, le corresponde el límite a φ=π/2 y t es un cuarto de periodo P. A la izquierda tendremos una integral elíptica completa de primera especie

${\displaystyle P=4r^2\sqrt{\frac{2\pi {\epsilon }_{0}m}{qQd}}K\left(\frac{\sqrt{2}}{2}\right)}$

>> ellipke(1/2)
ans =    1.8541

El movimiento de la carga se describe mediante la función elíptica de Jacobi sn

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{\phi }{\int }}\frac{d\phi }{\sqrt{1-\frac{1}{2}{\sin }^2\phi }}}=4K\left(\frac{\sqrt{2}}{2}\right)\frac{t}{P}\\ \theta =2\arcsin \left(\frac{\sqrt{2}}{2}\text{sn}\left(4K\left(\frac{\sqrt{2}}{2}\right)\frac{t}{P},\frac{1}{2}\right)\right)\end{array}}$

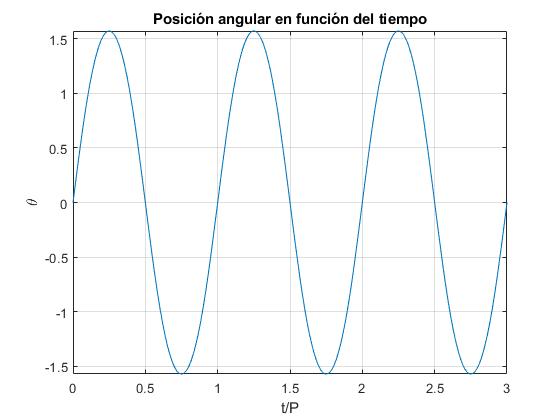
Representamos la posición angular θ en función del tiempo t/P, para tres periodos P. Supondremos que la carga sale de la posición θ=0, y alcanza la posición θ=π/2 después de un cuarto de periodo, el movimiento se repite como en el péndulo

k=sqrt(2)/2;
x=@(t) 2*asin(k*ellipj(4*ellipke(k^2)*t,k^2));
fplot(x, [0,3]);
xlabel('t/P')
ylabel('\theta')
title('Posición angular en función del tiempo')
grid on

Ecuaciones generales del movimiento

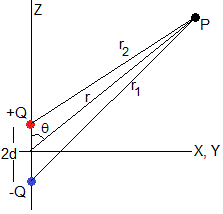
El potencial en el punto P distante r₁ de la carga –Q y r₂ de la carga +Q es

${\displaystyle V=\frac{Q}{4\pi {\epsilon }_0}\left(\frac{1}{r_2}-\frac{1}{r_1}\right)}$

Expresamos r₁ y r₂ en función de r y θ, que es la posición del punto P expresada en coordenadas esféricas.

${\displaystyle \begin{array}{l}{r}_1^2=r^2+d^2+2rd\cos \theta \\ r_2^2=r^2+d^2-2rd\cos \theta \end{array}}$

Teniendo en cuenta que la distacia d es pequeña frente a r, el potencial V se aproxima a

${\displaystyle V\approx \frac{2Qd}{4\pi {\epsilon }_0{r}^2}\cos \theta =\frac{p}{4\pi {\epsilon }_0{r}^2}\cos \theta }$

La velocidad en coordenadas esféricas es

${\displaystyle \frac{d\overrightarrow{r}}{dt}=\frac{dr}{dt}\widehat{r}+r\frac{d\widehat{r}}{dt}=\frac{dr}{dt}\widehat{r}+r\frac{d\theta }{dt}\widehat{\theta }+r\sin \theta ·\frac{d\phi }{dt}\widehat{\phi }}$

La energía cinética

${\displaystyle E_k=\frac{1}{2}m\left({\left(\frac{dr}{dt}\right)}^2+{\left(r\frac{d\theta }{dt}\right)}^2+{\left(r\sin \theta ·\frac{d\phi }{dt}\right)}^2\right)}$

La lagrangiana de la partícula de masa m y carga q, en el campo eléctrico producido por el dipolo situado en el origen

${\displaystyle L=E_k-E_p=\frac{1}{2}m\left({\left(\frac{dr}{dt}\right)}^2+{\left(r\frac{d\theta }{dt}\right)}^2+{\left(r\sin \theta ·\frac{d\phi }{dt}\right)}^2\right)-\frac{qp}{4\pi {\epsilon }_0{r}^2}\cos \theta }$

Las ecuaciones del movimiento son

${\displaystyle \begin{array}{l}L=E_k-E_p=\frac{1}{2}m\left({\left(\frac{dr}{dt}\right)}^2+{\left(r\frac{d\theta }{dt}\right)}^2+{\left(r\sin \theta ·\frac{d\phi }{dt}\right)}^2\right)-\frac{qp}{4\pi {\epsilon }_0{r}^2}\cos \theta \\ \frac{d}{dt}\left(\frac{\partial L}{\partial \dot{r}}\right)-\frac{\partial L}{\partial r}=0\\ m\frac{d^{2}r}{d{t}^2}-mr{\left(\frac{d\theta }{dt}\right)}^2-mr{\left(\sin \theta ·\frac{d\phi }{dt}\right)}^2-\frac{qp}{2\pi {\epsilon }_0{r}^3}\cos \theta =0\\ \frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\theta }}\right)-\frac{\partial L}{\partial \theta }=0\\ m\frac{d}{dt}\left(r^2\frac{d\theta }{dt}\right)-m{\left(r\frac{d\phi }{dt}\right)}^2\sin \theta \cos \theta -\frac{qp}{4\pi {\epsilon }_0{r}^2}\sin \theta =0\\ \frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\phi }}\right)-\frac{\partial L}{\partial \phi }=0\\ m\frac{d}{dt}\left(r^2{\sin }^2\theta \frac{d\phi }{dt}\right)=0\\ r^2{\sin }^2\theta \frac{d\phi }{dt}=\text{cte}\end{array}}$

Constantes del movimiento

Vamos a comprobar que la última constante del movimiento es la componente Z de momento angular. El vector momento angular en coordenadas esféricas es

${\displaystyle \overrightarrow{L}=\overrightarrow{r}\times m\overrightarrow{v}=m\left|\begin{array}{ccc}\widehat{r}& \widehat{\theta }& \widehat{\phi }\\ r& 0& 0\\ \frac{dr}{dt}& r\frac{d\theta }{dt}& r\sin \theta ·\frac{d\phi }{dt}\end{array}\right|=m\left(-r^2\sin \theta \frac{d\phi }{dt}\widehat{\theta }+r^2\frac{d\theta }{dt}\widehat{\phi }\right)}$

En la página titulada Coordenadas polares, cilíndricas y esféricas relacionamos los vectores unitarios, en particular, $\widehat{k}$, con $\widehat{r}$ y $\widehat{\theta }$

${\displaystyle L_z=\overrightarrow{L}·\widehat{k}=m\left(-r^2\sin \theta \frac{d\phi }{dt}\widehat{\theta }+r^2\frac{d\theta }{dt}\widehat{\phi }\right)·\left(\cos \theta \widehat{r}-\sin \theta \widehat{\theta }\right)=m{r}^2{\sin }^2\theta \frac{d\phi }{dt}}$

Hemos identificado la primera constante del movimiento, la componente Z del momento angular

La energía es una constante del movimiento por ser el campo eléctrico conservativo

${\displaystyle E=E_k+E_p=\frac{1}{2}m\left({\left(\frac{dr}{dt}\right)}^2+{\left(r\frac{d\theta }{dt}\right)}^2+{\left(r\sin \theta ·\frac{d\phi }{dt}\right)}^2\right)+\frac{qp}{4\pi {\epsilon }_0{r}^2}\cos \theta }$

Expresamos la energía de la forma

${\displaystyle \begin{array}{l}E=\frac{1}{2}m\left({\left(\frac{dr}{dt}\right)}^2+{\left(r\frac{d\theta }{dt}\right)}^2+{\left(r\sin \theta ·\frac{d\phi }{dt}\right)}^2\right)+\frac{qp}{4\pi {\epsilon }_0{r}^2}\cos \theta \\ E=\frac{1}{2}m{\left(\frac{dr}{dt}\right)}^2+\frac{\beta }{2m{r}^2}\\ \beta =m^2{r}^4{\left(\frac{d\theta }{dt}\right)}^2+\frac{L_z^2}{{\sin }^2\theta }+m\frac{qp}{2\pi {\epsilon }_0}\cos \theta \end{array}}$

Comprobaremos, más abajo, que β es una constante del movimiento

Ecuación del movimiento

• Multiplicamos la ecuación diferencial del movimiento en la dirección radial por mr y la de la energía por 2

${\displaystyle \begin{array}{l}mr\frac{d^{2}r}{d{t}^2}=m{r}^2{\left(\frac{d\theta }{dt}\right)}^2+m{r}^2{\left(\sin \theta ·\frac{d\phi }{dt}\right)}^2+\frac{qp}{2\pi {\epsilon }_0{r}^2}\cos \theta =0\\ 2E=m\left({\left(\frac{dr}{dt}\right)}^2+{\left(r\frac{d\theta }{dt}\right)}^2+{\left(r\sin \theta ·\frac{d\phi }{dt}\right)}^2\right)+\frac{qp}{2\pi {\epsilon }_0{r}^2}\cos \theta \end{array}}$

Restando la primera de la segunda, el resultado es la ecuación r=r(t)

${\displaystyle \begin{array}{l}mr\frac{d^{2}r}{d{t}^2}-2E=-m{\left(\frac{dr}{dt}\right)}^2\\ m\left(r\frac{d^{2}r}{d{t}^2}+{\left(\frac{dr}{dt}\right)}^2\right)=2E\\ \frac{d}{dt}\left(2r\frac{dr}{dt}\right)=\frac{4E}{m}\\ \frac{d}{dt}\left(\frac{d{r}^2}{dt}\right)=\frac{4E}{m}\\ \frac{d{r}^2}{dt}=\frac{4E}{m}t+2r_0{\left(\frac{dr}{dt}\right)}_0\\ r^2=\frac{1}{2}\frac{4E}{m}{t}^2+2r_0{\left(\frac{dr}{dt}\right)}_{0}t+r_0^2\end{array}}$

donde r₀ y ${\left(\frac{dr}{dt}\right)}_0$ son los valores iniciales de la posición r y velocidad dr/dt inicial en la dirección radial

El movimiento con r=cte solamente se produce si la energía E=0 es nula y ${\left(\frac{dr}{dt}\right)}_0=0$

• Alternativamente, la ecuación del movimiento en la dirección radial r=r(t)

${\displaystyle m\frac{d^{2}r}{d{t}^2}-mr{\left(\frac{d\theta }{dt}\right)}^2-mr{\left(\sin \theta ·\frac{d\phi }{dt}\right)}^2-\frac{qp}{2\pi {\epsilon }_0{r}^3}\cos \theta =0}$

Multiplicamos por mr³

${\displaystyle \begin{array}{l}{m}^2{r}^3\frac{d^{2}r}{d{t}^2}-m^2{r}^4{\left(\frac{d\theta }{dt}\right)}^2-m^2{r}^4{\left(\sin \theta ·\frac{d\phi }{dt}\right)}^2-m\frac{qp}{2\pi {\epsilon }_0}\cos \theta =0\\ m^2{r}^3\frac{d^{2}r}{d{t}^2}-m^2{r}^4{\left(\frac{d\theta }{dt}\right)}^2-\frac{L_z^2}{{\sin }^2\theta }-m\frac{qp}{2\pi {\epsilon }_0}\cos \theta =0\\ m^2{r}^3\frac{d^{2}r}{d{t}^2}-\beta =0\\ \frac{d^{2}r}{d{t}^2}=\frac{\beta }{m^2{r}^3}\end{array}}$

• Ecuación del movimiento θ=θ(t)

Separamos variables en la expresión de la constante β

${\displaystyle \begin{array}{l}\beta =m^2{r}^4{\left(\frac{d\theta }{dt}\right)}^2+\frac{L_z^2}{{\sin }^2\theta }+m\frac{qp}{2\pi {\epsilon }_0}\cos \theta \\ \sqrt{\beta -\frac{L_z^2}{{\sin }^2\theta }-m\frac{qp}{2\pi {\epsilon }_0}\cos \theta }=m{r}^2\left(\frac{d\theta }{dt}\right)\\ \frac{d\theta }{\sqrt{\beta -\frac{L_z^2}{{\sin }^2\theta }-m\frac{qp}{2\pi {\epsilon }_0}\cos \theta }}=\frac{dt}{r^2}\\ {\displaystyle \underset{{\theta }_0}{\overset{\theta }{\int }}\frac{d\theta }{\sqrt{\beta -\frac{L_z^2}{{\sin }^2\theta }-m\frac{qp}{2\pi {\epsilon }_0}\cos \theta }}={\displaystyle \underset{0}{\overset{t}{\int }}\frac{dt}{\frac{1}{2}\frac{4E}{m}{t}^2+2r_0{\left(\frac{dr}{dt}\right)}_{0}t+r_0^2}}}\end{array}}$

• Ecuación del movimiento φ=φ(t)

A partir de la expresión de la componente Z del momento angular

${\displaystyle \begin{array}{l}{L}_z=m{r}^2{\sin }^2\theta \frac{d\phi }{dt}\\ \phi ={\phi }_0+\frac{L_z}{m}{\displaystyle \underset{0}{\overset{t}{\int }}\frac{dt}{r^2{\sin }^2\theta }}\end{array}}$

β es una constante del movimiento

1. Conservación de la energía

Derivamos la energía E respecto del tiempo t

${\displaystyle \begin{array}{l}E=\frac{1}{2}m{\left(\frac{dr}{dt}\right)}^2+\frac{\beta }{2m{r}^2}\\ \frac{dE}{dt}=m\frac{dr}{dt}\frac{d^{2}r}{d{t}^2}-\frac{\beta }{m{r}^3}\frac{dr}{dt}=0\\ \frac{d^{2}r}{d{t}^2}=\frac{\beta }{m^2{r}^3}\end{array}}$

Hemos supuesto que β es constante y obtenemos de nuevo la ecuación del movimiento en la dirección radial

2. A partir de la segunda ecuación diferencial del movimiento en θ

${\displaystyle \begin{array}{l}m\frac{d}{dt}\left(r^2\frac{d\theta }{dt}\right)-m{\left(r\frac{d\phi }{dt}\right)}^2\sin \theta \cos \theta -\frac{qp}{4\pi {\epsilon }_0{r}^2}\sin \theta =0\\ m\frac{d}{dt}\left(r^2\frac{d\theta }{dt}\right)-\frac{L_z^2\cos \theta }{m{r}^2{\sin }^3\theta }-\frac{qp}{4\pi {\epsilon }_0{r}^2}\sin \theta =0\end{array}}$

Multiplicamos por $2m{r}^2\frac{d\theta }{dt}$

${\displaystyle \begin{array}{l}2m{r}^2\frac{d\theta }{dt}\frac{d}{dt}\left(r^2\frac{d\theta }{dt}\right)-2m{r}^2\frac{d\theta }{dt}\frac{L_z^2\cos \theta }{m{r}^2{\sin }^3\theta }-2m{r}^2\frac{d\theta }{dt}\frac{qp}{4\pi {\epsilon }_0{r}^2}\sin \theta =0\\ 4m{r}^3{\left(\frac{d\theta }{dt}\right)}^2\frac{dr}{dt}+2m{r}^4\frac{d\theta }{dt}\frac{d^2\theta }{d{t}^2}-2\frac{L_z^2\cos \theta }{{\sin }^3\theta }\frac{d\theta }{dt}-m\frac{qp}{2\pi {\epsilon }_0}\sin \theta \frac{d\theta }{dt}=0\end{array}}$

Comprobamos que esta expresión es la derivada dβ/dt

${\displaystyle \begin{array}{l}\beta =m^2{r}^4{\left(\frac{d\theta }{dt}\right)}^2+\frac{L_z^2}{{\sin }^2\theta }+m\frac{qp}{2\pi {\epsilon }_0}\cos \theta \\ \frac{d\beta }{dt}=4m^2{r}^3\frac{dr}{dt}{\left(\frac{d\theta }{dt}\right)}^2+2m^2{r}^4\left(\frac{d\theta }{dt}\right)\frac{d^2\theta }{dt}-2\frac{L_z^2}{{\sin }^3\theta }\cos \theta \frac{d\theta }{dt}-m\frac{qp}{2\pi {\epsilon }_0}\sin \theta \frac{d\theta }{dt}\end{array}}$

Como dβ/dt=0, β es una constante del movimiento

3. A partir de la ecuación del movimiento en la dirección radial

${\displaystyle \begin{array}{l}m\left(r\frac{d^{2}r}{d{t}^2}+{\left(\frac{dr}{dt}\right)}^2\right)=2E\\ r^2\frac{dr}{dt}\frac{d^{2}r}{d{t}^2}+r{\left(\frac{dr}{dt}\right)}^3=2\frac{E}{m}r\frac{dr}{dt}\\ \frac{d}{dt}\left(\frac{1}{2}{r}^2{\left(\frac{dr}{dt}\right)}^2-\frac{E}{m}{r}^2\right)=0\\ \frac{1}{2}{r}^2{\left(\frac{dr}{dt}\right)}^2-\frac{E}{m}{r}^2=C\\ E=\frac{1}{2}m{\left(\frac{dr}{dt}\right)}^2-\frac{mC}{r^2}\end{array}}$

Identificamos la constante C de integración con β en la conservación de la energía

Movimiento sobre una superficie esférica

En este apartado estudiamos el caso en el que la distancia de la partícula cargada al dipolo permanece constante. La partícula se mueve sobre una superficie esférica de radio r₀. Para ello, la energía de la partícula E=0 y también ${\left(\frac{dr}{dt}\right)}_0=0$, la posición inicial es de retorno

Se cumple además, que β=0

${\displaystyle \begin{array}{l}E=\frac{1}{2}m{\left(\frac{dr}{dt}\right)}_0^2+\frac{\beta }{2m{r}_0^2}\\ \beta =m^2{r}_0^4{\left(\frac{d\theta }{dt}\right)}^2+\frac{L_z^2}{{\sin }^2\theta }+m\frac{qp}{2\pi {\epsilon }_0}\cos \theta =0\end{array}}$

Dividiendo por $m{r}_0^2$

${\displaystyle \frac{1}{2}m{r}_0^2{\left(\frac{d\theta }{dt}\right)}^2+\frac{L_z^2}{2m{r}_0^2{\sin }^2\theta }+\frac{qp}{4\pi {\epsilon }_0{r}_0^2}\cos \theta =0}$

Cuando L_z=0, tenemos el ejemplo estudiado en el primer apartado de esta página

En el caso general, ésta es la ecuación del movimiento de una partícula en el potencial efectivo

${\displaystyle V_{ef}\left(\theta \right)=\frac{L_z^2}{2m{r}_0^2{\sin }^2\theta }+\frac{qp}{4\pi {\epsilon }_0{r}_0^2}\cos \theta }$

Representamos la función

${\displaystyle V_{ef}\left(\theta \right)=\frac{h}{{\sin }^2\theta }+k\cos \theta }$

h es positivo, pero k puede ser positivo o negativo dependiendo del signo de la carga q de la partícula. Mantenemos fijo h=1, y cambiamos k=3, 2, -2, -3

h=1;
hold on
k=3;
f=@(x) h./sin(x).^2+k*cos(x);
fplot(f,[pi/6,5*pi/6])

k=2;
f=@(x) h./sin(x).^2+k*cos(x);
fplot(f,[pi/6,5*pi/6])

k=-2;
f=@(x) h./sin(x).^2+k*cos(x);
fplot(f,[pi/6,5*pi/6])

k=-3;
f=@(x) h./sin(x).^2+k*cos(x);
fplot(f,[pi/6,5*pi/6])

line([pi/12,pi-pi/12],[0,0])
grid on
legend('3','2','-2','-3','location','best')
ylim([-1,8])
xlim([pi/6,5*pi/6])
set(gca,'XTick',pi/6:pi/6:5*pi/6)
set(gca,'XTickLabel',{'\pi/6','\pi/3','\pi/2','2\pi/3','5\pi/6'})
xlabel('\theta')
ylabel('V_e(\theta)')
title('Energía potencial efectiva')

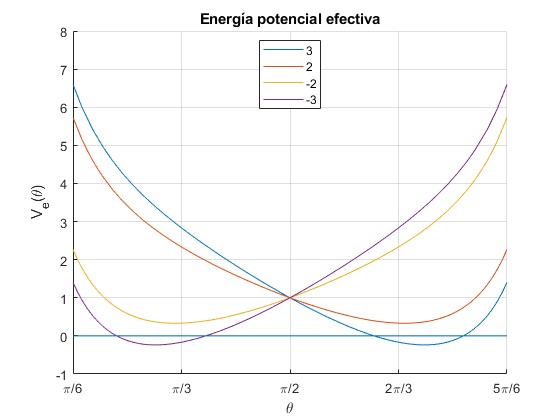
La energía potencial efectiva para k=2,-2, no cortan a la línea horizontal E=0. La energía potencial efectiva para k=3,-3, corta a la energía E=0 en dos puntos. La partícula se mueve entre dos posiciones angulares θ₁ y θ₂ en el hemisferio sur θ>π/2 si k es positivo y en el hemisferio norte θ<π/2 si k es negativo.

θ₁ y θ₂ son las raíces de la ecuación

${\displaystyle V_{ef}\left(\theta \right)=\frac{h}{{\sin }^2\theta }+k\cos \theta =0}$

Haciendo el cambio de variable

${\displaystyle \begin{array}{l}x=\cos \theta \\ \frac{h}{1-x^2}+kx=0\\ x^3-x-\frac{h}{k}=0\\ x^3-x-\frac{2\pi {\epsilon }_0{L}_z^2}{mqp}=0\end{array}}$

La ecuación cúbica x³+ax²+bx+c=0, tiene tres raíces reales si R²<Q³

${\displaystyle Q=\frac{a^2-3b}{9}R=\frac{2a^3-9ab+27c}{54}}$

En este caso, a=0, b=-1 y c=-h/k, por tanto, Q=1/3 y R=-h/(2k)

${\displaystyle \begin{array}{l}{R}^2<Q^3\\ \frac{h^2}{4k^2}<\frac{1}{27}\\ 27h^2<4k^2\\ k>\frac{3\sqrt{3}}{2}h,\frac{qp}{4\pi {\epsilon }_0{r}_0^2}>\frac{3\sqrt{3}}{2}\frac{L_z^2}{2m{r}_0^2},L_z^2<\frac{mqp}{3\sqrt{3}\pi {\epsilon }_0}\end{array}}$

Para h=1 y k=3, R=-1/6, se cumple que 1/36<1/27 por tanto, tiene tres raíces reales que se calculan mediante la fórmula

${\displaystyle \theta =\arccos \left(\frac{R}{\sqrt{Q^3}}\right)\{\begin{array}{l}{x}_1=-2\sqrt{Q}\cos \left(\frac{\theta }{3}\right)-\frac{a}{3}\\ x_2=-2\sqrt{Q}\cos \left(\frac{\theta +2\pi }{3}\right)-\frac{a}{3}\\ x_3=-2\sqrt{Q}\cos \left(\frac{\theta -2\pi }{3}\right)-\frac{a}{3}\end{array}}$

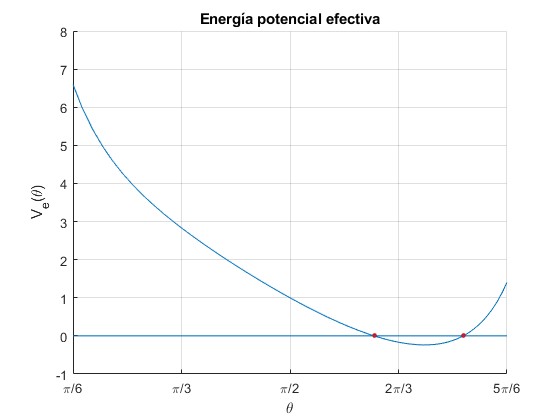
Se calculan y se señalan mediante puntos de color rojo, los ángulos θ₁ y θ₂

h=1;
hold on
k=3;
f=@(x) h./sin(x).^2+k*cos(x);
fplot(f,[pi/6,5*pi/6])
R=-h/(2*k);
Q=1/3;
th=acos(R/sqrt(Q^3));
x_1=-2*sqrt(Q)*cos(th/3);
x_2=-2*sqrt(Q)*cos((th+2*pi)/3);
x_3=-2*sqrt(Q)*cos((th-2*pi)/3);
th_1=acos(x_1);
th_2=acos(x_3);
plot(th_1,0,'ro','markersize',3,'markerfacecolor','r')
plot(th_2,0,'ro','markersize',3,'markerfacecolor','r')

line([pi/12,pi-pi/12],[0,0])
grid on
ylim([-1,8])
xlim([pi/6,5*pi/6])
set(gca,'XTick',pi/6:pi/6:5*pi/6)
set(gca,'XTickLabel',{'\pi/6','\pi/3','\pi/2','2\pi/3','5\pi/6'})
xlabel('\theta')
ylabel('V_e(\theta)')
title('Energía potencial efectiva')

De las tres raíces reales de la ecuación cúbica en x=cosθ, se descarta la segunda, que es mayor que la unidad en valor absoluto

>> x_1,x_2,x_3
x_1 =   -0.7422
x_2 =    1.1372
x_3 =   -0.3949

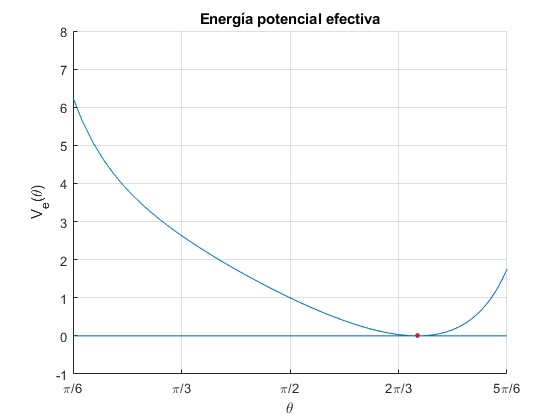
Cuando el mínimo de la energía potencial efectiva es nulo, solamente hay un ángulo θ₀

Esta situación se produce cuando R²=Q³

${\displaystyle \begin{array}{l}{R}^2=Q^3\\ {\left(-\frac{h}{2k}\right)}^2={\left(\frac{1}{3}\right)}^3\\ k=\frac{3\sqrt{3}}{2}h,\frac{qp}{4\pi {\epsilon }_0{r}_0^2}=\frac{3\sqrt{3}}{2}\frac{L_z^2}{2m{r}_0^2},L_z^2=\frac{mqp}{3\sqrt{3}\pi {\epsilon }_0}\end{array}}$

Para h=1, la raíz es $x_1=-\frac{1}{\sqrt{3}}$, θ₀=arccos(x₁)

Se señala mediante un punto de color rojo, el ángulo θ₀ tangente a la línea horizontal E=0

h=1;
hold on
k=3*sqrt(3)*h/2;
f=@(x) h./sin(x).^2+k*cos(x);
fplot(f,[pi/6,5*pi/6])
R=-h/(2*k);
Q=1/3;
th=acos(R/sqrt(Q^3));
x_1=-2*sqrt(Q)*cos(th/3);
x_2=-2*sqrt(Q)*cos((th+2*pi)/3);
x_3=-2*sqrt(Q)*cos((th-2*pi)/3);
th_0=acos(x_1);
plot(th_0,0,'ro','markersize',3,'markerfacecolor','r')

line([pi/12,pi-pi/12],[0,0])
grid on
ylim([-1,8])
xlim([pi/6,5*pi/6])
set(gca,'XTick',pi/6:pi/6:5*pi/6)
set(gca,'XTickLabel',{'\pi/6','\pi/3','\pi/2','2\pi/3','5\pi/6'})
xlabel('\theta')
ylabel('V_e(\theta)')
title('Energía potencial efectiva')

De las tres raíces reales de la ecuación cúbica en x=cosθ, dos son iguales y se descarta la segunda, que es mayor que la unidad en valor absoluto

>> x_1,x_2,x_3
x_1 =   -0.5774 - 0.0000i
x_2 =    1.1547 - 0.0000i
x_3 =   -0.5774 + 0.0000i

Referencias

George C. McGuire. Using computer algebra to investigate the motion of an electric charge in magnetic and electric dipole fields. Am. J. Phys. 71(8), August 2003, pp. 809-812

Victor Varela, Rita Gianvittorio. Unstable motion of a point charge near an electric dipole. Eur. J. Phys. 46 (2025) 035003

Sergio Gutiérrez-López, Arnulfo Castellanos-Moreno, Rodrigo Arturo Rosas-Burgos. A new constant of motion for an electric charge acted on by a point electric dipole. Am. J. Phys. 76 (12), December 2008, pp. 1141-1145