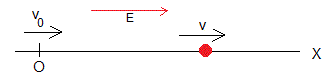
Aplicamos un campo eléctrico oscilante a un haz de partículas de msas m y carga q

${\displaystyle E=E_0\sin \left(\omega t+\phi \right)}$

a lo largo del eje X, en la dirección de la velocidad de la partícula. La ecuación del movimiento es

${\displaystyle \begin{array}{l}m\frac{dv}{dt}=q{E}_0\sin \left(\omega t+\phi \right)\\ {\displaystyle \underset{v_0}{\overset{v}{\int }}dv}=\frac{q{E}_0}{m}{\displaystyle \underset{0}{\overset{t}{\int }}\sin \left(\omega t+\phi \right)dt}\\ v=v_0+\frac{q{E}_0}{m\omega }\left\{-\cos \left(\omega t+\phi \right)+\cos \phi \right\}\end{array}}$

Integrando, de nuevo

${\displaystyle \begin{array}{l}\frac{dx}{dt}=v_0+\frac{q{E}_0}{m\omega }\left\{\cos \phi -\cos \left(\omega t+\phi \right)\right\}\\ {\displaystyle \underset{0}{\overset{x}{\int }}dx}={\displaystyle \underset{0}{\overset{t}{\int }}\left(v_0+\frac{q{E}_0}{m\omega }\left\{\cos \phi -\cos \left(\omega t+\phi \right)\right\}\right)dt}\\ x=v_{0}t+\frac{q{E}_0}{m\omega }\left\{\cos \phi ·t-\frac{1}{\omega }\left(\sin \left(\omega t+\phi \right)+\sin \phi \right)\right\}\\ x=\left(v_0+\frac{q{E}_0}{m\omega }\cos \phi \right)t+\frac{q{E}_0}{m{\omega }^2}\left\{\sin \phi -\sin \left(\omega t+\phi \right)\right\}\end{array}}$

El movimiento de la partícula consiste en una combinación de un desplazamiento (primer término proporcional a t) y una oscilación (segundo término). El primer término hace que la partícula se mueva a lo largo del eje X, alejándose del origen. El segundo término, hace que la partícula permenezca confinada oscilando alrededor de una posición media

Vamos a analizar los distntos casos

• La partícula en el instante inicial t=0, parte del reposo, v₀=0

Cuando la fase φ=π/2 o 3π/2, la partícula permanecerá confinada oscilando (segundo término) bajo la acción de un campo eléctrico ±E₀cos(ωt) independientemente de su relación q/m

• La partícula en el instante inicial t=0, su velocidad es v₀

Si elegimos la fase de modo que el primer término sea nulo, entonces la partícula permanecerá confinada oscilando

${\displaystyle v_0+\frac{q{E}_0}{m\omega }\cos \phi =0}$

El valor medio de una función periódica f(t) de periodo P es

${\displaystyle \langle f(t)\rangle =\frac{1}{P}{\displaystyle \underset{0}{\overset{P}{\int }}f(t)·dt}}$

Cuando la partícula oscila, la posición media es

${\displaystyle \begin{array}{l}{x}_m=\frac{1}{\frac{2\pi }{\omega }}{\displaystyle \underset{0}{\overset{2\pi /\omega }{\int }}\left(\frac{q{E}_0}{m{\omega }^2}\left\{\sin \phi -\sin \left(\omega t+\phi \right)\right\}\right)dt}\\ =\frac{\omega }{2\pi }\frac{q{E}_0}{m{\omega }^2}\left(\sin \phi \frac{2\pi }{\omega }+\frac{1}{\omega }\left(\cos \left(2\pi +\phi \right)-\cos \phi \right)\right)=\frac{q{E}_0}{m{\omega }^2}\sin \phi \end{array}}$

En términos de magnitudes adimensionales

${\displaystyle \begin{array}{l}\xi =\frac{m{\omega }^2}{q{E}_0}x,\tau =\omega t\\ \frac{m{\omega }^2}{q{E}_0}x=\left(\frac{m{\omega }^2}{q{E}_0}{v}_0+\frac{m{\omega }^2}{q{E}_0}\frac{q{E}_0}{m\omega }\cos \phi \right)\frac{\tau }{\omega }+\frac{m{\omega }^2}{q{E}_0}\frac{q{E}_0}{m{\omega }^2}\left\{\sin \phi -\sin \left(\tau +\phi \right)\right\}\\ \xi =\left(\frac{m\omega }{q{E}_0}{v}_0+\cos \phi \right)\tau +\sin \phi -\sin \left(\tau +\phi \right)\\ \xi =\left(V_0+\cos \phi \right)\tau +\sin \phi -\sin \left(\tau +\phi \right)\end{array}}$

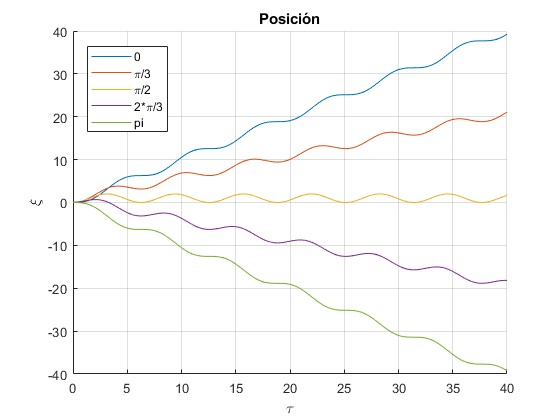
Representamos la posición ξ en función del tiempo τ para una partícula cargada que parte del reposo V₀=0 que se mueve a lo largo del eje X bajo la acción de un campo eléctrico oscilante, las fase son φ=0, π/3, π/2, 2*π/3, π

hold on
for phi=[0,pi/3,pi/2,2*pi/3,pi]
    f=@(t) cos(phi)*t+sin(phi)-sin(t+phi);
    fplot(f,[0,40])
end
hold off
grid on
xlabel('\tau')
legend('0','\pi/3','\pi/2','2*\pi/3','pi','location','best')
ylabel('\xi')
title('Posición')

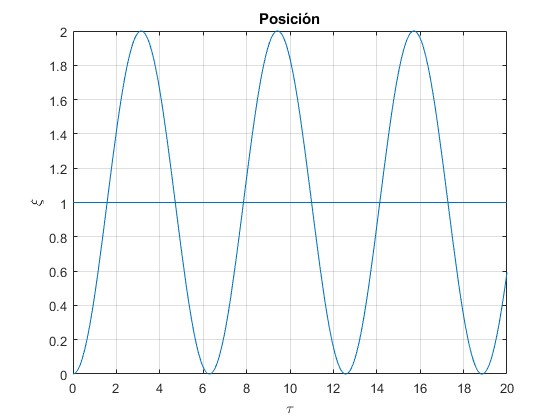
Como apreciamos para φ=π/2, la partícula permenecerá confinada oscilando, alrededor de la posición media x_m=sinφ=1, independientemente de su relación q/m

phi=pi/2;
f=@(t) sin(phi)-sin(t+phi);
fplot(f,[0,20])
line([0,20],[sin(phi),sin(phi)])
grid on
xlabel('\tau')
ylabel('\xi')
title('Posición')

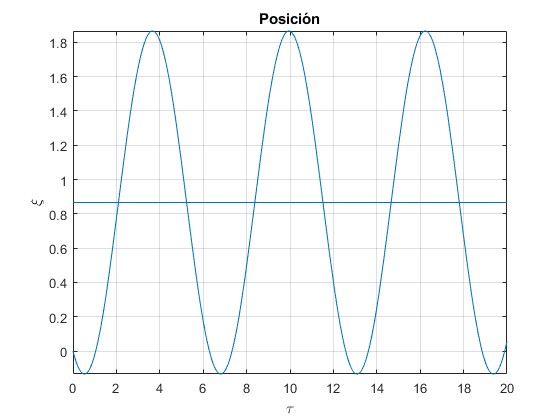
Supongamos una partícula cuya V₀≤1 no nula. Si la fase del campo es tal que cosφ=-V₀, entonces la partícula permanecerá confinada

V0=0.5;
phi=acos(-V0);
f=@(t) sin(phi)-sin(t+phi);
fplot(f,[0,20])
line([0,20],[sin(phi),sin(phi)])
grid on
xlabel('\tau')
ylabel('\xi')
title('Posición')

La partícula cargada oscila alrededor de la posición ${\xi }_m=\frac{\sqrt{3}}{2}$, tal como se muestra en la figura

La aplicación práctica es la separación de iones de distinto q/m o la determinación de su relación q/m.

Separación de iones de distinta relación q/m

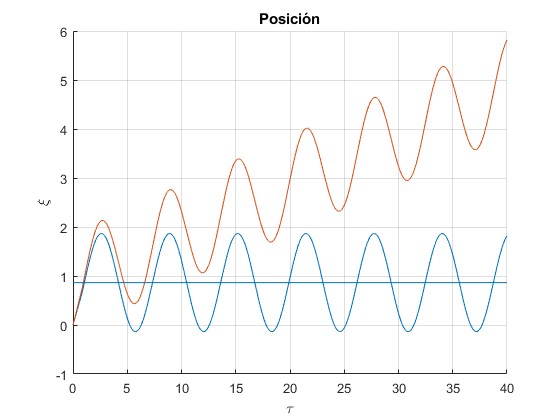
Spongamos que utilizamos una mezcla de iones provenientes de un selector de velocidades, la velocidad de los iones es v₀=E/B

Seleccionamos la fase φ de modo que los iones de relación (q/m)₁ permenezcan confinados

${\displaystyle v_0+{\left(\frac{q}{m}\right)}_1\frac{E_0}{\omega }\cos \phi =0}$

Entonces los iones de relación (q/m)₂ continuarán moviendose lo largo de eje X oscilando

V0=0.5;
phi=acos(-V0);
hold on
f=@(t) sin(phi)-sin(t+phi); %confinados
fplot(f,[0,40])
V0=0.6;
f=@(t) (V0+cos(phi))*t+sin(phi)-sin(t+phi); %desplazan
fplot(f,[0,40])
line([0,40],[sin(phi),sin(phi)])
grid on
xlabel('\tau')
ylabel('\xi')
title('Posición')

Relación q/m

Conocida la fase φ del campo eléctrico, para que los iones del mismo tipo permanezcan confinados oscilando alrededor de la posición x_m, despejamos la relación q/m

${\displaystyle \frac{q}{m}=-\frac{v_0\omega }{E_0\cos \phi }}$

Es posible que los iones en vez de provenir de un selector de velocidades, hayan sido acelerados por una diferencia de potencial V_a, entonces la velocidad v₀ de los iones es

${\displaystyle \begin{array}{l}\frac{1}{2}m{v}_0^2=q{V}_a\\ v_0=\sqrt{2V_a}\sqrt{\frac{q}{m}}\\ \frac{q}{m}=-\frac{\omega }{E_0\cos \phi }\sqrt{2V_a}\sqrt{\frac{q}{m}}\\ \frac{q}{m}=\frac{2V_a{\omega }^2}{E_0^2{\cos }^2\phi }\end{array}}$

De esta última expresión, calculamos la relación q/m de los iones

Referencias

Pirooz Mohazzabi, Ben Greenebaum. Phase-sensitive particle separation using alternating longitudinal electric field. Can. J. Phys. 88: 271–275 (2010)